2021—2022学年北师大版数学九年级上册第四章图形的相似难点突破证明题存在性问题专练1(word版含解析)
文档属性
| 名称 | 2021—2022学年北师大版数学九年级上册第四章图形的相似难点突破证明题存在性问题专练1(word版含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 407.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-03 00:00:00 | ||
图片预览



文档简介
北师大版数学九年级上期第四章图形的相似
证明题存在性问题专练1(难点突破)
如图,正方形ABCD的边长为2, E是CD中点, 点P在射线AB上,过点P作线段AE的垂线段, 垂足为F.
(1)求证:△PAF∽△AED;
(2)连接PE, 若存在点P使△PEF与△AED相似,直接写出PA的长.
如图1,在平行四边形ABCD中,AB=3cm,BC=5cm,AC⊥AB,△ACD沿AC的方向匀速平移得到△PNM,速度为1cm/s;同时点Q从点C出发,沿着CB方向匀速移动,速度为1cm/s;当△PNM停止移动时,点Q也停止移动,如图2,设移动时间为ts(0<t<4).连接PQ,MQ,MC.解答下列问题.
(1)当t为何值时,PQ∥MN?
(2)是否存在某一时刻t,使PQ⊥MQ?若存在,求出t的值;若不存在,请说明理由.
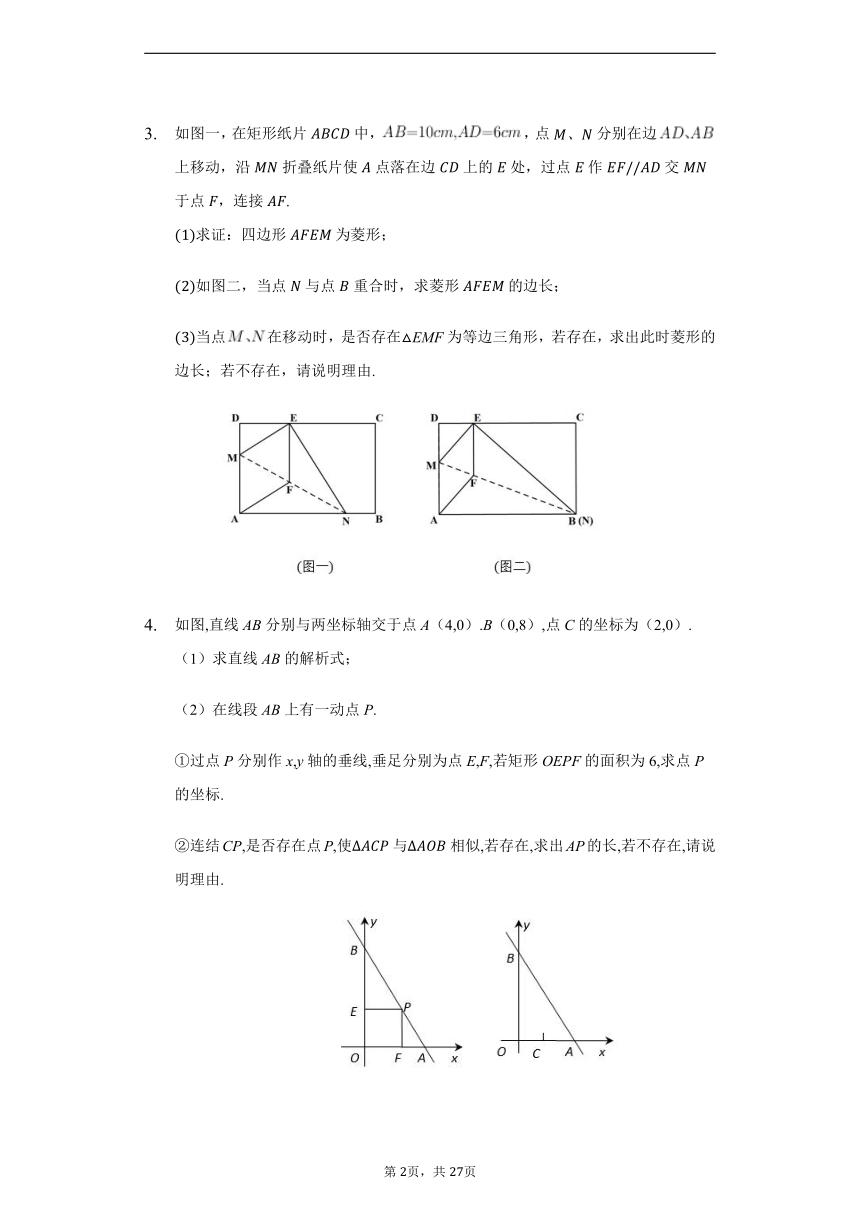
如图一,在矩形纸片中,,点分别在边上移动,沿折叠纸片使点落在边上的处,过点作交于点,连接.
求证:四边形为菱形;
如图二,当点与点重合时,求菱形的边长;
当点在移动时,是否存在EMF为等边三角形,若存在,求出此时菱形的边长;若不存在,请说明理由.
如图,直线AB分别与两坐标轴交于点A(4,0).B(0,8),点C的坐标为(2,0).
(1)求直线AB的解析式;
(2)在线段AB上有一动点P.
①过点P分别作x,y轴的垂线,垂足分别为点E,F,若矩形OEPF的面积为6,求点P的坐标.
②连结CP,是否存在点P,使与相似,若存在,求出AP的长,若不存在,请说明理由.
如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD⊥AB于点D.点P从点D出发,沿线段DC向点C运动,点Q从点C出发,沿线段CA向点A运动.两点同时出发.速度都为每秒1个单位长度,当点P运动到C时,两点都停止.设运动时间为t秒.
(1)求线段CD的长;
(2)设△CPQ的面积为S,求S与t之间的函数关系式,并确定在运动过程中是否存在某一时刻t,使得S△CPQ:S△ABC=9:100?若存在,求出t的值;若不存在,说明理由.
如图,在Rt△ABC中,∠B=90°,AB=3cm,BC=4cm.点P从点A出发,以1cm/s的速度沿AB运动;同时,点Q从点B出发,以2cm/s的速度沿BC运动.当点Q到达点C时,P、Q两点同时停止运动.
(1)当运动时间t为何值时,以P、B、Q为顶点的三角形与△ABC相似
(2)是否存在某一时刻t,△PBQ的面积恰为3cm2 若存在,求出运动时间t;若不存在,请说明理由.
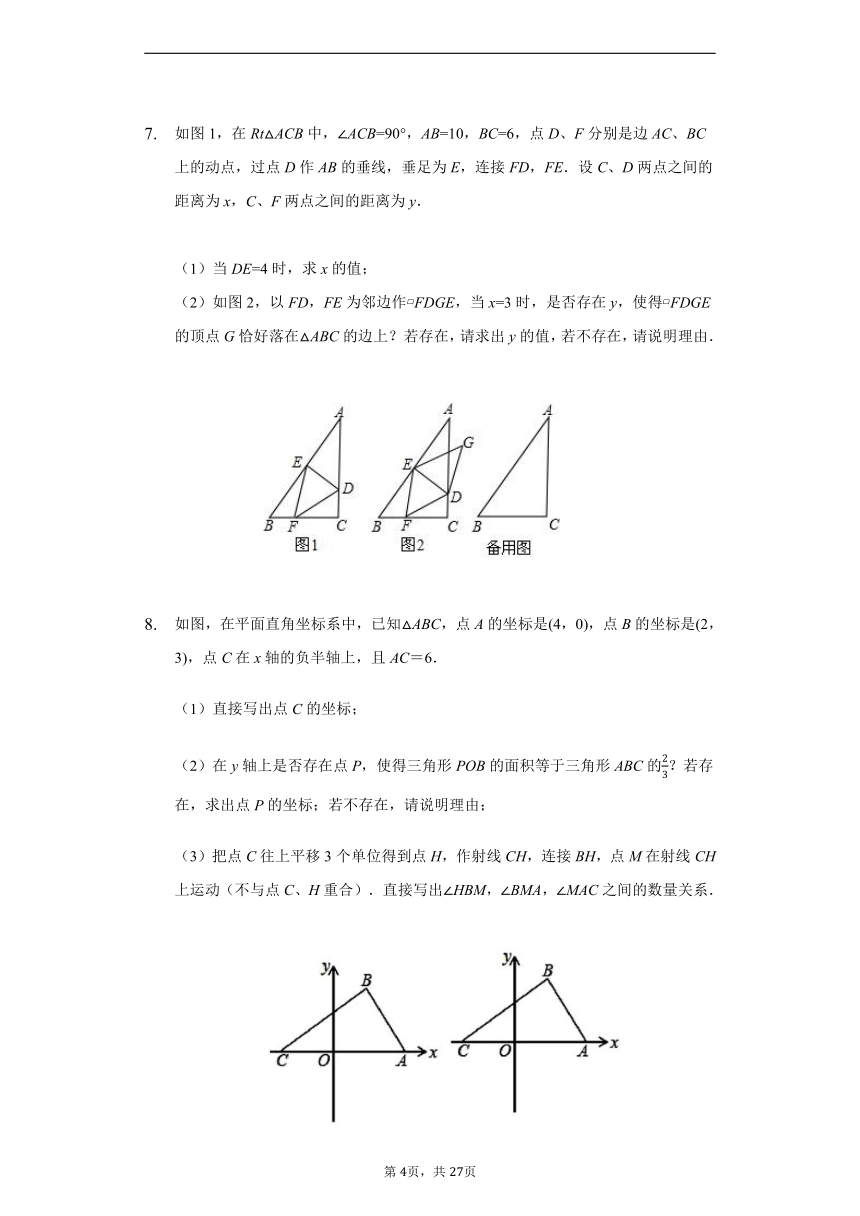
如图1,在Rt△ACB中,∠ACB=90°,AB=10,BC=6,点D、F分别是边AC、BC上的动点,过点D作AB的垂线,垂足为E,连接FD,FE.设C、D两点之间的距离为x,C、F两点之间的距离为y.
(1)当DE=4时,求x的值;
(2)如图2,以FD,FE为邻边作 FDGE,当x=3时,是否存在y,使得 FDGE的顶点G恰好落在△ABC的边上?若存在,请求出y的值,若不存在,请说明理由.
如图,在平面直角坐标系中,已知△ABC,点A的坐标是(4,0),点B的坐标是(2,3),点C在x轴的负半轴上,且AC=6.
(1)直接写出点C的坐标;
(2)在y轴上是否存在点P,使得三角形POB的面积等于三角形ABC的?若存在,求出点P的坐标;若不存在,请说明理由;
(3)把点C往上平移3个单位得到点H,作射线CH,连接BH,点M在射线CH上运动(不与点C、H重合).直接写出∠HBM,∠BMA,∠MAC之间的数量关系.
如图,已知矩形ABCD中,AB=10cm,BC=20cm,两只蚂蚁P和Q同时分别从A、B出发,沿AB、BC向B、C方向前进,P蚂蚁每秒钟走1cm,Q蚂蚁每秒钟的速度是P蚂蚁的速度的2倍,结果同时到达B和C点,
(1)都爬行4秒钟后,两蚂蚁的最短距离PQ长是多少cm?
(2)两蚂蚁同时出发t秒钟后,以P、B、Q为顶点的三角形与以A、B、D为顶点的三角形相似,求t的值;
(3)是否存在这样的t(秒)值,使PQ// AC?若存在,求出t的值,若不存在,请说明理由.
如图,在平面直角坐标系中,已知△ABC,点A的坐标是(4,0),点B的坐标是(2,3),点C在x轴的负半轴上,且AC=6.
(1)直接写出点C的坐标;
(2)在y轴上是否存在点P,使得S△POB=S△ABC若存在,求出点P的坐标;若不存在,请说明理由;
(3)把点C往上平移3个单位得到点H,作射线CH,连接BH,点M在射线CH上运动(不与点C、H重合).试探究∠HBM,∠BMA,∠MAC之间的数量关系,并证明你的结论.
如图,直线AB分别与两坐标轴交于点A(4,0).B(0,8),点C的坐标为(2,0).
(1)求直线AB的解析式;
(2)在线段AB上有一动点P.
①过点P分别作x,y轴的垂线,垂足分别为点E,F,若矩形OEPF的面积为6,求点P的坐标.
②连结CP,是否存在点P,使与相似,若存在,求出点P的坐标,若不存在,请说明理由.
如图,在等腰Rt△ABC中,∠ACB=90°,AB=,点D,E分别在边AB,BC上,将线段ED绕点E按逆时针方向旋转90°得到EF。
(1)如图①,若AD=BD,点E与点C重合,AF与DC相交于点O。
求证:BD=2DO;
(2)已知点G为AF的中点。
①如图②,若AD=BD,CE=2,求DG的长;
②若AD=6BD,是否存在点E,使得△DEG是直角三角形?若存在,求CE的长;若不存在,试说明理由。
如图1,已知点A(x1,0),B(x2,0),其中x1,x2是方程x2-8x+12=0的两根,且x1<x2,C(3,).
(1)求点A、B的坐标.
(2)作CH⊥AB于H,设E为OC延长线上一点,连EH交线段BC于F,问是否存在点E,使△CHF与△BEF相似?如果存在,求OE的长,如果不存在,说明理由.
(3)如图2,取AB的中点D,问在直线CD上是否存在点P,使△ABP是直角三角形?若存在,求出所有符合条件的P点的坐标;若不存在,请说明理由.
如图,正方形ABCD的边长为4,E是CD中点,点P在射线AB上,过点P作线段AE的垂线段,垂足为F.
(1)求证:△PAF∽△AED;
(2)连接PE,若存在点P使△PEF与△AED相似,直接写出PA的长______.
如图,在Rt△ABC 中,AC=4cm , BC=3cm,点P由B出发沿BA的方向向点A匀速运动,速度为1 cm /s,同时点Q由 A出发沿AC的方向向点C匀速运动,速度为1cm /s,连接PQ,设运动的时间为t(s),其中0<t<4,解答下列问题:
(1)当t为何值时,以P、Q、A为顶点的三角形与△ABC相似?
(2)点P、Q在运动过程中,△CPQ能否成为等腰三角形?若能,请求出此时t的值,若不存在,请说明理由.
如图所示,在等腰△ABC中,AB=AC=10cm,BC=16cm.点D由点A出发沿AB方向向点B匀速运动,同时点E由点B出发沿BC方向向点C匀速运动,它们的速度均为1cm/s.连接DE,设运动时间为t(s)(0<t<10),解答下列问题:
(1)当t为何值时,△BDE的面积为7.5cm2;
(2)在点D,E的运动中,是否存在时间t,使得△BDE与△ABC相似?若存在,请求出对应的时间t;若不存在,请说明理由.
参考答案
1.(1)证明:∵正方形ABCD,
∴CD∥AB,∠D=90°
∴∠AED=∠PAF,
又∵PF⊥AE,
∴∠PFA=∠D=90°.
∴△PFA∽△ADE.
(2)情况1,当△EFP∽△ADE,且∠PEF=∠EAD时,
则有PE∥AD
∴四边形ADEP为矩形.
∴PA=ED=1;
情况2,当△PFE∽△ADE,且∠PEF=∠AED时,
∵∠PAF=∠AED,
∴∠PEF=∠PAF.
∴PE=PA.
∵PF⊥AE,
∴点F为AE的中点.
∵AE==,
∴AF=,
∵△PFA∽△ADE,
=,
∴=,
∴PA=
∴满足条件的PA的值为1或.
2.解:(1)在Rt△ABC中,,
由平移的性质得MN∥AB,
∵PQ∥MN,
∴PQ∥AB,
∴,
∴,
解得;
(2)若PQ⊥MQ,
则∠PQM=∠PEQ,
∵∠MPQ=∠PQE,
∴△PEQ∽△MQP,
∴,
∴PQ2=MP EQ,
∴PE2+EQ2=MP EQ,
∵,
∴,
∴,
∴t1=0(舍去),,
∴时,PQ⊥MQ.
3.解:(1)证明:∵折叠纸片使A点落在边AD上的E处,折痕为MN
∴点A与点E关于MN对称
∴AM=EM,AF=EF,∠AMF=∠EMF
又∵EF∥AD
∴∠AMF=∠EFM
∴∠EMF=∠EFM
∴ME=EF
∴AM=MF=EF=AF
∴四边形AMEF为菱形;
(2)当点与点重合时
∵四边形ABCD是矩形
∴BC=AD=6cm,CD=AB=10cm,∠BAD=∠D=90°
∵点A与点E关于MN对称
∴BE=AB=10cm
在Rt△BCE中,
∴DE=CD-CE=2cm
在Rt△MDE中,ME=AM=6-DM
∴ME2=DE2+DM2
即:
解得:
∴菱形BFEP的边长为cm;
(3)存在,理由如下:
当EMF为等边三角形时
又∵在△MEN中,MN=2ME
∴
解得:ME=4cm
当菱形的边长为4cm时,EMF为等边三角形
4.解:(1)设直线AB的解析式为y=kx+b,
∵A(4,0),B(0,8),
∴,
∴,
∴y=-2x+8;
(2)①设点P (x,-2x+8),则PE=x,PF=-2x+8,
∴S OEPF=PE PF=x(-2x+8)=6,
∴x1=1,x2=3;
经检验x1=1,x2=3都符合题意,
∴点P(1,6)或(3,2);
②∵△ACP和△AOB中,∠BAO=∠BAO,
∴只有以下两种情况,
当△ACP∽△AOB时,
∵A(4,0),B(0,8),C(2,0),
∴OA=4,OB=8,OC=2,
∴AC=OC=2,
在△AOB中,∠AOB=90°,
∴AB2=OA2+OB2,
即AB2=42+82,
∴AB=(负值舍去),
∵△ACP∽△AOB,
∴,
即,
解得:AP=;
当△APC∽△AOB时,
∴,
即,
解得:,
综上所述,当AP=或时,△ACP与△AOB相似.
5.解:(1)∵∠ACB=90°,AC=8,BC=6,
∴AB===10,
∵AC BC=AB CD,
∴×8×6=×10CD,
解得:CD=4.8;
(2)AD===6.4,
过点Q作QH⊥CD于H,如图所示:
∵CD⊥AB,
∴QH∥AD,
∴△CHQ∽△CDA,
∴=,即=,
∴QH=0.8t,
∴S=QH CP=×0.8t×(4.8-t)=-0.4t2+1.92t;
∵S△ABC=AC BC=×8×6=24,
S△CPQ:S△ABC=9:100,即:=,
整理得:5t2-24t+27=0,
解得:t1=3,t2=1.8,
∴在运动过程中存在某一时刻t,使得S△CPQ:S△ABC=9:100,t的值为:3或1.8.
6.解:(1)由题意得,t秒时,PB=(3-t)cm,BQ=2tcm,
①当△PBQ∽△ABC时,则,
即,
解得t=;
②当△QBP∽△ABC时,则,
即,
解得.
综上,当t=s或s时,△PBQ与△ABC相似;
(2)设经过t秒,△PBQ的面积等于3cm2.
∵,
∴-t2+3t-3=0,
∵△=b2-4ac=32-4(-1)(-3)=9-12=-3<0,
∴此方程无解,
故不存在某一时刻t,△PBQ的面积恰为3cm2.
7.解:(1)∵DE⊥AB,AC⊥BC,
∴∠AED=∠C=90°.
∵∠A=∠A,
∴△ADE∽△ABC.
∴.
∴,
∴AD=.
在Rt△ABC中,
∵∠ACB=90°,AB=10,BC=6,
∴AC==8.
∴CD=AC-AD=8-=.
∴.
(2)存在,理由:
①如下图,G落在AC上,
∵EF∥AC,
∴△EBF∽△ABC,
∴.
设BF=3k,EB=5k,
∴AE=10-5k,
∵DC=3,
∴AD=8-3=5.
由(1)知:△ADE∽△ABC,
∴.
∴AE=4,
∴10-5k=4,
∴,
∴,
∴.
②如下图,G落在AB上,
∵DF∥AB,
∴△DFC∽△ABC,
∴.
∴
∴y=.
综上,当x=3时,存在y=或.,使得 FDGE的顶点G恰好落在△ABC的边上.
8.解:(1)∵A(4,0),
∴OA=4,
∵AC=6,
∴OC=2,
∴C(-2,0);
(2)在y轴上存在点P,使得三角形POB的面积等于三角形ABC的,
设P(0,m),
由题意: |m| 2=××6×3,
解得,
m=±6,
∴P(0,6)或(0,-6);
(3)①当点M在点H的上方时,∠MAC=∠AMB+∠HBM,
理由:设AM交BH于J,
∵BH∥AC,
∴∠CAM=∠HJM,
∵∠HJM=∠AMB+∠HBM,
∴∠MAC=∠AMB+∠HBM,
②当点M在线段CH上(不与C,H重合)时,
∠AMB=∠CAM+∠HBM,
理由:作MK∥HB,
∵HB∥AC,
∴MK∥AC,
∴∠HBM=∠BMK,
∠CAM=∠KMA,
∴∠AMB=∠BMK+∠AMK=∠CAM+∠HBM.
9.解:(1)∵两只蚂蚁P和Q同时分别从A,B出发,沿AB,BC向B,C方形前进,蚂蚁P每秒走1cm,蚂蚁Q每秒走2cm,
∴都爬行4秒后,AP=4cm,BQ=8cm,
则BP=6cm,故PQ==10(cm),
则都爬行4秒后,两蚂蚁的最短距离PQ是10cm;
(2)设t秒时,由题意可得:BP=(10-t)cm,BQ=2tcm,
∠PBQ=∠ADC=90°,则需分下列两种情况讨论:
①当△ PBQ∽△BAD时,
则=,
即=,
解得:t=5,
②当△ QBP∽△BAD时,
则=,
即=,
解得:t=2,
综上,以P,B,Q为顶点的三角形与以A,B,D为顶点的三角形相似时,t=2s或5s.
(3)若PQ//AC,
则△PBQ∽△ABC,
∴=,
∴=,
解得t=5,
∴存在这样的t(秒)值,使PQ // AC,
此时t=5秒.
10.解:(1)∵A(4,0),
∴OA=4,
∵AC=6,
∴OC=2,
∴C(-2,0).
(2)设P(0,m),
由题意: |m| 2=××6×3,
解得m=±6,
∴P(0,6)或(0,-6).
(3)①当点M在点H的上方时,∠MAC=∠AMB+∠HBM.
理由:设AM交BH于J.
∵BH∥AC,
∴∠CAM=∠HJM,
∵∠HJM=∠AMB+∠HBM,
∴∠MAC=∠AMB+∠HBM.
②当点M在线段CH上(不与C,H重合)时,∠AMB=∠CAM+∠HBM.
理由:作MK∥HB.
∵HB∥AC,
∴MK∥AC,
∴∠HBM=∠BMK,∠CAM=∠KMA,
∴∠AMB=∠BMK+∠AMK=∠CAM+∠HBM.
11.解:(1)设直线AB的解析式为y=kx+b,
依题意,,
∴,
∴y=-2x+8;
(2)①设动点P (x,-2x+8),
则PE=x,PF=-2x+8,
∴S OEPF=PE PF=x(-2x+8)=6
∴x1=1,x2=3;
经检验x1=1,x2=3都符合题意,
∴点P(1,6)或(3,2);
②存在,分两种情况
第一种:CP∥OB,
∴△ACP∽△AOB,
而点C的坐标为(2,0),
∴点P(2,4 );
第二种CP⊥AB,
∵∠APC=∠AOB=90°,∠PAC=∠BAO,
∴△APC∽△AOB,
∴,
∴,
∴AP=,
如图,过点P作PH⊥x轴,垂足为H,
∴PH∥OB,
∴△APH∽△ABO,
∴,
∴,
∴PH=,
∴,
∴点P().
∴点P的坐标为(2,4)或点P().
12.解:(1)由旋转的性质得:CD=CF,∠DCF=90°
∵△ABC是等腰直角三角形,AD=BD
∴∠ADO=90°,CD=BD=AD
∴∠DCF=∠ADC
在△ADO和△FCO中,
∴△ADO≌△FCO(AAS)
∴DO=CO
∴BD=CD=2DO
(2)①如图,分别过点D,F作DN⊥BC于点N,FM⊥BC于点M,连结BF
∴∠DNE=∠EMF=90°
又∵NDE=∠MEF,DE=EF
∴△DNE≌△EMF(AAS)
∴DN=EM
又∵,∠ABC=45°
∴DN=EM=7
∴BM=BC-ME-EC=5
∴MF=NE=NC-EC=5
∴
∵点D,G分别是AB,AF的中点
∴
②过点D作DH⊥BC于点H
∵AD=6BD,
∴
(ⅰ)当∠DEG=90°时,有如图②,③两种情况,设CE=t
∵∠DEF=90°,∠DEG=90°
∴点E在线段AF上
∴BH=DH=2,BE=14-t,HE=BE-BH=12-t
∵△DHE∽△ECA
∴,即,解得
∴或
(ⅱ)当DG∥BC时,如图④,过点F作FK⊥BC于点K,延长DG交AC于点N,延长AC并截取MN=NA,连结FM,则NC=DH=2,MC=10
设GN=t,则FM=2t,BK=14-2t
∵△DHE△EKF
∴DH=EK=2,HE=KF=14-2t
∵MC=FK
∴14-2t=10
解得t=2
∵GN=EC=2,GN∥EC
∴四边形GECN为平行四边形,∠ACB=90°
∴四边形GECN为矩形
∴∠EGN=90°
∴当EC=2时,有∠DGE=90°
(ⅲ)当∠EDG=90°时,如图⑤,过点G,F分别作AC的垂线交射线于点N,M,过点F作FK⊥BC于点K,过点D作GN的垂线交NG的延长线于点P,则PN=HC=BC-HB=12
设GN=t,则FM=2t
∴PG=PN-GN=12-t
∵△DHE△EKF
∴EK=DH=2
∴CE=CK-KE=2t-2
∴HE=HC-CE=12-(2t-2)=14-2t
∴FK=HE=14-2t,AM=AC+CM=AC+FK=14+14-2t=28-2t
∴,NC=MN-CM=t
∴PD=t-2
∵△GPD∽△DHE
∴,即
解得,(舍去)
∴
综上所述,CE的长为、或.
13.解:(1)∵x1,x2是方程x2-8x+12=0的两根,
∴x1=2,x2=6,∴A(2,0),B(6,0);
(2)存在,理由:如图1,由(1)知,B(6,0),
∵CH⊥AB于H且C(3,),
∴H(3,0),
∴OH=BH=3,
∵CH=,在Rt△BCH中,tan∠CBH=,
∴∠CBH=30°,
∴∠BCH=60°,
∵点E在OC延长线上,
∴∠CHF<90°,
∵△CHF与△BEF相似,
∴△CHF∽△HBF,
∴∠BHF=∠BCH=60°,
∴∠BHF+∠CBH=90°,
∴∠BFH=90°,
∴FH⊥BC,
∵B(6,0),C(3,),
∴直线BC解析式为y=-x+2,
∵H(3,0),
∴直线FH的解析式为y=x-3①,
∵C(3,),
∴直线OC的解析式为y=x②,
联立①②得,点E(,),
∴OE=3;
(3)如图2.∵A(2,0),B(6,0),C(3,),
∴AC2+BC2=4+12=16=AB2,
∴△ABC是直角三角形,即:∠ACB=90°,
∵点D是AB中点,
∴D(4,0),CD=AB=2,
∵△ABP是直角三角形,
∴∠APB=90°,
①点P和点C重合,即:P(3,);
②∵∠APB=90°,
∴PD=AB=2,
∵P在CD上,
∴D点D也是CP的中点,
∴P(5,-);
即:满足条件的点P(3,)或(5,-).
14.2或5
15.解:(1)∵Rt△ABC中,AC=4cm,BC=3cm,
∴.
①如图1,△PQA∽△BCA时,
,解得,
②如图2,△PQA∽△CBA时,
,解得,
又∵0<t<4,
∴或时,以P、Q、A为顶点的三角形与△ABC相似;
(2)能成为等腰三角形.
①当AP=AQ时,
则5-t=t,
解得;
②当AQ=PQ时,如图,过点Q作QD⊥AB,垂足为D,
∵△ACB∽△ADQ,
∴,即
解得;
③当AP=PQ时,过点P作PE⊥AC,垂足为点E,
∵△ABC∽△APE,
∴,即,
解得,
综上,或或.
16.解:(1)分别过点D、A作DF⊥BC、AG⊥BC,垂足为F、G
如图
∴DF∥AG,=
∵AB=AC=10,BC=16,
∴BG=8,
∴AG=6.
∵AD=BE=t,
∴BD=10-t,
∴=
解得DF=(10-t)
∵S△BDE=BE DF=7.5
∴(10-t) t=15
解得t=5.
答:t为5秒时,△BDE的面积为7.5cm2.
(2)存在.理由如下:
①当BE=DE时,△BDE∽△BCA,
∴=即=,
解得t=,
②当BD=DE时,△BDE∽△BAC,
=即=,
解得t=.
答:存在时间t为或秒时,使得△BDE与△ABC相似.
第2页,共2页
第1页,共3页
证明题存在性问题专练1(难点突破)
如图,正方形ABCD的边长为2, E是CD中点, 点P在射线AB上,过点P作线段AE的垂线段, 垂足为F.
(1)求证:△PAF∽△AED;
(2)连接PE, 若存在点P使△PEF与△AED相似,直接写出PA的长.
如图1,在平行四边形ABCD中,AB=3cm,BC=5cm,AC⊥AB,△ACD沿AC的方向匀速平移得到△PNM,速度为1cm/s;同时点Q从点C出发,沿着CB方向匀速移动,速度为1cm/s;当△PNM停止移动时,点Q也停止移动,如图2,设移动时间为ts(0<t<4).连接PQ,MQ,MC.解答下列问题.
(1)当t为何值时,PQ∥MN?
(2)是否存在某一时刻t,使PQ⊥MQ?若存在,求出t的值;若不存在,请说明理由.
如图一,在矩形纸片中,,点分别在边上移动,沿折叠纸片使点落在边上的处,过点作交于点,连接.
求证:四边形为菱形;
如图二,当点与点重合时,求菱形的边长;
当点在移动时,是否存在EMF为等边三角形,若存在,求出此时菱形的边长;若不存在,请说明理由.
如图,直线AB分别与两坐标轴交于点A(4,0).B(0,8),点C的坐标为(2,0).
(1)求直线AB的解析式;
(2)在线段AB上有一动点P.
①过点P分别作x,y轴的垂线,垂足分别为点E,F,若矩形OEPF的面积为6,求点P的坐标.
②连结CP,是否存在点P,使与相似,若存在,求出AP的长,若不存在,请说明理由.
如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD⊥AB于点D.点P从点D出发,沿线段DC向点C运动,点Q从点C出发,沿线段CA向点A运动.两点同时出发.速度都为每秒1个单位长度,当点P运动到C时,两点都停止.设运动时间为t秒.
(1)求线段CD的长;
(2)设△CPQ的面积为S,求S与t之间的函数关系式,并确定在运动过程中是否存在某一时刻t,使得S△CPQ:S△ABC=9:100?若存在,求出t的值;若不存在,说明理由.
如图,在Rt△ABC中,∠B=90°,AB=3cm,BC=4cm.点P从点A出发,以1cm/s的速度沿AB运动;同时,点Q从点B出发,以2cm/s的速度沿BC运动.当点Q到达点C时,P、Q两点同时停止运动.
(1)当运动时间t为何值时,以P、B、Q为顶点的三角形与△ABC相似
(2)是否存在某一时刻t,△PBQ的面积恰为3cm2 若存在,求出运动时间t;若不存在,请说明理由.
如图1,在Rt△ACB中,∠ACB=90°,AB=10,BC=6,点D、F分别是边AC、BC上的动点,过点D作AB的垂线,垂足为E,连接FD,FE.设C、D两点之间的距离为x,C、F两点之间的距离为y.
(1)当DE=4时,求x的值;
(2)如图2,以FD,FE为邻边作 FDGE,当x=3时,是否存在y,使得 FDGE的顶点G恰好落在△ABC的边上?若存在,请求出y的值,若不存在,请说明理由.
如图,在平面直角坐标系中,已知△ABC,点A的坐标是(4,0),点B的坐标是(2,3),点C在x轴的负半轴上,且AC=6.
(1)直接写出点C的坐标;
(2)在y轴上是否存在点P,使得三角形POB的面积等于三角形ABC的?若存在,求出点P的坐标;若不存在,请说明理由;
(3)把点C往上平移3个单位得到点H,作射线CH,连接BH,点M在射线CH上运动(不与点C、H重合).直接写出∠HBM,∠BMA,∠MAC之间的数量关系.
如图,已知矩形ABCD中,AB=10cm,BC=20cm,两只蚂蚁P和Q同时分别从A、B出发,沿AB、BC向B、C方向前进,P蚂蚁每秒钟走1cm,Q蚂蚁每秒钟的速度是P蚂蚁的速度的2倍,结果同时到达B和C点,
(1)都爬行4秒钟后,两蚂蚁的最短距离PQ长是多少cm?
(2)两蚂蚁同时出发t秒钟后,以P、B、Q为顶点的三角形与以A、B、D为顶点的三角形相似,求t的值;
(3)是否存在这样的t(秒)值,使PQ// AC?若存在,求出t的值,若不存在,请说明理由.
如图,在平面直角坐标系中,已知△ABC,点A的坐标是(4,0),点B的坐标是(2,3),点C在x轴的负半轴上,且AC=6.
(1)直接写出点C的坐标;
(2)在y轴上是否存在点P,使得S△POB=S△ABC若存在,求出点P的坐标;若不存在,请说明理由;
(3)把点C往上平移3个单位得到点H,作射线CH,连接BH,点M在射线CH上运动(不与点C、H重合).试探究∠HBM,∠BMA,∠MAC之间的数量关系,并证明你的结论.
如图,直线AB分别与两坐标轴交于点A(4,0).B(0,8),点C的坐标为(2,0).
(1)求直线AB的解析式;
(2)在线段AB上有一动点P.
①过点P分别作x,y轴的垂线,垂足分别为点E,F,若矩形OEPF的面积为6,求点P的坐标.
②连结CP,是否存在点P,使与相似,若存在,求出点P的坐标,若不存在,请说明理由.
如图,在等腰Rt△ABC中,∠ACB=90°,AB=,点D,E分别在边AB,BC上,将线段ED绕点E按逆时针方向旋转90°得到EF。
(1)如图①,若AD=BD,点E与点C重合,AF与DC相交于点O。
求证:BD=2DO;
(2)已知点G为AF的中点。
①如图②,若AD=BD,CE=2,求DG的长;
②若AD=6BD,是否存在点E,使得△DEG是直角三角形?若存在,求CE的长;若不存在,试说明理由。
如图1,已知点A(x1,0),B(x2,0),其中x1,x2是方程x2-8x+12=0的两根,且x1<x2,C(3,).
(1)求点A、B的坐标.
(2)作CH⊥AB于H,设E为OC延长线上一点,连EH交线段BC于F,问是否存在点E,使△CHF与△BEF相似?如果存在,求OE的长,如果不存在,说明理由.
(3)如图2,取AB的中点D,问在直线CD上是否存在点P,使△ABP是直角三角形?若存在,求出所有符合条件的P点的坐标;若不存在,请说明理由.
如图,正方形ABCD的边长为4,E是CD中点,点P在射线AB上,过点P作线段AE的垂线段,垂足为F.
(1)求证:△PAF∽△AED;
(2)连接PE,若存在点P使△PEF与△AED相似,直接写出PA的长______.
如图,在Rt△ABC 中,AC=4cm , BC=3cm,点P由B出发沿BA的方向向点A匀速运动,速度为1 cm /s,同时点Q由 A出发沿AC的方向向点C匀速运动,速度为1cm /s,连接PQ,设运动的时间为t(s),其中0<t<4,解答下列问题:
(1)当t为何值时,以P、Q、A为顶点的三角形与△ABC相似?
(2)点P、Q在运动过程中,△CPQ能否成为等腰三角形?若能,请求出此时t的值,若不存在,请说明理由.
如图所示,在等腰△ABC中,AB=AC=10cm,BC=16cm.点D由点A出发沿AB方向向点B匀速运动,同时点E由点B出发沿BC方向向点C匀速运动,它们的速度均为1cm/s.连接DE,设运动时间为t(s)(0<t<10),解答下列问题:
(1)当t为何值时,△BDE的面积为7.5cm2;
(2)在点D,E的运动中,是否存在时间t,使得△BDE与△ABC相似?若存在,请求出对应的时间t;若不存在,请说明理由.
参考答案
1.(1)证明:∵正方形ABCD,
∴CD∥AB,∠D=90°
∴∠AED=∠PAF,
又∵PF⊥AE,
∴∠PFA=∠D=90°.
∴△PFA∽△ADE.
(2)情况1,当△EFP∽△ADE,且∠PEF=∠EAD时,
则有PE∥AD
∴四边形ADEP为矩形.
∴PA=ED=1;
情况2,当△PFE∽△ADE,且∠PEF=∠AED时,
∵∠PAF=∠AED,
∴∠PEF=∠PAF.
∴PE=PA.
∵PF⊥AE,
∴点F为AE的中点.
∵AE==,
∴AF=,
∵△PFA∽△ADE,
=,
∴=,
∴PA=
∴满足条件的PA的值为1或.
2.解:(1)在Rt△ABC中,,
由平移的性质得MN∥AB,
∵PQ∥MN,
∴PQ∥AB,
∴,
∴,
解得;
(2)若PQ⊥MQ,
则∠PQM=∠PEQ,
∵∠MPQ=∠PQE,
∴△PEQ∽△MQP,
∴,
∴PQ2=MP EQ,
∴PE2+EQ2=MP EQ,
∵,
∴,
∴,
∴t1=0(舍去),,
∴时,PQ⊥MQ.
3.解:(1)证明:∵折叠纸片使A点落在边AD上的E处,折痕为MN
∴点A与点E关于MN对称
∴AM=EM,AF=EF,∠AMF=∠EMF
又∵EF∥AD
∴∠AMF=∠EFM
∴∠EMF=∠EFM
∴ME=EF
∴AM=MF=EF=AF
∴四边形AMEF为菱形;
(2)当点与点重合时
∵四边形ABCD是矩形
∴BC=AD=6cm,CD=AB=10cm,∠BAD=∠D=90°
∵点A与点E关于MN对称
∴BE=AB=10cm
在Rt△BCE中,
∴DE=CD-CE=2cm
在Rt△MDE中,ME=AM=6-DM
∴ME2=DE2+DM2
即:
解得:
∴菱形BFEP的边长为cm;
(3)存在,理由如下:
当EMF为等边三角形时
又∵在△MEN中,MN=2ME
∴
解得:ME=4cm
当菱形的边长为4cm时,EMF为等边三角形
4.解:(1)设直线AB的解析式为y=kx+b,
∵A(4,0),B(0,8),
∴,
∴,
∴y=-2x+8;
(2)①设点P (x,-2x+8),则PE=x,PF=-2x+8,
∴S OEPF=PE PF=x(-2x+8)=6,
∴x1=1,x2=3;
经检验x1=1,x2=3都符合题意,
∴点P(1,6)或(3,2);
②∵△ACP和△AOB中,∠BAO=∠BAO,
∴只有以下两种情况,
当△ACP∽△AOB时,
∵A(4,0),B(0,8),C(2,0),
∴OA=4,OB=8,OC=2,
∴AC=OC=2,
在△AOB中,∠AOB=90°,
∴AB2=OA2+OB2,
即AB2=42+82,
∴AB=(负值舍去),
∵△ACP∽△AOB,
∴,
即,
解得:AP=;
当△APC∽△AOB时,
∴,
即,
解得:,
综上所述,当AP=或时,△ACP与△AOB相似.
5.解:(1)∵∠ACB=90°,AC=8,BC=6,
∴AB===10,
∵AC BC=AB CD,
∴×8×6=×10CD,
解得:CD=4.8;
(2)AD===6.4,
过点Q作QH⊥CD于H,如图所示:
∵CD⊥AB,
∴QH∥AD,
∴△CHQ∽△CDA,
∴=,即=,
∴QH=0.8t,
∴S=QH CP=×0.8t×(4.8-t)=-0.4t2+1.92t;
∵S△ABC=AC BC=×8×6=24,
S△CPQ:S△ABC=9:100,即:=,
整理得:5t2-24t+27=0,
解得:t1=3,t2=1.8,
∴在运动过程中存在某一时刻t,使得S△CPQ:S△ABC=9:100,t的值为:3或1.8.
6.解:(1)由题意得,t秒时,PB=(3-t)cm,BQ=2tcm,
①当△PBQ∽△ABC时,则,
即,
解得t=;
②当△QBP∽△ABC时,则,
即,
解得.
综上,当t=s或s时,△PBQ与△ABC相似;
(2)设经过t秒,△PBQ的面积等于3cm2.
∵,
∴-t2+3t-3=0,
∵△=b2-4ac=32-4(-1)(-3)=9-12=-3<0,
∴此方程无解,
故不存在某一时刻t,△PBQ的面积恰为3cm2.
7.解:(1)∵DE⊥AB,AC⊥BC,
∴∠AED=∠C=90°.
∵∠A=∠A,
∴△ADE∽△ABC.
∴.
∴,
∴AD=.
在Rt△ABC中,
∵∠ACB=90°,AB=10,BC=6,
∴AC==8.
∴CD=AC-AD=8-=.
∴.
(2)存在,理由:
①如下图,G落在AC上,
∵EF∥AC,
∴△EBF∽△ABC,
∴.
设BF=3k,EB=5k,
∴AE=10-5k,
∵DC=3,
∴AD=8-3=5.
由(1)知:△ADE∽△ABC,
∴.
∴AE=4,
∴10-5k=4,
∴,
∴,
∴.
②如下图,G落在AB上,
∵DF∥AB,
∴△DFC∽△ABC,
∴.
∴
∴y=.
综上,当x=3时,存在y=或.,使得 FDGE的顶点G恰好落在△ABC的边上.
8.解:(1)∵A(4,0),
∴OA=4,
∵AC=6,
∴OC=2,
∴C(-2,0);
(2)在y轴上存在点P,使得三角形POB的面积等于三角形ABC的,
设P(0,m),
由题意: |m| 2=××6×3,
解得,
m=±6,
∴P(0,6)或(0,-6);
(3)①当点M在点H的上方时,∠MAC=∠AMB+∠HBM,
理由:设AM交BH于J,
∵BH∥AC,
∴∠CAM=∠HJM,
∵∠HJM=∠AMB+∠HBM,
∴∠MAC=∠AMB+∠HBM,
②当点M在线段CH上(不与C,H重合)时,
∠AMB=∠CAM+∠HBM,
理由:作MK∥HB,
∵HB∥AC,
∴MK∥AC,
∴∠HBM=∠BMK,
∠CAM=∠KMA,
∴∠AMB=∠BMK+∠AMK=∠CAM+∠HBM.
9.解:(1)∵两只蚂蚁P和Q同时分别从A,B出发,沿AB,BC向B,C方形前进,蚂蚁P每秒走1cm,蚂蚁Q每秒走2cm,
∴都爬行4秒后,AP=4cm,BQ=8cm,
则BP=6cm,故PQ==10(cm),
则都爬行4秒后,两蚂蚁的最短距离PQ是10cm;
(2)设t秒时,由题意可得:BP=(10-t)cm,BQ=2tcm,
∠PBQ=∠ADC=90°,则需分下列两种情况讨论:
①当△ PBQ∽△BAD时,
则=,
即=,
解得:t=5,
②当△ QBP∽△BAD时,
则=,
即=,
解得:t=2,
综上,以P,B,Q为顶点的三角形与以A,B,D为顶点的三角形相似时,t=2s或5s.
(3)若PQ//AC,
则△PBQ∽△ABC,
∴=,
∴=,
解得t=5,
∴存在这样的t(秒)值,使PQ // AC,
此时t=5秒.
10.解:(1)∵A(4,0),
∴OA=4,
∵AC=6,
∴OC=2,
∴C(-2,0).
(2)设P(0,m),
由题意: |m| 2=××6×3,
解得m=±6,
∴P(0,6)或(0,-6).
(3)①当点M在点H的上方时,∠MAC=∠AMB+∠HBM.
理由:设AM交BH于J.
∵BH∥AC,
∴∠CAM=∠HJM,
∵∠HJM=∠AMB+∠HBM,
∴∠MAC=∠AMB+∠HBM.
②当点M在线段CH上(不与C,H重合)时,∠AMB=∠CAM+∠HBM.
理由:作MK∥HB.
∵HB∥AC,
∴MK∥AC,
∴∠HBM=∠BMK,∠CAM=∠KMA,
∴∠AMB=∠BMK+∠AMK=∠CAM+∠HBM.
11.解:(1)设直线AB的解析式为y=kx+b,
依题意,,
∴,
∴y=-2x+8;
(2)①设动点P (x,-2x+8),
则PE=x,PF=-2x+8,
∴S OEPF=PE PF=x(-2x+8)=6
∴x1=1,x2=3;
经检验x1=1,x2=3都符合题意,
∴点P(1,6)或(3,2);
②存在,分两种情况
第一种:CP∥OB,
∴△ACP∽△AOB,
而点C的坐标为(2,0),
∴点P(2,4 );
第二种CP⊥AB,
∵∠APC=∠AOB=90°,∠PAC=∠BAO,
∴△APC∽△AOB,
∴,
∴,
∴AP=,
如图,过点P作PH⊥x轴,垂足为H,
∴PH∥OB,
∴△APH∽△ABO,
∴,
∴,
∴PH=,
∴,
∴点P().
∴点P的坐标为(2,4)或点P().
12.解:(1)由旋转的性质得:CD=CF,∠DCF=90°
∵△ABC是等腰直角三角形,AD=BD
∴∠ADO=90°,CD=BD=AD
∴∠DCF=∠ADC
在△ADO和△FCO中,
∴△ADO≌△FCO(AAS)
∴DO=CO
∴BD=CD=2DO
(2)①如图,分别过点D,F作DN⊥BC于点N,FM⊥BC于点M,连结BF
∴∠DNE=∠EMF=90°
又∵NDE=∠MEF,DE=EF
∴△DNE≌△EMF(AAS)
∴DN=EM
又∵,∠ABC=45°
∴DN=EM=7
∴BM=BC-ME-EC=5
∴MF=NE=NC-EC=5
∴
∵点D,G分别是AB,AF的中点
∴
②过点D作DH⊥BC于点H
∵AD=6BD,
∴
(ⅰ)当∠DEG=90°时,有如图②,③两种情况,设CE=t
∵∠DEF=90°,∠DEG=90°
∴点E在线段AF上
∴BH=DH=2,BE=14-t,HE=BE-BH=12-t
∵△DHE∽△ECA
∴,即,解得
∴或
(ⅱ)当DG∥BC时,如图④,过点F作FK⊥BC于点K,延长DG交AC于点N,延长AC并截取MN=NA,连结FM,则NC=DH=2,MC=10
设GN=t,则FM=2t,BK=14-2t
∵△DHE△EKF
∴DH=EK=2,HE=KF=14-2t
∵MC=FK
∴14-2t=10
解得t=2
∵GN=EC=2,GN∥EC
∴四边形GECN为平行四边形,∠ACB=90°
∴四边形GECN为矩形
∴∠EGN=90°
∴当EC=2时,有∠DGE=90°
(ⅲ)当∠EDG=90°时,如图⑤,过点G,F分别作AC的垂线交射线于点N,M,过点F作FK⊥BC于点K,过点D作GN的垂线交NG的延长线于点P,则PN=HC=BC-HB=12
设GN=t,则FM=2t
∴PG=PN-GN=12-t
∵△DHE△EKF
∴EK=DH=2
∴CE=CK-KE=2t-2
∴HE=HC-CE=12-(2t-2)=14-2t
∴FK=HE=14-2t,AM=AC+CM=AC+FK=14+14-2t=28-2t
∴,NC=MN-CM=t
∴PD=t-2
∵△GPD∽△DHE
∴,即
解得,(舍去)
∴
综上所述,CE的长为、或.
13.解:(1)∵x1,x2是方程x2-8x+12=0的两根,
∴x1=2,x2=6,∴A(2,0),B(6,0);
(2)存在,理由:如图1,由(1)知,B(6,0),
∵CH⊥AB于H且C(3,),
∴H(3,0),
∴OH=BH=3,
∵CH=,在Rt△BCH中,tan∠CBH=,
∴∠CBH=30°,
∴∠BCH=60°,
∵点E在OC延长线上,
∴∠CHF<90°,
∵△CHF与△BEF相似,
∴△CHF∽△HBF,
∴∠BHF=∠BCH=60°,
∴∠BHF+∠CBH=90°,
∴∠BFH=90°,
∴FH⊥BC,
∵B(6,0),C(3,),
∴直线BC解析式为y=-x+2,
∵H(3,0),
∴直线FH的解析式为y=x-3①,
∵C(3,),
∴直线OC的解析式为y=x②,
联立①②得,点E(,),
∴OE=3;
(3)如图2.∵A(2,0),B(6,0),C(3,),
∴AC2+BC2=4+12=16=AB2,
∴△ABC是直角三角形,即:∠ACB=90°,
∵点D是AB中点,
∴D(4,0),CD=AB=2,
∵△ABP是直角三角形,
∴∠APB=90°,
①点P和点C重合,即:P(3,);
②∵∠APB=90°,
∴PD=AB=2,
∵P在CD上,
∴D点D也是CP的中点,
∴P(5,-);
即:满足条件的点P(3,)或(5,-).
14.2或5
15.解:(1)∵Rt△ABC中,AC=4cm,BC=3cm,
∴.
①如图1,△PQA∽△BCA时,
,解得,
②如图2,△PQA∽△CBA时,
,解得,
又∵0<t<4,
∴或时,以P、Q、A为顶点的三角形与△ABC相似;
(2)能成为等腰三角形.
①当AP=AQ时,
则5-t=t,
解得;
②当AQ=PQ时,如图,过点Q作QD⊥AB,垂足为D,
∵△ACB∽△ADQ,
∴,即
解得;
③当AP=PQ时,过点P作PE⊥AC,垂足为点E,
∵△ABC∽△APE,
∴,即,
解得,
综上,或或.
16.解:(1)分别过点D、A作DF⊥BC、AG⊥BC,垂足为F、G
如图
∴DF∥AG,=
∵AB=AC=10,BC=16,
∴BG=8,
∴AG=6.
∵AD=BE=t,
∴BD=10-t,
∴=
解得DF=(10-t)
∵S△BDE=BE DF=7.5
∴(10-t) t=15
解得t=5.
答:t为5秒时,△BDE的面积为7.5cm2.
(2)存在.理由如下:
①当BE=DE时,△BDE∽△BCA,
∴=即=,
解得t=,
②当BD=DE时,△BDE∽△BAC,
=即=,
解得t=.
答:存在时间t为或秒时,使得△BDE与△ABC相似.
第2页,共2页
第1页,共3页
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
