山东省济南市长清区第一高级中学2022届高三上学期11月阶段性检测数学试卷(PDF版,含解析)
文档属性
| 名称 | 山东省济南市长清区第一高级中学2022届高三上学期11月阶段性检测数学试卷(PDF版,含解析) |  | |
| 格式 | |||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-03 13:43:22 | ||
图片预览




文档简介
数学
本试卷共 5页,共 150分,考试时间 120分钟.
注意事项:
1.答题前,考生先将自己的姓名、考生号、座号填写在相应位置,认真核对条形码上的
姓名、考生号和座号,并将条形码粘贴在指定位置上。
2.选择题答案必须使用 2B铅笔(按填涂样例)正确填涂,非选择题答案必须使用 0. 5
毫米黑色签字笔书写,字体工整、笔迹清楚。
3.请按照题号在各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、
试题卷上答题无效。保持卡面清洁,不折叠、不破损。
一、单项选择题(本题共 8小题,每小题 5分,共 40分. 在每小题给出的四个选项中,
只有一项是符合题目要求.)
1.集合 P x x 1 ,集合Q x ax 1 0 ,若Q Р,那么实数 a的所有可能取值
的集合为( )
A. 1 B. 1 C. 1,1 D. 1,0,1
1 i
2.已知为 i虚数单位,复数 z ,则 z的共轭复数
1 2i z
在复平面内对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
1
3 n.已知正整数 n≥7,若 (x )(1 x) 的展开式中不含 x5的项,则 n的值为( )
x
A.7 B.8 C.9 D.10
4.某款手机软件主要设有“阅读文章”“视听学习”两个学习模块和“每日答题”“每周答
题”“专项答题”“挑战答题”四个答题模块.某人在学习过程中,“阅读文章”不能放首位,
四个答题模块中有且仅有三个答题模块相邻的学习方法种数为( )
A.60 B.240 C.192 D.432
5.已知平面向量 a,b,c满足 b 2 a a b 4, c a c b 3,则 c a 的最小值为( )
A 7. 2 1 B. 1 C. 5 2 D. 7 2
2
1 2
6.已知正实数 a,b满足: 1,则 2ab 3a b的最小值为( )
a b
A. 2 2 B.3 2 2 C.6 D.无最小值
7.设 f (x) x sin x,若 x
1, x2 , 且 f (x1) f (x2),则下列结论中必成立的是( ) 2 2
A 2 2. x1 x2 B. x1 x2 C. x1 x2 D. x1 x2
e x
, x a
8.函数 f x ex ,若存在 x1 R,对任意 x R, f x f x1 ,则实数 a的取
x 1, x a
值范围是( )
试卷第 1页,共 5页
A. ,0 B.( ∞,0)
C.[0,1] D. 0,1
二、多项选择题(本题共 4小题,每小题 5分,共 20分. 在每小题给出的四个选项中,
有多项符合题目要求,全部选对的得 5分,部分选对的得 2分,有选错的得 0分.)
9.在下列函数中,最小值是 2的函数为( )
1 1
A. f x x 2 1 2 B. f x x
0 x
x x 2
x2 4 4
C. f x D. f x x 2 x 0
x2 3 x
10.下列关于成对样本数据的统计分析的判断中正确的有( )
A.若样本相关系数 r 0,则说明成对样本数据没有相关性
B.样本相关系数 r越大,成对样本数据的线性相关性越强
C.用最小二乘法求得的一元线性回归模型的残差和一定是 0
D.决定系数 R2越大,残差平方和越小,模型的拟合效果越好
11.已知甲袋中有 5个大小相同的球,4个红球,1个黑球;乙袋中有 6个大小相同的
球,4个红球,2个黑球,则( )
4
A.从甲袋中随机摸出一个球是红球的概率为
5
2
B.从乙袋中随机摸出一个球是黑球的概率为
3
3
C.从甲袋中随机摸出 2个球,则 2个球都是红球的概率为
5
2
D.从甲、乙袋中各随机模出 1个球,则这 2个球是一红球一黑球的概率为
5
12.已知 f (x)是定义域为R的函数,满足 f (x) f (x 4),f (1 x) f (3 x),当0 x 2
时, f (x) x2 x,则下列说法正确的是( )
A.函数 f (x)在 [2,4]的解析式为 f (x) (x 3)(x 4)
B.函数 f (x)的图象关于直线 x 2对称
C.当0 x 4时, f (x)的最大值为 2
D.当6 x 8时, f (x)
1
的最小值为
2
三、填空题(本题共 4小题,每小题 5分,共 20分. )
13.复兴村村委会以“美丽乡村”为话题,对村民进行了一次问卷调查(一位村民只能参
加一次),参加问卷调查村民的得分 X ~ N 68,198 ,则 P 40 X 82 ______.
附:参考数据与公式: 198 14 X ~ N , 2,若 ,则 P X 0.6826;
试卷第 2页,共 5页
P 2 X 2 0.9544, P 3 X 3 0.9974
14.如图,已知棱长为 1的正四面体 , 为 的中点, 在线段 上.则 +
的最小值为______.
15.19世纪丹麦数学家琴生对数学分析做出卓越贡献,特别是在函数的凹凸性与不等
式方面留下了很多宝贵的成果,定义:函数 f(x)在(a,b)上的导函数为 f x ,f x 在(a,
b)上的导函数为 f x ,若在(a,b)上 f x <0恒成立,则称函数 f(x)在(a,b)上为“严格
m
” x 2凸函数 .若函数 f(x)= e x ln x x 在(1,4)上为“严格凸函数”,则 m的取值范围为
2
_____.
16.设定义域为 x1, x2 的函数 y f x 的图象的为C,图象的两个端点分别为A、 B,
点O为坐标原点,点M 是C上任意一点,向量OA x1, y1 ,OB x2 , y2 ,且满足
x x1 1 x2 0 1 ,又设向量ON OA 1 OB ,现定义“函数 y f x 在
x1, x2 上“可在标准下线性近似”是指 MN k恒成立,其中 k 0为常数.给出下列结论:
①A、 B、 N三点共线;
②直线MN的方向向量可以为 a 0,1 ;
③函数 y 5x2在 0,1 上“可在标准 1下线性近似”;
1 3
④“函数 y x 在 1,2 上“可在标准下线性近似”,则 k 2.
x 2
其中所有正确结论的序号为 ___.
四、解答题(本题共 6小题,共 70分.)
17.(本题满分 10分)已知 an 是公差不为 0的等差数列,若a1,a3,a13是等比数列 bn 的
连续三项.
(1)求数列 bn 的公比;
a 1 1 n S S 1010(2)若 1 ,数列 的前 和为 n且 n ,求 n的最小值.
anan 1 2021
18.(本题满分 12分)在锐角 ABC中,角 A,B,C所对的边分别为 a,b,c,已知
试卷第 3页,共 5页
3cos2C 2sin A B 1
(1)求 cosC;
(2)若 c 1,a b 5,求 ABC 的面积.
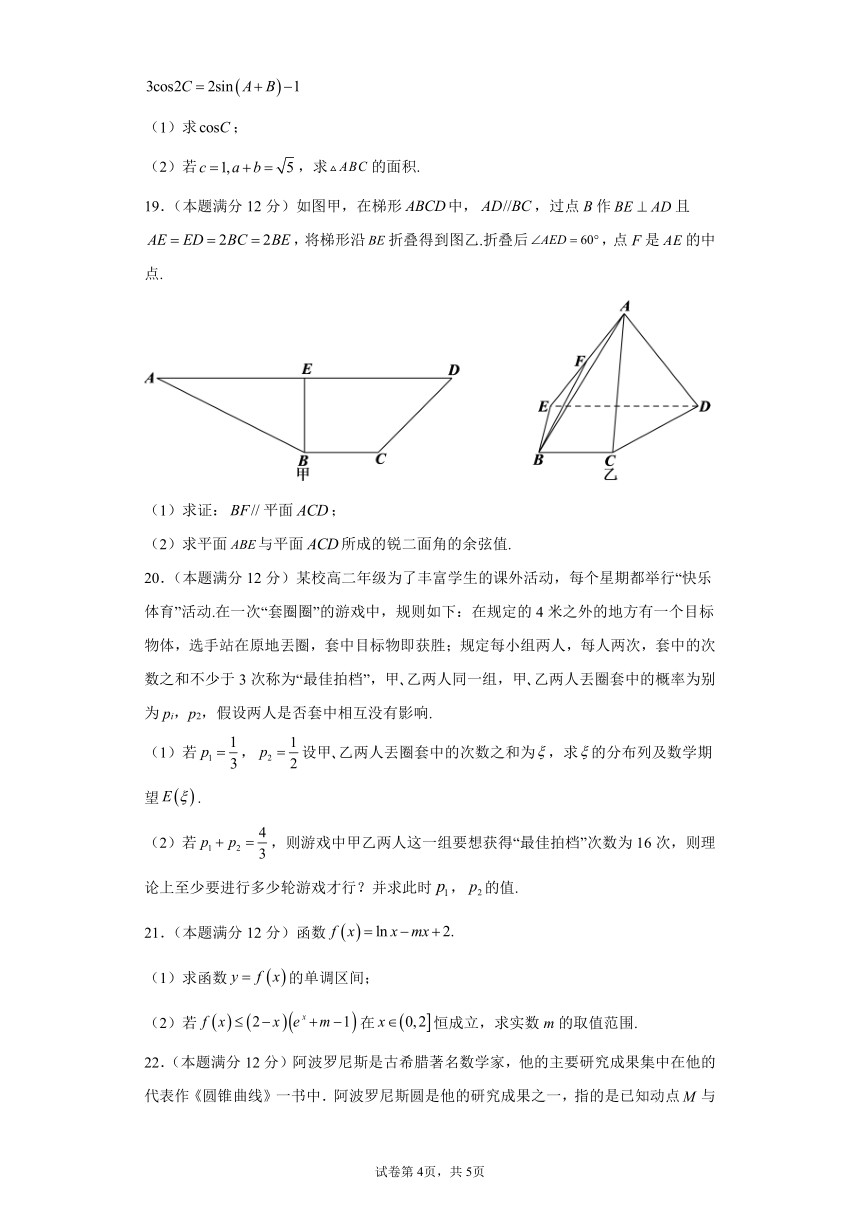
19.(本题满分 12分)如图甲,在梯形 ABCD中, AD//BC,过点 B作 BE AD且
AE ED 2BC 2BE,将梯形沿 BE折叠得到图乙.折叠后 AED 60 ,点 F是 AE的中
点.
(1)求证: BF //平面 ACD;
(2)求平面 ABE与平面 ACD所成的锐二面角的余弦值.
20.(本题满分 12分)某校高二年级为了丰富学生的课外活动,每个星期都举行“快乐
体育”活动.在一次“套圈圈”的游戏中,规则如下:在规定的 4米之外的地方有一个目标
物体,选手站在原地丟圈,套中目标物即获胜;规定每小组两人,每人两次,套中的次
数之和不少于 3次称为“最佳拍档”,甲 乙两人同一组,甲 乙两人丟圈套中的概率为别
为 pi,p2,假设两人是否套中相互没有影响.
1 1
(1)若 p1 , p2 设甲 乙两人丟圈套中的次数之和为 ,求 的分布列及数学期3 2
望 E .
p 4(2)若 1 p2 ,则游戏中甲乙两人这一组要想获得“最佳拍档”次数为 16次,则理3
论上至少要进行多少轮游戏才行?并求此时 p1, p2的值.
21.(本题满分 12分)函数 f x ln x mx 2.
(1)求函数 y f x 的单调区间;
x
(2)若 f x 2 x e m 1 在 x 0,2 恒成立,求实数 m的取值范围.
22.(本题满分 12分)阿波罗尼斯是古希腊著名数学家,他的主要研究成果集中在他的
代表作《圆锥曲线》一书中.阿波罗尼斯圆是他的研究成果之一,指的是已知动点M 与
试卷第 4页,共 5页
MQ
两定点Q, P的距离之比 0, 1 , 是一个常数,那么动点M 的轨迹就
MP
是阿波罗尼斯圆,圆心在直线 PQ上.已知动点M 的轨迹是阿波罗尼斯圆,其方程为
x2 y2 4 x
2 y2
,定点分别为椭圆C : 2 2 1 a b 0 的右焦点 F 与右顶点A,且椭圆Ca b
e 1的离心率为 .
2
(1)求椭圆C的标准方程;
(2)如图,过右焦点 F 斜率为 k k 0 的直线 l与椭圆C相交于 B,D(点 B在 x轴上
方),点S,T 是椭圆C上异于 B,D的两点, SF 平分 BSD,TF平分 BTD.
BS
①求 的取值范围;
DS
81
②将点S、F 、T 看作一个阿波罗尼斯圆上的三点,若△SFT外接圆的面积为 ,求
8
直线 l的方程.
试卷第 5页,共 5页
参考答案
1.D
【分析】
由题得P { 1,1},再对 P分三种情况讨论得解.
【详解】
由题得P { 1,1},
因为Q Р,所以Q ,{ 1},{1} .
当Q 时, a 0;
当Q { 1}时, a ( 1) 1, a 1 ;
当Q {1}时, a (1) 1, a 1 .
所以实数 a的所有可能取值的集合为 1,0,1 .
故选:D
2.A
【分析】
利用复数的除法运算化简 z,求出 z即可得在复平面内对应的点的坐标以及所在的象限.
【详解】
1 i 1 i 1 2i 1 2i 2z i 3 i 3 1 i
1 2i 1 2i 1 2i 1 4i 2 5 5 5 ,
3 1 3 1z i ,所以
5 5 z
在复平面内对应的点坐标为 , ,
5 5
所以 z在复平面内对应的点位于第一象限,
故选:A.
3.D
【分析】
结合二项式的展开式,求出 x5 的项的系数,根据题意建立方程,解方程即可求出结果.
【详解】
(1 x)n k k k的二项展开式中第 k+1 项为Tk 1 Cn ( 1) x
答案第 1页,共 18页
又因为 (x
1
)(1 1 x)n x(1 x)n (1 x)n的展开式不含
x x x
5 的项
4 4 4 1 6 6 6
所以 xCn ( 1) x Cn ( 1) x 0x
C4x5 C6 5n n x 0
C 4即 n C
6
n
所以 n 10,
故选:D.
4.B
【分析】
结合捆绑法、插空法求得不同的学习方法种数.
【详解】
由题意,知有且仅有三个答题模块相邻,所以从四个答题模块中选三个捆绑在一起,和另外
一个答题模块插空放在两个学习模块的间隙或两端位置,由于“阅读文章”不能放首位,因此
不同的学习方法种数为A3C1 A2 A3 24 2 2 4A3 240 .
故选:B
5.D
【分析】
根据已知条件可得 b 4, a 2, a,b
π
,设OA a 2,0 ,OB b 2,2 3 ,3
uuur r
OC c x, y ,可得点C x, y 的轨迹为圆,由圆的性质即可求解.
【详解】
因为 b 2 a a b 4,所以 b 4, a 2,
cos a,b a b 4 1 π
a b 2 4 2 ,因为
0 a,b π,所以 a,b ,
3
uuur r设OA a 2,0 ,OB b 2,2 3 ,OC c x, y ,
c a x 2, y , c b x 2,2 3 y ,
所以 c a c b x 2 x 2 y 2 3 y 3,
答案第 2页,共 18页
2
即 x2 y 3 4 ,
所以点C x, y 在以M 0, 3 为圆心,半径 r = 2的圆上,
2
c a x 2 2 y 2 表示圆 x2 y 3 4 上的点 x, y 与定点 A 2,0 的距离,
2
所以 c a 2的最小值为 MA r 0 2 3 0 2 7 2 ,
故选:D.
6.B
【分析】
1 2
对 1去分母得 2a b ab,代换 2ab 3a b中的 ab,再结合“1”的妙用即可求解
a b
【详解】
1 2
由 1 2a b ab,则 2ab 3a b 4a 2b 3a b a b,
a b
a b a b 1 2 3 2a b 3 2 2 ,当且仅当 时取到等号,故
a b b a b 2a 2 2
2ab 3a b的最小值为3 2 2 .
故选:B
7.C
【分析】
证明函数 f (x) x sin x
的奇偶性,利用导数得出函数 f (x) 在区间 0, 的单调性,利用单调 2
性解不等式,即可得出答案.
【详解】
f ( x) x sin x x sin x f (x),则函数 f (x) x sin x为偶函数
所以 f (x1) f (x2 ) f ( x1 ) f ( x2 )
当 x 0,
时, f (x) (x sin x)
sin x x cos x 0
2
所以函数 f (x)
在区间 0, 上单调递增 2
2 2
所以 x1 x2 x1 x2
故选:C
【点睛】
答案第 3页,共 18页
本题主要考查了函数的奇偶性以及利用单调性解不等式,属于中档题.
8.A
【分析】
e x
根据给定条件可得 f x 在R 上有最大值,再利用导数探求函数 y x 在R 上的最大值,然e
后结合图象分类讨论即可得解.
【详解】
由题意知,在R 上 f x 有最大值,
y e x e 1 x e x由 x 得: y ,于是得当 x 1时, y 0, y x 在 ,1x 上单调递增,e e e
x 1时, y 0, y
e x
x 在 1, y
e x
上单调递减,因此, x 在R 上有最大值且 ye e max
1,此
时 x 1,
当 a 0时,如上左图, x 1 1,在 ( , a) 上存在 x,使得 f x 1,而在 x a, 时,
f x ≤1,因此, f x 在R 上无最大值,不合题意,
当 a 0 时,如上右图, x 1 1,当 x ( ,a) 时, f x 1,在 x a, 时, f x ≤1,
且 x能取到1,因此, f x 在R 上有最大值1,
所以 a的取值范围是 ( , 0].
故选:A
【点睛】
思路点睛:含参数的分段函数问题,参数值影响式子变形或图形绘制时,往往要分类讨论,
需有明确的标准、全面考虑.
9.AD
【分析】
对于 A、D:直接利用基本不等式进行计算即可;
答案第 4页,共 18页
对于 B、C:利用基本不等式取等号的条件不满足可以判断;
【详解】
1 1 2 1
对于 A:因为 x2 0,所以 f x x2 2 x x 12 2 x 2 2(当且仅当 2 即 时等号x x x
成立).故 A 正确;
对于 B f x x 1 2 x 1: 2取等号的条件为 x 1,但是0 x 1 不能取得.故 B 错误;
x x 2
222 x 3 1对于 C: f x x 4 x2 3 1 2,取等号的条件为 x2 3 1,
x2 3 x2 3 x2 3
此时 x2 2无解,所以选项 C 错误;
4 4 4
对于 D:f x x 2 2 x 2 2,(当且仅当 x 即 x 2时等号成立).故 D 正确;
x x x
故选:AD
【点睛】
易错点睛:利用基本不等式求最值时,要注意其必须满足的三个条件:
(1)“一正二定三相等”“一正”就是各项必须为正数;
(2)“二定”就是要求和的最小值,必须把构成和的二项之积转化成定值;要求积的最大值,则
必须把构成积的因式的和转化成定值;
(3)“三相等”是利用基本不等式求最值时,必须验证等号成立的条件,若不能取等号则这个定
值就不是所求的最值,这也是最容易发生错误的地方.
10.CD
【分析】
根据样本相关系数判断 A 和 B,根据一元线性回归模型的最小二乘估计判断 C 和 D.
【详解】
对于选项 A:当 r 0时,只表明成对样本数据间没有线性相关关系,但是不排除它们之间
有其他相关关系. 故 A 错误;
对于选项 B:样本相关系数 r 越大,成对样本数据的线性相关性越强. 故 B 错误;
对于选项 C:残差和为
n n n n n
yi y i yi bxi a yi b xi a ny nbx na n y bx a 0 . 故 C
i 1 i 1 i 1 i 1 i 1
正确;
对于选项 D:决定系数R2 越大,表示残差平方和越小,即模型的拟合效果越好. 故 D 正确.
答案第 5页,共 18页
故选:CD.
11.ACD
【分析】
A.根据红球数与甲袋中总球数的比求得结果;B.根据黑球数与乙袋中总球数的比求得结果;
C.先利用组合数计算出摸出2个球的总的取法数,再分析摸出2个球都是红球的取法数,根
古典概型的概率计算公式求得结果;D.利用概率的乘法公式求得结果即可.
【详解】
4
对选项 A,从甲袋中随机摸一个球是红球的概率为 P ,故 A 对;
5
2 1
对选项 B,从乙袋中随机摸一个球是黑球的概率为 P ,故 B 错;
6 3
C2
对选项 C,从甲袋中随机摸 2 个球,则 2 个球都是红球的概率 P 4
6 3
C2
,故 C 对;
5 10 5
对选项 D,从甲、乙袋中各随机摸出 1 个球,则这 2 个球是一红球一黑球的概率
P 4 1 1 2 2 ;
5 3 5 3 5
故选:ACD.
12.ABC
【分析】
判断出 f x 周期性、对称性、奇偶性,根据解析式的求法判断 A 选项,结合图象判断 CD
选项.
【详解】
f (x) f (x 4) f x 是周期为 4的周期函数,
f (1 x) f (3 x) f (2 x) f (2 x) f x 的对称轴为 x 2,B 正确.
f (2 x) f (2 x) f 4 x f x ,
则 f x f x , f x 为偶函数.
2 x 4时, x 4, 2 , x 4 0,2 ,
f x f x f x 4 x 4 2 x 4 x2 7x 12 x 3 x 4 ,A 正确.
由此画出 f x 在区间 0,8 的图象如下图所示,
答案第 6页,共 18页
1 2
当0 x 2时, f (x) x2 x x 1 1 2 4
, 2 . 4
结合图象可知 C 正确,D 错误.
故选:ABC
13.0.8185
【分析】
根据正态分布的性质,进行计算概率即可得解.
【详解】
由 X ~ N 68,198 可得 68, 198 14,
P 40 X 82 P 2 X P 2 X 2 P X
2 2
0.9544 0.6826
0.8185 .
2 2
故答案为:0.8185
14. 1 + 6
3
【解析】
【详解】
记∠ = .在 中, = 1, = = 3.故 cos = 3 , sin = 6.
2 3 3
如图,将 绕 旋转,使 在平面 内,此时 在 '处.联结 '、 ' .
则所求的最小值即为 '的长.易知∠ ' = + 30°.故 '2 = 2 + '2 2
'cos∠ '
= 12 + 12 2cos + 30° = 2 2 cos cos30° sin sin30° = 1 + 6.
3
答案第 7页,共 18页
从而, ' = 1 + 6.
3
故答案为: 1 + 6
3
1
15 4.[e , )
4
【分析】
求出函数 f(x)的导数 f x ,再对 f x 求导并根据给定定义列出恒成立的不等式即可得解.
【详解】
ex x ln x m 1因函数 f(x)= x2 ,则 f (x) ex 1 ln x mx, f (x) ex m,
2 x
x 1
依题意, x (1, 4), f (x) 0 e m 0 m ex
1 y ex 1 ,而函数 在(1,4)上单调
x x x
递增,
ex 1 e4 1 4 1即 ,因此,m e ,
x 4 4
1
所以 m 4的取值范围为[e , ) .
4
[e4 1故答案为: , )
4
16.①②④
【分析】
根据题意得到 BN BA得到①正确,计算得到 xN x得到MN∥ y
1
轴,②正确,取 ,
2
5 3 1 1
计算得到 MN 1,③错误, MN y
4 M
yN x 2 2 x
,根据均值不等式得到答案.
【详解】
ON OA 1 OB ,即ON OB OA OB,即 BN BA,故A 、 B、N三点共线,
答案第 8页,共 18页
①正确;
ON OA 1 OB ,OA x1, y1 ,OB x2 , y2 ,故 xN x1 1 x2,
x x1 1 x2 0 1 ,故 xN x,即MN∥ y轴,即直线MN的方向向量可以为
a 0,1 ,②正确;
OB 1,5 1 1 1 1 M 1 5易知OA 0,0 , ,取 ,则 x x1 x ,故 , ,2 2 2 2 2 2 4
1 ON OA 1 1 5 1 5
OB , ,故 N
, MN 5 ,即 1,③错误;2 2 2 2 2 2 4
y x 1 1,2 A 1,0 B 2, 3 y 3 x 3函数 在 上,易知 ( ), ,故直线 AB方程为: .x 2 2 2
MN y y x 1 3 3 3 1 1 3M N x x 2
1 3
2 ,
x 2 2 2 2 x 2 2 2
1
当且仅当 x
1
,即 x 2 时等号成立,故④正确.
2 x
故答案为:①②④.
【点睛】
本题考查了向量共线问题,方向向量,均值不等式求最值,意在考查学生的计算能力和综合
应用能力,其中把向量模长转化为点的纵坐标相减是解题的关键.
17.(1)5;(2)1011.
【分析】
a
(1)用基本量表示 a1,d
2 3
,可得 a1 2d a1 a1 12d ,解得 d 2a1 ,结合 q a 可得解;1
(2)裂项相消法求和,解不等式即得解.
【详解】
(1)设等差数列 an 的公差为 d,由 a1,a3,a13是等比数列 bn 的连续三项,
2
得 a3 a1 a13 ,即 a1 2d
2 a1 a1 12d 2,化简得 4d 8a1d .
d 0, d 2a1.
设数列 bn 的公比的公比为q q
a3 a1 2d a 4a 1 1,则 5a .1 a1 a1
1 1 1 1 1
(2)若 a1 1,则 d 2,an 2n 1, anan 1 (2n 1)(2n 1) 2
2n 1 2n 1
,
答案第 9页,共 18页
S 1 1 1 1 1 n 2 1 3 3 5 5 7 (2 n 1) (2 n 1)
1 1 1 1 1 1 1 1 1 1 1 1 n .2 3 3 5 5 7 2 n 1 2 n 1 2 2 n 1 2 n 1
由 S
1010 n 1010
n ,得 , n 1010 ,故 n的最小值为 1011.2021 2n 1 2021
18.
(1 5)
3
2 3- 5( )
2
【分析】
(1)先由三角形内角和定理、诱导公式、二倍角公式得到关于 sinC的一元二次方程,再利
用同角三角函数基本关系进行求解;
(2)先利用余弦定理和整体思想求得 ab值,再利用三角形的面积公式进行求解.
(1)
解:因为3cos2C 2sin A B 1,
所以3(1 2sin 2 C) 2sin C 1 ,
即6sin2 C+2sinC 4=0,
即3sin2 C+sinC 2=0,
解得 sinC=
2
或 sinC 1(舍),
3
又因为 ABC是锐角三角形,
所以 cosC 1 sin2C 5 .
3
(2)
解:由(1)得: cosC 1 sin2C 5 ,
3
由c 1,a b 5 和余弦定理,得:
a b 5
,
a2 b2
2 5
ab 1
3
则 (a b)2 (a 2 b2 2 5 ab) 4
3
答案第 10页,共 18页
6 3(3 5)
解得 ab = ,
3+ 5 2
所以 ABC的面积公式为
S 1 ab sinC 1 3(3 5) 2 3 5 .
2 2 2 3 2
19.
(1)证明见解析
2 7( )
7
【分析】
(1)取 AD的中点 G,连接 FG、CG,根据平面几何知识证得四边形 BCGE 是平行四边形,
有BF //CG,由线面平行的判定可得证;
(2)以 O为坐标原点, OC所在的直线为 x轴,以OD,OA的方向分别为 y,z轴的正方
向,建立如图所示的空间直角坐标系 O-xyz,由二面角的空间向量求解方法可求得答案.
(1)
1
证明:取 ED的中点 G,连接 FG、CG,因为点 F是 AE的中点,所以 FG //ED,FG ED,
2
又 AD//BC,过点 B作 BE AD且 AE ED 2BC 2BE,所以 BC //ED,BC
1
ED,,
2
所以 FG //BC,FG BC,所以四边形 BCGE 是平行四边形,所以 BF //CG,又 BF 面 ACD,
CG 面 ACD,所以BF // 面 ACD .
(2)
解:取 BD的中点O,连接 CO、AO,因为 BE ED,BE AE,ED AE E,所以BE 面 AED,
又CO//EB,所以CO 面 AED,
又 AED 60 , AE ED,所以 AED是正三角形, AO ED,
所以以 O为坐标原点, OC所在的直线为 x轴,以OD,OA的方向分别为 y,z轴的正方向,
建立如图所示的空间直角坐标系 O-xyz.
设 BC 1,则B 1, 1,0 ,C 1,0,0 ,D 0,1,0 ,A 0,0, 3 ,E 0, 1,0 ,从而 AC 1,0, 3 ,
答案第 11页,共 18页
AD 0,1, 3 , AE 0, 1, 3 , AB 1, 1, 3 .
设平面 ACD的法向量为 n x1, y1, z1 ,
n·AC x1 3z1 0,
则 令 z1 1,得 n 3, 3,1 .
n·AD y1 3z1 0,
设平面 AEB的法向量为m x2 , y2 ,z2 ,
m ·AE y2 + 3z2 0,
则 令 z2 1,得m 0, 3,1 .
m·AB x2 y2 3z2 0,
设平面 ABE与平面 ACD所成的锐二面角为 ,
n m 0 3 1
故 cos cos n, m
7
,所以平面 ABE与平面 ACD所成的锐二面角
n m 7 2 7
7
的余弦值为 .
7
5 2
20.(1)分布列答案见解析,数学期望: ;(2)理论上至少要进行 27 轮游戏,p1 p2 .3 3
【分析】
(1)确定 的所有可能取值并计算相应的概率,即可列出分布列,再根据期望公式求 E 即
可;
(2)求出他们在一轮游戏中获“最佳拍档”的概率 P并化简,再由 0 p1 1,0 p2 1,
p 41 p2 ,求出 p1p2 的取值范围,再利用换元法并结合二次函数的性质即可求出 P3 max
,从
而可得n的最小值及此时 p1, p2 的值.
【详解】
解:(1)两人丢圈套中的次数值和为 ,则 的值可能为 0,1,2,3,4,
答案第 12页,共 18页
2 2
P 0 1 1 1 1 1
3 2
,
9
1 2 1 2 2P 1 C 1 1 1 1 1 C 1 1 12 1 ,
3 3 2 3 2 2 2 3
2 2
P 1 1 1 2 1 1 1
2 1 2 13
2 1 C1 C1 3 2 2 1 1
,
3 3 2 2 2 3 2 36
2 2
P 3 1 C 1 1 1 1 C 1 1 2 1 1 3 2 2 2 2
,
3 3 2 6
2 2
P 4 1 1 1 ,
3 2 36
分布列如下表:
0 1 2 3 4
p 1 1 13 1 1
9 3 36 6 36
E 0 1 1 1 13 1 1 5 2 3 4 .
9 3 36 6 36 3
(2)他们在一轮游戏中获“最佳拍档”的概率为
P C12p 1 p C 2 p
2 C 2 p 2C1p 1 p C 2 p 2 2 2 2 21 1 2 2 2 1 2 2 2 2 1 C2 p2 2p1p2 p 1 p2 3 p 1 p 2
,
p p 4 8 2 2因为 1 2 ,所以P p1p2 3 p1 p2 ,3 3
4 1 1
因为 0 p1 1,0 p2 1, p1 p2 ,所以 p1 1, p3 3 3 1
1,
1 2
所以 p1p
4
2 ,令 t p p
1 t 4 P h t 3t 2 8t 3 t 4 161 2,以 ,则 ,9 9 9 9 3 9 27
4 16
当 t 时, P
9 max
,
27
他们小组在n轮游戏中获“最佳拍档”次数 满足 ~ B n, p ,
由 np 16max ,则 n 27,所以理论上至少要进行 27 轮游戏,
此时 p1 p
4 4 2
2 , p1p2 , p p .3 9 1 2 3
答案第 13页,共 18页
1
21.(1)答案见解析;(2) 1 ln2,
.
2
【分析】
(1)求导,分别讨论m 0和m 0两种情况 f x 的正负,即可求得 y f x 的单调区间.
x
(2)所求转化为求 2m 4 x 2 e lnx x在 x 0,2 恒成立问题,设
g x x 2 ex lnx x,利用导数判断其单调性,并求得 g(x)的最大值,可得关于 m的不
等式,即可得答案.
【详解】
1 1 mx
(1) f x m , (x 0).
x x
当m 0时, f x 0,所以 y f x 在 0, 为增函数,
1
当m 0时,令 f (x) 0,解得 x ;
m
x 0, 1 当 时, f x 0, y f x 为增函数,
m
x 1 , 当 时, f x 0, y f x 为减函数,
m
综上:当m 0时, y f x 的单调增区间为 0, ,
1 1
当m 0时, y f x 的单调增区间为 0, ,单调减区间为 , .
m m
(2)因为 f x 2 x e x m 1 在 x 0,2 恒成立,
所以 2m 4 x 2 ex lnx x在 x 0,2 恒成立,
设 g x x 2 ex lnx x g x x 1 ex 1 1 ,则 1 x 1 x
x
e
x
.
设 h x 1 ex ,h x ex 1 0
x x2
所以 h x 在 0,2 1 单调递增,又 h e 2 0,h 1 e 1 0,
2
1
因此存在唯一 x0 ,1 ,使得 h x0 0,
2
所以当 x 0, x0 时, h x 0,
当 x x0 ,1 时, h x 0.
当 x 0, x0 时, g x 0 ,当 x x0 ,1 时, g x 0.
答案第 14页,共 18页
所以函数 g x 在 0, x0 递增,在 x0 ,1 递减,在 1,2 递增
因此 g(x)max max g x0 , g 2 ,
h x e x 1 1由 00 0得 ex0 ,则 lnx0 xx 0 .0 x0
所以 g x0 x 2 ex lnx x
1 1
0
0 0 0 x0 2 2x0 1 2 x0 x x ,0 0
1
因为 x
1
0 ,1
,则 x0 2,所以 g x0 3,
2 x0
因为 g 2 ln2 2 2 ,
所以当 x 0,2 时, g(x)max g 2 ln2 2,
1
所以 2m 4 ln2 2,解得m 1 ln 2
2
所以m 1
1
的取值范围是 ln2,
2
【点睛】
解题的关键是熟练掌握利用导数判断函数单调性,求极(最)值的方法,并灵活应用,在得
到 g x 解析式,并且不能直接判断其正负时,可令 h x g (x) ,再次求导,根据 h x 的
单调性,求得 h x 的值域,进而可得 g x 的正负,即可得 g(x) 的单调性,属中档题.
2 2 1
22 1 x y 1 2 ,1 5 10.( ) = ;( )①
8 6 3
;② y x .
2 2
【分析】
(1)方法 1,利用特殊值法,求得椭圆方程,方法 2,利用定义整理得
x2 y2 2x 2a
2 2x a
2 c 2
0,再根据条件列式求得椭圆方程;方法 3,利用定义进行
2 1 2 1
MF BS BF
整理,由 为常数,求得系数,得到椭圆方程;(2)①首先由面积比值求得 ,
MA DS DF
BF 3
令 ,则 BF FD,利用坐标表示向量,求得 5 2x ,再求范围;②由阿波DF 0
罗尼斯圆定义知,S,T , F 在以 B,D为定点得阿波罗尼斯圆上,由几何关系列式得
答案第 15页,共 18页
BF 2r BF 1 1 2 2x 0 2 2
,求得 r,再根据 BF DF 1 9 ,求得 x0 , y ,即可计DF 2r DF 3 2 2 x
0
2 0
算直线方程.
【详解】
c 2 c 2
(1)方法(1)特殊值法,令M 2,0 , ,且 a 2c,解得 2
a 2 a 2 c 2
2 2
∴ a2 8,b2 a2 c2 6,椭圆C x y的方程为 =18 6
2
MF x c y 2
方法(2)设M x, y ,由题意 (常数),
MA 2x a y 2
x2 y2 2x 2a
2 2x a
2 c 2
整理得: 2 0, 1 2 1
2c 2a 2
0
2 1 c 1
故 ,又 2 ,解得: a 2 2 , c 2 .
a
2 c2 a 2
2 4 1
b2 a2 c2 x
2 y2
∴ 6,椭圆C的方程为 =1.8 6
方法(3)设M x, y ,则 x2 y2 4 .
2 2
MF x c y2 x c 4 x2 c2 4 2cx
由题意
MA 2 2 2x a y2 x a 4 x2 a 4 2ax
MF c2 4 c c 1
∵ 为常数,∴ 2 ,又 ,解得: a
2 8,c2 2,故MA a 2 b
2 a2 c2 6
a 4 a
2 2
∴椭圆C x y的方程为 =1
8 6
1
S SB SF sin BSF SB BF
(2)①由 SBF 2
S
1 ,又
SBF ,
S SDF SD SF sin DSF SD S SDF DF
2
BS BF
∴ (或由角平分线定理得)
DS DF
BF
令 2 2,则 BF FD,设D x0 , y0 ,则有3x 4y 24 ,DF 0 0
答案第 16页,共 18页
xB 2 1 x又直线 l的斜率 k 0,则 x0 2 2, 2 0, 代入3x2 4y2 24 0 得:
yB y0
2
3 2 1 x 4 20 y 20 24 0,即 1 5 3 2 x 0 0,
∵ 0,∴
3 1
,1 .
5 2x 0 3
SB TB BF
②由①知, ,由阿波罗尼斯圆定义知,
SD TD DF
S,T , F 在以 B,D为定点得阿波罗尼斯圆上,设该圆圆心为C1,半径为 r,与直线 l的
另一个交点为 N,
BF NB BF 2r 1 BF r
则有 ,即 ,解得: 1 1 .
DF ND DF 2r DF BF DF
9 1 1 2 2
又 S圆C r
2 81 ,故 r ,∴
1 8 2 2 BF DF 9
又 DF 2 2x 2 y 2 3 10 0 x 20 2 6 x4 0 2 2 x0 ,2
1 1 1 1 5 2x0 1 2 2x 2 2 0
∴ BF DF DF DF 1 ,3 2 2 1 x 1 0 2 2 x2 0 3 2 2 x
9
2 2 0
3 3 10
解得: x 20 , y0 6 x
2
0 ,2 4 4
y 5 5 10
∴ k 0 ,∴直线 l的方程为 y x .
2 x0 2 2 2
【点睛】
答案第 17页,共 18页
关键点点睛:本题考查轨迹问题,考查直线与椭圆的位置关系,以及外接圆,新定义的综合
应用,属于难题,本题的关键是读懂题意,并根据几何关系进行消参,转化与化归,是本题
的关键也是难点.
答案第 18页,共 18页
本试卷共 5页,共 150分,考试时间 120分钟.
注意事项:
1.答题前,考生先将自己的姓名、考生号、座号填写在相应位置,认真核对条形码上的
姓名、考生号和座号,并将条形码粘贴在指定位置上。
2.选择题答案必须使用 2B铅笔(按填涂样例)正确填涂,非选择题答案必须使用 0. 5
毫米黑色签字笔书写,字体工整、笔迹清楚。
3.请按照题号在各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、
试题卷上答题无效。保持卡面清洁,不折叠、不破损。
一、单项选择题(本题共 8小题,每小题 5分,共 40分. 在每小题给出的四个选项中,
只有一项是符合题目要求.)
1.集合 P x x 1 ,集合Q x ax 1 0 ,若Q Р,那么实数 a的所有可能取值
的集合为( )
A. 1 B. 1 C. 1,1 D. 1,0,1
1 i
2.已知为 i虚数单位,复数 z ,则 z的共轭复数
1 2i z
在复平面内对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
1
3 n.已知正整数 n≥7,若 (x )(1 x) 的展开式中不含 x5的项,则 n的值为( )
x
A.7 B.8 C.9 D.10
4.某款手机软件主要设有“阅读文章”“视听学习”两个学习模块和“每日答题”“每周答
题”“专项答题”“挑战答题”四个答题模块.某人在学习过程中,“阅读文章”不能放首位,
四个答题模块中有且仅有三个答题模块相邻的学习方法种数为( )
A.60 B.240 C.192 D.432
5.已知平面向量 a,b,c满足 b 2 a a b 4, c a c b 3,则 c a 的最小值为( )
A 7. 2 1 B. 1 C. 5 2 D. 7 2
2
1 2
6.已知正实数 a,b满足: 1,则 2ab 3a b的最小值为( )
a b
A. 2 2 B.3 2 2 C.6 D.无最小值
7.设 f (x) x sin x,若 x
1, x2 , 且 f (x1) f (x2),则下列结论中必成立的是( ) 2 2
A 2 2. x1 x2 B. x1 x2 C. x1 x2 D. x1 x2
e x
, x a
8.函数 f x ex ,若存在 x1 R,对任意 x R, f x f x1 ,则实数 a的取
x 1, x a
值范围是( )
试卷第 1页,共 5页
A. ,0 B.( ∞,0)
C.[0,1] D. 0,1
二、多项选择题(本题共 4小题,每小题 5分,共 20分. 在每小题给出的四个选项中,
有多项符合题目要求,全部选对的得 5分,部分选对的得 2分,有选错的得 0分.)
9.在下列函数中,最小值是 2的函数为( )
1 1
A. f x x 2 1 2 B. f x x
0 x
x x 2
x2 4 4
C. f x D. f x x 2 x 0
x2 3 x
10.下列关于成对样本数据的统计分析的判断中正确的有( )
A.若样本相关系数 r 0,则说明成对样本数据没有相关性
B.样本相关系数 r越大,成对样本数据的线性相关性越强
C.用最小二乘法求得的一元线性回归模型的残差和一定是 0
D.决定系数 R2越大,残差平方和越小,模型的拟合效果越好
11.已知甲袋中有 5个大小相同的球,4个红球,1个黑球;乙袋中有 6个大小相同的
球,4个红球,2个黑球,则( )
4
A.从甲袋中随机摸出一个球是红球的概率为
5
2
B.从乙袋中随机摸出一个球是黑球的概率为
3
3
C.从甲袋中随机摸出 2个球,则 2个球都是红球的概率为
5
2
D.从甲、乙袋中各随机模出 1个球,则这 2个球是一红球一黑球的概率为
5
12.已知 f (x)是定义域为R的函数,满足 f (x) f (x 4),f (1 x) f (3 x),当0 x 2
时, f (x) x2 x,则下列说法正确的是( )
A.函数 f (x)在 [2,4]的解析式为 f (x) (x 3)(x 4)
B.函数 f (x)的图象关于直线 x 2对称
C.当0 x 4时, f (x)的最大值为 2
D.当6 x 8时, f (x)
1
的最小值为
2
三、填空题(本题共 4小题,每小题 5分,共 20分. )
13.复兴村村委会以“美丽乡村”为话题,对村民进行了一次问卷调查(一位村民只能参
加一次),参加问卷调查村民的得分 X ~ N 68,198 ,则 P 40 X 82 ______.
附:参考数据与公式: 198 14 X ~ N , 2,若 ,则 P X 0.6826;
试卷第 2页,共 5页
P 2 X 2 0.9544, P 3 X 3 0.9974
14.如图,已知棱长为 1的正四面体 , 为 的中点, 在线段 上.则 +
的最小值为______.
15.19世纪丹麦数学家琴生对数学分析做出卓越贡献,特别是在函数的凹凸性与不等
式方面留下了很多宝贵的成果,定义:函数 f(x)在(a,b)上的导函数为 f x ,f x 在(a,
b)上的导函数为 f x ,若在(a,b)上 f x <0恒成立,则称函数 f(x)在(a,b)上为“严格
m
” x 2凸函数 .若函数 f(x)= e x ln x x 在(1,4)上为“严格凸函数”,则 m的取值范围为
2
_____.
16.设定义域为 x1, x2 的函数 y f x 的图象的为C,图象的两个端点分别为A、 B,
点O为坐标原点,点M 是C上任意一点,向量OA x1, y1 ,OB x2 , y2 ,且满足
x x1 1 x2 0 1 ,又设向量ON OA 1 OB ,现定义“函数 y f x 在
x1, x2 上“可在标准下线性近似”是指 MN k恒成立,其中 k 0为常数.给出下列结论:
①A、 B、 N三点共线;
②直线MN的方向向量可以为 a 0,1 ;
③函数 y 5x2在 0,1 上“可在标准 1下线性近似”;
1 3
④“函数 y x 在 1,2 上“可在标准下线性近似”,则 k 2.
x 2
其中所有正确结论的序号为 ___.
四、解答题(本题共 6小题,共 70分.)
17.(本题满分 10分)已知 an 是公差不为 0的等差数列,若a1,a3,a13是等比数列 bn 的
连续三项.
(1)求数列 bn 的公比;
a 1 1 n S S 1010(2)若 1 ,数列 的前 和为 n且 n ,求 n的最小值.
anan 1 2021
18.(本题满分 12分)在锐角 ABC中,角 A,B,C所对的边分别为 a,b,c,已知
试卷第 3页,共 5页
3cos2C 2sin A B 1
(1)求 cosC;
(2)若 c 1,a b 5,求 ABC 的面积.
19.(本题满分 12分)如图甲,在梯形 ABCD中, AD//BC,过点 B作 BE AD且
AE ED 2BC 2BE,将梯形沿 BE折叠得到图乙.折叠后 AED 60 ,点 F是 AE的中
点.
(1)求证: BF //平面 ACD;
(2)求平面 ABE与平面 ACD所成的锐二面角的余弦值.
20.(本题满分 12分)某校高二年级为了丰富学生的课外活动,每个星期都举行“快乐
体育”活动.在一次“套圈圈”的游戏中,规则如下:在规定的 4米之外的地方有一个目标
物体,选手站在原地丟圈,套中目标物即获胜;规定每小组两人,每人两次,套中的次
数之和不少于 3次称为“最佳拍档”,甲 乙两人同一组,甲 乙两人丟圈套中的概率为别
为 pi,p2,假设两人是否套中相互没有影响.
1 1
(1)若 p1 , p2 设甲 乙两人丟圈套中的次数之和为 ,求 的分布列及数学期3 2
望 E .
p 4(2)若 1 p2 ,则游戏中甲乙两人这一组要想获得“最佳拍档”次数为 16次,则理3
论上至少要进行多少轮游戏才行?并求此时 p1, p2的值.
21.(本题满分 12分)函数 f x ln x mx 2.
(1)求函数 y f x 的单调区间;
x
(2)若 f x 2 x e m 1 在 x 0,2 恒成立,求实数 m的取值范围.
22.(本题满分 12分)阿波罗尼斯是古希腊著名数学家,他的主要研究成果集中在他的
代表作《圆锥曲线》一书中.阿波罗尼斯圆是他的研究成果之一,指的是已知动点M 与
试卷第 4页,共 5页
MQ
两定点Q, P的距离之比 0, 1 , 是一个常数,那么动点M 的轨迹就
MP
是阿波罗尼斯圆,圆心在直线 PQ上.已知动点M 的轨迹是阿波罗尼斯圆,其方程为
x2 y2 4 x
2 y2
,定点分别为椭圆C : 2 2 1 a b 0 的右焦点 F 与右顶点A,且椭圆Ca b
e 1的离心率为 .
2
(1)求椭圆C的标准方程;
(2)如图,过右焦点 F 斜率为 k k 0 的直线 l与椭圆C相交于 B,D(点 B在 x轴上
方),点S,T 是椭圆C上异于 B,D的两点, SF 平分 BSD,TF平分 BTD.
BS
①求 的取值范围;
DS
81
②将点S、F 、T 看作一个阿波罗尼斯圆上的三点,若△SFT外接圆的面积为 ,求
8
直线 l的方程.
试卷第 5页,共 5页
参考答案
1.D
【分析】
由题得P { 1,1},再对 P分三种情况讨论得解.
【详解】
由题得P { 1,1},
因为Q Р,所以Q ,{ 1},{1} .
当Q 时, a 0;
当Q { 1}时, a ( 1) 1, a 1 ;
当Q {1}时, a (1) 1, a 1 .
所以实数 a的所有可能取值的集合为 1,0,1 .
故选:D
2.A
【分析】
利用复数的除法运算化简 z,求出 z即可得在复平面内对应的点的坐标以及所在的象限.
【详解】
1 i 1 i 1 2i 1 2i 2z i 3 i 3 1 i
1 2i 1 2i 1 2i 1 4i 2 5 5 5 ,
3 1 3 1z i ,所以
5 5 z
在复平面内对应的点坐标为 , ,
5 5
所以 z在复平面内对应的点位于第一象限,
故选:A.
3.D
【分析】
结合二项式的展开式,求出 x5 的项的系数,根据题意建立方程,解方程即可求出结果.
【详解】
(1 x)n k k k的二项展开式中第 k+1 项为Tk 1 Cn ( 1) x
答案第 1页,共 18页
又因为 (x
1
)(1 1 x)n x(1 x)n (1 x)n的展开式不含
x x x
5 的项
4 4 4 1 6 6 6
所以 xCn ( 1) x Cn ( 1) x 0x
C4x5 C6 5n n x 0
C 4即 n C
6
n
所以 n 10,
故选:D.
4.B
【分析】
结合捆绑法、插空法求得不同的学习方法种数.
【详解】
由题意,知有且仅有三个答题模块相邻,所以从四个答题模块中选三个捆绑在一起,和另外
一个答题模块插空放在两个学习模块的间隙或两端位置,由于“阅读文章”不能放首位,因此
不同的学习方法种数为A3C1 A2 A3 24 2 2 4A3 240 .
故选:B
5.D
【分析】
根据已知条件可得 b 4, a 2, a,b
π
,设OA a 2,0 ,OB b 2,2 3 ,3
uuur r
OC c x, y ,可得点C x, y 的轨迹为圆,由圆的性质即可求解.
【详解】
因为 b 2 a a b 4,所以 b 4, a 2,
cos a,b a b 4 1 π
a b 2 4 2 ,因为
0 a,b π,所以 a,b ,
3
uuur r设OA a 2,0 ,OB b 2,2 3 ,OC c x, y ,
c a x 2, y , c b x 2,2 3 y ,
所以 c a c b x 2 x 2 y 2 3 y 3,
答案第 2页,共 18页
2
即 x2 y 3 4 ,
所以点C x, y 在以M 0, 3 为圆心,半径 r = 2的圆上,
2
c a x 2 2 y 2 表示圆 x2 y 3 4 上的点 x, y 与定点 A 2,0 的距离,
2
所以 c a 2的最小值为 MA r 0 2 3 0 2 7 2 ,
故选:D.
6.B
【分析】
1 2
对 1去分母得 2a b ab,代换 2ab 3a b中的 ab,再结合“1”的妙用即可求解
a b
【详解】
1 2
由 1 2a b ab,则 2ab 3a b 4a 2b 3a b a b,
a b
a b a b 1 2 3 2a b 3 2 2 ,当且仅当 时取到等号,故
a b b a b 2a 2 2
2ab 3a b的最小值为3 2 2 .
故选:B
7.C
【分析】
证明函数 f (x) x sin x
的奇偶性,利用导数得出函数 f (x) 在区间 0, 的单调性,利用单调 2
性解不等式,即可得出答案.
【详解】
f ( x) x sin x x sin x f (x),则函数 f (x) x sin x为偶函数
所以 f (x1) f (x2 ) f ( x1 ) f ( x2 )
当 x 0,
时, f (x) (x sin x)
sin x x cos x 0
2
所以函数 f (x)
在区间 0, 上单调递增 2
2 2
所以 x1 x2 x1 x2
故选:C
【点睛】
答案第 3页,共 18页
本题主要考查了函数的奇偶性以及利用单调性解不等式,属于中档题.
8.A
【分析】
e x
根据给定条件可得 f x 在R 上有最大值,再利用导数探求函数 y x 在R 上的最大值,然e
后结合图象分类讨论即可得解.
【详解】
由题意知,在R 上 f x 有最大值,
y e x e 1 x e x由 x 得: y ,于是得当 x 1时, y 0, y x 在 ,1x 上单调递增,e e e
x 1时, y 0, y
e x
x 在 1, y
e x
上单调递减,因此, x 在R 上有最大值且 ye e max
1,此
时 x 1,
当 a 0时,如上左图, x 1 1,在 ( , a) 上存在 x,使得 f x 1,而在 x a, 时,
f x ≤1,因此, f x 在R 上无最大值,不合题意,
当 a 0 时,如上右图, x 1 1,当 x ( ,a) 时, f x 1,在 x a, 时, f x ≤1,
且 x能取到1,因此, f x 在R 上有最大值1,
所以 a的取值范围是 ( , 0].
故选:A
【点睛】
思路点睛:含参数的分段函数问题,参数值影响式子变形或图形绘制时,往往要分类讨论,
需有明确的标准、全面考虑.
9.AD
【分析】
对于 A、D:直接利用基本不等式进行计算即可;
答案第 4页,共 18页
对于 B、C:利用基本不等式取等号的条件不满足可以判断;
【详解】
1 1 2 1
对于 A:因为 x2 0,所以 f x x2 2 x x 12 2 x 2 2(当且仅当 2 即 时等号x x x
成立).故 A 正确;
对于 B f x x 1 2 x 1: 2取等号的条件为 x 1,但是0 x 1 不能取得.故 B 错误;
x x 2
222 x 3 1对于 C: f x x 4 x2 3 1 2,取等号的条件为 x2 3 1,
x2 3 x2 3 x2 3
此时 x2 2无解,所以选项 C 错误;
4 4 4
对于 D:f x x 2 2 x 2 2,(当且仅当 x 即 x 2时等号成立).故 D 正确;
x x x
故选:AD
【点睛】
易错点睛:利用基本不等式求最值时,要注意其必须满足的三个条件:
(1)“一正二定三相等”“一正”就是各项必须为正数;
(2)“二定”就是要求和的最小值,必须把构成和的二项之积转化成定值;要求积的最大值,则
必须把构成积的因式的和转化成定值;
(3)“三相等”是利用基本不等式求最值时,必须验证等号成立的条件,若不能取等号则这个定
值就不是所求的最值,这也是最容易发生错误的地方.
10.CD
【分析】
根据样本相关系数判断 A 和 B,根据一元线性回归模型的最小二乘估计判断 C 和 D.
【详解】
对于选项 A:当 r 0时,只表明成对样本数据间没有线性相关关系,但是不排除它们之间
有其他相关关系. 故 A 错误;
对于选项 B:样本相关系数 r 越大,成对样本数据的线性相关性越强. 故 B 错误;
对于选项 C:残差和为
n n n n n
yi y i yi bxi a yi b xi a ny nbx na n y bx a 0 . 故 C
i 1 i 1 i 1 i 1 i 1
正确;
对于选项 D:决定系数R2 越大,表示残差平方和越小,即模型的拟合效果越好. 故 D 正确.
答案第 5页,共 18页
故选:CD.
11.ACD
【分析】
A.根据红球数与甲袋中总球数的比求得结果;B.根据黑球数与乙袋中总球数的比求得结果;
C.先利用组合数计算出摸出2个球的总的取法数,再分析摸出2个球都是红球的取法数,根
古典概型的概率计算公式求得结果;D.利用概率的乘法公式求得结果即可.
【详解】
4
对选项 A,从甲袋中随机摸一个球是红球的概率为 P ,故 A 对;
5
2 1
对选项 B,从乙袋中随机摸一个球是黑球的概率为 P ,故 B 错;
6 3
C2
对选项 C,从甲袋中随机摸 2 个球,则 2 个球都是红球的概率 P 4
6 3
C2
,故 C 对;
5 10 5
对选项 D,从甲、乙袋中各随机摸出 1 个球,则这 2 个球是一红球一黑球的概率
P 4 1 1 2 2 ;
5 3 5 3 5
故选:ACD.
12.ABC
【分析】
判断出 f x 周期性、对称性、奇偶性,根据解析式的求法判断 A 选项,结合图象判断 CD
选项.
【详解】
f (x) f (x 4) f x 是周期为 4的周期函数,
f (1 x) f (3 x) f (2 x) f (2 x) f x 的对称轴为 x 2,B 正确.
f (2 x) f (2 x) f 4 x f x ,
则 f x f x , f x 为偶函数.
2 x 4时, x 4, 2 , x 4 0,2 ,
f x f x f x 4 x 4 2 x 4 x2 7x 12 x 3 x 4 ,A 正确.
由此画出 f x 在区间 0,8 的图象如下图所示,
答案第 6页,共 18页
1 2
当0 x 2时, f (x) x2 x x 1 1 2 4
, 2 . 4
结合图象可知 C 正确,D 错误.
故选:ABC
13.0.8185
【分析】
根据正态分布的性质,进行计算概率即可得解.
【详解】
由 X ~ N 68,198 可得 68, 198 14,
P 40 X 82 P 2 X P 2 X 2 P X
2 2
0.9544 0.6826
0.8185 .
2 2
故答案为:0.8185
14. 1 + 6
3
【解析】
【详解】
记∠ = .在 中, = 1, = = 3.故 cos = 3 , sin = 6.
2 3 3
如图,将 绕 旋转,使 在平面 内,此时 在 '处.联结 '、 ' .
则所求的最小值即为 '的长.易知∠ ' = + 30°.故 '2 = 2 + '2 2
'cos∠ '
= 12 + 12 2cos + 30° = 2 2 cos cos30° sin sin30° = 1 + 6.
3
答案第 7页,共 18页
从而, ' = 1 + 6.
3
故答案为: 1 + 6
3
1
15 4.[e , )
4
【分析】
求出函数 f(x)的导数 f x ,再对 f x 求导并根据给定定义列出恒成立的不等式即可得解.
【详解】
ex x ln x m 1因函数 f(x)= x2 ,则 f (x) ex 1 ln x mx, f (x) ex m,
2 x
x 1
依题意, x (1, 4), f (x) 0 e m 0 m ex
1 y ex 1 ,而函数 在(1,4)上单调
x x x
递增,
ex 1 e4 1 4 1即 ,因此,m e ,
x 4 4
1
所以 m 4的取值范围为[e , ) .
4
[e4 1故答案为: , )
4
16.①②④
【分析】
根据题意得到 BN BA得到①正确,计算得到 xN x得到MN∥ y
1
轴,②正确,取 ,
2
5 3 1 1
计算得到 MN 1,③错误, MN y
4 M
yN x 2 2 x
,根据均值不等式得到答案.
【详解】
ON OA 1 OB ,即ON OB OA OB,即 BN BA,故A 、 B、N三点共线,
答案第 8页,共 18页
①正确;
ON OA 1 OB ,OA x1, y1 ,OB x2 , y2 ,故 xN x1 1 x2,
x x1 1 x2 0 1 ,故 xN x,即MN∥ y轴,即直线MN的方向向量可以为
a 0,1 ,②正确;
OB 1,5 1 1 1 1 M 1 5易知OA 0,0 , ,取 ,则 x x1 x ,故 , ,2 2 2 2 2 2 4
1 ON OA 1 1 5 1 5
OB , ,故 N
, MN 5 ,即 1,③错误;2 2 2 2 2 2 4
y x 1 1,2 A 1,0 B 2, 3 y 3 x 3函数 在 上,易知 ( ), ,故直线 AB方程为: .x 2 2 2
MN y y x 1 3 3 3 1 1 3M N x x 2
1 3
2 ,
x 2 2 2 2 x 2 2 2
1
当且仅当 x
1
,即 x 2 时等号成立,故④正确.
2 x
故答案为:①②④.
【点睛】
本题考查了向量共线问题,方向向量,均值不等式求最值,意在考查学生的计算能力和综合
应用能力,其中把向量模长转化为点的纵坐标相减是解题的关键.
17.(1)5;(2)1011.
【分析】
a
(1)用基本量表示 a1,d
2 3
,可得 a1 2d a1 a1 12d ,解得 d 2a1 ,结合 q a 可得解;1
(2)裂项相消法求和,解不等式即得解.
【详解】
(1)设等差数列 an 的公差为 d,由 a1,a3,a13是等比数列 bn 的连续三项,
2
得 a3 a1 a13 ,即 a1 2d
2 a1 a1 12d 2,化简得 4d 8a1d .
d 0, d 2a1.
设数列 bn 的公比的公比为q q
a3 a1 2d a 4a 1 1,则 5a .1 a1 a1
1 1 1 1 1
(2)若 a1 1,则 d 2,an 2n 1, anan 1 (2n 1)(2n 1) 2
2n 1 2n 1
,
答案第 9页,共 18页
S 1 1 1 1 1 n 2 1 3 3 5 5 7 (2 n 1) (2 n 1)
1 1 1 1 1 1 1 1 1 1 1 1 n .2 3 3 5 5 7 2 n 1 2 n 1 2 2 n 1 2 n 1
由 S
1010 n 1010
n ,得 , n 1010 ,故 n的最小值为 1011.2021 2n 1 2021
18.
(1 5)
3
2 3- 5( )
2
【分析】
(1)先由三角形内角和定理、诱导公式、二倍角公式得到关于 sinC的一元二次方程,再利
用同角三角函数基本关系进行求解;
(2)先利用余弦定理和整体思想求得 ab值,再利用三角形的面积公式进行求解.
(1)
解:因为3cos2C 2sin A B 1,
所以3(1 2sin 2 C) 2sin C 1 ,
即6sin2 C+2sinC 4=0,
即3sin2 C+sinC 2=0,
解得 sinC=
2
或 sinC 1(舍),
3
又因为 ABC是锐角三角形,
所以 cosC 1 sin2C 5 .
3
(2)
解:由(1)得: cosC 1 sin2C 5 ,
3
由c 1,a b 5 和余弦定理,得:
a b 5
,
a2 b2
2 5
ab 1
3
则 (a b)2 (a 2 b2 2 5 ab) 4
3
答案第 10页,共 18页
6 3(3 5)
解得 ab = ,
3+ 5 2
所以 ABC的面积公式为
S 1 ab sinC 1 3(3 5) 2 3 5 .
2 2 2 3 2
19.
(1)证明见解析
2 7( )
7
【分析】
(1)取 AD的中点 G,连接 FG、CG,根据平面几何知识证得四边形 BCGE 是平行四边形,
有BF //CG,由线面平行的判定可得证;
(2)以 O为坐标原点, OC所在的直线为 x轴,以OD,OA的方向分别为 y,z轴的正方
向,建立如图所示的空间直角坐标系 O-xyz,由二面角的空间向量求解方法可求得答案.
(1)
1
证明:取 ED的中点 G,连接 FG、CG,因为点 F是 AE的中点,所以 FG //ED,FG ED,
2
又 AD//BC,过点 B作 BE AD且 AE ED 2BC 2BE,所以 BC //ED,BC
1
ED,,
2
所以 FG //BC,FG BC,所以四边形 BCGE 是平行四边形,所以 BF //CG,又 BF 面 ACD,
CG 面 ACD,所以BF // 面 ACD .
(2)
解:取 BD的中点O,连接 CO、AO,因为 BE ED,BE AE,ED AE E,所以BE 面 AED,
又CO//EB,所以CO 面 AED,
又 AED 60 , AE ED,所以 AED是正三角形, AO ED,
所以以 O为坐标原点, OC所在的直线为 x轴,以OD,OA的方向分别为 y,z轴的正方向,
建立如图所示的空间直角坐标系 O-xyz.
设 BC 1,则B 1, 1,0 ,C 1,0,0 ,D 0,1,0 ,A 0,0, 3 ,E 0, 1,0 ,从而 AC 1,0, 3 ,
答案第 11页,共 18页
AD 0,1, 3 , AE 0, 1, 3 , AB 1, 1, 3 .
设平面 ACD的法向量为 n x1, y1, z1 ,
n·AC x1 3z1 0,
则 令 z1 1,得 n 3, 3,1 .
n·AD y1 3z1 0,
设平面 AEB的法向量为m x2 , y2 ,z2 ,
m ·AE y2 + 3z2 0,
则 令 z2 1,得m 0, 3,1 .
m·AB x2 y2 3z2 0,
设平面 ABE与平面 ACD所成的锐二面角为 ,
n m 0 3 1
故 cos cos n, m
7
,所以平面 ABE与平面 ACD所成的锐二面角
n m 7 2 7
7
的余弦值为 .
7
5 2
20.(1)分布列答案见解析,数学期望: ;(2)理论上至少要进行 27 轮游戏,p1 p2 .3 3
【分析】
(1)确定 的所有可能取值并计算相应的概率,即可列出分布列,再根据期望公式求 E 即
可;
(2)求出他们在一轮游戏中获“最佳拍档”的概率 P并化简,再由 0 p1 1,0 p2 1,
p 41 p2 ,求出 p1p2 的取值范围,再利用换元法并结合二次函数的性质即可求出 P3 max
,从
而可得n的最小值及此时 p1, p2 的值.
【详解】
解:(1)两人丢圈套中的次数值和为 ,则 的值可能为 0,1,2,3,4,
答案第 12页,共 18页
2 2
P 0 1 1 1 1 1
3 2
,
9
1 2 1 2 2P 1 C 1 1 1 1 1 C 1 1 12 1 ,
3 3 2 3 2 2 2 3
2 2
P 1 1 1 2 1 1 1
2 1 2 13
2 1 C1 C1 3 2 2 1 1
,
3 3 2 2 2 3 2 36
2 2
P 3 1 C 1 1 1 1 C 1 1 2 1 1 3 2 2 2 2
,
3 3 2 6
2 2
P 4 1 1 1 ,
3 2 36
分布列如下表:
0 1 2 3 4
p 1 1 13 1 1
9 3 36 6 36
E 0 1 1 1 13 1 1 5 2 3 4 .
9 3 36 6 36 3
(2)他们在一轮游戏中获“最佳拍档”的概率为
P C12p 1 p C 2 p
2 C 2 p 2C1p 1 p C 2 p 2 2 2 2 21 1 2 2 2 1 2 2 2 2 1 C2 p2 2p1p2 p 1 p2 3 p 1 p 2
,
p p 4 8 2 2因为 1 2 ,所以P p1p2 3 p1 p2 ,3 3
4 1 1
因为 0 p1 1,0 p2 1, p1 p2 ,所以 p1 1, p3 3 3 1
1,
1 2
所以 p1p
4
2 ,令 t p p
1 t 4 P h t 3t 2 8t 3 t 4 161 2,以 ,则 ,9 9 9 9 3 9 27
4 16
当 t 时, P
9 max
,
27
他们小组在n轮游戏中获“最佳拍档”次数 满足 ~ B n, p ,
由 np 16max ,则 n 27,所以理论上至少要进行 27 轮游戏,
此时 p1 p
4 4 2
2 , p1p2 , p p .3 9 1 2 3
答案第 13页,共 18页
1
21.(1)答案见解析;(2) 1 ln2,
.
2
【分析】
(1)求导,分别讨论m 0和m 0两种情况 f x 的正负,即可求得 y f x 的单调区间.
x
(2)所求转化为求 2m 4 x 2 e lnx x在 x 0,2 恒成立问题,设
g x x 2 ex lnx x,利用导数判断其单调性,并求得 g(x)的最大值,可得关于 m的不
等式,即可得答案.
【详解】
1 1 mx
(1) f x m , (x 0).
x x
当m 0时, f x 0,所以 y f x 在 0, 为增函数,
1
当m 0时,令 f (x) 0,解得 x ;
m
x 0, 1 当 时, f x 0, y f x 为增函数,
m
x 1 , 当 时, f x 0, y f x 为减函数,
m
综上:当m 0时, y f x 的单调增区间为 0, ,
1 1
当m 0时, y f x 的单调增区间为 0, ,单调减区间为 , .
m m
(2)因为 f x 2 x e x m 1 在 x 0,2 恒成立,
所以 2m 4 x 2 ex lnx x在 x 0,2 恒成立,
设 g x x 2 ex lnx x g x x 1 ex 1 1 ,则 1 x 1 x
x
e
x
.
设 h x 1 ex ,h x ex 1 0
x x2
所以 h x 在 0,2 1 单调递增,又 h e 2 0,h 1 e 1 0,
2
1
因此存在唯一 x0 ,1 ,使得 h x0 0,
2
所以当 x 0, x0 时, h x 0,
当 x x0 ,1 时, h x 0.
当 x 0, x0 时, g x 0 ,当 x x0 ,1 时, g x 0.
答案第 14页,共 18页
所以函数 g x 在 0, x0 递增,在 x0 ,1 递减,在 1,2 递增
因此 g(x)max max g x0 , g 2 ,
h x e x 1 1由 00 0得 ex0 ,则 lnx0 xx 0 .0 x0
所以 g x0 x 2 ex lnx x
1 1
0
0 0 0 x0 2 2x0 1 2 x0 x x ,0 0
1
因为 x
1
0 ,1
,则 x0 2,所以 g x0 3,
2 x0
因为 g 2 ln2 2 2 ,
所以当 x 0,2 时, g(x)max g 2 ln2 2,
1
所以 2m 4 ln2 2,解得m 1 ln 2
2
所以m 1
1
的取值范围是 ln2,
2
【点睛】
解题的关键是熟练掌握利用导数判断函数单调性,求极(最)值的方法,并灵活应用,在得
到 g x 解析式,并且不能直接判断其正负时,可令 h x g (x) ,再次求导,根据 h x 的
单调性,求得 h x 的值域,进而可得 g x 的正负,即可得 g(x) 的单调性,属中档题.
2 2 1
22 1 x y 1 2 ,1 5 10.( ) = ;( )①
8 6 3
;② y x .
2 2
【分析】
(1)方法 1,利用特殊值法,求得椭圆方程,方法 2,利用定义整理得
x2 y2 2x 2a
2 2x a
2 c 2
0,再根据条件列式求得椭圆方程;方法 3,利用定义进行
2 1 2 1
MF BS BF
整理,由 为常数,求得系数,得到椭圆方程;(2)①首先由面积比值求得 ,
MA DS DF
BF 3
令 ,则 BF FD,利用坐标表示向量,求得 5 2x ,再求范围;②由阿波DF 0
罗尼斯圆定义知,S,T , F 在以 B,D为定点得阿波罗尼斯圆上,由几何关系列式得
答案第 15页,共 18页
BF 2r BF 1 1 2 2x 0 2 2
,求得 r,再根据 BF DF 1 9 ,求得 x0 , y ,即可计DF 2r DF 3 2 2 x
0
2 0
算直线方程.
【详解】
c 2 c 2
(1)方法(1)特殊值法,令M 2,0 , ,且 a 2c,解得 2
a 2 a 2 c 2
2 2
∴ a2 8,b2 a2 c2 6,椭圆C x y的方程为 =18 6
2
MF x c y 2
方法(2)设M x, y ,由题意 (常数),
MA 2x a y 2
x2 y2 2x 2a
2 2x a
2 c 2
整理得: 2 0, 1 2 1
2c 2a 2
0
2 1 c 1
故 ,又 2 ,解得: a 2 2 , c 2 .
a
2 c2 a 2
2 4 1
b2 a2 c2 x
2 y2
∴ 6,椭圆C的方程为 =1.8 6
方法(3)设M x, y ,则 x2 y2 4 .
2 2
MF x c y2 x c 4 x2 c2 4 2cx
由题意
MA 2 2 2x a y2 x a 4 x2 a 4 2ax
MF c2 4 c c 1
∵ 为常数,∴ 2 ,又 ,解得: a
2 8,c2 2,故MA a 2 b
2 a2 c2 6
a 4 a
2 2
∴椭圆C x y的方程为 =1
8 6
1
S SB SF sin BSF SB BF
(2)①由 SBF 2
S
1 ,又
SBF ,
S SDF SD SF sin DSF SD S SDF DF
2
BS BF
∴ (或由角平分线定理得)
DS DF
BF
令 2 2,则 BF FD,设D x0 , y0 ,则有3x 4y 24 ,DF 0 0
答案第 16页,共 18页
xB 2 1 x又直线 l的斜率 k 0,则 x0 2 2, 2 0, 代入3x2 4y2 24 0 得:
yB y0
2
3 2 1 x 4 20 y 20 24 0,即 1 5 3 2 x 0 0,
∵ 0,∴
3 1
,1 .
5 2x 0 3
SB TB BF
②由①知, ,由阿波罗尼斯圆定义知,
SD TD DF
S,T , F 在以 B,D为定点得阿波罗尼斯圆上,设该圆圆心为C1,半径为 r,与直线 l的
另一个交点为 N,
BF NB BF 2r 1 BF r
则有 ,即 ,解得: 1 1 .
DF ND DF 2r DF BF DF
9 1 1 2 2
又 S圆C r
2 81 ,故 r ,∴
1 8 2 2 BF DF 9
又 DF 2 2x 2 y 2 3 10 0 x 20 2 6 x4 0 2 2 x0 ,2
1 1 1 1 5 2x0 1 2 2x 2 2 0
∴ BF DF DF DF 1 ,3 2 2 1 x 1 0 2 2 x2 0 3 2 2 x
9
2 2 0
3 3 10
解得: x 20 , y0 6 x
2
0 ,2 4 4
y 5 5 10
∴ k 0 ,∴直线 l的方程为 y x .
2 x0 2 2 2
【点睛】
答案第 17页,共 18页
关键点点睛:本题考查轨迹问题,考查直线与椭圆的位置关系,以及外接圆,新定义的综合
应用,属于难题,本题的关键是读懂题意,并根据几何关系进行消参,转化与化归,是本题
的关键也是难点.
答案第 18页,共 18页
同课章节目录
