2021-2022学年高二上学期数学人教A版(2019)选择性必修第二册4.2.1等差数列的概念能力提升练word版含答案
文档属性
| 名称 | 2021-2022学年高二上学期数学人教A版(2019)选择性必修第二册4.2.1等差数列的概念能力提升练word版含答案 |  | |
| 格式 | docx | ||
| 文件大小 | 735.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-06 15:50:26 | ||
图片预览



文档简介
等差数列的概念能力提升练
题组一 等差数列的通项公式及其应用
1.在数列中,,且对任意大于1的正整数,点,在函数的图象上,则
A. B. C. D.
2.已知等差数列首项为,公差为1,,若对任意的正整数都有,则实数的取值范围是
A.,, B.
C.,, D.
3.已知数列满足:,,.
(1)证明:数列为等差数列,
(2)并求出数列的通项公式
题组二等差数列的性质及其应用
1.一个首项为23,公差为整数的等差数列,如果前六项均为正数,第七项起为负数,则它的公差是
A. B. C. D.
2.已知数列是等差数列,若,,则公差
A.1 B. C. D.
3.已知各项都为正数的等差数列中,,则的最大值为 .
4.中,角,,所对的边长分别为,,.若,,成等差数列,则的最小值为 .
题组三 等差数列的综合应用
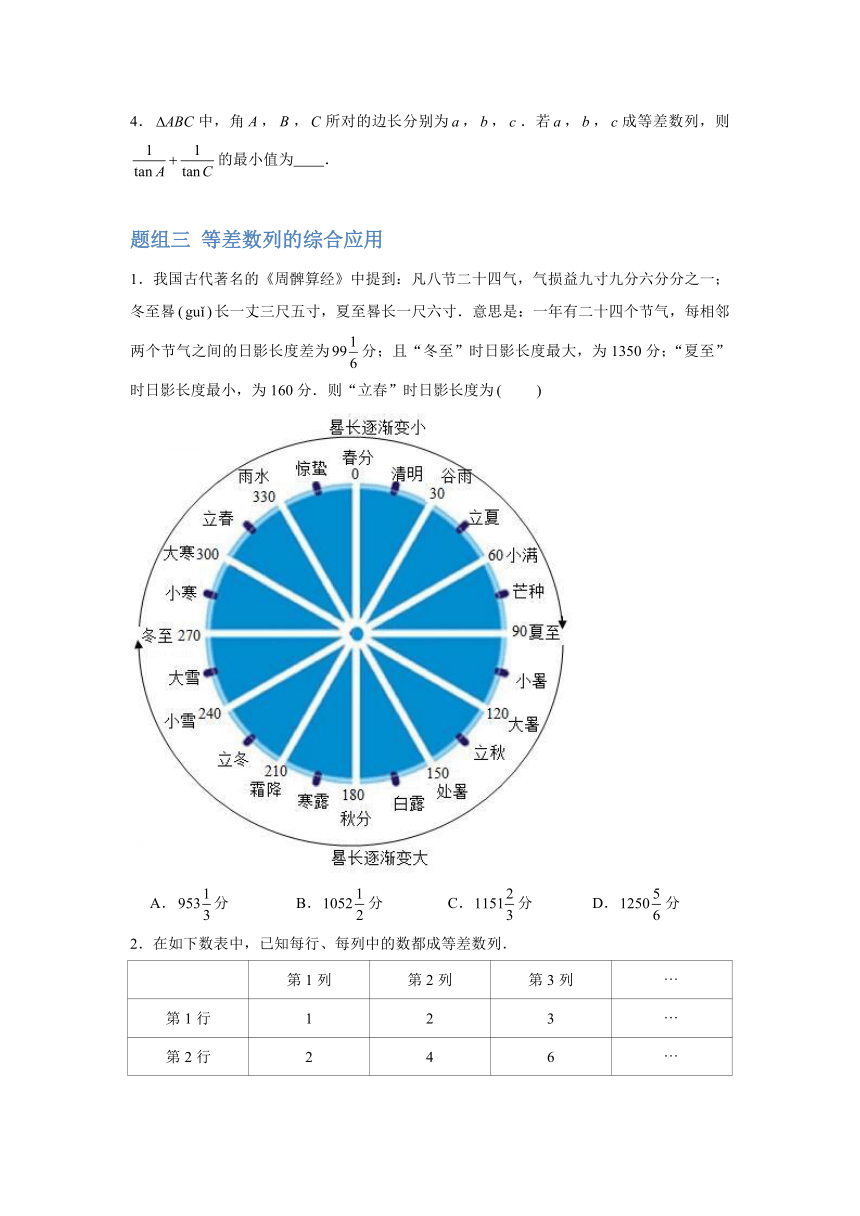
1.我国古代著名的《周髀算经》中提到:凡八节二十四气,气损益九寸九分六分分之一;冬至晷guǐ长一丈三尺五寸,夏至晷长一尺六寸.意思是:一年有二十四个节气,每相邻两个节气之间的日影长度差为分;且“冬至”时日影长度最大,为1350分;“夏至”时日影长度最小,为160分.则“立春”时日影长度为
A.分 B.分 C.分 D.分
2.在如下数表中,已知每行、每列中的数都成等差数列.
第1列 第2列 第3列
第1行 1 2 3
第2行 2 4 6
第3行 3 6 9
那么位于表中的第行第列的数是
A. B. C. D.
3.已知数列满足,且,若,则正整数 .
4.已知正项数列满足.
(1)求证:数列是等差数列;
(2)若数列满足,且数列的最大项为,最小项为,求的值.
5.数列中,在,.
(1)求数列的通项公式;
(2)若对任意的,恒成立,求实数的取值范围.
6.已知无穷等差数列,首项,公差,依次取出项的序号被4除余3的项组成数列
(1)求和;
(2)求的通项公式;
(3)中的第110项是中的第几项?
答案解析
题组一
1.【解答】解:在数列中,,且对任意大于1的正整数,点,在函数的图象上,
可得,
所以数列是以为首项,为公差的等差数列,
所以,
所以.
故选:.
2.【解答】解:等差数列首项为,公差为1,
所以,
所以,
则,
若对任意的正整数都有,
所以,
所以,
解得.
故选:.
3.【解答】解:(1)证明:由,,,
可得数列是首项为,公差为的等差数列,
则,即有;
题组二
1.【解答】解:设等差数列的公差为,
所以,,
又因为数列前六项均为正数,第七项起为负数,
所以,
因为数列是公差为整数的等差数列,
所以.
故选:.
2.【解答】解:由是等差数列,得,解得,
又,解得,
公差.
故选:.
二.填空题(共2小题)
3.【解答】解:依题意,等差数列各项都为正数,
所以,,
所以.
当且仅当时等号成立.
故答案为:9.
4.【解答】解:,,成等差数列,.
则,
,
,,则,
即,.
即.
.
当且仅当时,上式等号成立.
的最小值为.
故答案为:.
题组三
1.【解答】解:一年有二十四个节气,每相邻两个节气之间的日影长度差为分,
且“冬至”时日影长度最大,为1350分;“夏至”时日影长度最小,为160分.
,
解得,
“立春”时日影长度为:(分.
故选:.
2.【解答】解:由题意可得:,.
故选:.
二.填空题(共1小题)
3.【解答】解:数列满足,且,整理得(常数),
所以数列是以为首项,为公差的等差数列.
则,
由于,则,
解得,
所以正整数.
故答案为:23.
三.解答题(共3小题)
4.【解答】(1)证明:由,
得,且,
得,.
,
由,解得.
数列是以首项为2,公差为2的等差数列;
(2)解:,
当时,最大,当时,最小,
.
5.【解答】解:(1)由,得,
又,即,数列是以1为首项,以3为公差的等差数列,
则,可得;
(2)对任意的,恒成立,
即对任意的,恒成立,
对任意的,恒成立,
令,则.
当时,,即.
.
故实数的取值范围是,.
6.【解答】解:(1)由题意,等差数列的通项公式为,
令取出项为,则需满足,
,
.
(2)取出的序号成等差数列,
所对应的项组成的新数列也为等差数列,且首项为,公差为,
.
(3),
当时,
项,
中的第110项是中的第439项
题组一 等差数列的通项公式及其应用
1.在数列中,,且对任意大于1的正整数,点,在函数的图象上,则
A. B. C. D.
2.已知等差数列首项为,公差为1,,若对任意的正整数都有,则实数的取值范围是
A.,, B.
C.,, D.
3.已知数列满足:,,.
(1)证明:数列为等差数列,
(2)并求出数列的通项公式
题组二等差数列的性质及其应用
1.一个首项为23,公差为整数的等差数列,如果前六项均为正数,第七项起为负数,则它的公差是
A. B. C. D.
2.已知数列是等差数列,若,,则公差
A.1 B. C. D.
3.已知各项都为正数的等差数列中,,则的最大值为 .
4.中,角,,所对的边长分别为,,.若,,成等差数列,则的最小值为 .
题组三 等差数列的综合应用
1.我国古代著名的《周髀算经》中提到:凡八节二十四气,气损益九寸九分六分分之一;冬至晷guǐ长一丈三尺五寸,夏至晷长一尺六寸.意思是:一年有二十四个节气,每相邻两个节气之间的日影长度差为分;且“冬至”时日影长度最大,为1350分;“夏至”时日影长度最小,为160分.则“立春”时日影长度为
A.分 B.分 C.分 D.分
2.在如下数表中,已知每行、每列中的数都成等差数列.
第1列 第2列 第3列
第1行 1 2 3
第2行 2 4 6
第3行 3 6 9
那么位于表中的第行第列的数是
A. B. C. D.
3.已知数列满足,且,若,则正整数 .
4.已知正项数列满足.
(1)求证:数列是等差数列;
(2)若数列满足,且数列的最大项为,最小项为,求的值.
5.数列中,在,.
(1)求数列的通项公式;
(2)若对任意的,恒成立,求实数的取值范围.
6.已知无穷等差数列,首项,公差,依次取出项的序号被4除余3的项组成数列
(1)求和;
(2)求的通项公式;
(3)中的第110项是中的第几项?
答案解析
题组一
1.【解答】解:在数列中,,且对任意大于1的正整数,点,在函数的图象上,
可得,
所以数列是以为首项,为公差的等差数列,
所以,
所以.
故选:.
2.【解答】解:等差数列首项为,公差为1,
所以,
所以,
则,
若对任意的正整数都有,
所以,
所以,
解得.
故选:.
3.【解答】解:(1)证明:由,,,
可得数列是首项为,公差为的等差数列,
则,即有;
题组二
1.【解答】解:设等差数列的公差为,
所以,,
又因为数列前六项均为正数,第七项起为负数,
所以,
因为数列是公差为整数的等差数列,
所以.
故选:.
2.【解答】解:由是等差数列,得,解得,
又,解得,
公差.
故选:.
二.填空题(共2小题)
3.【解答】解:依题意,等差数列各项都为正数,
所以,,
所以.
当且仅当时等号成立.
故答案为:9.
4.【解答】解:,,成等差数列,.
则,
,
,,则,
即,.
即.
.
当且仅当时,上式等号成立.
的最小值为.
故答案为:.
题组三
1.【解答】解:一年有二十四个节气,每相邻两个节气之间的日影长度差为分,
且“冬至”时日影长度最大,为1350分;“夏至”时日影长度最小,为160分.
,
解得,
“立春”时日影长度为:(分.
故选:.
2.【解答】解:由题意可得:,.
故选:.
二.填空题(共1小题)
3.【解答】解:数列满足,且,整理得(常数),
所以数列是以为首项,为公差的等差数列.
则,
由于,则,
解得,
所以正整数.
故答案为:23.
三.解答题(共3小题)
4.【解答】(1)证明:由,
得,且,
得,.
,
由,解得.
数列是以首项为2,公差为2的等差数列;
(2)解:,
当时,最大,当时,最小,
.
5.【解答】解:(1)由,得,
又,即,数列是以1为首项,以3为公差的等差数列,
则,可得;
(2)对任意的,恒成立,
即对任意的,恒成立,
对任意的,恒成立,
令,则.
当时,,即.
.
故实数的取值范围是,.
6.【解答】解:(1)由题意,等差数列的通项公式为,
令取出项为,则需满足,
,
.
(2)取出的序号成等差数列,
所对应的项组成的新数列也为等差数列,且首项为,公差为,
.
(3),
当时,
项,
中的第110项是中的第439项
