2021-2022学年高二上学期数学人教A版(2019)选择性必修第一册3.2 双曲线方程及其几何性质 综合提升(word版含答案))
文档属性
| 名称 | 2021-2022学年高二上学期数学人教A版(2019)选择性必修第一册3.2 双曲线方程及其几何性质 综合提升(word版含答案)) |  | |
| 格式 | docx | ||
| 文件大小 | 293.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-06 15:51:27 | ||
图片预览




文档简介
专题 双曲线
双曲线及其标准方程
知识点一 双曲线的定义
1.定义:平面内与两个定点F1,F2的距离的差的绝对值等于非零常数(小于|F1F2|)的点的轨迹.
2.定义的集合表示:{M|||MF1|-|MF2||=2a,0<2a<|F1F2|}.
3.焦点:两个定点F1,F2.
4.焦距: 两焦点间 的距离,表示为|F1F2|.
注意: (1)当2a<|F1F2|时,P点的轨迹是双曲线.
(2)当2a=|F1F2|时,P点的轨迹是两条射线.
(3)当2a>|F1F2|时,P点不存在.
例题1:在平面直角坐标系xOy中,已知点F1(﹣5,0),F2(5,0),动点P满足|PF1|﹣|PF2|=8,则点P的轨迹是( )
A.椭圆 B.双曲线
C.双曲线的左支 D.双曲线的右支
变式1:平面内到两定点F1(﹣3,0)、F2(3,0)的距离之差的绝对值等于4的点M的轨迹( )
A.椭圆 B.线段 C.两条射线 D.双曲线
知识点二 双曲线标准方程
焦点位置 焦点在x轴上 焦点在y轴上
图形
标准方程 -=1(a>0,b>0) -=1(a>0,b>0)
焦点 (-c,0),(c,0) (0,-c),(0,c)
a,b,c的关系 c2=a2+b2
例题2:(1)已知双曲线-=1(a>0,b>0)的左、右焦点分别为F1,F2,点P在双曲线的右支上,若|PF1|-|PF2|=b,且双曲线的焦距为2,则该双曲线的方程为__________.
(2) “m<3”是“方程+=1表示双曲线”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
(3)求满足下列条件的双曲线的标准方程:
(Ⅰ)c=5,b=3,焦点在x轴上;
(Ⅱ)a=2,经过点A(2,﹣5),焦点在y轴上.
(Ⅲ)经过两点(3,0),(﹣6,﹣3);
变式2:(1)设动点P到A(-5,0)的距离与它到B(5,0)距离的差等于6,则P点的轨迹方程是( )
A.-=1 B.-=1
C.-=1(x≤-3) D.-=1(x≥3)
(2)命题p:“3<m<4”是命题q:“曲线=1表示双曲线”的( )
A.充要条件 B.必要不充分条件
C.充分不必要条件 D.既不充分也不必要条件
(3)求适合下列条件的双曲线的标准方程:
(Ⅰ)求实轴长为2,焦距为4的双曲线的标准方程;
(Ⅱ),经过点(﹣5,2),焦点在x轴上.
(Ⅲ)求以A(﹣3,0)为一个焦点,实轴长为的双曲线的标准方程.
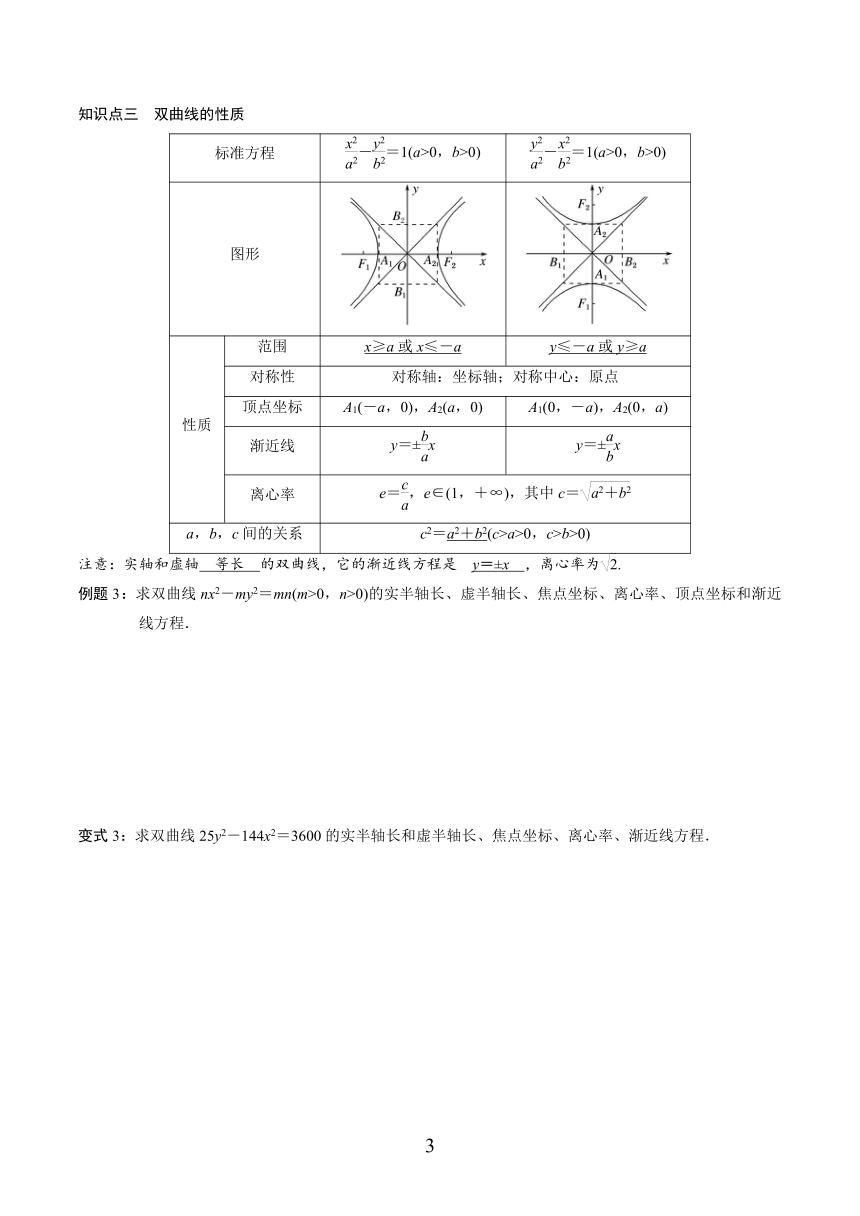
知识点三 双曲线的性质
标准方程 -=1(a>0,b>0) -=1(a>0,b>0)
图形
性质 范围 x≥a或x≤-a y≤-a或y≥a
对称性 对称轴:坐标轴;对称中心:原点
顶点坐标 A1(-a,0),A2(a,0) A1(0,-a),A2(0,a)
渐近线 y=±x y=±x
离心率 e=,e∈(1,+∞),其中c=
a,b,c间的关系 c2=a2+b2(c>a>0,c>b>0)
注意:实轴和虚轴 等长 的双曲线,它的渐近线方程是 y=±x ,离心率为.
例题3:求双曲线nx2-my2=mn(m>0,n>0)的实半轴长、虚半轴长、焦点坐标、离心率、顶点坐标和渐近线方程.
变式3:求双曲线25y2-144x2=3600的实半轴长和虚半轴长、焦点坐标、离心率、渐近线方程.
重难点
重点一、双曲线方程问题
巧设双曲线方程
(1)与双曲线-=1(a>0,b>0)有共同渐近线的方程可表示为-=λ(λ≠0).
(2)过已知两个点的双曲线方程可设为mx2﹣ny2=1(mn>0).
例题4:求下列双曲线方程
(1)已知双曲线过点(3,﹣2)和点(,1);
(2)已知双曲线C过点(,-1),且与双曲线=1有相同的渐近线.
变式4:求满足下列条件的双曲线方程
(1)已知双曲线经过两点A(,), B(,);
(2)已知双曲线C过点M(2,2),且与x2﹣4y2=4有相同的渐近线.
重点二、双曲线渐近线与离心率问题
例题5:(1)已知曲线C:=1(a>0,b>0)其中一条渐近线与直线l:x+2y=2平行,则此双曲线的离心率是( )
A. B. C. D.
(2)已知双曲线C:=1(a>0,b>0)的左、右焦点分别为F1,F2,以|F1F2|为直径的圆交双曲线的右支于点P,若∠PF1F2=30°,则双曲线C的离心率为( )
A. B. C. D.
变式5:若点M(4,0)到双曲线C:=1(b>0)的一条渐近线的距离为2,则双曲线C的离心率为( )
A.2 B. C. D.
(2)已知双曲线=1(a>0,b>0)的左、右焦点分别为F1,F2,双曲线上有一点A,若|F1F2|=10,|AF1|+|AF2|=14,且AF1⊥AF2,则双曲线的渐近线方程为( )
A.y=±5x B.y=x C.y=x D.y=x
课堂反馈
一.选择题(共5小题)
1.已知M(﹣2,0),N(2,0),|PM|﹣|PN|=4,则动点P的轨迹是( )
A.一条射线 B.双曲线 C.双曲线左支 D.双曲线右支
2.“n>m>0”是“方程=1表示焦点在y轴上的双曲线”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.既不充分也不必要条件
3.双曲线C:=1(m>0)的一条渐近线的方程为2x+y=0,则双曲线C的离心率为( )
A. B.2 C.4 D.
4.椭圆C1:=1与双曲线C2:=1(a>0,b>0)的离心率之积为1,则双曲线的渐近线方程为( )
A.y=±2x B.y=x C.y=±x D.y=x
5.已知双曲线=1(a>0,b>0)的左、右焦点分别为F1,F2,双曲线上有一点A,若|F1F2|=10,|AF1|+|AF2|=14,且AF1⊥AF2,则双曲线的渐近线方程为( )
A.y=±5x B.y=±2x C.y=±x D.y=±2x
二.多选题(共4小题)
6.双曲C1:=1与C2:=λ(λ>0且λ≠1)的( )
A.顶点相同 B.焦点相同 C.离心率相同 D.渐近线相同
7.已知双曲线C:=1,下列对双曲线C的判断正确的是( )
A.实轴长是虚轴长的2倍 B.焦距为4
C.离心率为 D.渐近线方程为x±y=0
8.已知中心在原点,焦点在坐标轴上的双曲线C与椭圆=1有相同的焦距,且一条渐近线方程为
x﹣2y=0,则双曲线C的方程可能为( )
A.=1 B.=1 C.=1 D.=1
9.若双曲线C的一个焦点为F(5,0),P是双曲线上一点,且渐近线方程为y=x,则下列结论正确的是( )
A.C的方程为=1 B.C的离心率为
C.焦点到渐近线的距离为3 D.|PF|的最小值为2
三.填空题(共5小题)
10.若双曲线=1的焦点与椭圆=1的焦点相同,则实数t= .
11.已知双曲线C1:=1,与C1共渐近线的双曲线C2过(2,4),则C2的方程是 .
12.已知双曲线=1的焦点为F1,F2,过右焦点F2的直线交双曲线右支于A、B两点,
若|AF1|+|BF1|=2|AB|,则|AB|等于 .
13.已知双曲线E:=1(b>0)的渐近线方程为y=±x,则双曲线E的焦距等于 .
14.双曲线=1的右焦点到渐近线的距离为 .
四.解答题(共2小题)
15.根据下列条件,求双曲线的标准方程.
(1)与双曲线=1有公共焦点,且经过点(4,3);
(2)焦点为(0,±5),且渐近线方程为y=±2x.
16.设F1、F2是双曲线=1的左、右焦点,点P在该双曲线上,且PF1⊥PF2,求△PF1F2的面积.
声明:试题解析著作权属所有,未经书面同意,不得复制发布
日期:2021/12/1 19:56:43;用户:高中数学;邮箱:gzsxx@;学号:29081547
答案解析
例题1:在平面直角坐标系xOy中,已知点F1(﹣5,0),F2(5,0),动点P满足|PF1|﹣|PF2|=8,则点P的轨迹是( )
A.椭圆 B.双曲线
C.双曲线的左支 D.双曲线的右支
【解答】解:由于两点间的距离|F1F2|=10,动点P满足|PF1|﹣|PF2|=8<10,
所以满足条件|PF1|﹣|PF2|=8的点P的轨迹是双曲线中离F2较近的一支.
故选:D.
变式1:平面内到两定点F1(﹣3,0)、F2(3,0)的距离之差的绝对值等于4的点M的轨迹( )
A.椭圆 B.线段 C.两条射线 D.双曲线
【解答】解:根据双曲线的定义,
|MF1|﹣|MF2|=±4,
且|F1F2|=6>4,
∴点M的轨迹是焦点在x轴上的双曲线,且焦距为6.
故选:D.
例题2:(1)已知双曲线-=1(a>0,b>0)的左、右焦点分别为F1,F2,点P在双曲线的右支上,若|PF1|-|PF2|=b,且双曲线的焦距为2,则该双曲线的方程为__________.
(2) “m<3”是“方程+=1表示双曲线”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
【解答】解:当为双曲线时,(m+2)(m﹣3)<0
∴﹣2<m<3,
∵(﹣2,3) (3,+∞)
故选:B.
(3)求满足下列条件的双曲线的标准方程:
(Ⅰ)c=5,b=3,焦点在x轴上;
(Ⅱ),经过点A(2,﹣5),焦点在y轴上.
(Ⅲ)经过两点(3,0),(﹣6,﹣3);
【解答】解:(Ⅰ)∵双曲线的焦点在x轴上,c=5,b=3,
∴a2=c2﹣b2=16,
∴双曲线方程为:;
(Ⅱ)∵双曲线的焦点在y轴上,
∴可设双曲线的标准方程为,
∵由题设知,,且点A(2,﹣5)在双曲线上,
∴
∴解得a2=20,b2=16,
∴所求双曲线的标准方程为.
(Ⅲ)根据题意,若双曲线经过点(3,0),
则双曲线的焦点在x轴上,且a=3,设其标准方程为﹣=1;
又由双曲线经过点(﹣6,﹣3),则有4﹣=1,则b2=3,
则双曲线的标准方程为﹣=1;
变式2:(1)设动点P到A(-5,0)的距离与它到B(5,0)距离的差等于6,则P点的轨迹方程是( )
A.-=1 B.-=1
C.-=1(x≤-3) D.-=1(x≥3)
【解答】由题意知,轨迹应为以A(-5,0),B(5,0)为焦点的双曲线的右支.
由c=5,a=3,知b2=16,
∴P点的轨迹方程为-=1(x≥3).
答案 D
(2)命题p:“3<m<4”是命题q:“曲线表示双曲线”的( )
A.充要条件 B.必要不充分条件
C.充分不必要条件 D.既不充分也不必要条件
【解答】解:3<m<5 曲线表示双曲线,
因为曲线表示双曲线,
所以(m﹣3)(5﹣m)>0,解得3<m<5,
∴命题p:“3<m<4”是命题q:“曲线表示双曲线”的充分不必要条件.
故选:C.
(3)求适合下列条件的双曲线的标准方程:
(Ⅰ)(Ⅰ)求实轴长为2,焦距为4的双曲线的标准方程;
(Ⅱ),经过点(﹣5,2),焦点在x轴上.
(Ⅲ)求以A(﹣3,0)为一个焦点,实轴长为的双曲线的标准方程.
【解答】解:(Ⅰ)根据题意,要求椭圆的实轴长为2,焦距为4,即2a=2,2c=4,
则a=1,c=2,则b==;
若要求椭圆的焦点在x轴上,则其标准方程为x2-=1,
若要求椭圆的焦点在y轴上,则其标准方程为y2-=1,
故要求椭圆的标准方程为x2-=1或y2-=1;
(Ⅱ)∵焦点在x轴上,,
∴设所求双曲线方程为:(其中0<λ<6)
∵双曲线经过点(﹣5,2),∴
∴λ=5或λ=30(舍去)
∴所求双曲线方程是
(Ⅲ)要求双曲线以A(﹣3,0)为一个焦点,实轴长为,
则其焦点在x轴上,且c=3,2a=2,即a=,
则b==2,
则要求双曲线的标准方程为.
例题3:求双曲线nx2-my2=mn(m>0,n>0)的实半轴长、虚半轴长、焦点坐标、离心率、顶点坐标和渐近线方程.
【解答】把方程nx2-my2=mn(m>0,n>0)化为标准方程为-=1(m>0,n>0),
由此可知,实半轴长a=,
虚半轴长b=,c=,
焦点坐标为(,0),(-,0),
离心率e===,
顶点坐标为(-,0),(,0),
所以渐近线方程为y=± x,即y=±x.
变式3:求双曲线25y2-144x2=3600的实半轴长和虚半轴长、焦点坐标、离心率、渐近线方程.
解 把方程25y2-144x2=3600化为标准方程为.
由此可知,实半轴长a=12,虚半轴长b=5;
c===13,焦点坐标是(0,-13),(0,13);
离心率e==;渐近线方程为y=x.
例题4:求下列双曲线方程
(1)已知双曲线过点(3,﹣2)和点;
已知双曲线C过点,且与双曲线=1有相同的渐近线.
【解答】解:(1)若双曲线焦点在x轴上,设双曲线C的标准方程为:mx2﹣ny2=1(mn>0),
则,解得m,n,
∴双曲线C的标准方程是:.
(2)设与双曲线=1有相同的渐近线的双曲线C的方程为:﹣=λ,
由双曲线C过点(2,﹣1)可得:﹣=λ,解得λ=,
所以双曲线C的标准方程:﹣=1;
故答案为:﹣=1.
变式4:求满足下列条件的双曲线方程
(1)已知双曲线经过两点,;
(2)已知双曲线C过点M(2,2),且与x2﹣4y2=4有相同的渐近线.
【解答】(1)解:设双曲线的方程为nx2﹣my2=1,mn>0,
把两点,代入,得:,
解得n=1,m=,
∴所求的双曲线方程为x2﹣=1,c=,
双曲线的焦距为:.
(2)解:设与x2﹣4y2=4有相同的渐近线的双曲线方程为与x2﹣4y2=4λ(λ≠0),
代入点M(2,2),得22﹣4×22=4λ,即λ=﹣3.
∴双曲线C的方程为.
故答案为:.
例题5:(1)已知曲线其中一条渐近线与直线l:x+2y=2平行,则此双曲线的离心率是( )
A. B. C. D.
【解答】解:根据题意,双曲线C的方程为(a>0,b>0),
则其渐近线方程为y=±x,
又由其一条渐近线与直线l:x+2y=2平行,有=,即b=a,
则c==a=a,
则其离心率e==,
故选:B.
(2)已知双曲线C:=1(a>0,b>0)的左、右焦点分别为F1,F2,以|F1F2|为直径的圆交双曲线的右支于点P,若∠PF1F2=30°,则双曲线C的离心率为( )
A. B. C. D.
【解答】解:设|F1F2|=2c,
由于P是以F1F2为直径的圆与该双曲线的一个交点
则△F1F2P是直角三角形,∠F1PF2=90°,
由∠PF1F2=30°,
∴|PF1|=c,|PF2|=c,
∴|PF1|﹣|PF2|=c﹣c=2a,
∴e===.
故选:D.
变式5:若点M(4,0)到双曲线C:=1(b>0)的一条渐近线的距离为2,则双曲线C的离心率为( )
A.2 B. C. D.
【解答】解:由双曲线的对称性,M到任意一条渐近线的距离相等,
由双曲线的方程可得渐近线的方程:y=±x,
即bx±3y=0,
所以M到渐近线的距离d=,
所以2=,b>0,
可得:b2=3,
所以双曲线的离心率e====,
故选:D.
(2)已知双曲线的左、右焦点分别为F1,F2,双曲线上有一点A,若|F1F2|=10,|AF1|+|AF2|=14,且AF1⊥AF2,则双曲线的渐近线方程为( )
A.y=±5x B. C. D.
【解答】解:设|AF1|=m,|AF2|=n,,由|AF1|+|AF2|=14,得m+n=14,
又AF1⊥AF2,所以m2+n2=102,
解方程组,得m=8,n=6或m=6,n=8;
所以||AF1|﹣|AF2||=2=2a,所以a=1,
又|F1F2|=10,所以c=5,
所以b==2,
双曲线的渐近线方程为y=±2x,
故选:B.
课堂反馈
一.选择题(共5小题)
1.已知M(﹣2,0),N(2,0),|PM|﹣|PN|=4,则动点P的轨迹是( )
A.一条射线 B.双曲线 C.双曲线左支 D.双曲线右支
【解答】解:如果是双曲线,那么|PM|﹣|PN|=4=2a
a=2
而两个定点M(﹣2,0),N(2,0)为双曲线的焦点
c=2
而在双曲线中c>a
所以把后三个关于双曲线的答案全部排除,
故选:A.
2.“n>m>0”是“方程表示焦点在y轴上的双曲线”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.既不充分也不必要条件
【解答】解:若n>m>0,则方程表示焦点在y轴上的双曲线,
若方程表示焦点在y轴上的双曲线,则n>0且m>0,
所以“n>m>0”是“方程表示焦点在y轴上的双曲线”充分不必要条件.
故选:A.
3.双曲线C:=1(m>0)的一条渐近线的方程为2x+y=0,则双曲线C的离心率为( )
A. B.2 C.4 D.
【解答】解:根据题意,双曲线C:=1(m>0)的一条渐近线的方程为2x+y=0,
则有,即m=8,
则双曲线的方程为双曲线:=1,
其中a=,b=2,则c=,
则双曲线的离心率e==.
故选:D.
4.椭圆C1:=1与双曲线C2:=1(a>0,b>0)的离心率之积为1,则双曲线的渐近线方程为( )
A.y=±2x B. C. D.
【解答】解:设椭圆的离心率为e1,则e1=,
双曲线的离心率为e2,
由题意可得e1e2== =1,
可得=,
由双曲线C2的渐近线方程为y=±x,即y=±x,
故选:D.
5.已知双曲线的左、右焦点分别为F1,F2,双曲线上有一点A,若|F1F2|=10,|AF1|+|AF2|=14,且AF1⊥AF2,则双曲线的渐近线方程为( )
A.y=±5x B. C. D.
【解答】解:设|AF1|=m,|AF2|=n,,由|AF1|+|AF2|=14,得m+n=14,
又AF1⊥AF2,所以m2+n2=102,
解方程组,得m=8,n=6或m=6,n=8;
所以||AF1|﹣|AF2||=2=2a,所以a=1,
又|F1F2|=10,所以c=5,
所以b==2,
双曲线的渐近线方程为y=±2x,
故选:B.
二.多选题(共4小题)
6.双曲C1:=1与C2:=λ(λ>0且λ≠1)的( )
A.顶点相同 B.焦点相同 C.离心率相同 D.渐近线相同
【解答】解:由C2:=λ得,
C2:,e===;渐近线y=±=±x=±x;顶点(±2,0),(0,±);焦点(±,0).
双曲线C1:=1,e===;渐近线y=±=±x;顶点(±2,0),(0,±1);焦点(±,0).
∴离心率相同,渐近线相同.
故选:CD.
7.已知双曲线,下列对双曲线C的判断正确的是( )
A.实轴长是虚轴长的2倍 B.焦距为4
C.离心率为 D.渐近线方程为
【解答】解:双曲线的焦点在x轴上,且b=1,a=,c=2,渐近线方程为y=±x.
对于A,实轴长是2,虚轴长是2,故错;
对于B,焦距为2c=4,故正确;
对于C,离心率e==,故错;
对于D,渐近线方程为y=,即,故正确.
故选:BD.
8.已知中心在原点,焦点在坐标轴上的双曲线C与椭圆有相同的焦距,且一条渐近线方程为x﹣2y=0,则双曲线C的方程可能为( )
A. B. C. D.
【解答】解:双曲线C与椭圆有相同的焦距,可得c=,
一条渐近线的方程为x﹣2y=0,
可得a=2b,又c2=a2+b2,解得a=2,b=1,
所以双曲线方程为:﹣y2=1或y2﹣=1.
故选:AD.
9.若双曲线C的一个焦点为F(5,0),P是双曲线上一点,且渐近线方程为,则下列结论正确的是( )
A.C的方程为
B.C的离心率为
C.焦点到渐近线的距离为3
D.|PF|的最小值为2
【解答】解:由双曲线是焦点坐标,设双曲线的方程为﹣=1,
所以渐近线的方程为y=±x,即bx±ay=0,
由题意=,即b=a,
再由c2=a2+b2=a2+(a)2=a2=25,
可得a2=9,b2=16,
所以双曲线的方程为﹣=1,所以A正确,
离心率e==,所以B不正确;
焦点F到渐近线的距离d==b=4,所以C不正确;
|PF|的最小值为c﹣a=5﹣3=2,所以D正确.
故选:AD.
三.填空题(共5小题)
10.若双曲线的焦点与椭圆的焦点相同,则实数t= 9 .
【解答】解:∵双曲线的焦点与椭圆的焦点相同,
∴7+t=25﹣9,
∴t=9
故答案为:9.
11.已知双曲线C1:﹣=1,与C1共渐近线的双曲线C2过(2,4),则C2的方程是 ﹣=1 .
【解答】解:由题意可设与C1共渐近线的双曲线C2的方程为﹣=λ(λ≠0,λ≠1),
由双曲线C2过(2,4),可得﹣=λ,
即λ=﹣1,
所以C2的方程是﹣=1.
故答案为:﹣=1.
12.已知双曲线﹣=1的焦点为F1,F2,过右焦点F2的直线交双曲线右支于A、B两点,若|AF1|+|BF1|=2|AB|,则|AB|等于 8 .
【解答】解:双曲线﹣=1的a=2,
由双曲线的定义可得|AF1|﹣|AF2|=2a,|BF1|﹣|BF2|=2a,
相加可得|AF1|+|BF1|﹣(|AF2|+|BF2|)=|AF1|+|BF1|﹣|AB|=4a,
又|AF1|+|BF1|=2|AB|,可得2|AB|﹣|AB|=4a=8.
故答案为:8.
13.已知双曲线E:=1(b>0)的渐近线方程为y=±x,则双曲线E的焦距等于 4 .
【解答】解:因为双曲线E:=1(b>0),
所以a=,
渐近线方程为y=±x=±x=±x,
所以b=3,
所以c===2,
所以焦距2c=4,
故答案为:4.
14.双曲线的右焦点到渐近线的距离为 2 .
【解答】解:在双曲线中,a2=1,b2=4,
∴c==,
则双曲线的右焦点坐标为F(,0),一条渐近线方程为y=2x,即2x﹣y=0.
∴双曲线的右焦点到一条渐近线的距离为d==2.
故答案为:2.
四.解答题(共2小题)
15.根据下列条件,求双曲线的标准方程.
(1)与双曲线=1有公共焦点,且经过点(4,3);
(2)焦点为(0,±5),且渐近线方程为y=±2x.
【解答】解:(1)由题意设双曲线的方程为:﹣=1,﹣20<k<5,
将(4,3)代入﹣=1,解得:k=﹣11,
所以双曲线的方程为:﹣=1;
(2)由题意设双曲线的方程为:﹣=1,(a>0,b>0),
由题意可得,解得a2=20,b2=5,
所以双曲线的方程为:﹣=1.
16.设F1、F2是双曲线的左、右焦点,点P在该双曲线上,且PF1⊥PF2,求△PF1F2的面积.
【解答】解:由PF1⊥PF2知,点P在以F1F2为直径的圆x2+y2=3上,,
所以△PF1F2的面积为.
声明:试题解析著作权属所有,未经书面同意,不得复制发布
日期:2021/12/1 19:56:43;用户:高中数学;邮箱:gzsxx@;学号:29081547
1
双曲线及其标准方程
知识点一 双曲线的定义
1.定义:平面内与两个定点F1,F2的距离的差的绝对值等于非零常数(小于|F1F2|)的点的轨迹.
2.定义的集合表示:{M|||MF1|-|MF2||=2a,0<2a<|F1F2|}.
3.焦点:两个定点F1,F2.
4.焦距: 两焦点间 的距离,表示为|F1F2|.
注意: (1)当2a<|F1F2|时,P点的轨迹是双曲线.
(2)当2a=|F1F2|时,P点的轨迹是两条射线.
(3)当2a>|F1F2|时,P点不存在.
例题1:在平面直角坐标系xOy中,已知点F1(﹣5,0),F2(5,0),动点P满足|PF1|﹣|PF2|=8,则点P的轨迹是( )
A.椭圆 B.双曲线
C.双曲线的左支 D.双曲线的右支
变式1:平面内到两定点F1(﹣3,0)、F2(3,0)的距离之差的绝对值等于4的点M的轨迹( )
A.椭圆 B.线段 C.两条射线 D.双曲线
知识点二 双曲线标准方程
焦点位置 焦点在x轴上 焦点在y轴上
图形
标准方程 -=1(a>0,b>0) -=1(a>0,b>0)
焦点 (-c,0),(c,0) (0,-c),(0,c)
a,b,c的关系 c2=a2+b2
例题2:(1)已知双曲线-=1(a>0,b>0)的左、右焦点分别为F1,F2,点P在双曲线的右支上,若|PF1|-|PF2|=b,且双曲线的焦距为2,则该双曲线的方程为__________.
(2) “m<3”是“方程+=1表示双曲线”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
(3)求满足下列条件的双曲线的标准方程:
(Ⅰ)c=5,b=3,焦点在x轴上;
(Ⅱ)a=2,经过点A(2,﹣5),焦点在y轴上.
(Ⅲ)经过两点(3,0),(﹣6,﹣3);
变式2:(1)设动点P到A(-5,0)的距离与它到B(5,0)距离的差等于6,则P点的轨迹方程是( )
A.-=1 B.-=1
C.-=1(x≤-3) D.-=1(x≥3)
(2)命题p:“3<m<4”是命题q:“曲线=1表示双曲线”的( )
A.充要条件 B.必要不充分条件
C.充分不必要条件 D.既不充分也不必要条件
(3)求适合下列条件的双曲线的标准方程:
(Ⅰ)求实轴长为2,焦距为4的双曲线的标准方程;
(Ⅱ),经过点(﹣5,2),焦点在x轴上.
(Ⅲ)求以A(﹣3,0)为一个焦点,实轴长为的双曲线的标准方程.
知识点三 双曲线的性质
标准方程 -=1(a>0,b>0) -=1(a>0,b>0)
图形
性质 范围 x≥a或x≤-a y≤-a或y≥a
对称性 对称轴:坐标轴;对称中心:原点
顶点坐标 A1(-a,0),A2(a,0) A1(0,-a),A2(0,a)
渐近线 y=±x y=±x
离心率 e=,e∈(1,+∞),其中c=
a,b,c间的关系 c2=a2+b2(c>a>0,c>b>0)
注意:实轴和虚轴 等长 的双曲线,它的渐近线方程是 y=±x ,离心率为.
例题3:求双曲线nx2-my2=mn(m>0,n>0)的实半轴长、虚半轴长、焦点坐标、离心率、顶点坐标和渐近线方程.
变式3:求双曲线25y2-144x2=3600的实半轴长和虚半轴长、焦点坐标、离心率、渐近线方程.
重难点
重点一、双曲线方程问题
巧设双曲线方程
(1)与双曲线-=1(a>0,b>0)有共同渐近线的方程可表示为-=λ(λ≠0).
(2)过已知两个点的双曲线方程可设为mx2﹣ny2=1(mn>0).
例题4:求下列双曲线方程
(1)已知双曲线过点(3,﹣2)和点(,1);
(2)已知双曲线C过点(,-1),且与双曲线=1有相同的渐近线.
变式4:求满足下列条件的双曲线方程
(1)已知双曲线经过两点A(,), B(,);
(2)已知双曲线C过点M(2,2),且与x2﹣4y2=4有相同的渐近线.
重点二、双曲线渐近线与离心率问题
例题5:(1)已知曲线C:=1(a>0,b>0)其中一条渐近线与直线l:x+2y=2平行,则此双曲线的离心率是( )
A. B. C. D.
(2)已知双曲线C:=1(a>0,b>0)的左、右焦点分别为F1,F2,以|F1F2|为直径的圆交双曲线的右支于点P,若∠PF1F2=30°,则双曲线C的离心率为( )
A. B. C. D.
变式5:若点M(4,0)到双曲线C:=1(b>0)的一条渐近线的距离为2,则双曲线C的离心率为( )
A.2 B. C. D.
(2)已知双曲线=1(a>0,b>0)的左、右焦点分别为F1,F2,双曲线上有一点A,若|F1F2|=10,|AF1|+|AF2|=14,且AF1⊥AF2,则双曲线的渐近线方程为( )
A.y=±5x B.y=x C.y=x D.y=x
课堂反馈
一.选择题(共5小题)
1.已知M(﹣2,0),N(2,0),|PM|﹣|PN|=4,则动点P的轨迹是( )
A.一条射线 B.双曲线 C.双曲线左支 D.双曲线右支
2.“n>m>0”是“方程=1表示焦点在y轴上的双曲线”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.既不充分也不必要条件
3.双曲线C:=1(m>0)的一条渐近线的方程为2x+y=0,则双曲线C的离心率为( )
A. B.2 C.4 D.
4.椭圆C1:=1与双曲线C2:=1(a>0,b>0)的离心率之积为1,则双曲线的渐近线方程为( )
A.y=±2x B.y=x C.y=±x D.y=x
5.已知双曲线=1(a>0,b>0)的左、右焦点分别为F1,F2,双曲线上有一点A,若|F1F2|=10,|AF1|+|AF2|=14,且AF1⊥AF2,则双曲线的渐近线方程为( )
A.y=±5x B.y=±2x C.y=±x D.y=±2x
二.多选题(共4小题)
6.双曲C1:=1与C2:=λ(λ>0且λ≠1)的( )
A.顶点相同 B.焦点相同 C.离心率相同 D.渐近线相同
7.已知双曲线C:=1,下列对双曲线C的判断正确的是( )
A.实轴长是虚轴长的2倍 B.焦距为4
C.离心率为 D.渐近线方程为x±y=0
8.已知中心在原点,焦点在坐标轴上的双曲线C与椭圆=1有相同的焦距,且一条渐近线方程为
x﹣2y=0,则双曲线C的方程可能为( )
A.=1 B.=1 C.=1 D.=1
9.若双曲线C的一个焦点为F(5,0),P是双曲线上一点,且渐近线方程为y=x,则下列结论正确的是( )
A.C的方程为=1 B.C的离心率为
C.焦点到渐近线的距离为3 D.|PF|的最小值为2
三.填空题(共5小题)
10.若双曲线=1的焦点与椭圆=1的焦点相同,则实数t= .
11.已知双曲线C1:=1,与C1共渐近线的双曲线C2过(2,4),则C2的方程是 .
12.已知双曲线=1的焦点为F1,F2,过右焦点F2的直线交双曲线右支于A、B两点,
若|AF1|+|BF1|=2|AB|,则|AB|等于 .
13.已知双曲线E:=1(b>0)的渐近线方程为y=±x,则双曲线E的焦距等于 .
14.双曲线=1的右焦点到渐近线的距离为 .
四.解答题(共2小题)
15.根据下列条件,求双曲线的标准方程.
(1)与双曲线=1有公共焦点,且经过点(4,3);
(2)焦点为(0,±5),且渐近线方程为y=±2x.
16.设F1、F2是双曲线=1的左、右焦点,点P在该双曲线上,且PF1⊥PF2,求△PF1F2的面积.
声明:试题解析著作权属所有,未经书面同意,不得复制发布
日期:2021/12/1 19:56:43;用户:高中数学;邮箱:gzsxx@;学号:29081547
答案解析
例题1:在平面直角坐标系xOy中,已知点F1(﹣5,0),F2(5,0),动点P满足|PF1|﹣|PF2|=8,则点P的轨迹是( )
A.椭圆 B.双曲线
C.双曲线的左支 D.双曲线的右支
【解答】解:由于两点间的距离|F1F2|=10,动点P满足|PF1|﹣|PF2|=8<10,
所以满足条件|PF1|﹣|PF2|=8的点P的轨迹是双曲线中离F2较近的一支.
故选:D.
变式1:平面内到两定点F1(﹣3,0)、F2(3,0)的距离之差的绝对值等于4的点M的轨迹( )
A.椭圆 B.线段 C.两条射线 D.双曲线
【解答】解:根据双曲线的定义,
|MF1|﹣|MF2|=±4,
且|F1F2|=6>4,
∴点M的轨迹是焦点在x轴上的双曲线,且焦距为6.
故选:D.
例题2:(1)已知双曲线-=1(a>0,b>0)的左、右焦点分别为F1,F2,点P在双曲线的右支上,若|PF1|-|PF2|=b,且双曲线的焦距为2,则该双曲线的方程为__________.
(2) “m<3”是“方程+=1表示双曲线”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
【解答】解:当为双曲线时,(m+2)(m﹣3)<0
∴﹣2<m<3,
∵(﹣2,3) (3,+∞)
故选:B.
(3)求满足下列条件的双曲线的标准方程:
(Ⅰ)c=5,b=3,焦点在x轴上;
(Ⅱ),经过点A(2,﹣5),焦点在y轴上.
(Ⅲ)经过两点(3,0),(﹣6,﹣3);
【解答】解:(Ⅰ)∵双曲线的焦点在x轴上,c=5,b=3,
∴a2=c2﹣b2=16,
∴双曲线方程为:;
(Ⅱ)∵双曲线的焦点在y轴上,
∴可设双曲线的标准方程为,
∵由题设知,,且点A(2,﹣5)在双曲线上,
∴
∴解得a2=20,b2=16,
∴所求双曲线的标准方程为.
(Ⅲ)根据题意,若双曲线经过点(3,0),
则双曲线的焦点在x轴上,且a=3,设其标准方程为﹣=1;
又由双曲线经过点(﹣6,﹣3),则有4﹣=1,则b2=3,
则双曲线的标准方程为﹣=1;
变式2:(1)设动点P到A(-5,0)的距离与它到B(5,0)距离的差等于6,则P点的轨迹方程是( )
A.-=1 B.-=1
C.-=1(x≤-3) D.-=1(x≥3)
【解答】由题意知,轨迹应为以A(-5,0),B(5,0)为焦点的双曲线的右支.
由c=5,a=3,知b2=16,
∴P点的轨迹方程为-=1(x≥3).
答案 D
(2)命题p:“3<m<4”是命题q:“曲线表示双曲线”的( )
A.充要条件 B.必要不充分条件
C.充分不必要条件 D.既不充分也不必要条件
【解答】解:3<m<5 曲线表示双曲线,
因为曲线表示双曲线,
所以(m﹣3)(5﹣m)>0,解得3<m<5,
∴命题p:“3<m<4”是命题q:“曲线表示双曲线”的充分不必要条件.
故选:C.
(3)求适合下列条件的双曲线的标准方程:
(Ⅰ)(Ⅰ)求实轴长为2,焦距为4的双曲线的标准方程;
(Ⅱ),经过点(﹣5,2),焦点在x轴上.
(Ⅲ)求以A(﹣3,0)为一个焦点,实轴长为的双曲线的标准方程.
【解答】解:(Ⅰ)根据题意,要求椭圆的实轴长为2,焦距为4,即2a=2,2c=4,
则a=1,c=2,则b==;
若要求椭圆的焦点在x轴上,则其标准方程为x2-=1,
若要求椭圆的焦点在y轴上,则其标准方程为y2-=1,
故要求椭圆的标准方程为x2-=1或y2-=1;
(Ⅱ)∵焦点在x轴上,,
∴设所求双曲线方程为:(其中0<λ<6)
∵双曲线经过点(﹣5,2),∴
∴λ=5或λ=30(舍去)
∴所求双曲线方程是
(Ⅲ)要求双曲线以A(﹣3,0)为一个焦点,实轴长为,
则其焦点在x轴上,且c=3,2a=2,即a=,
则b==2,
则要求双曲线的标准方程为.
例题3:求双曲线nx2-my2=mn(m>0,n>0)的实半轴长、虚半轴长、焦点坐标、离心率、顶点坐标和渐近线方程.
【解答】把方程nx2-my2=mn(m>0,n>0)化为标准方程为-=1(m>0,n>0),
由此可知,实半轴长a=,
虚半轴长b=,c=,
焦点坐标为(,0),(-,0),
离心率e===,
顶点坐标为(-,0),(,0),
所以渐近线方程为y=± x,即y=±x.
变式3:求双曲线25y2-144x2=3600的实半轴长和虚半轴长、焦点坐标、离心率、渐近线方程.
解 把方程25y2-144x2=3600化为标准方程为.
由此可知,实半轴长a=12,虚半轴长b=5;
c===13,焦点坐标是(0,-13),(0,13);
离心率e==;渐近线方程为y=x.
例题4:求下列双曲线方程
(1)已知双曲线过点(3,﹣2)和点;
已知双曲线C过点,且与双曲线=1有相同的渐近线.
【解答】解:(1)若双曲线焦点在x轴上,设双曲线C的标准方程为:mx2﹣ny2=1(mn>0),
则,解得m,n,
∴双曲线C的标准方程是:.
(2)设与双曲线=1有相同的渐近线的双曲线C的方程为:﹣=λ,
由双曲线C过点(2,﹣1)可得:﹣=λ,解得λ=,
所以双曲线C的标准方程:﹣=1;
故答案为:﹣=1.
变式4:求满足下列条件的双曲线方程
(1)已知双曲线经过两点,;
(2)已知双曲线C过点M(2,2),且与x2﹣4y2=4有相同的渐近线.
【解答】(1)解:设双曲线的方程为nx2﹣my2=1,mn>0,
把两点,代入,得:,
解得n=1,m=,
∴所求的双曲线方程为x2﹣=1,c=,
双曲线的焦距为:.
(2)解:设与x2﹣4y2=4有相同的渐近线的双曲线方程为与x2﹣4y2=4λ(λ≠0),
代入点M(2,2),得22﹣4×22=4λ,即λ=﹣3.
∴双曲线C的方程为.
故答案为:.
例题5:(1)已知曲线其中一条渐近线与直线l:x+2y=2平行,则此双曲线的离心率是( )
A. B. C. D.
【解答】解:根据题意,双曲线C的方程为(a>0,b>0),
则其渐近线方程为y=±x,
又由其一条渐近线与直线l:x+2y=2平行,有=,即b=a,
则c==a=a,
则其离心率e==,
故选:B.
(2)已知双曲线C:=1(a>0,b>0)的左、右焦点分别为F1,F2,以|F1F2|为直径的圆交双曲线的右支于点P,若∠PF1F2=30°,则双曲线C的离心率为( )
A. B. C. D.
【解答】解:设|F1F2|=2c,
由于P是以F1F2为直径的圆与该双曲线的一个交点
则△F1F2P是直角三角形,∠F1PF2=90°,
由∠PF1F2=30°,
∴|PF1|=c,|PF2|=c,
∴|PF1|﹣|PF2|=c﹣c=2a,
∴e===.
故选:D.
变式5:若点M(4,0)到双曲线C:=1(b>0)的一条渐近线的距离为2,则双曲线C的离心率为( )
A.2 B. C. D.
【解答】解:由双曲线的对称性,M到任意一条渐近线的距离相等,
由双曲线的方程可得渐近线的方程:y=±x,
即bx±3y=0,
所以M到渐近线的距离d=,
所以2=,b>0,
可得:b2=3,
所以双曲线的离心率e====,
故选:D.
(2)已知双曲线的左、右焦点分别为F1,F2,双曲线上有一点A,若|F1F2|=10,|AF1|+|AF2|=14,且AF1⊥AF2,则双曲线的渐近线方程为( )
A.y=±5x B. C. D.
【解答】解:设|AF1|=m,|AF2|=n,,由|AF1|+|AF2|=14,得m+n=14,
又AF1⊥AF2,所以m2+n2=102,
解方程组,得m=8,n=6或m=6,n=8;
所以||AF1|﹣|AF2||=2=2a,所以a=1,
又|F1F2|=10,所以c=5,
所以b==2,
双曲线的渐近线方程为y=±2x,
故选:B.
课堂反馈
一.选择题(共5小题)
1.已知M(﹣2,0),N(2,0),|PM|﹣|PN|=4,则动点P的轨迹是( )
A.一条射线 B.双曲线 C.双曲线左支 D.双曲线右支
【解答】解:如果是双曲线,那么|PM|﹣|PN|=4=2a
a=2
而两个定点M(﹣2,0),N(2,0)为双曲线的焦点
c=2
而在双曲线中c>a
所以把后三个关于双曲线的答案全部排除,
故选:A.
2.“n>m>0”是“方程表示焦点在y轴上的双曲线”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.既不充分也不必要条件
【解答】解:若n>m>0,则方程表示焦点在y轴上的双曲线,
若方程表示焦点在y轴上的双曲线,则n>0且m>0,
所以“n>m>0”是“方程表示焦点在y轴上的双曲线”充分不必要条件.
故选:A.
3.双曲线C:=1(m>0)的一条渐近线的方程为2x+y=0,则双曲线C的离心率为( )
A. B.2 C.4 D.
【解答】解:根据题意,双曲线C:=1(m>0)的一条渐近线的方程为2x+y=0,
则有,即m=8,
则双曲线的方程为双曲线:=1,
其中a=,b=2,则c=,
则双曲线的离心率e==.
故选:D.
4.椭圆C1:=1与双曲线C2:=1(a>0,b>0)的离心率之积为1,则双曲线的渐近线方程为( )
A.y=±2x B. C. D.
【解答】解:设椭圆的离心率为e1,则e1=,
双曲线的离心率为e2,
由题意可得e1e2== =1,
可得=,
由双曲线C2的渐近线方程为y=±x,即y=±x,
故选:D.
5.已知双曲线的左、右焦点分别为F1,F2,双曲线上有一点A,若|F1F2|=10,|AF1|+|AF2|=14,且AF1⊥AF2,则双曲线的渐近线方程为( )
A.y=±5x B. C. D.
【解答】解:设|AF1|=m,|AF2|=n,,由|AF1|+|AF2|=14,得m+n=14,
又AF1⊥AF2,所以m2+n2=102,
解方程组,得m=8,n=6或m=6,n=8;
所以||AF1|﹣|AF2||=2=2a,所以a=1,
又|F1F2|=10,所以c=5,
所以b==2,
双曲线的渐近线方程为y=±2x,
故选:B.
二.多选题(共4小题)
6.双曲C1:=1与C2:=λ(λ>0且λ≠1)的( )
A.顶点相同 B.焦点相同 C.离心率相同 D.渐近线相同
【解答】解:由C2:=λ得,
C2:,e===;渐近线y=±=±x=±x;顶点(±2,0),(0,±);焦点(±,0).
双曲线C1:=1,e===;渐近线y=±=±x;顶点(±2,0),(0,±1);焦点(±,0).
∴离心率相同,渐近线相同.
故选:CD.
7.已知双曲线,下列对双曲线C的判断正确的是( )
A.实轴长是虚轴长的2倍 B.焦距为4
C.离心率为 D.渐近线方程为
【解答】解:双曲线的焦点在x轴上,且b=1,a=,c=2,渐近线方程为y=±x.
对于A,实轴长是2,虚轴长是2,故错;
对于B,焦距为2c=4,故正确;
对于C,离心率e==,故错;
对于D,渐近线方程为y=,即,故正确.
故选:BD.
8.已知中心在原点,焦点在坐标轴上的双曲线C与椭圆有相同的焦距,且一条渐近线方程为x﹣2y=0,则双曲线C的方程可能为( )
A. B. C. D.
【解答】解:双曲线C与椭圆有相同的焦距,可得c=,
一条渐近线的方程为x﹣2y=0,
可得a=2b,又c2=a2+b2,解得a=2,b=1,
所以双曲线方程为:﹣y2=1或y2﹣=1.
故选:AD.
9.若双曲线C的一个焦点为F(5,0),P是双曲线上一点,且渐近线方程为,则下列结论正确的是( )
A.C的方程为
B.C的离心率为
C.焦点到渐近线的距离为3
D.|PF|的最小值为2
【解答】解:由双曲线是焦点坐标,设双曲线的方程为﹣=1,
所以渐近线的方程为y=±x,即bx±ay=0,
由题意=,即b=a,
再由c2=a2+b2=a2+(a)2=a2=25,
可得a2=9,b2=16,
所以双曲线的方程为﹣=1,所以A正确,
离心率e==,所以B不正确;
焦点F到渐近线的距离d==b=4,所以C不正确;
|PF|的最小值为c﹣a=5﹣3=2,所以D正确.
故选:AD.
三.填空题(共5小题)
10.若双曲线的焦点与椭圆的焦点相同,则实数t= 9 .
【解答】解:∵双曲线的焦点与椭圆的焦点相同,
∴7+t=25﹣9,
∴t=9
故答案为:9.
11.已知双曲线C1:﹣=1,与C1共渐近线的双曲线C2过(2,4),则C2的方程是 ﹣=1 .
【解答】解:由题意可设与C1共渐近线的双曲线C2的方程为﹣=λ(λ≠0,λ≠1),
由双曲线C2过(2,4),可得﹣=λ,
即λ=﹣1,
所以C2的方程是﹣=1.
故答案为:﹣=1.
12.已知双曲线﹣=1的焦点为F1,F2,过右焦点F2的直线交双曲线右支于A、B两点,若|AF1|+|BF1|=2|AB|,则|AB|等于 8 .
【解答】解:双曲线﹣=1的a=2,
由双曲线的定义可得|AF1|﹣|AF2|=2a,|BF1|﹣|BF2|=2a,
相加可得|AF1|+|BF1|﹣(|AF2|+|BF2|)=|AF1|+|BF1|﹣|AB|=4a,
又|AF1|+|BF1|=2|AB|,可得2|AB|﹣|AB|=4a=8.
故答案为:8.
13.已知双曲线E:=1(b>0)的渐近线方程为y=±x,则双曲线E的焦距等于 4 .
【解答】解:因为双曲线E:=1(b>0),
所以a=,
渐近线方程为y=±x=±x=±x,
所以b=3,
所以c===2,
所以焦距2c=4,
故答案为:4.
14.双曲线的右焦点到渐近线的距离为 2 .
【解答】解:在双曲线中,a2=1,b2=4,
∴c==,
则双曲线的右焦点坐标为F(,0),一条渐近线方程为y=2x,即2x﹣y=0.
∴双曲线的右焦点到一条渐近线的距离为d==2.
故答案为:2.
四.解答题(共2小题)
15.根据下列条件,求双曲线的标准方程.
(1)与双曲线=1有公共焦点,且经过点(4,3);
(2)焦点为(0,±5),且渐近线方程为y=±2x.
【解答】解:(1)由题意设双曲线的方程为:﹣=1,﹣20<k<5,
将(4,3)代入﹣=1,解得:k=﹣11,
所以双曲线的方程为:﹣=1;
(2)由题意设双曲线的方程为:﹣=1,(a>0,b>0),
由题意可得,解得a2=20,b2=5,
所以双曲线的方程为:﹣=1.
16.设F1、F2是双曲线的左、右焦点,点P在该双曲线上,且PF1⊥PF2,求△PF1F2的面积.
【解答】解:由PF1⊥PF2知,点P在以F1F2为直径的圆x2+y2=3上,,
所以△PF1F2的面积为.
声明:试题解析著作权属所有,未经书面同意,不得复制发布
日期:2021/12/1 19:56:43;用户:高中数学;邮箱:gzsxx@;学号:29081547
1
