河南省郑州106中学2022届高三上学期五调考试数学(理)试卷(Word版,含答案)
文档属性
| 名称 | 河南省郑州106中学2022届高三上学期五调考试数学(理)试卷(Word版,含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 981.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-03 13:47:21 | ||
图片预览

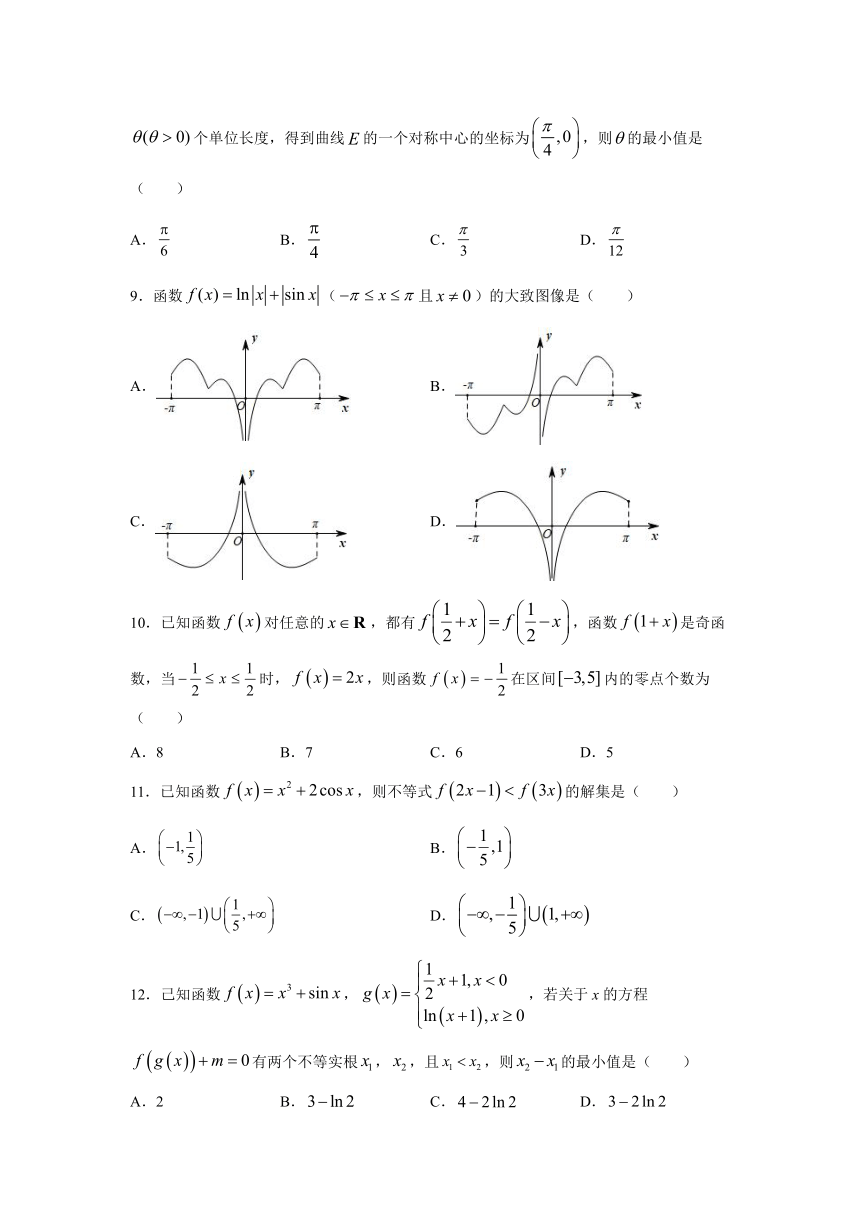



文档简介
郑州106中学2022届高三五调考试
理科数学试卷
(满分150分,时间120分钟)
一、单选题(每小题5分,共60分)
1.已知复数满足,则复数在复平面内表示的点所在的象限为( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.变量满足,若存在使得,则k的最大值是( )
A.5 B.6 C.8 D.9
3.设为等比数列的前项和且,则( )
A. B. C. D.
4.已知,“对恒成立”的一个充分不必要条件是( )
A. B. C. D.
5.函数的单调递减区间是( )
A. B. C. D.
6.在中,角A,B,C所对的边分别为a,b,c,若角A,B,C依次成等差数列,边a,b,c依次成等比数列,且,则( )
A. B. C. D.
7.若实数,满足,则的最小值为( )
A. B. C. D.
8.已知曲线的一条对称轴方程为,曲线向左平移个单位长度,得到曲线的一个对称中心的坐标为,则的最小值是( )
A. B. C. D.
9.函数(且)的大致图像是( )
A. B.
C. D.
10.已知函数对任意的,都有,函数是奇函数,当时,,则函数在区间内的零点个数为( )
A.8 B.7 C.6 D.5
11.已知函数,则不等式的解集是( )
A. B.
C. D.
12.己知函数,,若关于x的方程有两个不等实根,,且,则的最小值是( )
A.2 B. C. D.
二、填空题(每小题5分,共20分)
13.已知数列的首项,,那么___________.
14.已知向量,,则向量在向量上的投影为___________.
15.记等差数列的前项和,利用倒序求和的方法得:;类似的,记等比数列的前项的积为,且,试类比等差数列求和的方法,可将表示成首项,末项与项数的一个关系式,即公式_______________.
16.设定义域为的函数满足,则不等式的解集为__________.
三、解答题(每大题12分,22题10分)
17.已知命题:“,使得”为假命题.
(1)求实数的取值集合;(2)设不等式的解集为集合,若是的充分不必要条件,求实数的取值范围.
18.已知.
(1)求的值域.
(2)若对任意和都成立,求的取值范围.
19.设的内角所对的边分别为,已知.
(Ⅰ)求角的大小;(Ⅱ)若,边上的中线,求的面积.
20.已知数列中,.
(1)求证:是等比数列,并求的通项公式;
(2)数列满足,数列的前项和为,若不等式对一切恒成立,求的取值范围.
21.已知函数.
(1)当时,证明不等式;
(2)若不等式恒成立,求实数的取值范围.
选做题:(以下两道任选一道,共10分)
22.在平面直角坐标系中,曲线的参数方程为为参数,.以原点为极点,轴的非负半轴为极轴建立极坐标系,曲线的极坐标方程为.
(1)写出曲线的普通方程和曲线的直角坐标方程:
(2)已知,点是曲线上一点,点到曲线的最大距离为,求的值.
23.函数.
(1)当时,求不等式的解集;
(2)若不等式的解集为空集,求的取值范围.
答案
ADDAB DDCDA CD
13.
14. 13.
15.
16.
17.(1).(2)或
【解析】
【分析】
(1)写出命题的否定得恒成立,列出满足条件的不等式即可求解;
(2)根据题意知集合是集合的真子集,分类讨论,分别列出满足的不等式求解即可.
【详解】
(1)命题“,使方程”是真命题.
只需,
解得,
于是可得:
(2)若是的必要不充分条件,则集合是集合的真子集.
当时,,不合题意,
当时,,
由AB可得:,
解得;
当时,,
由AB可得:,
解得;
综上或.
18.(1); (2).
【解析】
【分析】
(1)利用换元法,将函数转化为关于t的二次函数,根据t的取值范围求得函数的值域.
(2)根据恒成立条件,得到关于m的二次函数表达式;利用变换主元法看成关于a的函数表达式,进而求得m的取值范围.
【详解】
(1)令
原函数变为:
的值域为.
(2)
即
恒成立
令,
图象为线段,
则
解得.
19.【答案】(Ⅰ)(Ⅱ)
【解析】
【分析】
(Ⅰ)由正弦定理化简得到答案.
(Ⅱ),平方,代入公式利用余弦定理得到答案.
【详解】
(Ⅰ)因为,
由正弦定理得,
即,所以,
因为,所以,
又因为,所以.
(Ⅱ)由M是中点,得,
即,
所以,①
又根据余弦定理,有,②
联立①②,得.
所以的面积.
20.(1)证明祥见解析,;(2).
【解析】
【试题分析】(1)依据题设条件将递推关系式进行合理变形,再运用等比数列的定义分析推证,进而求出数列的通项公式;(2)借助题设条件,运用错位相减法求出数列的前项和然后再运用分类整合思想,分类探求满足不等式的实数的取值范围:
(1)证明:由,
得,
所以数列是以3为公比,以为首项的等比数列,
从而;
(2)
, 两式相减得
若为偶数,则
若为奇数,则
21.(1)证明见详解;(2)
【解析】
【分析】
(1)将代入,求出,记,利用导数判断函数的单调性,求出函数的最大值,即可.
(2)将不等式转化为在恒成立,构造函数,根据单调性可得,只需恒成立,记,利用导数求出即可.
【详解】
(1)当时,,函数的定义域为
所以,
记,
所以,
当时,,单调递减,
又因为,,
所以存在,使得,
所以当时,,即,
当时,,即,
所以,
又因为,
所以,
即,所以,即证.
(2)不等式恒成立等价于在恒成立,
即在恒成立,
也就是在恒成立,
构造函数,,
所以在单调递增,
所以,
即,
记,
所以,
当时,,单调递减,
当时,,单调递增,
所以,
所以,故实数的取值范围.
22.(1);;(2).
【解析】
【分析】
(1)直接利用转换关系,把参数方程极坐标方程和直角坐标方程之间进行转换.
(2)利用点到直线的距离公式的应用和三角函数关系式的恒等变换及正弦型函数的性质的应用求出结果.
【详解】
(1)曲线的参数方程为为参数,.
转换为直角坐标法方程为.
曲线的极坐标方程为,
根据转换为直角坐标方程为.
(2)设点是曲线上一点,则点到曲线的距离,
由于,所以,
则:.
由点到曲线的最大距离为,所以的最大值为4,
由于,所以,则,即,
故.
23.(1)(2)
【解析】
【分析】
(1)由得,分,,三种情况讨论,即可得出结果;
(2)先由的解集为空集,得恒成立,再由绝对值不等式的性质求出的最大值,即可得出结果.
【详解】
解:(1)当时,不等式,即,
当时,原不等式可化为,即,显然不成立,此时原不等式无解;
当时,原不等式可化为,解得;
当时,原不等式可化为,即,显然成立,即满足题意;
综上,原不等式的解集为;
(2)由的解集为空集,得的解集为空集,
所以恒成立,
因为,所以,
所以当且仅当,即时,,
所以,解得,
即的取值范围是.
理科数学试卷
(满分150分,时间120分钟)
一、单选题(每小题5分,共60分)
1.已知复数满足,则复数在复平面内表示的点所在的象限为( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.变量满足,若存在使得,则k的最大值是( )
A.5 B.6 C.8 D.9
3.设为等比数列的前项和且,则( )
A. B. C. D.
4.已知,“对恒成立”的一个充分不必要条件是( )
A. B. C. D.
5.函数的单调递减区间是( )
A. B. C. D.
6.在中,角A,B,C所对的边分别为a,b,c,若角A,B,C依次成等差数列,边a,b,c依次成等比数列,且,则( )
A. B. C. D.
7.若实数,满足,则的最小值为( )
A. B. C. D.
8.已知曲线的一条对称轴方程为,曲线向左平移个单位长度,得到曲线的一个对称中心的坐标为,则的最小值是( )
A. B. C. D.
9.函数(且)的大致图像是( )
A. B.
C. D.
10.已知函数对任意的,都有,函数是奇函数,当时,,则函数在区间内的零点个数为( )
A.8 B.7 C.6 D.5
11.已知函数,则不等式的解集是( )
A. B.
C. D.
12.己知函数,,若关于x的方程有两个不等实根,,且,则的最小值是( )
A.2 B. C. D.
二、填空题(每小题5分,共20分)
13.已知数列的首项,,那么___________.
14.已知向量,,则向量在向量上的投影为___________.
15.记等差数列的前项和,利用倒序求和的方法得:;类似的,记等比数列的前项的积为,且,试类比等差数列求和的方法,可将表示成首项,末项与项数的一个关系式,即公式_______________.
16.设定义域为的函数满足,则不等式的解集为__________.
三、解答题(每大题12分,22题10分)
17.已知命题:“,使得”为假命题.
(1)求实数的取值集合;(2)设不等式的解集为集合,若是的充分不必要条件,求实数的取值范围.
18.已知.
(1)求的值域.
(2)若对任意和都成立,求的取值范围.
19.设的内角所对的边分别为,已知.
(Ⅰ)求角的大小;(Ⅱ)若,边上的中线,求的面积.
20.已知数列中,.
(1)求证:是等比数列,并求的通项公式;
(2)数列满足,数列的前项和为,若不等式对一切恒成立,求的取值范围.
21.已知函数.
(1)当时,证明不等式;
(2)若不等式恒成立,求实数的取值范围.
选做题:(以下两道任选一道,共10分)
22.在平面直角坐标系中,曲线的参数方程为为参数,.以原点为极点,轴的非负半轴为极轴建立极坐标系,曲线的极坐标方程为.
(1)写出曲线的普通方程和曲线的直角坐标方程:
(2)已知,点是曲线上一点,点到曲线的最大距离为,求的值.
23.函数.
(1)当时,求不等式的解集;
(2)若不等式的解集为空集,求的取值范围.
答案
ADDAB DDCDA CD
13.
14. 13.
15.
16.
17.(1).(2)或
【解析】
【分析】
(1)写出命题的否定得恒成立,列出满足条件的不等式即可求解;
(2)根据题意知集合是集合的真子集,分类讨论,分别列出满足的不等式求解即可.
【详解】
(1)命题“,使方程”是真命题.
只需,
解得,
于是可得:
(2)若是的必要不充分条件,则集合是集合的真子集.
当时,,不合题意,
当时,,
由AB可得:,
解得;
当时,,
由AB可得:,
解得;
综上或.
18.(1); (2).
【解析】
【分析】
(1)利用换元法,将函数转化为关于t的二次函数,根据t的取值范围求得函数的值域.
(2)根据恒成立条件,得到关于m的二次函数表达式;利用变换主元法看成关于a的函数表达式,进而求得m的取值范围.
【详解】
(1)令
原函数变为:
的值域为.
(2)
即
恒成立
令,
图象为线段,
则
解得.
19.【答案】(Ⅰ)(Ⅱ)
【解析】
【分析】
(Ⅰ)由正弦定理化简得到答案.
(Ⅱ),平方,代入公式利用余弦定理得到答案.
【详解】
(Ⅰ)因为,
由正弦定理得,
即,所以,
因为,所以,
又因为,所以.
(Ⅱ)由M是中点,得,
即,
所以,①
又根据余弦定理,有,②
联立①②,得.
所以的面积.
20.(1)证明祥见解析,;(2).
【解析】
【试题分析】(1)依据题设条件将递推关系式进行合理变形,再运用等比数列的定义分析推证,进而求出数列的通项公式;(2)借助题设条件,运用错位相减法求出数列的前项和然后再运用分类整合思想,分类探求满足不等式的实数的取值范围:
(1)证明:由,
得,
所以数列是以3为公比,以为首项的等比数列,
从而;
(2)
, 两式相减得
若为偶数,则
若为奇数,则
21.(1)证明见详解;(2)
【解析】
【分析】
(1)将代入,求出,记,利用导数判断函数的单调性,求出函数的最大值,即可.
(2)将不等式转化为在恒成立,构造函数,根据单调性可得,只需恒成立,记,利用导数求出即可.
【详解】
(1)当时,,函数的定义域为
所以,
记,
所以,
当时,,单调递减,
又因为,,
所以存在,使得,
所以当时,,即,
当时,,即,
所以,
又因为,
所以,
即,所以,即证.
(2)不等式恒成立等价于在恒成立,
即在恒成立,
也就是在恒成立,
构造函数,,
所以在单调递增,
所以,
即,
记,
所以,
当时,,单调递减,
当时,,单调递增,
所以,
所以,故实数的取值范围.
22.(1);;(2).
【解析】
【分析】
(1)直接利用转换关系,把参数方程极坐标方程和直角坐标方程之间进行转换.
(2)利用点到直线的距离公式的应用和三角函数关系式的恒等变换及正弦型函数的性质的应用求出结果.
【详解】
(1)曲线的参数方程为为参数,.
转换为直角坐标法方程为.
曲线的极坐标方程为,
根据转换为直角坐标方程为.
(2)设点是曲线上一点,则点到曲线的距离,
由于,所以,
则:.
由点到曲线的最大距离为,所以的最大值为4,
由于,所以,则,即,
故.
23.(1)(2)
【解析】
【分析】
(1)由得,分,,三种情况讨论,即可得出结果;
(2)先由的解集为空集,得恒成立,再由绝对值不等式的性质求出的最大值,即可得出结果.
【详解】
解:(1)当时,不等式,即,
当时,原不等式可化为,即,显然不成立,此时原不等式无解;
当时,原不等式可化为,解得;
当时,原不等式可化为,即,显然成立,即满足题意;
综上,原不等式的解集为;
(2)由的解集为空集,得的解集为空集,
所以恒成立,
因为,所以,
所以当且仅当,即时,,
所以,解得,
即的取值范围是.
同课章节目录
