1.2全等三角形 课件(共13张PPT)
文档属性
| 名称 | 1.2全等三角形 课件(共13张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1018.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-04 12:45:32 | ||
图片预览




文档简介
(共13张PPT)
苏科版 八年级上册
1.2 全等三角形
1.2 全等三角形
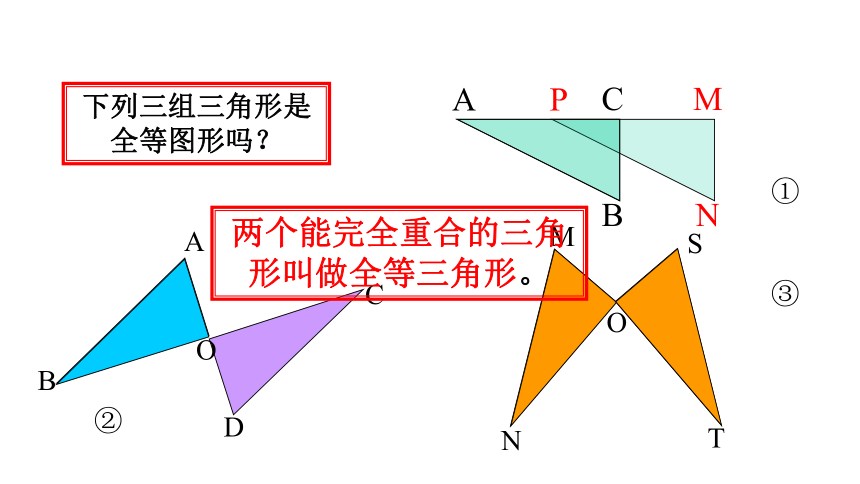
两个能完全重合的图形叫做全等图形
全等图形的形状和大小相同。
②
③
下列三组三角形是全等图形吗?
1.2 全等三角形
D
C
O
A
B
①
N
M
S
O
T
两个能完全重合的三角形叫做全等三角形。
B
A
C
N
P
M
②
③
1.2 全等三角形
D
C
O
A
B
①
N
M
S
O
T
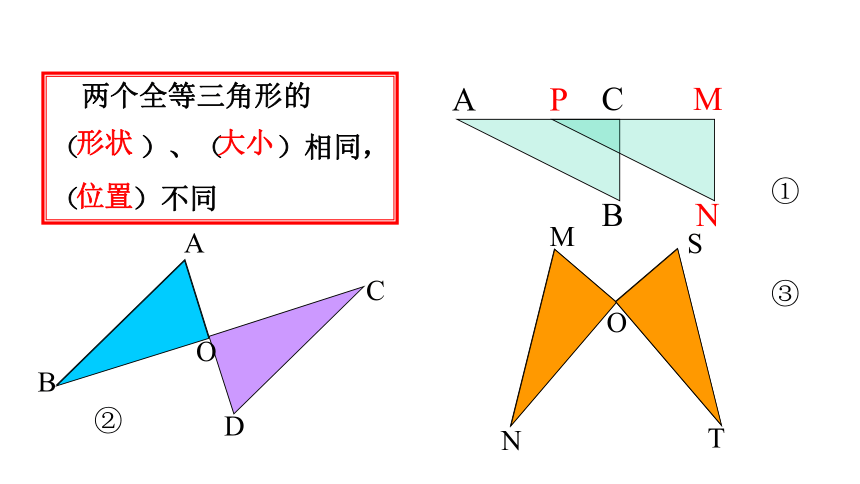
两个全等三角形的
( )、( )相同,
( )不同
大小
形状
位置
B
A
C
N
P
M
②
③
1.2 全等三角形
D
C
O
A
B
①
N
M
S
O
T
两个全等三角形重合时,
互相重合的顶点叫 ,
互相重合的边叫做 ,
互相重合的角叫做 .
对应顶点
对应边
对应角
请指出它们的对应顶点、对应边和对应角。
B
A
C
N
P
M
②
③
1.2 全等三角形
D
C
O
A
B
①
N
M
S
O
T
记作 △ABC ≌ △PNM ,
读作 △ABC 全等于 △PNM.
B
A
C
N
P
M
△ABO ≌ △ ,
DCO
△MNO ≌ △ ,
STO
注意:对应顶点的字母要写在对应的位置上.
请利用两个全等三角形纸板,组合成不同图形。
1、你能拼出几种不同图形?
2、你能改变一个三角形的位置,使它于另一个三角形重合吗?
1.2 全等三角形
3、两个全等三角形位置变化了,对应边、对应角大小有变化吗?
例1 如图,已知:△ABD≌ △EBC,
(1)怎样改变△ABD的位置,使它与△EBC重合?
(2)如果AB=3cm,BC=5cm, 求DE的长.
解:∵ △ABD≌ △EBC (已知)
∴ BE=AB=3cm,BD=BC=5cm
(全等三角形的对应边相等)
∴ DE=BD-BE=5-3=2cm
1.2 全等三角形
解决此类问题的关键是明确全等三角形的对应元素.
1.2 全等三角形
例2 如图,已知△BCE≌△CBD,
(1)怎样改变△BCE的位置,使它与△CBD重合?
(2)求证:∠EBO=∠DCO.
证明:∵ △BCE≌△CBD (已知)
∴ ∠ECB=∠DBC,∠EBC=∠DCB.
(全等三角形对应角相等)
∴ ∠EBC-∠DBC=∠DCB-∠ECB.
(等式的基本性质)
∴ ∠EBO=∠DCO.
练习:如图,△ABD≌△ACE,
(1)若∠ADB=108°,∠B=25°,你能说出△ACE中各角的大小吗?
A
B
C
D
E
解(1)∵△ABD≌△ACE ,
∴ ∠AEC=∠ADB=108°,
∠C =∠B=25° ,
∠A=180°- ∠AEC- ∠C
=180°-108°-25°
=47°
(2)∵ △ABD≌△ACE ,
∴ CE=BD=6cm ,
AE=AD=4cm,
AC=AB=8cm.
(2)若BD=6㎝,AD=4㎝,AB=8cm,你能说出△ACE中各边的长度吗?
1.2 全等三角形
全等三角形
定 义
符号表示
性质
应用
两个能完全重合的三角形叫做全等三角形
对应顶点的字母要写在对应的位置上
全等三角形的对应边相等,对应角相等
对应边、对应角的识别
https://www.21cnjy.com/help/help_extract.php
苏科版 八年级上册
1.2 全等三角形
1.2 全等三角形
两个能完全重合的图形叫做全等图形
全等图形的形状和大小相同。
②
③
下列三组三角形是全等图形吗?
1.2 全等三角形
D
C
O
A
B
①
N
M
S
O
T
两个能完全重合的三角形叫做全等三角形。
B
A
C
N
P
M
②
③
1.2 全等三角形
D
C
O
A
B
①
N
M
S
O
T
两个全等三角形的
( )、( )相同,
( )不同
大小
形状
位置
B
A
C
N
P
M
②
③
1.2 全等三角形
D
C
O
A
B
①
N
M
S
O
T
两个全等三角形重合时,
互相重合的顶点叫 ,
互相重合的边叫做 ,
互相重合的角叫做 .
对应顶点
对应边
对应角
请指出它们的对应顶点、对应边和对应角。
B
A
C
N
P
M
②
③
1.2 全等三角形
D
C
O
A
B
①
N
M
S
O
T
记作 △ABC ≌ △PNM ,
读作 △ABC 全等于 △PNM.
B
A
C
N
P
M
△ABO ≌ △ ,
DCO
△MNO ≌ △ ,
STO
注意:对应顶点的字母要写在对应的位置上.
请利用两个全等三角形纸板,组合成不同图形。
1、你能拼出几种不同图形?
2、你能改变一个三角形的位置,使它于另一个三角形重合吗?
1.2 全等三角形
3、两个全等三角形位置变化了,对应边、对应角大小有变化吗?
例1 如图,已知:△ABD≌ △EBC,
(1)怎样改变△ABD的位置,使它与△EBC重合?
(2)如果AB=3cm,BC=5cm, 求DE的长.
解:∵ △ABD≌ △EBC (已知)
∴ BE=AB=3cm,BD=BC=5cm
(全等三角形的对应边相等)
∴ DE=BD-BE=5-3=2cm
1.2 全等三角形
解决此类问题的关键是明确全等三角形的对应元素.
1.2 全等三角形
例2 如图,已知△BCE≌△CBD,
(1)怎样改变△BCE的位置,使它与△CBD重合?
(2)求证:∠EBO=∠DCO.
证明:∵ △BCE≌△CBD (已知)
∴ ∠ECB=∠DBC,∠EBC=∠DCB.
(全等三角形对应角相等)
∴ ∠EBC-∠DBC=∠DCB-∠ECB.
(等式的基本性质)
∴ ∠EBO=∠DCO.
练习:如图,△ABD≌△ACE,
(1)若∠ADB=108°,∠B=25°,你能说出△ACE中各角的大小吗?
A
B
C
D
E
解(1)∵△ABD≌△ACE ,
∴ ∠AEC=∠ADB=108°,
∠C =∠B=25° ,
∠A=180°- ∠AEC- ∠C
=180°-108°-25°
=47°
(2)∵ △ABD≌△ACE ,
∴ CE=BD=6cm ,
AE=AD=4cm,
AC=AB=8cm.
(2)若BD=6㎝,AD=4㎝,AB=8cm,你能说出△ACE中各边的长度吗?
1.2 全等三角形
全等三角形
定 义
符号表示
性质
应用
两个能完全重合的三角形叫做全等三角形
对应顶点的字母要写在对应的位置上
全等三角形的对应边相等,对应角相等
对应边、对应角的识别
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
