1.3 探索三角形全等的条件(1) 课件(共14张PPT)
文档属性
| 名称 | 1.3 探索三角形全等的条件(1) 课件(共14张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-04 12:51:30 | ||
图片预览



文档简介
(共14张PPT)
苏科版 八年级上
苏科版 八年级上册
1.3 探索三角形全等的条件(1)
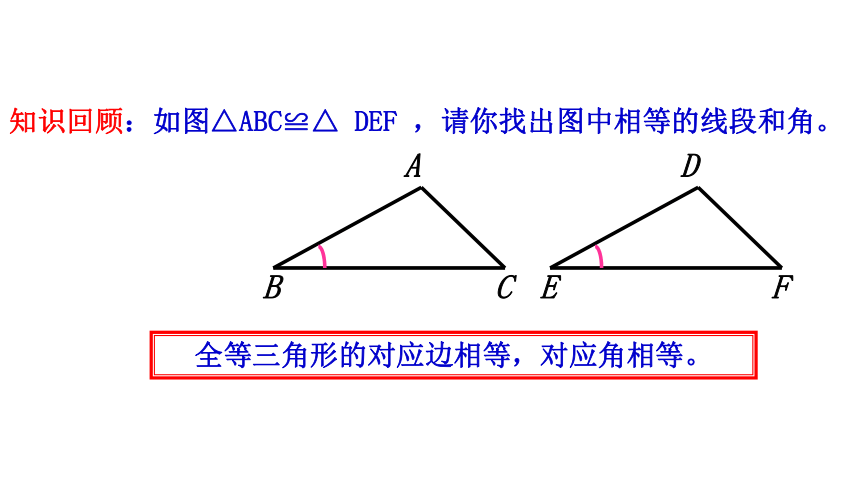
知识回顾:如图△ABC≌△ DEF ,请你找出图中相等的线段和角。
A
B
C
全等三角形的对应边相等,对应角相等。
1.3探索三角形全等的条件(1)
D
E
F
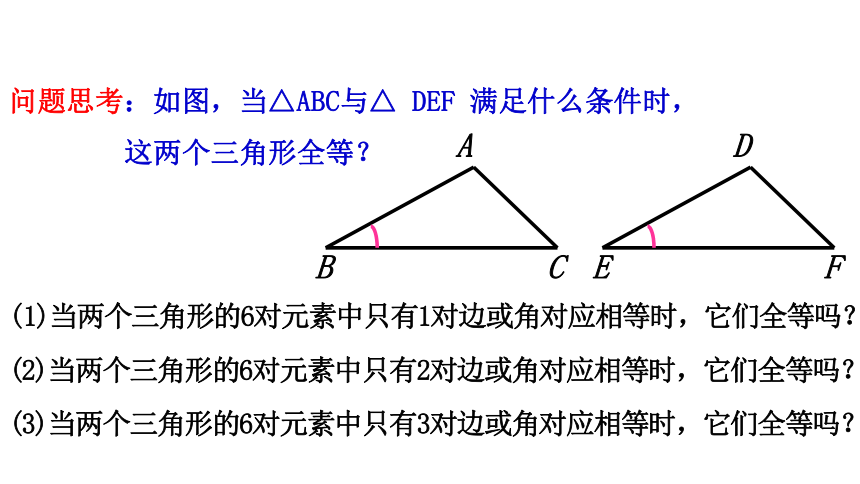
问题思考:如图,当△ABC与△ DEF 满足什么条件时,
这两个三角形全等?
(1)当两个三角形的6对元素中只有1对边或角对应相等时,它们全等吗?
(2)当两个三角形的6对元素中只有2对边或角对应相等时,它们全等吗?
(3)当两个三角形的6对元素中只有3对边或角对应相等时,它们全等吗?
1.3探索三角形全等的条件(1)
A
B
C
D
E
F
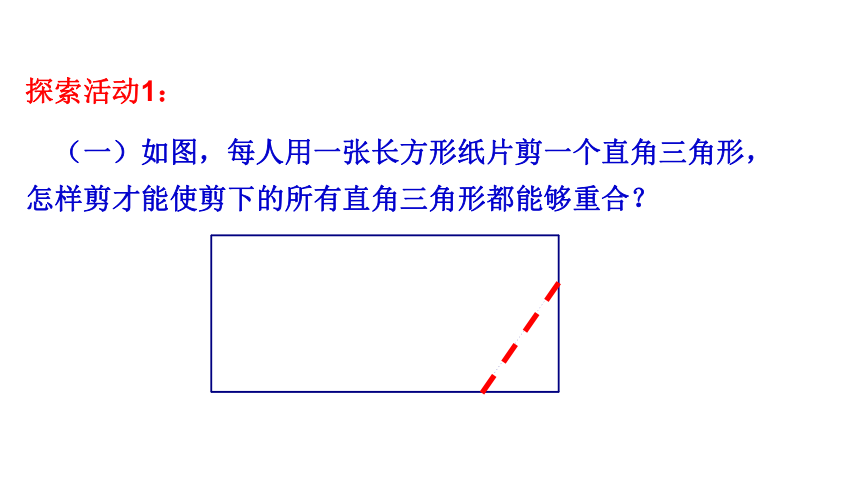
探索活动1:
(一)如图,每人用一张长方形纸片剪一个直角三角形,怎样剪才能使剪下的所有直角三角形都能够重合?
1.3探索三角形全等的条件(1)
如图,△ABC与△DEF、 △MNP 能完全重合吗?
探索活动2:
1.3探索三角形全等的条件(1)
你是如何判断的?
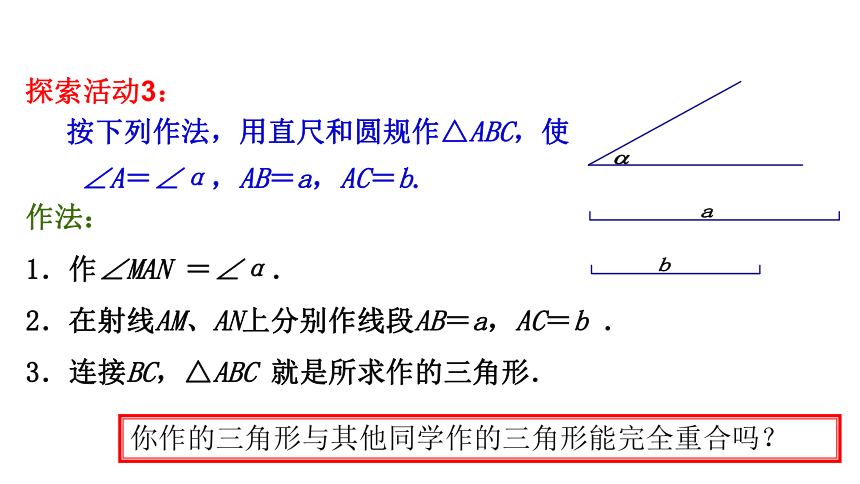
探索活动3:
按下列作法,用直尺和圆规作△ABC,使
∠A=∠α,AB=a,AC=b.
作法:
1.作∠MAN =∠α.
2.在射线AM、AN上分别作线段AB=a,AC=b .
3.连接BC,△ABC 就是所求作的三角形.
你作的三角形与其他同学作的三角形能完全重合吗?
1.3探索三角形全等的条件(1)
基本事实:
两边及其夹角分别相等的两个三角形全等。
(简写成“边角边”或“SAS”) .
几何语言:
∵在△ABC 和△DEF 中,
AB=DE ,
∠B=∠E ,
BC=EF ,
∴ △ABC ≌ △DEF (SAS).
1.3探索三角形全等的条件(1)
找出图中的全等三角形,并说明理由.
新知应用:
例1 如图,AB =AD,∠BAC =∠DAC.
求证:△ABC ≌ △ADC.
证明:在△ABC 和△ADC 中,
AB= AD(已知) ,
∠BAC=∠DAC (已知),
AC=AC(公共边),
∴ △ABC ≌ △ADC(SAS).
1.3探索三角形全等的条件(1)
思考:其中一个三角形经过怎样的图形运动,
可以与另一个三角形重合呢?
指明范围
摆出条件
写出结论
如图,AB =AD,∠BAC =∠DAC.
变式拓展:
求证:(1)DC =BC
(2)CA 平分∠DCB
1.3探索三角形全等的条件(1)
证明:在△ABC 和△ADC 中,
AB= AD(已知) ,
∠BAC=∠DAC (已知),
AC=AC(公共边),
∴ △ABC ≌ △ADC(SAS).
∴ DC=BC (全等三角形的对应边相等)
∠DCA=∠BCA (全等三角形的对应角相等)
即 CA平分∠DCB.
学以致用:
如图,有一池塘,要测池塘两端A、B的距离,可先在平地上取一个可以直接到达A和B的点C,连接AC并延长到D,使CD=CA。连接BC并延长到E,使CE=CB。连接DE,那么量出DE的长就是A、B的距离,为什么?
A
D
C
B
E
1.3探索三角形全等的条件(1)
如图,在△ABC与△ABD中,AB=AB、 ∠B=∠B、AC=AD,
△ABC与△ABD全等吗?
B
A
C
D
注意:SAS中的角必须是两边的夹角,“A”必须在中间。
辨析思考:
如果两个三角形有两组边和一组角相等,那么它们是全等三角形吗?
1.3探索三角形全等的条件(1)
三角形全等的条件
基本事实
几何语言
易错点
两边及其夹角分别相等的两个三角形全等。
SAS中的角必须是两边的夹角。
∵在△ABC 和△DEF 中,
AB=DE,
∠B=∠E,
BC=EF,
∴ △ABC ≌ △DEF (SAS).
1.3探索三角形全等的条件(1)
苏科版 八年级上
苏科版 八年级上册
1.3 探索三角形全等的条件(1)
知识回顾:如图△ABC≌△ DEF ,请你找出图中相等的线段和角。
A
B
C
全等三角形的对应边相等,对应角相等。
1.3探索三角形全等的条件(1)
D
E
F
问题思考:如图,当△ABC与△ DEF 满足什么条件时,
这两个三角形全等?
(1)当两个三角形的6对元素中只有1对边或角对应相等时,它们全等吗?
(2)当两个三角形的6对元素中只有2对边或角对应相等时,它们全等吗?
(3)当两个三角形的6对元素中只有3对边或角对应相等时,它们全等吗?
1.3探索三角形全等的条件(1)
A
B
C
D
E
F
探索活动1:
(一)如图,每人用一张长方形纸片剪一个直角三角形,怎样剪才能使剪下的所有直角三角形都能够重合?
1.3探索三角形全等的条件(1)
如图,△ABC与△DEF、 △MNP 能完全重合吗?
探索活动2:
1.3探索三角形全等的条件(1)
你是如何判断的?
探索活动3:
按下列作法,用直尺和圆规作△ABC,使
∠A=∠α,AB=a,AC=b.
作法:
1.作∠MAN =∠α.
2.在射线AM、AN上分别作线段AB=a,AC=b .
3.连接BC,△ABC 就是所求作的三角形.
你作的三角形与其他同学作的三角形能完全重合吗?
1.3探索三角形全等的条件(1)
基本事实:
两边及其夹角分别相等的两个三角形全等。
(简写成“边角边”或“SAS”) .
几何语言:
∵在△ABC 和△DEF 中,
AB=DE ,
∠B=∠E ,
BC=EF ,
∴ △ABC ≌ △DEF (SAS).
1.3探索三角形全等的条件(1)
找出图中的全等三角形,并说明理由.
新知应用:
例1 如图,AB =AD,∠BAC =∠DAC.
求证:△ABC ≌ △ADC.
证明:在△ABC 和△ADC 中,
AB= AD(已知) ,
∠BAC=∠DAC (已知),
AC=AC(公共边),
∴ △ABC ≌ △ADC(SAS).
1.3探索三角形全等的条件(1)
思考:其中一个三角形经过怎样的图形运动,
可以与另一个三角形重合呢?
指明范围
摆出条件
写出结论
如图,AB =AD,∠BAC =∠DAC.
变式拓展:
求证:(1)DC =BC
(2)CA 平分∠DCB
1.3探索三角形全等的条件(1)
证明:在△ABC 和△ADC 中,
AB= AD(已知) ,
∠BAC=∠DAC (已知),
AC=AC(公共边),
∴ △ABC ≌ △ADC(SAS).
∴ DC=BC (全等三角形的对应边相等)
∠DCA=∠BCA (全等三角形的对应角相等)
即 CA平分∠DCB.
学以致用:
如图,有一池塘,要测池塘两端A、B的距离,可先在平地上取一个可以直接到达A和B的点C,连接AC并延长到D,使CD=CA。连接BC并延长到E,使CE=CB。连接DE,那么量出DE的长就是A、B的距离,为什么?
A
D
C
B
E
1.3探索三角形全等的条件(1)
如图,在△ABC与△ABD中,AB=AB、 ∠B=∠B、AC=AD,
△ABC与△ABD全等吗?
B
A
C
D
注意:SAS中的角必须是两边的夹角,“A”必须在中间。
辨析思考:
如果两个三角形有两组边和一组角相等,那么它们是全等三角形吗?
1.3探索三角形全等的条件(1)
三角形全等的条件
基本事实
几何语言
易错点
两边及其夹角分别相等的两个三角形全等。
SAS中的角必须是两边的夹角。
∵在△ABC 和△DEF 中,
AB=DE,
∠B=∠E,
BC=EF,
∴ △ABC ≌ △DEF (SAS).
1.3探索三角形全等的条件(1)
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
