3[1].6 带电粒子在匀强磁场中的运动 课件(人教版选修3-1)
文档属性
| 名称 | 3[1].6 带电粒子在匀强磁场中的运动 课件(人教版选修3-1) |

|
|
| 格式 | zip | ||
| 文件大小 | 792.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2012-10-14 00:00:00 | ||
图片预览











文档简介
(共43张PPT)
6 带电粒子在匀强磁场中的运动
1.带电粒子在匀强磁场中的运动
(1)洛伦兹力不改变带电粒子速度的________,或者说,洛
伦兹力不对带电粒子________.
(2)沿着与磁场垂直的方向射入磁场的带电粒子,在匀强磁
场中做________________.洛伦兹力总与速度方向________,
正好起到了________的作用.
大小
做功
匀速圆周运动
垂直
向心力
2.基本公式
(1)向心力公式:qvB=__________.
mv2
r
mv
qB
(2)轨道半径公式:r=____________.
3.质谱仪是利用________和________控制电荷运动、测量
带电粒子的________和 ____________的重要工具.
4.回旋加速器利用了电场对带电粒子的______作用和磁场
对运动电荷的______作用来获得高能粒子,这些过程在回旋加
速器的核心部件——____________和其间内的窄缝内完成.
电场
磁场
质量
分析同位素
加速
偏转
两个 D 形盒
知识点 1 带电粒子在匀强磁场中的运动
图 3-6-1
如图 3-6-1 所示,一个质量为 m、带电荷量为 q 的负电
荷 P,以速度 v 垂直进入磁感应强度为 B 的匀强磁场中,曲线
MN 是 P 的运动轨迹的一部分.
(1)由于运动电荷 P 所受的洛伦兹力始终与速度______,不
对运动电荷做功,故运动电荷 P 的速度大小______.
(2)在 MN 中任选很小一段曲线 AB,当 AB 的长度足够短时,
曲线段 AB 可以看成是圆弧的一部分.设圆弧的半径为 r,则 P
从 A 运动到 B 过程中做匀速圆周运动,由圆周运动知识可得 a
=______,而运动电荷 P 只受洛伦兹力作用,所以由洛伦兹力
提供向心力,即____________,可得 R=________,由轨道半
径与周期的关系可得 T=________.
垂直
不变
1.两种常见的运动情况
(1)匀速直线运动:带电粒子的速度方向与磁场方向平行(相
同或相反),此时带电粒子所受洛伦兹力为零,带电粒子做匀速
直线运动.
(2)匀速圆周运动:带电粒子垂直射入匀强磁场,由于洛伦
兹力始终和运动方向垂直,因此不改变速度大小,但是不停地
改变速度方向,所以带电粒子做匀速圆周运动,洛伦兹力提供
匀速圆周运动的向心力.
2.带电粒子做匀速圆周运动的半径和周期
【例 1】如图 3-6-2 所示,匀强磁场磁感应强度为 B=0.2
T,方向垂直纸面向里.在磁场中的 P 点引入一个质量为 m=
2.0×10-8 kg、带电荷量为 q=+5×10-6 C 的粒子,并使之以 v
=10 m/s 的速度垂直于磁场方向开始运动,运动方向如图所示,
不计粒子重力,磁场足够大.
(1)请在图上大致画出粒子做匀速圆周运动的轨迹.
(2)粒子做匀速圆周运动的半径和周期为多大?
图 3-6-2
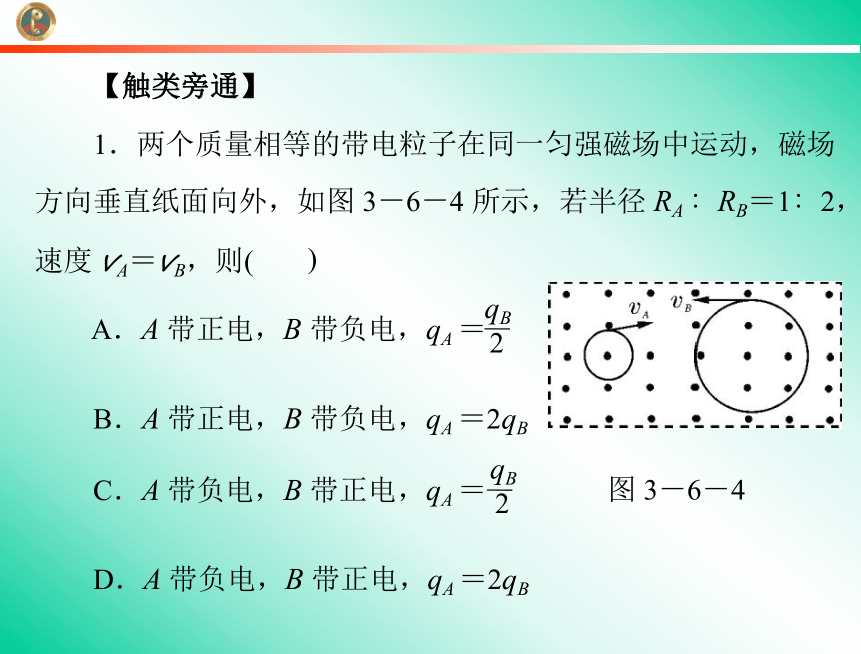
【触类旁通】
1.两个质量相等的带电粒子在同一匀强磁场中运动,磁场
方向垂直纸面向外,如图 3-6-4 所示,若半径 RA ∶RB=1∶2,
速度 vA=vB,则(
)
A.A 带正电,B 带负电,qA =
qB
2
B.A 带正电,B 带负电,qA =2qB
C.A 带负电,B 带正电,qA =
qB
2
图 3-6-4
D.A 带负电,B 带正电,qA =2qB
解析:粒子在匀强磁场中做匀速圆周运动时,洛伦兹力提
供向心力,一定指向圆心,由左手定则可判断,A 带正电,B
带负电;由 R=
mv
Bq
,mA=mB,vA=vB,可得 qA∶qB=RB∶RA
=2∶1,即 qA=2qB,B 正确.
答案:B
知识点 2 质谱仪
1.质谱仪的原理:如图 3-6-5 所示,一个质量为 m、电
图 3-6-5
2.质谱仪的应用:测量带电粒子的质量和分析同位素.
【例 2】(双选)图 3-6-6 是质谱仪的工作原理示意图.带
电粒子被加速电场加速后,进入速度选择器.速度选择器内相
互正交的匀强磁场和匀强电场的强度分别为 B 和 E.平板 S 上有
可让粒子通过的狭缝 P 和记录粒子位置的胶片 A1A2.平板 S 下方
)
有强度为 B0 的匀强磁场.下列表述正确的是(
A.质谱仪是分析同位素的重要工具
B.速度选择器中的磁场方向垂直纸
面向里
C.能通过狭缝 P 的带电粒子的速率
等于
E
B
图 3-6-6
D.粒子打在胶片上的位置越靠近狭缝
P,粒子的荷质比越小
解析:因同位素原子的化学性质完全相同,无法用化学方
法进行分析,故质谱仪就成为同位素分析的重要工具,A 正确.
在速度选择器中,带电粒子所受电场力和洛伦兹力在粒子沿直
线运动时应等大反向,结合左手定则可知 B 错误.再由qE=qvB
错误.
答案:AC
【触类旁通】
2.如图 3-6-7 所示为质谱仪的原理图,A 为粒子加速器;
B 为速度选择器,磁场与电场正交,磁感应强度为 B1,其两板
间的电压为 U2,距离为 d;C 为偏转分离器,磁感应强度为 B2.
现有一质量为 m、电荷量为 q 的正离子经加速后,恰好通过速
度选择器,进入分离器后做半径为 R 的匀速圆周运动,求:
(1)粒子进入偏转分离器的速度 v;
(2)粒子加速器的电压 U1;
(3)粒子在 B2 磁场中做匀速圆周
运动的半径 R.
图 3-6-7
(3)粒子在 B2 中做圆周运动,洛伦兹力提供向心力,有
qvB2=m
v2
R
所以 R=
mU2
qB1B2d
.
知识点 3 回旋加速器
回旋加速器是利用磁场使带电粒子做回旋运动,在运动中
经高频电场反复加速的装置.
图 3-6-8
粒子引出装置
讨论:
(1)回旋加速器的核心部分是放置在磁场中的两个 D 形的金
属扁盒( 如图 3 -6 -8 所示),其基本组成为:①________ ,
②___________________,③_____________,④___________,
⑤__________________.
(2)回旋加速器的基本工作原理是怎样的?
回旋加速器基本工作原理是利用电场对带电粒子的反复加
速和磁场对运动电荷的偏转作用.
粒子源
两个 D 形金属盒
匀强磁场
高频电源
1.回旋加速器的工作原理:利用电场对带电粒子的加速作
用和磁场对运动电荷的偏转作用来获得高能粒子.
2.周期
(1)粒子在 D 形盒中运动的轨道半径每次都不相同,但周期
均相同.
(2)高频电源的周期与带电粒子在 D 形盒中运动的周期相
同,即 T电场=T回旋=
2πm
qB
.
3.最大动能:由 qvB=
粒子在回旋加速器中获得的最大动能与 q、m、B、r 有关,与
加速电压无关.
【例 3】(双选)1932 年劳伦斯制成了世界上第一台回旋加
速器,其原理如图 3-6-9 所示,这台加速器由两个铜质 D 形
)
盒 D1、D2 构成,其间留有空隙,下列说法正确的是(
A.离子由加速器的中心附
近进入加速器
B.离子由加速器的边缘进
入加速器
图 3-6-9
C.离子从磁场中获得能量
D.离子从电场中获得能量
解析:回旋加速器的两个 D 形盒间隙分布周期性变化的电
场,不断地给带电粒子加速使其获得能量;而 D 形盒处分布有
恒定不变的磁场,具有一定速度的带电粒子在 D 形盒内受到磁
场的洛伦兹力提供的向心力而做圆周运动;洛伦兹力不做功,
故不能使离子获得能量,C 错;离子源在回旋加速器的中心附
近.所以正确选项为 A、D.
答案:AD
【触类旁通】
BD
3.(双选)在回旋加速器中,下列说法不正确的是(
)
A.电场用来加速带电粒子,磁场则使带电粒子回旋
B.电场和磁场同时用来加速带电粒子
C.在交流电压一定的条件下,回旋加速器的半径越大,
同一带电粒子获得的动能越大
D.同一带电粒子获得的最大动能只与交流电源的电压大
小有关,而与交流电源的频率无关
1.带电粒子在匀强磁场中圆周运动问题分析
(1)圆心的确定:圆心一定在与速度方向垂直的直线上.
①已知入射方向和出射方向时,可通过入射点和出射点作
垂直于入射方向和出射方向的直线,两条直线的交点就是圆弧
轨道的圆心(如图 3-6-10 甲所示,图中 P 为入射点,M 为出
射点).
②已知入射方向和出射点的位置时,可以通过入射点作入
射方向的垂线,连接入射点和出射点,作其中垂线,这两条垂
线的交点就是圆弧轨道的圆心(如图乙所示,P 为入射点,M 为
出射点).
图 3-6-10
(2)运动半径的确定:作入射点、出射点对应的半径,并作
出相应的辅助三角形,利用三角形的解析方法或其他几何方法,
求解出半径的大小,并与半径公式 r=
mv
qB
联立求解.
(3)粒子运动时间的确定
【例 4】如图 3-6-11 所示,一束电子的电荷量为 e,以
速度 v 垂直射入磁感应强度为 B、宽度为 d 的有界匀强磁场中,
穿过磁场时的速度方向与原来电子的入射方向的夹角θ是 30°,
则电子的质量是多少?电子穿过磁场的时间又是多少?
图 3-6-11
思路点拨:解答本题时可根据以下思路进行:
解:电子在匀强磁场中运动时,只受洛伦兹力作用,故其
轨道是圆弧的一部分.又因洛伦兹力与速度 v 垂直,故圆心应
在电子穿入和穿出时洛伦兹力延长线的交点上.从图中可以看
【触类旁通】
4.上例中若电子的电荷量 e、质量 m、垂直射入磁场的速
度 v、磁场的宽度 d 均已知,磁感应强度 B 大小可调,试求:
(1)要使电子均从磁场右边界射出,磁感应强度 B 应满足的
条件.
(2)电子在磁场中运动的最长时间.
长,tmax=
解:(1)只要电子圆周运动的轨道半径 r>d,电子均从磁场
的右边界射出,由 r=
mv
Be
可得
B=
mv
re
<
mv
de
.
(2)电子在磁场左边界射出时,电子在磁场中运动的时间最
2.带电粒子在复合场中的运动
(1)带电粒子在复合场中常见的运动形式.
①带电粒子在复合场中所受的合外力为零时,粒子静止或
做匀速直线运动
②当带电粒子所受的合外力与运动方向在一条直线上时,
粒子做变速直线运动.
③当带电粒子受到的合外力大小恒定,方向始终和速度方
向垂直时,粒子将做匀速圆周运动.常见的形式是重力和电场
力的合力为零,洛伦兹力充当向心力.
④当带电粒子所受的合外力的大小、方向均不断变化时,
粒子将做变加速运动,此时一般只能用能量观点分析问题.
(2)带电粒子在复合场中运动的分析方法和思路.
①弄清楚复合场的组成.一般是由磁场和电场复合,磁场、
重力场的复合,磁场、重力场、电场的复合,电场和磁场分区
域存在.
②正确进行受力分析.除重力、弹力、摩擦力外要特别关
注电场力和磁场力的分析.
③确定带电粒子的运动状态.注意运动情况和受力情况的
结合进行分析.
④对于粒子连续经过几个不同场的情况,要分段进行分析、
处理.
⑤当带电粒子在复合场中做匀速直线运动时,根据受力平
衡的方程求解.
⑥当带电粒子在复合场中做匀速圆周运动时,应用牛顿运
动定律结合圆周运动进行求解.
⑦当带电粒子做复杂的曲线运动时,一般用功能关系进行
求解.
【例 5】(2012 年揭阳模拟)如图 3-6-12 所示在两极板间
存在匀强电场和磁感应强度为 B 的匀强磁场Ⅰ,一带电量为+
q、质量为 m 的粒子恰能以速度 v 沿 OO1 匀速飞出极板,进入
磁感应强度为 2B 的匀强磁场区域Ⅱ.不计粒子重力,求:
(1)两极板间匀强电场的电场强度的大小和方向.
(2)粒子经过磁场Ⅱ后从左边界射出的位置 S 距 O1 的距离.
图 3-6-12
解:(1)由题可知粒子在极板间受电场力和洛伦兹力平衡,
由粒子带正电可得电场强度方向竖直向上,设大小为E,有qE
=qvB
解得 E=vB.
(2)设粒子经过磁场Ⅱ后从左边界射出的位置 S 距 O1 的距
离为 d.如图 3-6-13,设轨道半径为 R,由几何关系得
d=2R
图 3-6-13
为 ,方向垂直纸面向外的匀强磁场.一质量为m、电荷量为-
【触类旁通】
5.如图 3-6-14 所示,在 x 轴上方有磁感应强度大小为
B,方向垂直纸面向里的匀强磁场.x 轴下方有磁感应强度大小
q 的带电粒子(不计重力),从 x 轴上 O 点以速度 v0 垂直 x 轴向
上射出.求:
(1)射出之后经多长时间粒子
第二次到达 x 轴?
(2)粒子第二次到达 x 轴时离
O 点的距离.
图 3-6-14
解:粒子射出后受洛伦兹力作用做匀速圆周运动,运动半
个圆周后第一次到达 x 轴,以向下的速度 v0 进入下方磁场,又
运动半个圆周后第二次到达 x 轴.如图 10 所示.
图 10
(1)由牛顿第二定律有
6 带电粒子在匀强磁场中的运动
1.带电粒子在匀强磁场中的运动
(1)洛伦兹力不改变带电粒子速度的________,或者说,洛
伦兹力不对带电粒子________.
(2)沿着与磁场垂直的方向射入磁场的带电粒子,在匀强磁
场中做________________.洛伦兹力总与速度方向________,
正好起到了________的作用.
大小
做功
匀速圆周运动
垂直
向心力
2.基本公式
(1)向心力公式:qvB=__________.
mv2
r
mv
qB
(2)轨道半径公式:r=____________.
3.质谱仪是利用________和________控制电荷运动、测量
带电粒子的________和 ____________的重要工具.
4.回旋加速器利用了电场对带电粒子的______作用和磁场
对运动电荷的______作用来获得高能粒子,这些过程在回旋加
速器的核心部件——____________和其间内的窄缝内完成.
电场
磁场
质量
分析同位素
加速
偏转
两个 D 形盒
知识点 1 带电粒子在匀强磁场中的运动
图 3-6-1
如图 3-6-1 所示,一个质量为 m、带电荷量为 q 的负电
荷 P,以速度 v 垂直进入磁感应强度为 B 的匀强磁场中,曲线
MN 是 P 的运动轨迹的一部分.
(1)由于运动电荷 P 所受的洛伦兹力始终与速度______,不
对运动电荷做功,故运动电荷 P 的速度大小______.
(2)在 MN 中任选很小一段曲线 AB,当 AB 的长度足够短时,
曲线段 AB 可以看成是圆弧的一部分.设圆弧的半径为 r,则 P
从 A 运动到 B 过程中做匀速圆周运动,由圆周运动知识可得 a
=______,而运动电荷 P 只受洛伦兹力作用,所以由洛伦兹力
提供向心力,即____________,可得 R=________,由轨道半
径与周期的关系可得 T=________.
垂直
不变
1.两种常见的运动情况
(1)匀速直线运动:带电粒子的速度方向与磁场方向平行(相
同或相反),此时带电粒子所受洛伦兹力为零,带电粒子做匀速
直线运动.
(2)匀速圆周运动:带电粒子垂直射入匀强磁场,由于洛伦
兹力始终和运动方向垂直,因此不改变速度大小,但是不停地
改变速度方向,所以带电粒子做匀速圆周运动,洛伦兹力提供
匀速圆周运动的向心力.
2.带电粒子做匀速圆周运动的半径和周期
【例 1】如图 3-6-2 所示,匀强磁场磁感应强度为 B=0.2
T,方向垂直纸面向里.在磁场中的 P 点引入一个质量为 m=
2.0×10-8 kg、带电荷量为 q=+5×10-6 C 的粒子,并使之以 v
=10 m/s 的速度垂直于磁场方向开始运动,运动方向如图所示,
不计粒子重力,磁场足够大.
(1)请在图上大致画出粒子做匀速圆周运动的轨迹.
(2)粒子做匀速圆周运动的半径和周期为多大?
图 3-6-2
【触类旁通】
1.两个质量相等的带电粒子在同一匀强磁场中运动,磁场
方向垂直纸面向外,如图 3-6-4 所示,若半径 RA ∶RB=1∶2,
速度 vA=vB,则(
)
A.A 带正电,B 带负电,qA =
qB
2
B.A 带正电,B 带负电,qA =2qB
C.A 带负电,B 带正电,qA =
qB
2
图 3-6-4
D.A 带负电,B 带正电,qA =2qB
解析:粒子在匀强磁场中做匀速圆周运动时,洛伦兹力提
供向心力,一定指向圆心,由左手定则可判断,A 带正电,B
带负电;由 R=
mv
Bq
,mA=mB,vA=vB,可得 qA∶qB=RB∶RA
=2∶1,即 qA=2qB,B 正确.
答案:B
知识点 2 质谱仪
1.质谱仪的原理:如图 3-6-5 所示,一个质量为 m、电
图 3-6-5
2.质谱仪的应用:测量带电粒子的质量和分析同位素.
【例 2】(双选)图 3-6-6 是质谱仪的工作原理示意图.带
电粒子被加速电场加速后,进入速度选择器.速度选择器内相
互正交的匀强磁场和匀强电场的强度分别为 B 和 E.平板 S 上有
可让粒子通过的狭缝 P 和记录粒子位置的胶片 A1A2.平板 S 下方
)
有强度为 B0 的匀强磁场.下列表述正确的是(
A.质谱仪是分析同位素的重要工具
B.速度选择器中的磁场方向垂直纸
面向里
C.能通过狭缝 P 的带电粒子的速率
等于
E
B
图 3-6-6
D.粒子打在胶片上的位置越靠近狭缝
P,粒子的荷质比越小
解析:因同位素原子的化学性质完全相同,无法用化学方
法进行分析,故质谱仪就成为同位素分析的重要工具,A 正确.
在速度选择器中,带电粒子所受电场力和洛伦兹力在粒子沿直
线运动时应等大反向,结合左手定则可知 B 错误.再由qE=qvB
错误.
答案:AC
【触类旁通】
2.如图 3-6-7 所示为质谱仪的原理图,A 为粒子加速器;
B 为速度选择器,磁场与电场正交,磁感应强度为 B1,其两板
间的电压为 U2,距离为 d;C 为偏转分离器,磁感应强度为 B2.
现有一质量为 m、电荷量为 q 的正离子经加速后,恰好通过速
度选择器,进入分离器后做半径为 R 的匀速圆周运动,求:
(1)粒子进入偏转分离器的速度 v;
(2)粒子加速器的电压 U1;
(3)粒子在 B2 磁场中做匀速圆周
运动的半径 R.
图 3-6-7
(3)粒子在 B2 中做圆周运动,洛伦兹力提供向心力,有
qvB2=m
v2
R
所以 R=
mU2
qB1B2d
.
知识点 3 回旋加速器
回旋加速器是利用磁场使带电粒子做回旋运动,在运动中
经高频电场反复加速的装置.
图 3-6-8
粒子引出装置
讨论:
(1)回旋加速器的核心部分是放置在磁场中的两个 D 形的金
属扁盒( 如图 3 -6 -8 所示),其基本组成为:①________ ,
②___________________,③_____________,④___________,
⑤__________________.
(2)回旋加速器的基本工作原理是怎样的?
回旋加速器基本工作原理是利用电场对带电粒子的反复加
速和磁场对运动电荷的偏转作用.
粒子源
两个 D 形金属盒
匀强磁场
高频电源
1.回旋加速器的工作原理:利用电场对带电粒子的加速作
用和磁场对运动电荷的偏转作用来获得高能粒子.
2.周期
(1)粒子在 D 形盒中运动的轨道半径每次都不相同,但周期
均相同.
(2)高频电源的周期与带电粒子在 D 形盒中运动的周期相
同,即 T电场=T回旋=
2πm
qB
.
3.最大动能:由 qvB=
粒子在回旋加速器中获得的最大动能与 q、m、B、r 有关,与
加速电压无关.
【例 3】(双选)1932 年劳伦斯制成了世界上第一台回旋加
速器,其原理如图 3-6-9 所示,这台加速器由两个铜质 D 形
)
盒 D1、D2 构成,其间留有空隙,下列说法正确的是(
A.离子由加速器的中心附
近进入加速器
B.离子由加速器的边缘进
入加速器
图 3-6-9
C.离子从磁场中获得能量
D.离子从电场中获得能量
解析:回旋加速器的两个 D 形盒间隙分布周期性变化的电
场,不断地给带电粒子加速使其获得能量;而 D 形盒处分布有
恒定不变的磁场,具有一定速度的带电粒子在 D 形盒内受到磁
场的洛伦兹力提供的向心力而做圆周运动;洛伦兹力不做功,
故不能使离子获得能量,C 错;离子源在回旋加速器的中心附
近.所以正确选项为 A、D.
答案:AD
【触类旁通】
BD
3.(双选)在回旋加速器中,下列说法不正确的是(
)
A.电场用来加速带电粒子,磁场则使带电粒子回旋
B.电场和磁场同时用来加速带电粒子
C.在交流电压一定的条件下,回旋加速器的半径越大,
同一带电粒子获得的动能越大
D.同一带电粒子获得的最大动能只与交流电源的电压大
小有关,而与交流电源的频率无关
1.带电粒子在匀强磁场中圆周运动问题分析
(1)圆心的确定:圆心一定在与速度方向垂直的直线上.
①已知入射方向和出射方向时,可通过入射点和出射点作
垂直于入射方向和出射方向的直线,两条直线的交点就是圆弧
轨道的圆心(如图 3-6-10 甲所示,图中 P 为入射点,M 为出
射点).
②已知入射方向和出射点的位置时,可以通过入射点作入
射方向的垂线,连接入射点和出射点,作其中垂线,这两条垂
线的交点就是圆弧轨道的圆心(如图乙所示,P 为入射点,M 为
出射点).
图 3-6-10
(2)运动半径的确定:作入射点、出射点对应的半径,并作
出相应的辅助三角形,利用三角形的解析方法或其他几何方法,
求解出半径的大小,并与半径公式 r=
mv
qB
联立求解.
(3)粒子运动时间的确定
【例 4】如图 3-6-11 所示,一束电子的电荷量为 e,以
速度 v 垂直射入磁感应强度为 B、宽度为 d 的有界匀强磁场中,
穿过磁场时的速度方向与原来电子的入射方向的夹角θ是 30°,
则电子的质量是多少?电子穿过磁场的时间又是多少?
图 3-6-11
思路点拨:解答本题时可根据以下思路进行:
解:电子在匀强磁场中运动时,只受洛伦兹力作用,故其
轨道是圆弧的一部分.又因洛伦兹力与速度 v 垂直,故圆心应
在电子穿入和穿出时洛伦兹力延长线的交点上.从图中可以看
【触类旁通】
4.上例中若电子的电荷量 e、质量 m、垂直射入磁场的速
度 v、磁场的宽度 d 均已知,磁感应强度 B 大小可调,试求:
(1)要使电子均从磁场右边界射出,磁感应强度 B 应满足的
条件.
(2)电子在磁场中运动的最长时间.
长,tmax=
解:(1)只要电子圆周运动的轨道半径 r>d,电子均从磁场
的右边界射出,由 r=
mv
Be
可得
B=
mv
re
<
mv
de
.
(2)电子在磁场左边界射出时,电子在磁场中运动的时间最
2.带电粒子在复合场中的运动
(1)带电粒子在复合场中常见的运动形式.
①带电粒子在复合场中所受的合外力为零时,粒子静止或
做匀速直线运动
②当带电粒子所受的合外力与运动方向在一条直线上时,
粒子做变速直线运动.
③当带电粒子受到的合外力大小恒定,方向始终和速度方
向垂直时,粒子将做匀速圆周运动.常见的形式是重力和电场
力的合力为零,洛伦兹力充当向心力.
④当带电粒子所受的合外力的大小、方向均不断变化时,
粒子将做变加速运动,此时一般只能用能量观点分析问题.
(2)带电粒子在复合场中运动的分析方法和思路.
①弄清楚复合场的组成.一般是由磁场和电场复合,磁场、
重力场的复合,磁场、重力场、电场的复合,电场和磁场分区
域存在.
②正确进行受力分析.除重力、弹力、摩擦力外要特别关
注电场力和磁场力的分析.
③确定带电粒子的运动状态.注意运动情况和受力情况的
结合进行分析.
④对于粒子连续经过几个不同场的情况,要分段进行分析、
处理.
⑤当带电粒子在复合场中做匀速直线运动时,根据受力平
衡的方程求解.
⑥当带电粒子在复合场中做匀速圆周运动时,应用牛顿运
动定律结合圆周运动进行求解.
⑦当带电粒子做复杂的曲线运动时,一般用功能关系进行
求解.
【例 5】(2012 年揭阳模拟)如图 3-6-12 所示在两极板间
存在匀强电场和磁感应强度为 B 的匀强磁场Ⅰ,一带电量为+
q、质量为 m 的粒子恰能以速度 v 沿 OO1 匀速飞出极板,进入
磁感应强度为 2B 的匀强磁场区域Ⅱ.不计粒子重力,求:
(1)两极板间匀强电场的电场强度的大小和方向.
(2)粒子经过磁场Ⅱ后从左边界射出的位置 S 距 O1 的距离.
图 3-6-12
解:(1)由题可知粒子在极板间受电场力和洛伦兹力平衡,
由粒子带正电可得电场强度方向竖直向上,设大小为E,有qE
=qvB
解得 E=vB.
(2)设粒子经过磁场Ⅱ后从左边界射出的位置 S 距 O1 的距
离为 d.如图 3-6-13,设轨道半径为 R,由几何关系得
d=2R
图 3-6-13
为 ,方向垂直纸面向外的匀强磁场.一质量为m、电荷量为-
【触类旁通】
5.如图 3-6-14 所示,在 x 轴上方有磁感应强度大小为
B,方向垂直纸面向里的匀强磁场.x 轴下方有磁感应强度大小
q 的带电粒子(不计重力),从 x 轴上 O 点以速度 v0 垂直 x 轴向
上射出.求:
(1)射出之后经多长时间粒子
第二次到达 x 轴?
(2)粒子第二次到达 x 轴时离
O 点的距离.
图 3-6-14
解:粒子射出后受洛伦兹力作用做匀速圆周运动,运动半
个圆周后第一次到达 x 轴,以向下的速度 v0 进入下方磁场,又
运动半个圆周后第二次到达 x 轴.如图 10 所示.
图 10
(1)由牛顿第二定律有
