五年级数学上册 三角形的面积拓展 教学设计(表格式)
文档属性
| 名称 | 五年级数学上册 三角形的面积拓展 教学设计(表格式) |  | |
| 格式 | doc | ||
| 文件大小 | 759.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-03 20:49:19 | ||
图片预览

文档简介
教学设计
授课教师姓名 向雪梅 课题 三角形的面积拓展:《面积相等吗》
知识点来源 口学科:数学 □年级:五年级 口教材版本:北师大版口所属章节:五年级上册第四单元《三角形的面积》内容的拓展课。
设计思路 在《平行四边形面积》和《三角形面积》这两课中,学生探索出平行四边形(三角形)公式后,出现了一组等底等高的平行四边形(三角形),让学生观察并思考:你发现了什么?它们面积相等吗?由于底和高都相等,学生不难得出这组平行四边形(三角形)的面积相等的结论。虽然知道了结论,可是由于形状不一样,这样的平行四边形(三角形)容易误以为面积不相等,学生觉得很奇妙。在课后的练习中遇到此类问题学生表示很感兴趣,有思考性还具有挑战,同时也是他们面积几何学习中的难点,而课堂上只是浅显地渗透了等积变形的规律。基于这些思考,我设计了这节课《面积相等吗》既是对教材知识的延伸,也为学生以后学习其他几何知识奠定基础。
教学设计
内容
教学目的 1.结合“三角形比大小”等情境,自主探究并发现等底等高的三角形的外部及本质特征,能从图形中找出等底等高的三角形;2.通过观察、探索等数学活动,发展了学生的空间观念,培养了学生抽象、类比、推理等数学思维能力。3.学生自主学习、动手操作、探索交流等活动,注重知识之间的联系和内化,对学生的思维训练贯穿于每个环节中,培养他们主动探究的学习能力。 涙
教学重点难点 自主探究并发现等底等高的三角形的外部及本质特征,并能在较复杂的图形中找出面积相等的三角形及“蝴蝶模型”。
教学过程 一、矛盾冲突,激趣导入1.引发思考:两个等底等高的三角形发生争论,它们都觉得自己的面积大!究竟谁的面积大呢?引发学生思考。2.想法验证:学生跃跃欲试,主动想办法来验证谁的面积大,有学生提议我们已经学会了三角形面积计算公式,可以求出来。3.动手操作:学生通过量一量、算一算可以得出结论——两个三角形的底和高都相等,面积相等。
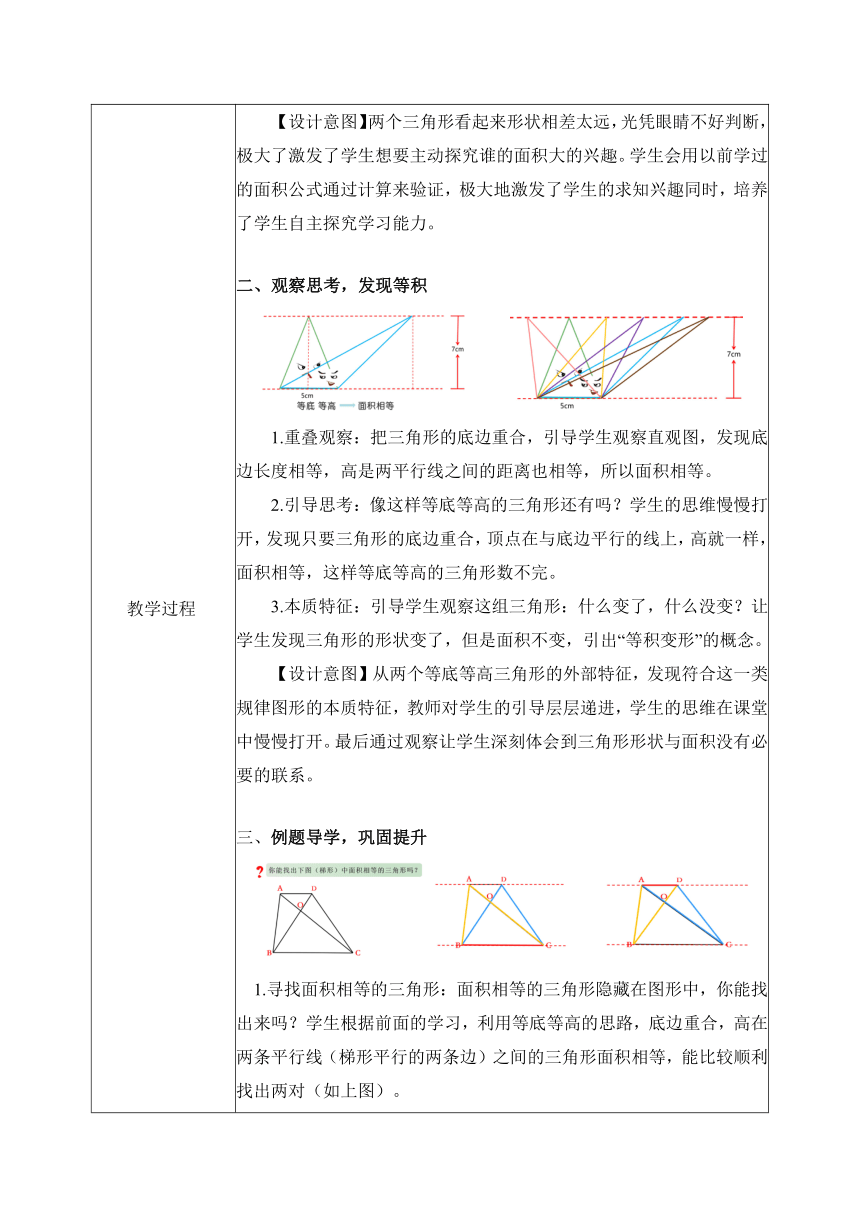
教学过程 【设计意图】两个三角形看起来形状相差太远,光凭眼睛不好判断,极大了激发了学生想要主动探究谁的面积大的兴趣。学生会用以前学过的面积公式通过计算来验证,极大地激发了学生的求知兴趣同时,培养了学生自主探究学习能力。二、观察思考,发现等积1.重叠观察:把三角形的底边重合,引导学生观察直观图,发现底边长度相等,高是两平行线之间的距离也相等,所以面积相等。2.引导思考:像这样等底等高的三角形还有吗?学生的思维慢慢打开,发现只要三角形的底边重合,顶点在与底边平行的线上,高就一样,面积相等,这样等底等高的三角形数不完。3.本质特征:引导学生观察这组三角形:什么变了,什么没变?让学生发现三角形的形状变了,但是面积不变,引出“等积变形”的概念。【设计意图】从两个等底等高三角形的外部特征,发现符合这一类规律图形的本质特征,教师对学生的引导层层递进,学生的思维在课堂中慢慢打开。最后通过观察让学生深刻体会到三角形形状与面积没有必要的联系。三、例题导学,巩固提升1.寻找面积相等的三角形:面积相等的三角形隐藏在图形中,你能找出来吗?学生根据前面的学习,利用等底等高的思路,底边重合,高在两条平行线(梯形平行的两条边)之间的三角形面积相等,能比较顺利找出两对(如上图)。
教学过程 2.发现蝴蝶模型:接着引导学生观察,你还能发现其他面积相等的三角形吗?学生如果有困难可以引导一下,等底等高的三角形有重叠部分,如果同时减去重叠部分,剩下的面积大小如何呢?从而发现了数学中几何中的“蝴蝶模型”。【设计意图】这道例题的设计既能检验学生对前面内容学习掌握的程度,又能极大激发学生的探索挑战欲,隐藏起来一眼看不出的三角形,我都能将它找出来,对自己充满信心。寻找到“蝴蝶模型”为学生提供了寻找图形面积相等的另一个思路,极大地挖掘了学生内在的数学思维能力。四、类比推理,拓展提升1.提问思考:学习完三角形中的等底等高,再过渡到四边形中,三角形中有等底等高的三角形,四边形中有吗?2.观察思考:让学生观察图片中的长方形和平行四边形,学生通过观察发现它们形状不同,由于它们等底等高,所以面积也相等。3.探索其他四边形:数学的教学要严谨,这时候还要继续追问:所有的四边形都满足这个规律吗?学生通过画图、计算、推理等方法,可以验证只有一组对边平行的梯形及两组对边都不平行的四边形不符合,只有平行四边形(包括长方形和正方形)符合。4.平行四边形中的“蝴蝶模型”:体验完平行四边形中的“等积变形”,继续追问:这幅图中你还能找出其他面积相等的图形吗?这个问题会将学生的思路带到“蝴蝶模型”中,通过联想类比发现,在平行四边形中,同时减去重叠部分,剩下部分的面积也相等。
教学过程 【设计意图】从三角形过渡到四边形的设计环节,让学生进一步体验到图形世界中妙不可言的联系。学生将三角形中探索出来的等底等高等面积的知识,直接类比到平行四边形中,既对刚才的三角形知识巩固拓展,又培养了学生自主探究类比推理等数学思维能力。五、回顾交流,课后延伸最后通过回顾交流环节让学生梳理了本节课的知识,注重知识之间的联系和内化,对学生的思维训练贯穿于每个环节中。通过这节课的学习,学生对于“等积变形”规律的认识更加深刻,为以后的几何学习奠定了基础,发展了学生的空间观念,培养了学生抽象、类比、推理等数学思维能力。
授课教师姓名 向雪梅 课题 三角形的面积拓展:《面积相等吗》
知识点来源 口学科:数学 □年级:五年级 口教材版本:北师大版口所属章节:五年级上册第四单元《三角形的面积》内容的拓展课。
设计思路 在《平行四边形面积》和《三角形面积》这两课中,学生探索出平行四边形(三角形)公式后,出现了一组等底等高的平行四边形(三角形),让学生观察并思考:你发现了什么?它们面积相等吗?由于底和高都相等,学生不难得出这组平行四边形(三角形)的面积相等的结论。虽然知道了结论,可是由于形状不一样,这样的平行四边形(三角形)容易误以为面积不相等,学生觉得很奇妙。在课后的练习中遇到此类问题学生表示很感兴趣,有思考性还具有挑战,同时也是他们面积几何学习中的难点,而课堂上只是浅显地渗透了等积变形的规律。基于这些思考,我设计了这节课《面积相等吗》既是对教材知识的延伸,也为学生以后学习其他几何知识奠定基础。
教学设计
内容
教学目的 1.结合“三角形比大小”等情境,自主探究并发现等底等高的三角形的外部及本质特征,能从图形中找出等底等高的三角形;2.通过观察、探索等数学活动,发展了学生的空间观念,培养了学生抽象、类比、推理等数学思维能力。3.学生自主学习、动手操作、探索交流等活动,注重知识之间的联系和内化,对学生的思维训练贯穿于每个环节中,培养他们主动探究的学习能力。 涙
教学重点难点 自主探究并发现等底等高的三角形的外部及本质特征,并能在较复杂的图形中找出面积相等的三角形及“蝴蝶模型”。
教学过程 一、矛盾冲突,激趣导入1.引发思考:两个等底等高的三角形发生争论,它们都觉得自己的面积大!究竟谁的面积大呢?引发学生思考。2.想法验证:学生跃跃欲试,主动想办法来验证谁的面积大,有学生提议我们已经学会了三角形面积计算公式,可以求出来。3.动手操作:学生通过量一量、算一算可以得出结论——两个三角形的底和高都相等,面积相等。
教学过程 【设计意图】两个三角形看起来形状相差太远,光凭眼睛不好判断,极大了激发了学生想要主动探究谁的面积大的兴趣。学生会用以前学过的面积公式通过计算来验证,极大地激发了学生的求知兴趣同时,培养了学生自主探究学习能力。二、观察思考,发现等积1.重叠观察:把三角形的底边重合,引导学生观察直观图,发现底边长度相等,高是两平行线之间的距离也相等,所以面积相等。2.引导思考:像这样等底等高的三角形还有吗?学生的思维慢慢打开,发现只要三角形的底边重合,顶点在与底边平行的线上,高就一样,面积相等,这样等底等高的三角形数不完。3.本质特征:引导学生观察这组三角形:什么变了,什么没变?让学生发现三角形的形状变了,但是面积不变,引出“等积变形”的概念。【设计意图】从两个等底等高三角形的外部特征,发现符合这一类规律图形的本质特征,教师对学生的引导层层递进,学生的思维在课堂中慢慢打开。最后通过观察让学生深刻体会到三角形形状与面积没有必要的联系。三、例题导学,巩固提升1.寻找面积相等的三角形:面积相等的三角形隐藏在图形中,你能找出来吗?学生根据前面的学习,利用等底等高的思路,底边重合,高在两条平行线(梯形平行的两条边)之间的三角形面积相等,能比较顺利找出两对(如上图)。
教学过程 2.发现蝴蝶模型:接着引导学生观察,你还能发现其他面积相等的三角形吗?学生如果有困难可以引导一下,等底等高的三角形有重叠部分,如果同时减去重叠部分,剩下的面积大小如何呢?从而发现了数学中几何中的“蝴蝶模型”。【设计意图】这道例题的设计既能检验学生对前面内容学习掌握的程度,又能极大激发学生的探索挑战欲,隐藏起来一眼看不出的三角形,我都能将它找出来,对自己充满信心。寻找到“蝴蝶模型”为学生提供了寻找图形面积相等的另一个思路,极大地挖掘了学生内在的数学思维能力。四、类比推理,拓展提升1.提问思考:学习完三角形中的等底等高,再过渡到四边形中,三角形中有等底等高的三角形,四边形中有吗?2.观察思考:让学生观察图片中的长方形和平行四边形,学生通过观察发现它们形状不同,由于它们等底等高,所以面积也相等。3.探索其他四边形:数学的教学要严谨,这时候还要继续追问:所有的四边形都满足这个规律吗?学生通过画图、计算、推理等方法,可以验证只有一组对边平行的梯形及两组对边都不平行的四边形不符合,只有平行四边形(包括长方形和正方形)符合。4.平行四边形中的“蝴蝶模型”:体验完平行四边形中的“等积变形”,继续追问:这幅图中你还能找出其他面积相等的图形吗?这个问题会将学生的思路带到“蝴蝶模型”中,通过联想类比发现,在平行四边形中,同时减去重叠部分,剩下部分的面积也相等。
教学过程 【设计意图】从三角形过渡到四边形的设计环节,让学生进一步体验到图形世界中妙不可言的联系。学生将三角形中探索出来的等底等高等面积的知识,直接类比到平行四边形中,既对刚才的三角形知识巩固拓展,又培养了学生自主探究类比推理等数学思维能力。五、回顾交流,课后延伸最后通过回顾交流环节让学生梳理了本节课的知识,注重知识之间的联系和内化,对学生的思维训练贯穿于每个环节中。通过这节课的学习,学生对于“等积变形”规律的认识更加深刻,为以后的几何学习奠定了基础,发展了学生的空间观念,培养了学生抽象、类比、推理等数学思维能力。
同课章节目录
- 一 小数除法
- 1 精打细算
- 2 打扫卫生
- 3 谁打电话的时间长
- 4 人民币兑换
- 5 除得尽吗
- 6 调查“生活垃圾”
- 二 轴对称和平移
- 1 轴对称再认识(一)
- 2 轴对称再认识(二)
- 3 平移
- 4 欣赏与设计
- 三 倍数与因数
- 1 倍数与因数
- 2 探索活动:2、5的倍数的特征
- 3 探索活动:3的倍数的特征
- 4 找因数
- 5 找质数
- 四 多边形的面积
- 1 比较图形的面积
- 2 认识底和高
- 3 探索活动:平行四边形的面积
- 4 探索活动:三角形的面积
- 5 探索活动:梯形的面积
- 五 分数的意义
- 1 分数的再认识(一)
- 2 分数的再认识(二)
- 3 分饼
- 4 分数与除法
- 5 分数基本性质
- 6 找最大的公因数
- 7 约分
- 8 找最小的公倍数
- 9 分数的大小
- 六 组合图形的面积
- 1 组合图形的面积
- 2 探索活动:成长的脚印
- 3 公顷、平方千米
- 数学好玩
- 1 设计秋游方案
- 2 图形中的规律
- 3 尝试与猜测
- 七 可能性
- 1 谁先走
- 2 摸球游戏
