河南省郑州106中学2022届高三上学期11月月考数学(理)试卷(Word版含答案)
文档属性
| 名称 | 河南省郑州106中学2022届高三上学期11月月考数学(理)试卷(Word版含答案) |
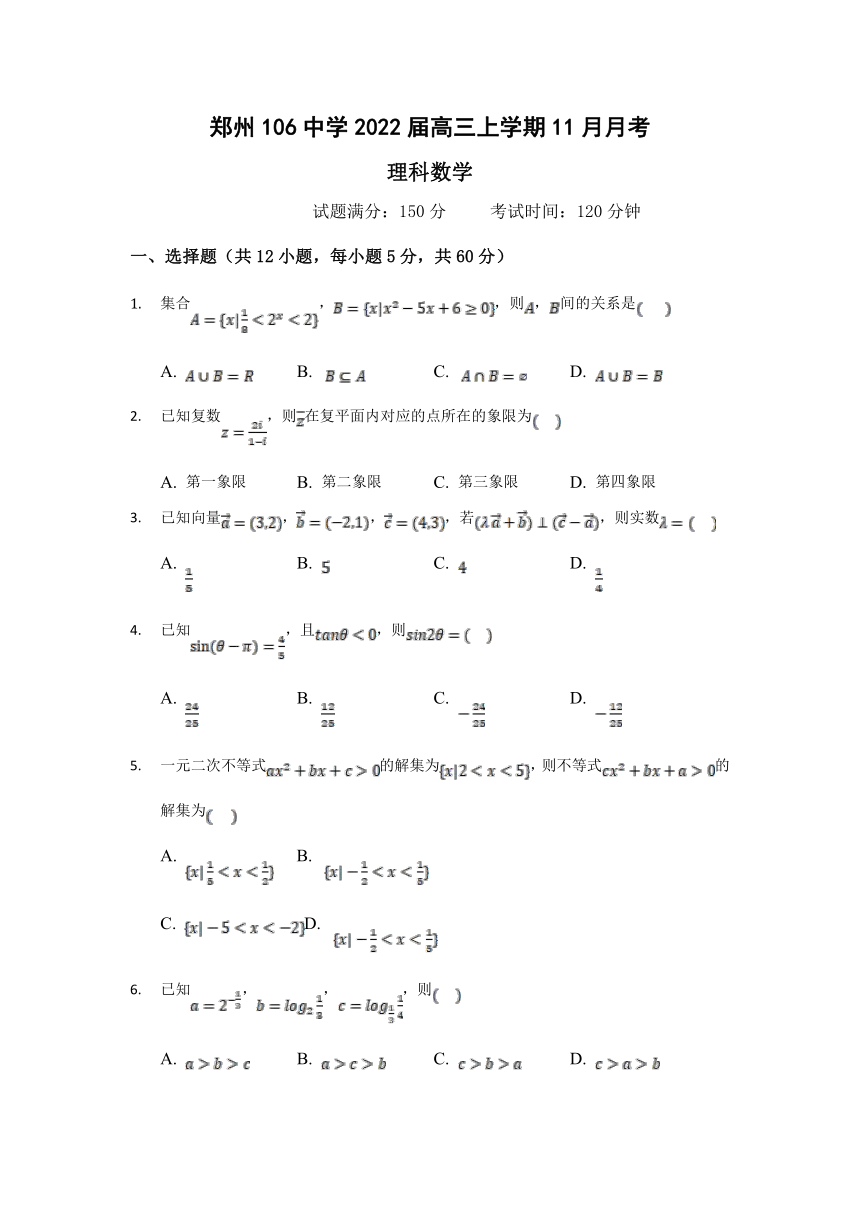
|
|
| 格式 | doc | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-03 00:00:00 | ||
图片预览
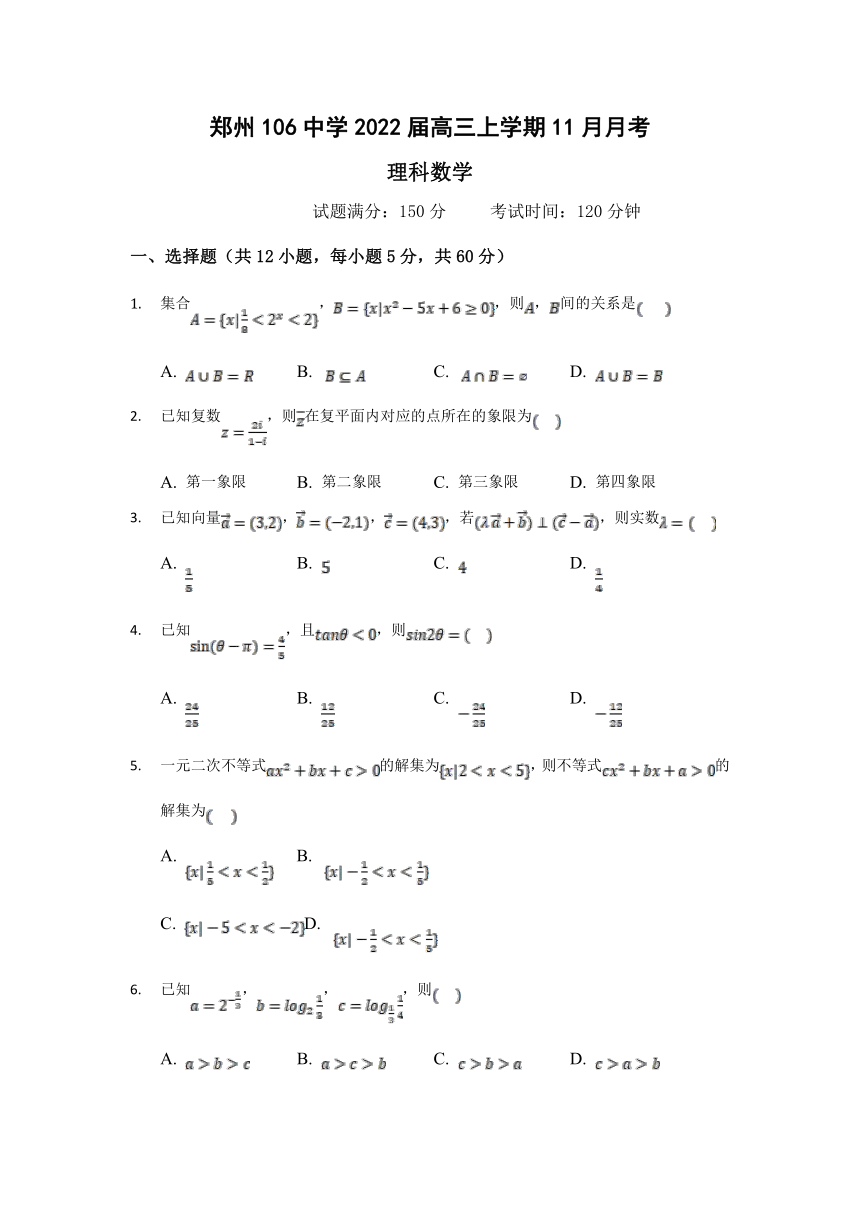




文档简介
郑州106中学2022届高三上学期11月月考
理科数学
试题满分:150分 考试时间:120分钟
一、选择题(共12小题,每小题5分,共60分)
1. 集合,,则,间的关系是
A. B. C. D.
1. 已知复数,则在复平面内对应的点所在的象限为
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
1. 已知向量,,,若,则实数
A. B. C. D.
1. 已知,且,则
A. B. C. D.
1. 一元二次不等式的解集为,则不等式的解集为
A. B.
C. D.
1. 已知,,,则
A. B. C. D.
1. 已知,,,,下列说法正确的是
A. 若,,则 B. 若,,则
C. 若,则 D. 若,则
1. 下列四个命题是真命题的是
A. ,函数都不是偶函数
B. ,,使
C. 向量,,则在的方向上的投影为
D. “”是“”的必要不充分条件
1. 若函数在区间内有唯一的零点,则实数的取值范围是
A. B. C. D.
1. 在等差数列中,,,且,则在中,的最大值为
A. B. C. D.
1. 已知正实数满足,若对任意满足条件的恒成立,
则实数的取值范围是
A. B. C. D.
1. 若不等式恰好有两个整数解,则实数的取值范围是
A. B. C. D.
二、填空题(共4小题,每小题5分,共20分)
1. 若,满足约束条件则的最大值是______.
1. 计算定积分____________
1. 我国古代数学名著九章算术的论割圆术中有:“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周盒体而无所失矣.”它体现了一种无限与有限的转化过程.比如在表达式中“”即代表无限次重复,但原式却是个定值,它可以通过方程,求得,类似上述过程,则______.
1. 设函数的定义域为,为奇函数,为偶函数,当时,若,则
三、解答题(共6小题,共70分)
1. (12分)已知,,.
求的最小正周期及单调递减区间;
求函数在区间上的最大值和最小值.
1. (12分)已知函数.
1求在处的切线方程;
2求的单调区间和极值.
1. (12分)在中,,,分别为内角,,的对边,且.
求角的大小;
若,求的最大值.
1. (12分)已知数列{an}的前n项和为Sn,a1=,2Sn=(n+1)an+1(n≥2).
(1)求{an}的通项公式;
(2)设bn= (n∈N*),数列{bn}的前n项和为Tn,证明:Tn<(n∈N*).
1. (12分)已知函数.
1讨论函数在上的单调性;
2是否存在正实数,使与的图象有唯一一条公切线,若存在,求出的值,若不存在,请说明理由.
选考题:共10分.请考生在第22、23两题中任选一题做答,如果多做,则按所做的第一题记分.
22.[选修4-4:坐标系与参数方程]
直角坐标系中,曲线的参数方程为(为参数),曲线.
(1)在以为极点,轴的正半轴为极轴的极坐标系中,求,的极坐标方程;
(2)射线与异于极点的交点为,与的交点为,求.
23.[选修4-5:不等式选讲]
已知函数.
(1)若恒成立,求实数的最大值;
(2)记(1)中的最大值为,正实数,满足,证明:.
理数答案
一.填空题
1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12.
二.填空题
13. 14. 15. 16.
三.解答题
17.解:,,
由,
的最小正周期,
由,得:,
的单调递减区间为,; ----------6分
由可得:
当时,函数取得最小值为
当时,函数取得最大值为
故得函数在区间上的最大值为,最小值为. ---------12分
18.解:Ⅰ ,,,
所以切线方程为,即. --------------6分
Ⅱ,令,
极小
所以的单调递减区间为,单调递增区间为;
当时,取极小值,极小值为,无极大值.--------12分
19.解:因为,
利用正弦定理可得,,
即, 因为,
所以, 即,
因为, 所以,, 因为,所以.--6分
由及余弦定理可得,
,即,
所以,当且仅当时等号成立,
所以的最大值为.--------------------------------------------------12分
20. (1)因为a1=,2Sn=(n+1)an+1(n≥2),
所以当n=2时,2S2=3a2+1=2(a1+a2),解得a2=2.当n=3时,有2S3=4a3+1,所以a3=3.当n≥3时,2Sn=(n+1)an+1①,2Sn-1=nan-1+1②.由①②两式相减得2an=(n+1)an-nan-1,所以=,
所以==…==1,所以an=--------------------------6分
(2)证明:由(1)得bn==
所以当n=1时,T1=b1=<;
当n≥2时,bn=<=-,
所以Tn<+++…+=-<.
综上,Tn<(n∈N*). -----------------------------12分
21. 解:Ⅰ,
当时,,则在上单调递减;
当时,由得,由得,
函数在上单调递减,在上单调递增;---------------4分
Ⅱ函数在点处的切线方程为,即,
函数在点处的切线方程为,即,
又与的图象有唯一一条公切线,
故,
由得,代入消去,整理得,则此关于的方程有唯一解,
令,令,,
由得,由得,
函数在上单调递增,在上单调递减,则,
当时,方程有唯一解,由得,此时;
当时,二次函数在上显然有一个零点,
时,由方程,可得,
而,则,则,
二次函数在上也有一个零点,不合题意;
综上,. --------------------12
22.
【解析】(1)曲线:(为参数)化为普通方程为,
所以曲线的极坐标方程为,
曲线的极坐标方程为.···········5分
(2)射线与曲线的交点的极径为,
射线与曲线的交点的极径满足,
解得,···········9分
所以.···········10分
23.
【解析】由
得,要使恒成立,
只要,即,实数的最大值为2;·········5分
(2)由(1)知,又,故;
,
∵,∴,
∴. ·····10分
理科数学
试题满分:150分 考试时间:120分钟
一、选择题(共12小题,每小题5分,共60分)
1. 集合,,则,间的关系是
A. B. C. D.
1. 已知复数,则在复平面内对应的点所在的象限为
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
1. 已知向量,,,若,则实数
A. B. C. D.
1. 已知,且,则
A. B. C. D.
1. 一元二次不等式的解集为,则不等式的解集为
A. B.
C. D.
1. 已知,,,则
A. B. C. D.
1. 已知,,,,下列说法正确的是
A. 若,,则 B. 若,,则
C. 若,则 D. 若,则
1. 下列四个命题是真命题的是
A. ,函数都不是偶函数
B. ,,使
C. 向量,,则在的方向上的投影为
D. “”是“”的必要不充分条件
1. 若函数在区间内有唯一的零点,则实数的取值范围是
A. B. C. D.
1. 在等差数列中,,,且,则在中,的最大值为
A. B. C. D.
1. 已知正实数满足,若对任意满足条件的恒成立,
则实数的取值范围是
A. B. C. D.
1. 若不等式恰好有两个整数解,则实数的取值范围是
A. B. C. D.
二、填空题(共4小题,每小题5分,共20分)
1. 若,满足约束条件则的最大值是______.
1. 计算定积分____________
1. 我国古代数学名著九章算术的论割圆术中有:“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周盒体而无所失矣.”它体现了一种无限与有限的转化过程.比如在表达式中“”即代表无限次重复,但原式却是个定值,它可以通过方程,求得,类似上述过程,则______.
1. 设函数的定义域为,为奇函数,为偶函数,当时,若,则
三、解答题(共6小题,共70分)
1. (12分)已知,,.
求的最小正周期及单调递减区间;
求函数在区间上的最大值和最小值.
1. (12分)已知函数.
1求在处的切线方程;
2求的单调区间和极值.
1. (12分)在中,,,分别为内角,,的对边,且.
求角的大小;
若,求的最大值.
1. (12分)已知数列{an}的前n项和为Sn,a1=,2Sn=(n+1)an+1(n≥2).
(1)求{an}的通项公式;
(2)设bn= (n∈N*),数列{bn}的前n项和为Tn,证明:Tn<(n∈N*).
1. (12分)已知函数.
1讨论函数在上的单调性;
2是否存在正实数,使与的图象有唯一一条公切线,若存在,求出的值,若不存在,请说明理由.
选考题:共10分.请考生在第22、23两题中任选一题做答,如果多做,则按所做的第一题记分.
22.[选修4-4:坐标系与参数方程]
直角坐标系中,曲线的参数方程为(为参数),曲线.
(1)在以为极点,轴的正半轴为极轴的极坐标系中,求,的极坐标方程;
(2)射线与异于极点的交点为,与的交点为,求.
23.[选修4-5:不等式选讲]
已知函数.
(1)若恒成立,求实数的最大值;
(2)记(1)中的最大值为,正实数,满足,证明:.
理数答案
一.填空题
1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12.
二.填空题
13. 14. 15. 16.
三.解答题
17.解:,,
由,
的最小正周期,
由,得:,
的单调递减区间为,; ----------6分
由可得:
当时,函数取得最小值为
当时,函数取得最大值为
故得函数在区间上的最大值为,最小值为. ---------12分
18.解:Ⅰ ,,,
所以切线方程为,即. --------------6分
Ⅱ,令,
极小
所以的单调递减区间为,单调递增区间为;
当时,取极小值,极小值为,无极大值.--------12分
19.解:因为,
利用正弦定理可得,,
即, 因为,
所以, 即,
因为, 所以,, 因为,所以.--6分
由及余弦定理可得,
,即,
所以,当且仅当时等号成立,
所以的最大值为.--------------------------------------------------12分
20. (1)因为a1=,2Sn=(n+1)an+1(n≥2),
所以当n=2时,2S2=3a2+1=2(a1+a2),解得a2=2.当n=3时,有2S3=4a3+1,所以a3=3.当n≥3时,2Sn=(n+1)an+1①,2Sn-1=nan-1+1②.由①②两式相减得2an=(n+1)an-nan-1,所以=,
所以==…==1,所以an=--------------------------6分
(2)证明:由(1)得bn==
所以当n=1时,T1=b1=<;
当n≥2时,bn=<=-,
所以Tn<+++…+=-<.
综上,Tn<(n∈N*). -----------------------------12分
21. 解:Ⅰ,
当时,,则在上单调递减;
当时,由得,由得,
函数在上单调递减,在上单调递增;---------------4分
Ⅱ函数在点处的切线方程为,即,
函数在点处的切线方程为,即,
又与的图象有唯一一条公切线,
故,
由得,代入消去,整理得,则此关于的方程有唯一解,
令,令,,
由得,由得,
函数在上单调递增,在上单调递减,则,
当时,方程有唯一解,由得,此时;
当时,二次函数在上显然有一个零点,
时,由方程,可得,
而,则,则,
二次函数在上也有一个零点,不合题意;
综上,. --------------------12
22.
【解析】(1)曲线:(为参数)化为普通方程为,
所以曲线的极坐标方程为,
曲线的极坐标方程为.···········5分
(2)射线与曲线的交点的极径为,
射线与曲线的交点的极径满足,
解得,···········9分
所以.···········10分
23.
【解析】由
得,要使恒成立,
只要,即,实数的最大值为2;·········5分
(2)由(1)知,又,故;
,
∵,∴,
∴. ·····10分
同课章节目录
