2021-2022学年北师大版九年级数学下册3.4圆周角与圆心角的关系 解答题专题训练 (Word版含答案)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学下册3.4圆周角与圆心角的关系 解答题专题训练 (Word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 541.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-04 00:00:00 | ||
图片预览



文档简介
2021-2022学年北师大版九年级数学下册《3.4圆周角与圆心角的关系》
解答题专题训练(附答案)
1.如图,在⊙O中,AB、CD是两条互相垂直的弦,垂足为点E,F为AD的中点,连接FE并延长交BC于点G.
(1)求证:EF=AF;
(2)求证:EF⊥BC.
2.如图,△ABC中,AB=AC,以AB为直径作⊙O,交BC于点D,交CA的延长线于点E,连接AD、DE.
(1)求证:D是BC的中点;
(2)若DE=4,AD=2,求⊙O的半径.
3.如图,AB,CD是⊙O的直径,点F是AD延长线上一点,且CF⊥AB于点E,交⊙O于点G.
(1)求证:∠F=∠FCB.
(2)若FC=6,tan∠F=,求⊙O的直径.
4.如图,AB=AC,AB为⊙O的直径,AC、BC分别交⊙O于点E、D,连接ED、BE.
(1)试判断DE与DC是否相等,并说明理由;
(2)如果BD=2,AE=2,求⊙O的直径.
5.如图,AB是⊙O的直径,C是弧BD的中点,CE⊥AB于E,BD交CE与点F.
(1)求证:CF=BF;
(2)若CD=3,AC=4,求CE的长.
6.如图,在⊙O中,B是⊙O上的一点,∠ABC=120°,弦AC=2,弦BM平分∠ABC交AC于点D,连接MA,MC.
(1)求⊙O半径的长;
(2)试探究线段AB,BC,BM之间的数量关系,并证明你的结论.
7.如图,在⊙O中,AB为⊙O直径,直线MN(在直径AB上方)交⊙O于C、D两点,且MN∥AB,连接CB,DB;点P为直径AB下方⊙O上一点,连接DP,BP.
(1)求证:∠BDC+∠BCN=90°;
(2)若tanP=,⊙O半径为5,求CD的长.
8.如图,在△ACE中,AC=CE,⊙O经过点A,C且与边AE,CE分别交于点D,F,点B是上一点,且,连接AB,BC,CD.
(1)求证:△CDE≌△ABC;
(2)若AC为⊙O的直径,填空:
①当∠E= 时,四边形OCFD为菱形;
②当∠E= 时,四边形ABCD为正方形.
9.如图,△ABC与⊙O交于D,E两点,AB是直径且长为12,OD∥BC.
(1)若∠B=40°,求∠A的度数;
(2)证明:CD=DE;
(3)若AD=4,求CE的长度.
10.如图,AB为⊙O的直径,C、D为圆上的两点,OC∥BD,OC交AD于点E.
(1)求证:AC=CD;
(2)若CE=2,AD=8,求⊙O的半径.
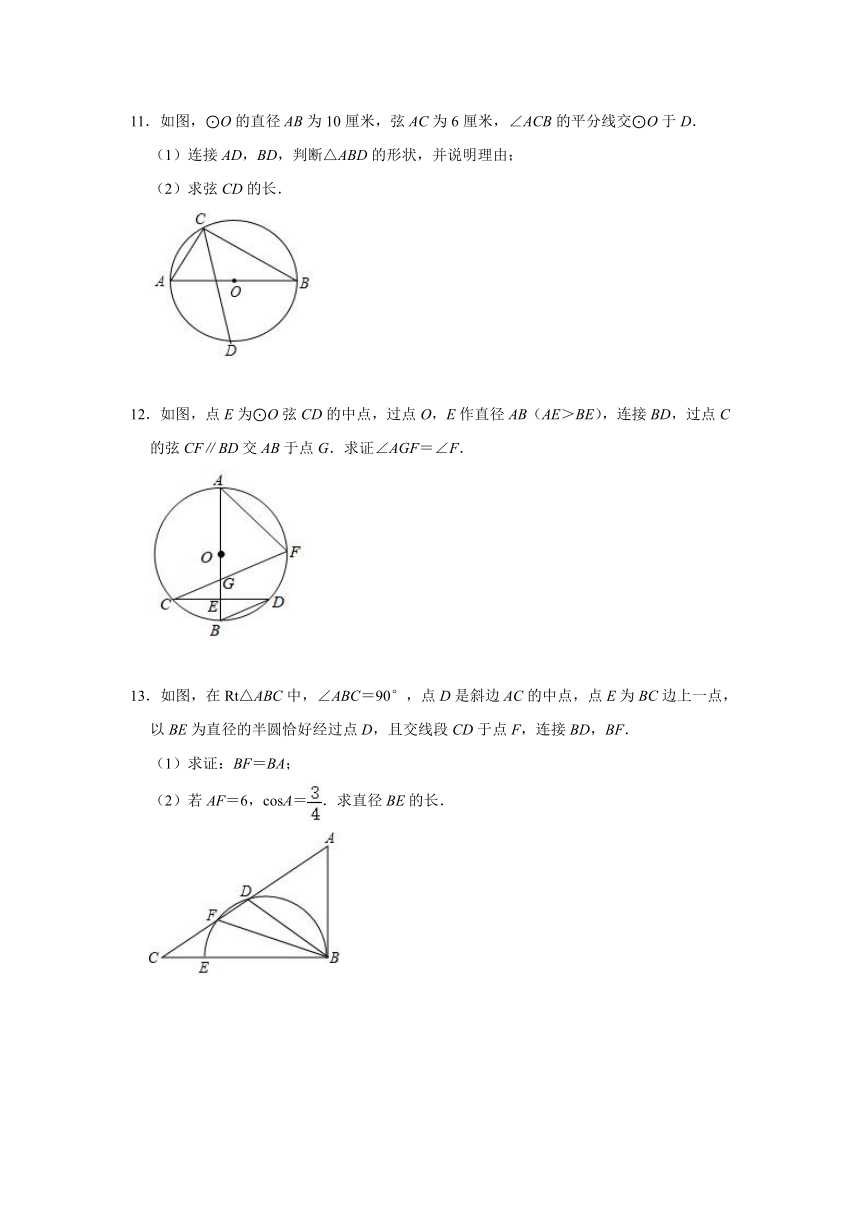
11.如图,⊙O的直径AB为10厘米,弦AC为6厘米,∠ACB的平分线交⊙O于D.
(1)连接AD,BD,判断△ABD的形状,并说明理由;
(2)求弦CD的长.
12.如图,点E为⊙O弦CD的中点,过点O,E作直径AB(AE>BE),连接BD,过点C的弦CF∥BD交AB于点G.求证∠AGF=∠F.
13.如图,在Rt△ABC中,∠ABC=90°,点D是斜边AC的中点,点E为BC边上一点,以BE为直径的半圆恰好经过点D,且交线段CD于点F,连接BD,BF.
(1)求证:BF=BA;
(2)若AF=6,cosA=.求直径BE的长.
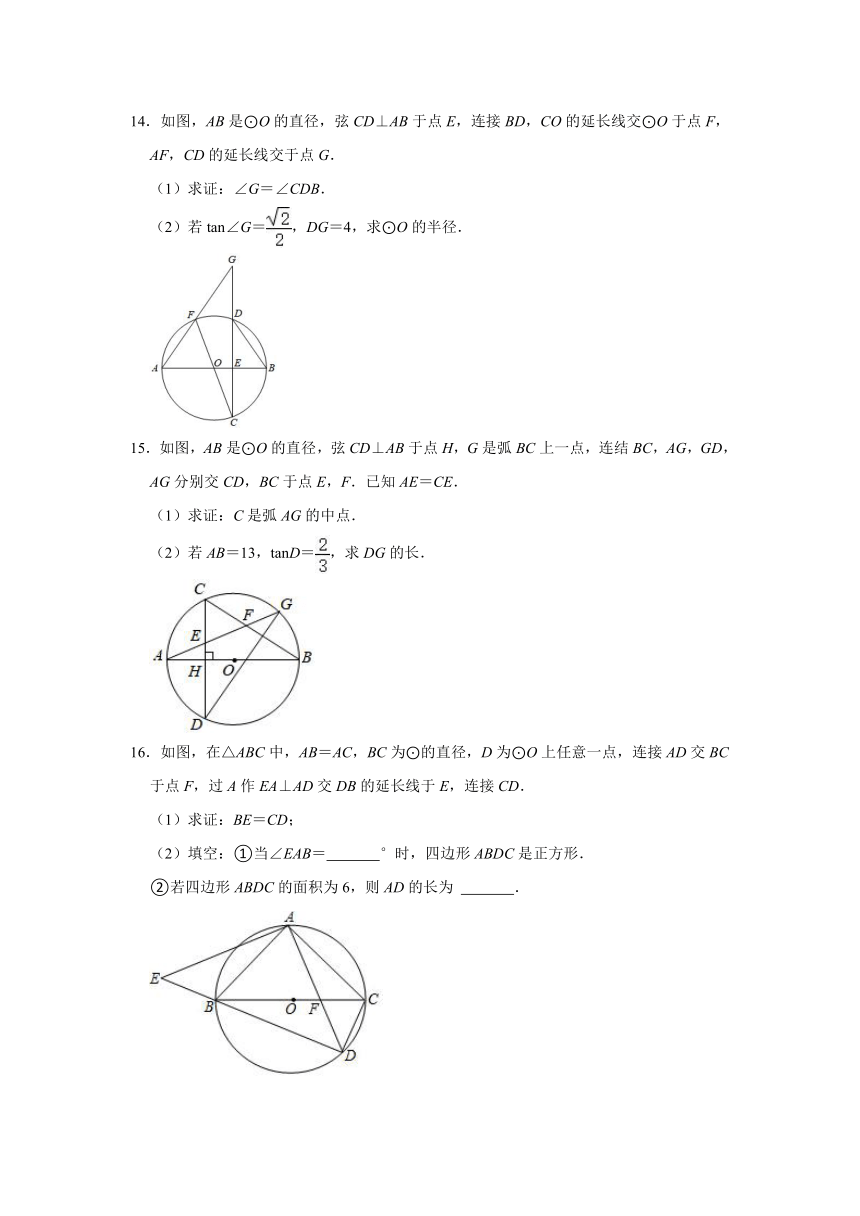
14.如图,AB是⊙O的直径,弦CD⊥AB于点E,连接BD,CO的延长线交⊙O于点F,AF,CD的延长线交于点G.
(1)求证:∠G=∠CDB.
(2)若tan∠G=,DG=4,求⊙O的半径.
15.如图,AB是⊙O的直径,弦CD⊥AB于点H,G是弧BC上一点,连结BC,AG,GD,AG分别交CD,BC于点E,F.已知AE=CE.
(1)求证:C是弧AG的中点.
(2)若AB=13,tanD=,求DG的长.
16.如图,在△ABC中,AB=AC,BC为⊙的直径,D为⊙O上任意一点,连接AD交BC于点F,过A作EA⊥AD交DB的延长线于E,连接CD.
(1)求证:BE=CD;
(2)填空:①当∠EAB= °时,四边形ABDC是正方形.
②若四边形ABDC的面积为6,则AD的长为 .
17.如图,在△ABC中,AB=AC=12,以AC边为直径作⊙O交BC边于点D,过点D作DE⊥AB于点E,ED,AC的延长线交于点F,sin∠CFD=,求线段AE的长.
18.如图,四边形ABCD内接于⊙O,AC为直径,AC和BD交于点E,AB=BC.
(1)求∠ADB的度数;
(2)过B作AD的平行线,交AC于F,试判断线段EA,CF,EF之间满足的等量关系,并说明理由.
19.如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E,过点B作BF⊥AB交AC的延长线于点F.
(1)求证:∠BAC=2∠CBF;
(2)若AB=3,CF=2,求tan∠CBF.
20.如图,在△ABC中,BD⊥AC于D,DC=2AD.以DC为直径作半圆O,交BC于点E,且BD=2BE=2.连接OB,过点D作DF⊥OB交于点F,垂足为G,连接BF.
(1)求⊙O的半径R;
(2)求证:∠DBF=2∠ABD.
参考答案
1.证明:(1)∵AB⊥CD,
∴∠AED=90°,
∵AF=FD,
∴EF=AD=AF.
(2)∵EF=AF,
∴∠A=∠AEF,
∵∠A=∠C,
∴∠AEF=∠C,
∵∠AEF+∠FED=90°,∠FED=∠CEG,
∴∠C+∠CEG=90°,
∴∠CGE=90°,
∴EF⊥BC.
2.(1)证明:∵AB是⊙O直,
∴∠ADB=90°,
∴AD⊥BC,
∵AB=AC,
∴DB=DC,
即点D是BC的中点;
(2)解:∵AB=AC,
∴∠B=∠C,
又∵∠B=∠E,
∴∠C=∠E,
∴DE=DC,
∵DC=BD,DE=4,
∴DE=BD=4,
在Rt△ADB中,AD=2,
AB===2,
∴⊙O 的半径为:=.
3.(1)证明:∵AB,CD是⊙O的直径,
∴∠ACB=∠DAC=90°,
∴AF⊥AC,BC⊥AC,
∴AF∥BC,
∴∠F=∠FCB;
(2)解:∵CF⊥AB,
∴GE=CE,∠ACF+∠BAC=∠ACF+∠F=90°,
∴∠F=∠BAC,
令GE=CE=x,
∵tan∠F=,
∴tan∠BAC==,
∴AE=2x,
∵tan∠F=,
∴EF=4x,
∵FC=6,
∴EF=6﹣x,
∴6﹣x=4x,
∴x=,
即CE=,AE=,
设OC=r,
在Rt△COE中,OC2=OE2+CE2,
即r2=+,
解得,r=,
故⊙O的直径为3.
4.解:(1)DE=DC,理由如下:
连接AD,
∵AB为⊙O的直径,
∴∠ADB=90°,
∴AD⊥BC,
∵AB=AC,
∴∠CAD=∠BAD,DC=BD,
∴=,
∴DE=BD,
∴DE=DC;
(2)∵AB为⊙O的直径,
∴∠AEB=90°,
∵AE=2,
设⊙O的半径为r,
则AB=2r,CE=2r﹣2,
在Rt△ABE中,BE2=AB2﹣AE2,
在Rt△CBE中,BE2=BC2﹣CE2,
∴AB2﹣AE2=BC2﹣CE2,
∵BD=2,BC=2BD,
∴BC=4,
∴(2r)2﹣22=﹣(2r﹣2)2,
∴r=4或r=﹣3(舍去),
∴2r=8,
即⊙O的直径为8.
5.(1)证明:延长CE交⊙O于点M,
∵AB是⊙O的直径,CE⊥AB,
∴=,
∵C是弧BD的中点,
∴=,
∴=,
∴∠1=∠2,
∴CF=BF;
(2)解:∵C是弧BD的中点,CD=3,
∴BC=CD=3,
∵AB是⊙O的直径,
∴∠ACB=90°,
∵AC=4,
∴AB===5,
∵CE⊥AB,
∴AB CE=AC BC,
∴CE===.
6.解:(1)连接OA、OC,过O作OH⊥AC于点H,如图1,
∵∠ABC=120°,
∴∠AMC=180°﹣∠ABC=60°,
∴∠AOC=2∠AMC=120°,
∴∠AOH=∠AOC=60°,
∵AC=2,
∴AH=AC=,
∴OA===2,
故⊙O的半径为2;
(2)AB+BC=BM,理由如下:
在BM上截取BE=BC,连接CE,如图2,
∵∠ABC=120°,BM平分∠ABC,
∴∠ABM=∠CBM=60°,
∵BE=BC,
∴△EBC是等边三角形,
∴CE=CB=BE,∠BCE=60°,
∴∠BCD+∠DCE=60°,
∵∠ACM=60°,
∴∠ECM+∠DCE=60°,
∴∠ECM=∠BCD,
∵∠CAM=∠CBM=60°,∠ACM=∠ABM=60°,
∴△ACM是等边三角形,
∴AC=CM,
∴△ACB≌△MCE(SAS),
∴AB=ME,
∵ME+EB=BM,
∴AB+BC=BM.
7.(1)证明:连接CA.
∵,
∴∠BDC=∠CAB,
∵MN∥AB,
∴∠BCN=∠CBA,
∵AB为⊙O直径,
∴∠ACB=90°,
∴∠CAB+∠CBA=90°,
∴∠BDC+∠BCN=90°.
(2)解:连接AD,过B作BE⊥MN交于E.
∵,
∴∠P=∠DAB,
∵AB=10,
在Rt△ADB中,,
设BD=4x,AD=3x,
∵BD2+AD2=AB2,
∴(4x)2+(3x)2=102,
∴x=2,
∴BD=8,AD=6,
∵∠BDN=∠DBA,∠BDN+∠DBN=∠DBA+∠DAB=90°,
∴∠DBN=∠DAB=∠P,
在Rt△EDB中,,
设DE=4a,BE=3a,DE2+BE2=BD2,
∴(4a)2+(3a)2=82,
∴,
∴,
∵四边形BCDP为圆内接四边形,
∴∠BCD+∠P=180°,∠BCD+∠BCE=180°,
∴∠BCE=∠P.
在Rt△ECB中,,,
∴.
8.证明:(1)∵,
∴∠BAC=∠DCE,
∵∠CDE是圆内接四边形ABCD的外角,
∴∠CDE=∠ABC,
在△CDE和△ABC中,,
∴△CDE≌△ABC(AAS);
(2)如图,①连接AF,
∵AC是直径,
∴OA=OC,∠ADC=∠AFC=90°,
∵四边形OCFD是菱形,
∴DF∥AC,OD∥CE,
∵OA=OC,
∴AD=DE(经过三角形一边的中点平行于一边的直线必平分第三边),
∵DF∥AC,
∴CF=EF(经过三角形一边的中点平行于一边的直线必平分第三边),
∵∠AFC=90°,
∴AC=AE(垂直平分线上的点到两端点的距离相等),
∵AC=CE,
∴AC=AE=CE,
∴△ACE是等边三角形,
∴∠E=60°;
故答案为:60°;
②∵四边形ABCD是正方形,
∴AD=CD,∠ADC=90°,
∴∠ACD=45°,
∵AC=CE,CD⊥AE,
∴∠DCE=∠ACD=45°,
∴∠ACE=90°,
∵AC=CE,
∴△ACE是等腰直角三角形.
∴∠E=45°.
故答案为:45°.
9.(1)解:∵OD∥BC,
∴∠AOD=∠B=40°,
∵OA=OD,
∴∠ADO=∠A,
∴∠A=;
(2)证明:∵四边形ABED内接于⊙O,
∴∠CDE=∠B,∠DEC=∠A,
∴∠CDE=∠AOD,
∵∠C=180°﹣∠CDE﹣∠DEC,
∠ADO=180°﹣∠A﹣∠AOD,
∴∠C=∠ADO=∠A,
∴∠C=∠DEC,
∴CD=DE;
(3)解:连接OE,AE,由(2)得AB=BC=12,
∴∠AOE=2∠B,∠B=∠AOD,
∴∠AOE=2∠AOD,
∴∠AOD=∠DOE,
∴AD=DE,
∴AC=2AD=8,
∵AB是直径:∠AEB=90°,
设CE=x,则BE=12﹣x,
∵AC2﹣CE2=AB2﹣BE2,
∴82﹣x2=122﹣(12﹣x)2,
解得:,
∴CE=.
10.(1)证明:连接AC,CD,
∵OC=OB,
∴∠OBC=∠OCB,
∵OC∥BD,
∴∠OCB=∠CBD,
∴∠OBC=∠CBD,
∴=,
∴AC=CD;
(2)由(1)可知=,
∴OC⊥AD,
又∵AD=8,
∴AE=AD=4,
设⊙O的半径为r,
∵CE=2,
∴OE=r﹣2,
由勾股定理得:AE2+OE2=OA2,
即42+(r﹣2)2=r2,
∴r=5,
∴⊙O的半径为5.
11.解:(1)△ABD为等腰直角三角形;
理由如下:如图,连接AD、BD,
∵AB为直径,
∴∠ACB=∠ADB=90°,
∵CD平分∠ACB,
∴∠ACD=∠BCD=45°,
∴,
∴AD=BD,
∴△ABD为等腰直角三角形;
(2)过A点作AH⊥CD于H,如图,
由 (1)△ABD为等腰直角三角形
∴AD=AB=10=5厘米;
在Rt△ACH中,∵∠ACH=45°,
∴AH=CH=AC=6=3厘米,
在Rt△ADH中,DH==4厘米,
∴CD=CH+DH=34=7厘米.
12.证明:连接AD,
∵AB是⊙O的直径,
∴∠ADB=90°,
即∠ADC+∠BDC=90°,
∵点E为⊙O弦CD的中点,AB是过点E的直径,
∴AB⊥CD,
∴∠B+∠BDC=90°,
∴∠ADC=∠B,
∵CF∥BD,
∴∠AGF=∠B,
∴∠AGF=∠ADC,
由圆周角定理得,∠ADC=∠F,
∴∠AGF=∠F.
13.(1)证明:连接DE,
∵∠ABC=90°,点D是斜边AC的中点,
∴AD=BD,
∴∠A=∠DBA,
∵BE是直径,
∴∠EDB=90°,
∴∠DEB+∠DBE=90°,
∵∠DBA+∠DBE=90°,
∴∠DEB=∠DBA=∠A,
∵∠DEB=∠DFB,
∴∠DFB=∠A,
∴BF=BA;
(2)解:过点B作BH⊥AF于点F,
由(1)知,BF=BA,
∴AH=AF=3,
∵cosA=,
∴AB===4,
∴BH===,
由(1)得,∠DEB=∠A,
∴cos∠DEB=cosA=,
设DE=3x,则BE=4x,BD=x,
∴AD=BD=x,
在Rt△BDH中,BD2=DH2+BH2,
即=+,
解得,x=,
∴BE=4x=.
14.(1)证明:连接AD,
∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠ADC+∠BDE=90°,
∵CD⊥AB,
∴∠BDE+∠ABD=90°,
∴∠ADC=∠ABD,
∵OA=OF,
∴∠GAE=∠AFC=∠ADC,
∵∠ADC=∠AFC,∠GAE+∠G=90°,∠ADC+∠CDB=90°,
∴∠G=∠CDB.
(2)由(1)知,∠G=∠CDB,
∴tan∠CDB=tanG=,
∴=,
设BE=x,则DE=2x,GE=2x+4,
∵=,
∴AE=x+2,
∵∠DAE+∠ADE=90°,∠CDB+∠ADE=90°,
∴∠DAE=∠CDB=∠G,
∴tan∠DAE=,
∴=,
∴=,
∴x=2,
∴AB=AE+BE=x+2+x=6,
∴⊙O的半径为3.
15.(1)证明:连接OC,AC,
∵AB是⊙O的直径,CD⊥AB,
∴=,
∵AE=CE,
∴∠CAE=∠ACE,
∴=,
∴=,
∴C是弧AG的中点;
(2)解:如(1)图,
由(1)得,==,
∴OC⊥AG,∠ACD=∠D,
∵tanD=,
∴tanB=tanD=tan∠ACH=,
∵AB是⊙O的直径,
∴∠ACB=90°,
∵CD⊥AB,
∴==,
∴AH=CH,BH=CH,
∵AB=13,
∴AH+BH=CH+CH=13,
∴CH=6=DH,
∴AH=4,BH=9,
∴AC==2,
∵OC=,
∴cos∠HCO==,
∵∠HCO+∠COA=∠OAE+∠COA=90°,
∴∠HCO=∠OAE,
∴cos∠OAE=cos∠HCO=,
∴tan∠OAE=tan∠HCO=,
∴EH=AH tan∠OAE=4×=,
∴DE=6+=,CE=6﹣=,
∵∠ACD=∠D,
∴AC∥DG,
∴△AEC∽△GED,
∴==,
∴DG=AC=.
16.(1)证明:∵BC为ΘO直径,
∴∠BAC=∠BDC=90°,
∴∠ABD+∠ACD=180°,
又∠ABD+∠ABE=180°,
∴∠ABE=∠ACD,
∵EA⊥AD,
∴∠BAD+∠CAD=∠BAD+∠BAE=90°,
∴∠CAD=∠BAE,
在△ABE和△ACD中,
,
∴△ABE≌△ACD(ASA),
∴BE=CD;
(2)解:①当∠EAB=45°时,四边形ABDC是正方形.
理由:由(1)知,∠EAB=∠CAD,
∴∠CAD=45°,
∴∠BAD=90°﹣45°=45°,
∴=,
∴BD=CD,
∴△ABC,△BCD都是等腰直角三角形,
在△ABC和△DBC中,
,
∴△ABC≌△DBC(ASA),
∴AB=AC=BD=CD,
∴四边形ABDC是菱形,
∵∠BAC=90°,
∴四边形ABDC是正方形.
故答案为:45;
②由(1)知,△ABE≌△ACD,
∴AE=AD,S△ABE=S△ADC,
∴S△AED=S四边形ABDC=6,
∴ AD2=6,
∴AD=2,
故答案为:2.
17.解:连接OD,如图,
∵AB=AC,
∴∠B=∠ACD,
∵OC=OD,
∴∠ODC=∠OCD,
∴∠B=∠ODC,
∴OD∥AB,
∵DE⊥AB
∴OD⊥EF,
∴∠ODF=90°
∵AB=AC=12,
∴OA=OC=OD=6,
在Rt△ODF,sin∠OFD==,
∴OF=10,
∴AF=16,
在Rt△AEF中,∵sin∠AFE==,
∴AE=×16=.
18.解:(1)如图1,
∵AC为直径,
∴∠ABC=90°,
∴∠ACB+∠BAC=90°,
∵AB=BC,
∴∠ACB=∠BAC=45°,
∴∠ADB=∠ACB=45°;
(2)线段EA,CF,EF之间满足的等量关系为:EA2+CF2=EF2.理由如下:
如图2,设∠ABE=α,∠CBF=β,
∵AD∥BF,
∴∠EBF=∠ADB=45°,
又∠ABC=90°,
∴α+β=45°,
过B作BN⊥BE,使BN=BE,连接NC,
∵AB=CB,∠ABE=∠CBN,BE=BN,
∴△AEB≌△CNB(SAS),
∴AE=CN,∠BCN=∠BAE=45°,
∴∠FCN=90°.
∵∠FBN=α+β=∠FBE,BE=BN,BF=BF,
∴△BFE≌△BFN(SAS),
∴EF=FN,
在Rt△NFC中,CF2+CN2=NF2,
∴EA2+CF2=EF2;
19.解:(1)连接AE,
∵AB为⊙O直径,
∴∠AEB=90°,
∵AB=AC,
∴∠BAE=∠BAC,
∵AB为⊙O直径,BF⊥AB,
∴BF是⊙O的切线,
∴∠BAE+∠ABE=∠CBF+∠ABE=90°,
∴∠CBF=∠BAE,
∴∠BAC=2∠CBF;
(2)连接BD,
∵AB为⊙O直径,
∴AF⊥BD,
∴∠BAC+∠ABD=90°,
∵BF⊥AB,
∴∠ABD+∠DBF=90°,
∴∠BAC=∠DBF,
由(1)知∠BAC=2∠CBF,
∴∠DBF=2∠CBF,
∴∠DBC=∠CBF,
∵AB=AC=3,CF=2,
∴AF=AC+CF=5,
在Rt△ABF中,BF===4,
∵ AB BF= AF BD,
∴BD===,
在Rt△DBF中,DF===,
∴CD=DF﹣CF=,
在Rt△DBC中,tan∠DBC===,
∴tan∠CBF=tan∠DBC=.
20.(1)解:连接DE,
∵DC为⊙O的直径,BD⊥AC,
∴∠CED=∠BDC=90°,
∴∠BED=180°﹣90°=90°,
∴∠BED=∠BDC,
又∵∠DBE=∠CBD,
∴△BED∽△BDC,
∴=,
∵BD=2BE=2,
∴BC=4,
在Rt△BDC中,DC2=BC2﹣BD2,
∴DC=2,
即2R=2,
∴R=;
(2)证明:连接DE、OF,
∵OF=OD,OG⊥DF,
∴DG=FG,
在△BGD和△BGF中,
,
∴△BGD≌△BGF(SAS),
∴∠DBO=∠FBO=∠DBF,
∵DC=2AD,DC=2DO,
∴AD=DO,
∵BD⊥AC,
∴BA=BO,
∴BD是△ABO的角平分线,
∴∠ABD=∠DBO,
∴∠DBF=2∠ABD.
解答题专题训练(附答案)
1.如图,在⊙O中,AB、CD是两条互相垂直的弦,垂足为点E,F为AD的中点,连接FE并延长交BC于点G.
(1)求证:EF=AF;
(2)求证:EF⊥BC.
2.如图,△ABC中,AB=AC,以AB为直径作⊙O,交BC于点D,交CA的延长线于点E,连接AD、DE.
(1)求证:D是BC的中点;
(2)若DE=4,AD=2,求⊙O的半径.
3.如图,AB,CD是⊙O的直径,点F是AD延长线上一点,且CF⊥AB于点E,交⊙O于点G.
(1)求证:∠F=∠FCB.
(2)若FC=6,tan∠F=,求⊙O的直径.
4.如图,AB=AC,AB为⊙O的直径,AC、BC分别交⊙O于点E、D,连接ED、BE.
(1)试判断DE与DC是否相等,并说明理由;
(2)如果BD=2,AE=2,求⊙O的直径.
5.如图,AB是⊙O的直径,C是弧BD的中点,CE⊥AB于E,BD交CE与点F.
(1)求证:CF=BF;
(2)若CD=3,AC=4,求CE的长.
6.如图,在⊙O中,B是⊙O上的一点,∠ABC=120°,弦AC=2,弦BM平分∠ABC交AC于点D,连接MA,MC.
(1)求⊙O半径的长;
(2)试探究线段AB,BC,BM之间的数量关系,并证明你的结论.
7.如图,在⊙O中,AB为⊙O直径,直线MN(在直径AB上方)交⊙O于C、D两点,且MN∥AB,连接CB,DB;点P为直径AB下方⊙O上一点,连接DP,BP.
(1)求证:∠BDC+∠BCN=90°;
(2)若tanP=,⊙O半径为5,求CD的长.
8.如图,在△ACE中,AC=CE,⊙O经过点A,C且与边AE,CE分别交于点D,F,点B是上一点,且,连接AB,BC,CD.
(1)求证:△CDE≌△ABC;
(2)若AC为⊙O的直径,填空:
①当∠E= 时,四边形OCFD为菱形;
②当∠E= 时,四边形ABCD为正方形.
9.如图,△ABC与⊙O交于D,E两点,AB是直径且长为12,OD∥BC.
(1)若∠B=40°,求∠A的度数;
(2)证明:CD=DE;
(3)若AD=4,求CE的长度.
10.如图,AB为⊙O的直径,C、D为圆上的两点,OC∥BD,OC交AD于点E.
(1)求证:AC=CD;
(2)若CE=2,AD=8,求⊙O的半径.
11.如图,⊙O的直径AB为10厘米,弦AC为6厘米,∠ACB的平分线交⊙O于D.
(1)连接AD,BD,判断△ABD的形状,并说明理由;
(2)求弦CD的长.
12.如图,点E为⊙O弦CD的中点,过点O,E作直径AB(AE>BE),连接BD,过点C的弦CF∥BD交AB于点G.求证∠AGF=∠F.
13.如图,在Rt△ABC中,∠ABC=90°,点D是斜边AC的中点,点E为BC边上一点,以BE为直径的半圆恰好经过点D,且交线段CD于点F,连接BD,BF.
(1)求证:BF=BA;
(2)若AF=6,cosA=.求直径BE的长.
14.如图,AB是⊙O的直径,弦CD⊥AB于点E,连接BD,CO的延长线交⊙O于点F,AF,CD的延长线交于点G.
(1)求证:∠G=∠CDB.
(2)若tan∠G=,DG=4,求⊙O的半径.
15.如图,AB是⊙O的直径,弦CD⊥AB于点H,G是弧BC上一点,连结BC,AG,GD,AG分别交CD,BC于点E,F.已知AE=CE.
(1)求证:C是弧AG的中点.
(2)若AB=13,tanD=,求DG的长.
16.如图,在△ABC中,AB=AC,BC为⊙的直径,D为⊙O上任意一点,连接AD交BC于点F,过A作EA⊥AD交DB的延长线于E,连接CD.
(1)求证:BE=CD;
(2)填空:①当∠EAB= °时,四边形ABDC是正方形.
②若四边形ABDC的面积为6,则AD的长为 .
17.如图,在△ABC中,AB=AC=12,以AC边为直径作⊙O交BC边于点D,过点D作DE⊥AB于点E,ED,AC的延长线交于点F,sin∠CFD=,求线段AE的长.
18.如图,四边形ABCD内接于⊙O,AC为直径,AC和BD交于点E,AB=BC.
(1)求∠ADB的度数;
(2)过B作AD的平行线,交AC于F,试判断线段EA,CF,EF之间满足的等量关系,并说明理由.
19.如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E,过点B作BF⊥AB交AC的延长线于点F.
(1)求证:∠BAC=2∠CBF;
(2)若AB=3,CF=2,求tan∠CBF.
20.如图,在△ABC中,BD⊥AC于D,DC=2AD.以DC为直径作半圆O,交BC于点E,且BD=2BE=2.连接OB,过点D作DF⊥OB交于点F,垂足为G,连接BF.
(1)求⊙O的半径R;
(2)求证:∠DBF=2∠ABD.
参考答案
1.证明:(1)∵AB⊥CD,
∴∠AED=90°,
∵AF=FD,
∴EF=AD=AF.
(2)∵EF=AF,
∴∠A=∠AEF,
∵∠A=∠C,
∴∠AEF=∠C,
∵∠AEF+∠FED=90°,∠FED=∠CEG,
∴∠C+∠CEG=90°,
∴∠CGE=90°,
∴EF⊥BC.
2.(1)证明:∵AB是⊙O直,
∴∠ADB=90°,
∴AD⊥BC,
∵AB=AC,
∴DB=DC,
即点D是BC的中点;
(2)解:∵AB=AC,
∴∠B=∠C,
又∵∠B=∠E,
∴∠C=∠E,
∴DE=DC,
∵DC=BD,DE=4,
∴DE=BD=4,
在Rt△ADB中,AD=2,
AB===2,
∴⊙O 的半径为:=.
3.(1)证明:∵AB,CD是⊙O的直径,
∴∠ACB=∠DAC=90°,
∴AF⊥AC,BC⊥AC,
∴AF∥BC,
∴∠F=∠FCB;
(2)解:∵CF⊥AB,
∴GE=CE,∠ACF+∠BAC=∠ACF+∠F=90°,
∴∠F=∠BAC,
令GE=CE=x,
∵tan∠F=,
∴tan∠BAC==,
∴AE=2x,
∵tan∠F=,
∴EF=4x,
∵FC=6,
∴EF=6﹣x,
∴6﹣x=4x,
∴x=,
即CE=,AE=,
设OC=r,
在Rt△COE中,OC2=OE2+CE2,
即r2=+,
解得,r=,
故⊙O的直径为3.
4.解:(1)DE=DC,理由如下:
连接AD,
∵AB为⊙O的直径,
∴∠ADB=90°,
∴AD⊥BC,
∵AB=AC,
∴∠CAD=∠BAD,DC=BD,
∴=,
∴DE=BD,
∴DE=DC;
(2)∵AB为⊙O的直径,
∴∠AEB=90°,
∵AE=2,
设⊙O的半径为r,
则AB=2r,CE=2r﹣2,
在Rt△ABE中,BE2=AB2﹣AE2,
在Rt△CBE中,BE2=BC2﹣CE2,
∴AB2﹣AE2=BC2﹣CE2,
∵BD=2,BC=2BD,
∴BC=4,
∴(2r)2﹣22=﹣(2r﹣2)2,
∴r=4或r=﹣3(舍去),
∴2r=8,
即⊙O的直径为8.
5.(1)证明:延长CE交⊙O于点M,
∵AB是⊙O的直径,CE⊥AB,
∴=,
∵C是弧BD的中点,
∴=,
∴=,
∴∠1=∠2,
∴CF=BF;
(2)解:∵C是弧BD的中点,CD=3,
∴BC=CD=3,
∵AB是⊙O的直径,
∴∠ACB=90°,
∵AC=4,
∴AB===5,
∵CE⊥AB,
∴AB CE=AC BC,
∴CE===.
6.解:(1)连接OA、OC,过O作OH⊥AC于点H,如图1,
∵∠ABC=120°,
∴∠AMC=180°﹣∠ABC=60°,
∴∠AOC=2∠AMC=120°,
∴∠AOH=∠AOC=60°,
∵AC=2,
∴AH=AC=,
∴OA===2,
故⊙O的半径为2;
(2)AB+BC=BM,理由如下:
在BM上截取BE=BC,连接CE,如图2,
∵∠ABC=120°,BM平分∠ABC,
∴∠ABM=∠CBM=60°,
∵BE=BC,
∴△EBC是等边三角形,
∴CE=CB=BE,∠BCE=60°,
∴∠BCD+∠DCE=60°,
∵∠ACM=60°,
∴∠ECM+∠DCE=60°,
∴∠ECM=∠BCD,
∵∠CAM=∠CBM=60°,∠ACM=∠ABM=60°,
∴△ACM是等边三角形,
∴AC=CM,
∴△ACB≌△MCE(SAS),
∴AB=ME,
∵ME+EB=BM,
∴AB+BC=BM.
7.(1)证明:连接CA.
∵,
∴∠BDC=∠CAB,
∵MN∥AB,
∴∠BCN=∠CBA,
∵AB为⊙O直径,
∴∠ACB=90°,
∴∠CAB+∠CBA=90°,
∴∠BDC+∠BCN=90°.
(2)解:连接AD,过B作BE⊥MN交于E.
∵,
∴∠P=∠DAB,
∵AB=10,
在Rt△ADB中,,
设BD=4x,AD=3x,
∵BD2+AD2=AB2,
∴(4x)2+(3x)2=102,
∴x=2,
∴BD=8,AD=6,
∵∠BDN=∠DBA,∠BDN+∠DBN=∠DBA+∠DAB=90°,
∴∠DBN=∠DAB=∠P,
在Rt△EDB中,,
设DE=4a,BE=3a,DE2+BE2=BD2,
∴(4a)2+(3a)2=82,
∴,
∴,
∵四边形BCDP为圆内接四边形,
∴∠BCD+∠P=180°,∠BCD+∠BCE=180°,
∴∠BCE=∠P.
在Rt△ECB中,,,
∴.
8.证明:(1)∵,
∴∠BAC=∠DCE,
∵∠CDE是圆内接四边形ABCD的外角,
∴∠CDE=∠ABC,
在△CDE和△ABC中,,
∴△CDE≌△ABC(AAS);
(2)如图,①连接AF,
∵AC是直径,
∴OA=OC,∠ADC=∠AFC=90°,
∵四边形OCFD是菱形,
∴DF∥AC,OD∥CE,
∵OA=OC,
∴AD=DE(经过三角形一边的中点平行于一边的直线必平分第三边),
∵DF∥AC,
∴CF=EF(经过三角形一边的中点平行于一边的直线必平分第三边),
∵∠AFC=90°,
∴AC=AE(垂直平分线上的点到两端点的距离相等),
∵AC=CE,
∴AC=AE=CE,
∴△ACE是等边三角形,
∴∠E=60°;
故答案为:60°;
②∵四边形ABCD是正方形,
∴AD=CD,∠ADC=90°,
∴∠ACD=45°,
∵AC=CE,CD⊥AE,
∴∠DCE=∠ACD=45°,
∴∠ACE=90°,
∵AC=CE,
∴△ACE是等腰直角三角形.
∴∠E=45°.
故答案为:45°.
9.(1)解:∵OD∥BC,
∴∠AOD=∠B=40°,
∵OA=OD,
∴∠ADO=∠A,
∴∠A=;
(2)证明:∵四边形ABED内接于⊙O,
∴∠CDE=∠B,∠DEC=∠A,
∴∠CDE=∠AOD,
∵∠C=180°﹣∠CDE﹣∠DEC,
∠ADO=180°﹣∠A﹣∠AOD,
∴∠C=∠ADO=∠A,
∴∠C=∠DEC,
∴CD=DE;
(3)解:连接OE,AE,由(2)得AB=BC=12,
∴∠AOE=2∠B,∠B=∠AOD,
∴∠AOE=2∠AOD,
∴∠AOD=∠DOE,
∴AD=DE,
∴AC=2AD=8,
∵AB是直径:∠AEB=90°,
设CE=x,则BE=12﹣x,
∵AC2﹣CE2=AB2﹣BE2,
∴82﹣x2=122﹣(12﹣x)2,
解得:,
∴CE=.
10.(1)证明:连接AC,CD,
∵OC=OB,
∴∠OBC=∠OCB,
∵OC∥BD,
∴∠OCB=∠CBD,
∴∠OBC=∠CBD,
∴=,
∴AC=CD;
(2)由(1)可知=,
∴OC⊥AD,
又∵AD=8,
∴AE=AD=4,
设⊙O的半径为r,
∵CE=2,
∴OE=r﹣2,
由勾股定理得:AE2+OE2=OA2,
即42+(r﹣2)2=r2,
∴r=5,
∴⊙O的半径为5.
11.解:(1)△ABD为等腰直角三角形;
理由如下:如图,连接AD、BD,
∵AB为直径,
∴∠ACB=∠ADB=90°,
∵CD平分∠ACB,
∴∠ACD=∠BCD=45°,
∴,
∴AD=BD,
∴△ABD为等腰直角三角形;
(2)过A点作AH⊥CD于H,如图,
由 (1)△ABD为等腰直角三角形
∴AD=AB=10=5厘米;
在Rt△ACH中,∵∠ACH=45°,
∴AH=CH=AC=6=3厘米,
在Rt△ADH中,DH==4厘米,
∴CD=CH+DH=34=7厘米.
12.证明:连接AD,
∵AB是⊙O的直径,
∴∠ADB=90°,
即∠ADC+∠BDC=90°,
∵点E为⊙O弦CD的中点,AB是过点E的直径,
∴AB⊥CD,
∴∠B+∠BDC=90°,
∴∠ADC=∠B,
∵CF∥BD,
∴∠AGF=∠B,
∴∠AGF=∠ADC,
由圆周角定理得,∠ADC=∠F,
∴∠AGF=∠F.
13.(1)证明:连接DE,
∵∠ABC=90°,点D是斜边AC的中点,
∴AD=BD,
∴∠A=∠DBA,
∵BE是直径,
∴∠EDB=90°,
∴∠DEB+∠DBE=90°,
∵∠DBA+∠DBE=90°,
∴∠DEB=∠DBA=∠A,
∵∠DEB=∠DFB,
∴∠DFB=∠A,
∴BF=BA;
(2)解:过点B作BH⊥AF于点F,
由(1)知,BF=BA,
∴AH=AF=3,
∵cosA=,
∴AB===4,
∴BH===,
由(1)得,∠DEB=∠A,
∴cos∠DEB=cosA=,
设DE=3x,则BE=4x,BD=x,
∴AD=BD=x,
在Rt△BDH中,BD2=DH2+BH2,
即=+,
解得,x=,
∴BE=4x=.
14.(1)证明:连接AD,
∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠ADC+∠BDE=90°,
∵CD⊥AB,
∴∠BDE+∠ABD=90°,
∴∠ADC=∠ABD,
∵OA=OF,
∴∠GAE=∠AFC=∠ADC,
∵∠ADC=∠AFC,∠GAE+∠G=90°,∠ADC+∠CDB=90°,
∴∠G=∠CDB.
(2)由(1)知,∠G=∠CDB,
∴tan∠CDB=tanG=,
∴=,
设BE=x,则DE=2x,GE=2x+4,
∵=,
∴AE=x+2,
∵∠DAE+∠ADE=90°,∠CDB+∠ADE=90°,
∴∠DAE=∠CDB=∠G,
∴tan∠DAE=,
∴=,
∴=,
∴x=2,
∴AB=AE+BE=x+2+x=6,
∴⊙O的半径为3.
15.(1)证明:连接OC,AC,
∵AB是⊙O的直径,CD⊥AB,
∴=,
∵AE=CE,
∴∠CAE=∠ACE,
∴=,
∴=,
∴C是弧AG的中点;
(2)解:如(1)图,
由(1)得,==,
∴OC⊥AG,∠ACD=∠D,
∵tanD=,
∴tanB=tanD=tan∠ACH=,
∵AB是⊙O的直径,
∴∠ACB=90°,
∵CD⊥AB,
∴==,
∴AH=CH,BH=CH,
∵AB=13,
∴AH+BH=CH+CH=13,
∴CH=6=DH,
∴AH=4,BH=9,
∴AC==2,
∵OC=,
∴cos∠HCO==,
∵∠HCO+∠COA=∠OAE+∠COA=90°,
∴∠HCO=∠OAE,
∴cos∠OAE=cos∠HCO=,
∴tan∠OAE=tan∠HCO=,
∴EH=AH tan∠OAE=4×=,
∴DE=6+=,CE=6﹣=,
∵∠ACD=∠D,
∴AC∥DG,
∴△AEC∽△GED,
∴==,
∴DG=AC=.
16.(1)证明:∵BC为ΘO直径,
∴∠BAC=∠BDC=90°,
∴∠ABD+∠ACD=180°,
又∠ABD+∠ABE=180°,
∴∠ABE=∠ACD,
∵EA⊥AD,
∴∠BAD+∠CAD=∠BAD+∠BAE=90°,
∴∠CAD=∠BAE,
在△ABE和△ACD中,
,
∴△ABE≌△ACD(ASA),
∴BE=CD;
(2)解:①当∠EAB=45°时,四边形ABDC是正方形.
理由:由(1)知,∠EAB=∠CAD,
∴∠CAD=45°,
∴∠BAD=90°﹣45°=45°,
∴=,
∴BD=CD,
∴△ABC,△BCD都是等腰直角三角形,
在△ABC和△DBC中,
,
∴△ABC≌△DBC(ASA),
∴AB=AC=BD=CD,
∴四边形ABDC是菱形,
∵∠BAC=90°,
∴四边形ABDC是正方形.
故答案为:45;
②由(1)知,△ABE≌△ACD,
∴AE=AD,S△ABE=S△ADC,
∴S△AED=S四边形ABDC=6,
∴ AD2=6,
∴AD=2,
故答案为:2.
17.解:连接OD,如图,
∵AB=AC,
∴∠B=∠ACD,
∵OC=OD,
∴∠ODC=∠OCD,
∴∠B=∠ODC,
∴OD∥AB,
∵DE⊥AB
∴OD⊥EF,
∴∠ODF=90°
∵AB=AC=12,
∴OA=OC=OD=6,
在Rt△ODF,sin∠OFD==,
∴OF=10,
∴AF=16,
在Rt△AEF中,∵sin∠AFE==,
∴AE=×16=.
18.解:(1)如图1,
∵AC为直径,
∴∠ABC=90°,
∴∠ACB+∠BAC=90°,
∵AB=BC,
∴∠ACB=∠BAC=45°,
∴∠ADB=∠ACB=45°;
(2)线段EA,CF,EF之间满足的等量关系为:EA2+CF2=EF2.理由如下:
如图2,设∠ABE=α,∠CBF=β,
∵AD∥BF,
∴∠EBF=∠ADB=45°,
又∠ABC=90°,
∴α+β=45°,
过B作BN⊥BE,使BN=BE,连接NC,
∵AB=CB,∠ABE=∠CBN,BE=BN,
∴△AEB≌△CNB(SAS),
∴AE=CN,∠BCN=∠BAE=45°,
∴∠FCN=90°.
∵∠FBN=α+β=∠FBE,BE=BN,BF=BF,
∴△BFE≌△BFN(SAS),
∴EF=FN,
在Rt△NFC中,CF2+CN2=NF2,
∴EA2+CF2=EF2;
19.解:(1)连接AE,
∵AB为⊙O直径,
∴∠AEB=90°,
∵AB=AC,
∴∠BAE=∠BAC,
∵AB为⊙O直径,BF⊥AB,
∴BF是⊙O的切线,
∴∠BAE+∠ABE=∠CBF+∠ABE=90°,
∴∠CBF=∠BAE,
∴∠BAC=2∠CBF;
(2)连接BD,
∵AB为⊙O直径,
∴AF⊥BD,
∴∠BAC+∠ABD=90°,
∵BF⊥AB,
∴∠ABD+∠DBF=90°,
∴∠BAC=∠DBF,
由(1)知∠BAC=2∠CBF,
∴∠DBF=2∠CBF,
∴∠DBC=∠CBF,
∵AB=AC=3,CF=2,
∴AF=AC+CF=5,
在Rt△ABF中,BF===4,
∵ AB BF= AF BD,
∴BD===,
在Rt△DBF中,DF===,
∴CD=DF﹣CF=,
在Rt△DBC中,tan∠DBC===,
∴tan∠CBF=tan∠DBC=.
20.(1)解:连接DE,
∵DC为⊙O的直径,BD⊥AC,
∴∠CED=∠BDC=90°,
∴∠BED=180°﹣90°=90°,
∴∠BED=∠BDC,
又∵∠DBE=∠CBD,
∴△BED∽△BDC,
∴=,
∵BD=2BE=2,
∴BC=4,
在Rt△BDC中,DC2=BC2﹣BD2,
∴DC=2,
即2R=2,
∴R=;
(2)证明:连接DE、OF,
∵OF=OD,OG⊥DF,
∴DG=FG,
在△BGD和△BGF中,
,
∴△BGD≌△BGF(SAS),
∴∠DBO=∠FBO=∠DBF,
∵DC=2AD,DC=2DO,
∴AD=DO,
∵BD⊥AC,
∴BA=BO,
∴BD是△ABO的角平分线,
∴∠ABD=∠DBO,
∴∠DBF=2∠ABD.
