2021-2022学年北师大版九年级数学下册3.8圆内接正多边形 同步练习题(Word版含答案)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学下册3.8圆内接正多边形 同步练习题(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 425.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-04 20:32:26 | ||
图片预览

文档简介
2021-2022学年北师大版九年级数学下册《3.8圆内接正多边形》同步练习题(附答案)
1.如图,已知正五边形ABCDE中,点F是BC的中点,P是线段EF上的动点,连接AP,BP,当AP+BP的值最小时,∠BPF的度数为( )
A.36° B.45° C.54° D.60°
2.如图,正五边形ABCDE内接于⊙O,则∠DAE的度数是( )
A.36° B.26° C.30° D.45°
3.如图,⊙O是正五边形ABCDE的外接圆,点P为上的一点,则∠APC的度数为( )
A.36° B.60° C.72° D.75°
4.若正六边形的边长为4,则它的外接圆的半径为( )
A.4 B.4 C.2 D.2
5.正十边形的中心角是( )
A.18° B.36° C.72° D.144°
6.已知正六边形的半径为,则此正六边形的面积为( )
A. B.2 C.3 D.4
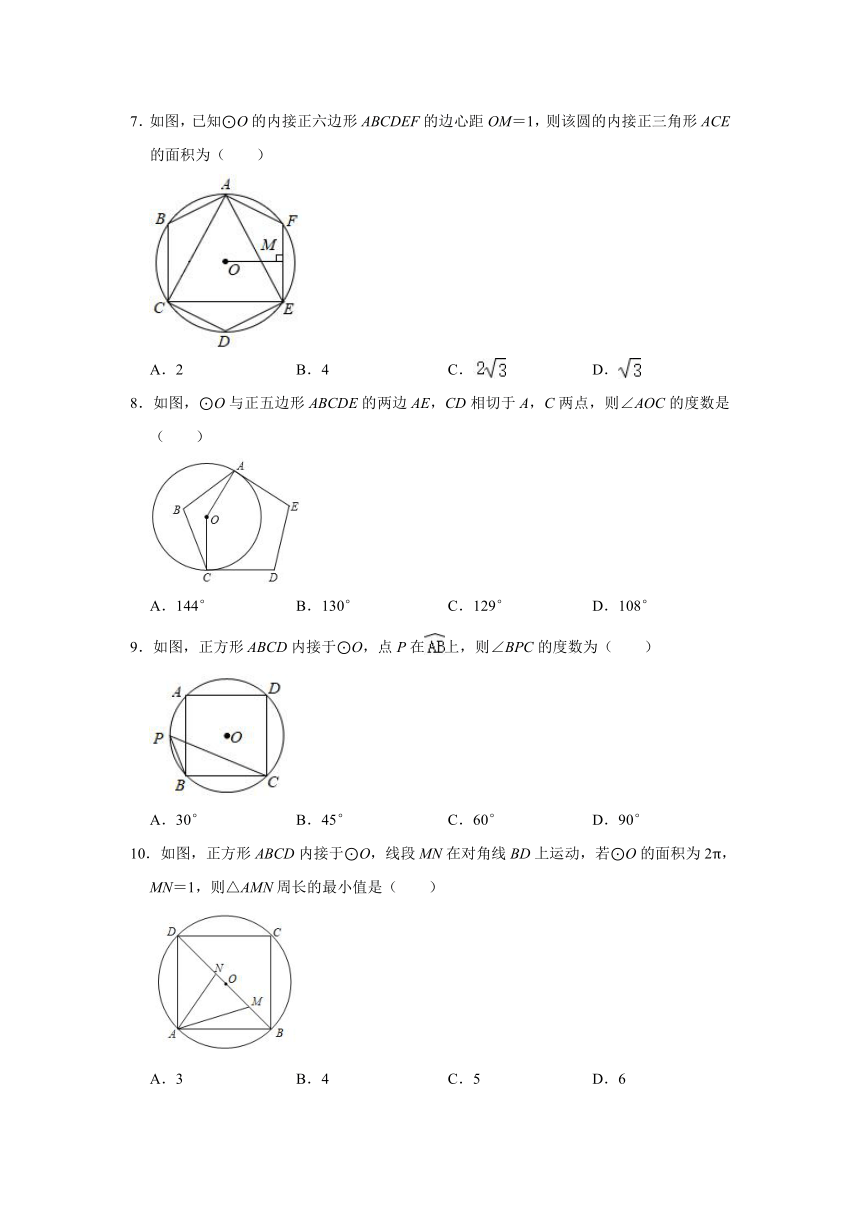
7.如图,已知⊙O的内接正六边形ABCDEF的边心距OM=1,则该圆的内接正三角形ACE的面积为( )
A.2 B.4 C. D.
8.如图,⊙O与正五边形ABCDE的两边AE,CD相切于A,C两点,则∠AOC的度数是( )
A.144° B.130° C.129° D.108°
9.如图,正方形ABCD内接于⊙O,点P在上,则∠BPC的度数为( )
A.30° B.45° C.60° D.90°
10.如图,正方形ABCD内接于⊙O,线段MN在对角线BD上运动,若⊙O的面积为2π,MN=1,则△AMN周长的最小值是( )
A.3 B.4 C.5 D.6
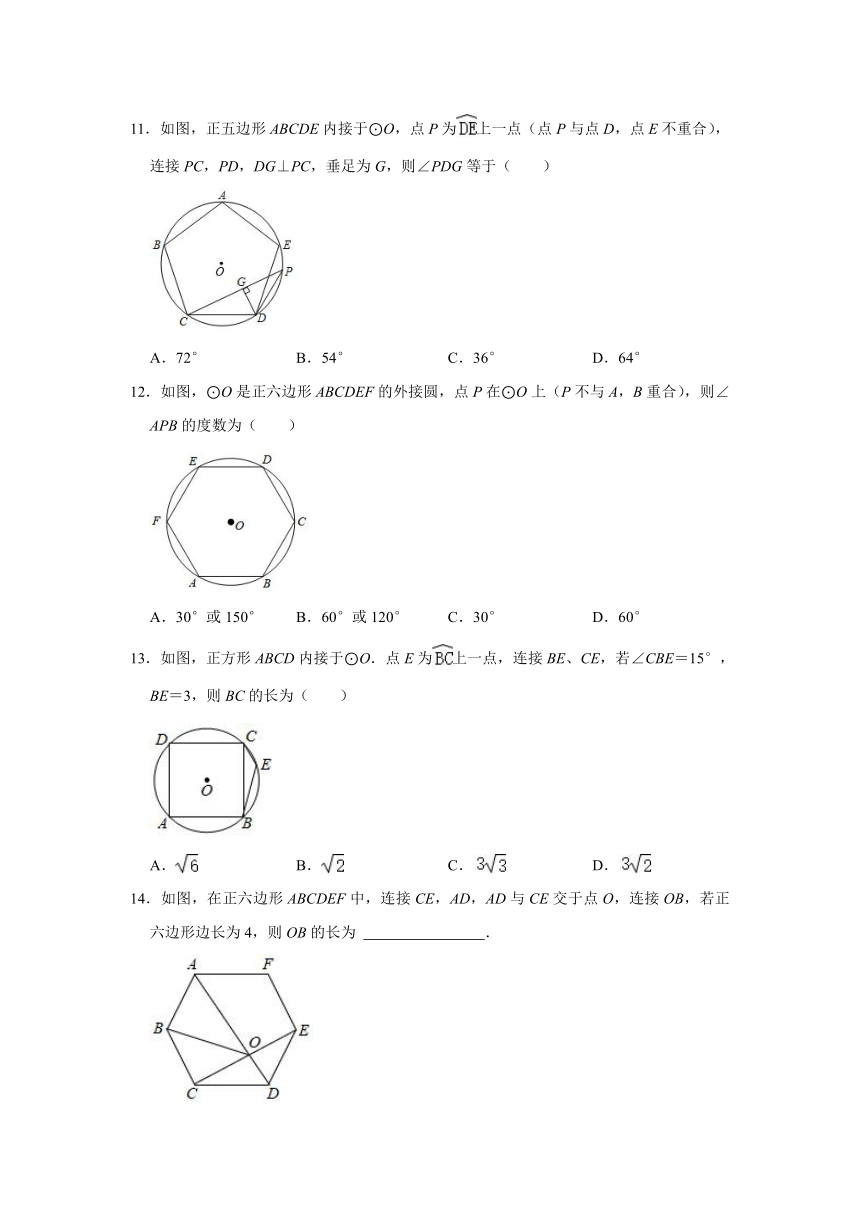
11.如图,正五边形ABCDE内接于⊙O,点P为上一点(点P与点D,点E不重合),连接PC,PD,DG⊥PC,垂足为G,则∠PDG等于( )
A.72° B.54° C.36° D.64°
12.如图,⊙O是正六边形ABCDEF的外接圆,点P在⊙O上(P不与A,B重合),则∠APB的度数为( )
A.30°或150° B.60°或120° C.30° D.60°
13.如图,正方形ABCD内接于⊙O.点E为上一点,连接BE、CE,若∠CBE=15°,BE=3,则BC的长为( )
A. B. C. D.
14.如图,在正六边形ABCDEF中,连接CE,AD,AD与CE交于点O,连接OB,若正六边形边长为4,则OB的长为 .
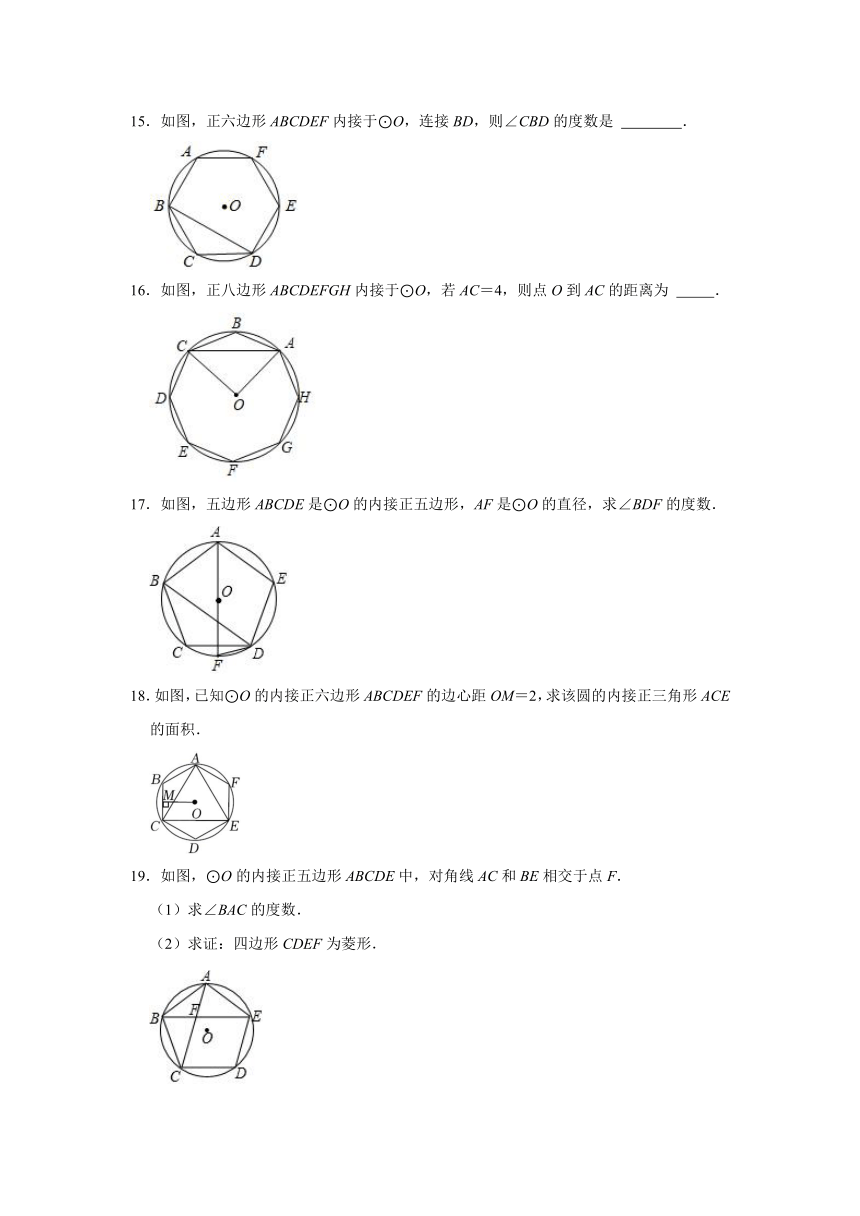
15.如图,正六边形ABCDEF内接于⊙O,连接BD,则∠CBD的度数是 .
16.如图,正八边形ABCDEFGH内接于⊙O,若AC=4,则点O到AC的距离为 .
17.如图,五边形ABCDE是⊙O的内接正五边形,AF是⊙O的直径,求∠BDF的度数.
18.如图,已知⊙O的内接正六边形ABCDEF的边心距OM=2,求该圆的内接正三角形ACE的面积.
19.如图,⊙O的内接正五边形ABCDE中,对角线AC和BE相交于点F.
(1)求∠BAC的度数.
(2)求证:四边形CDEF为菱形.
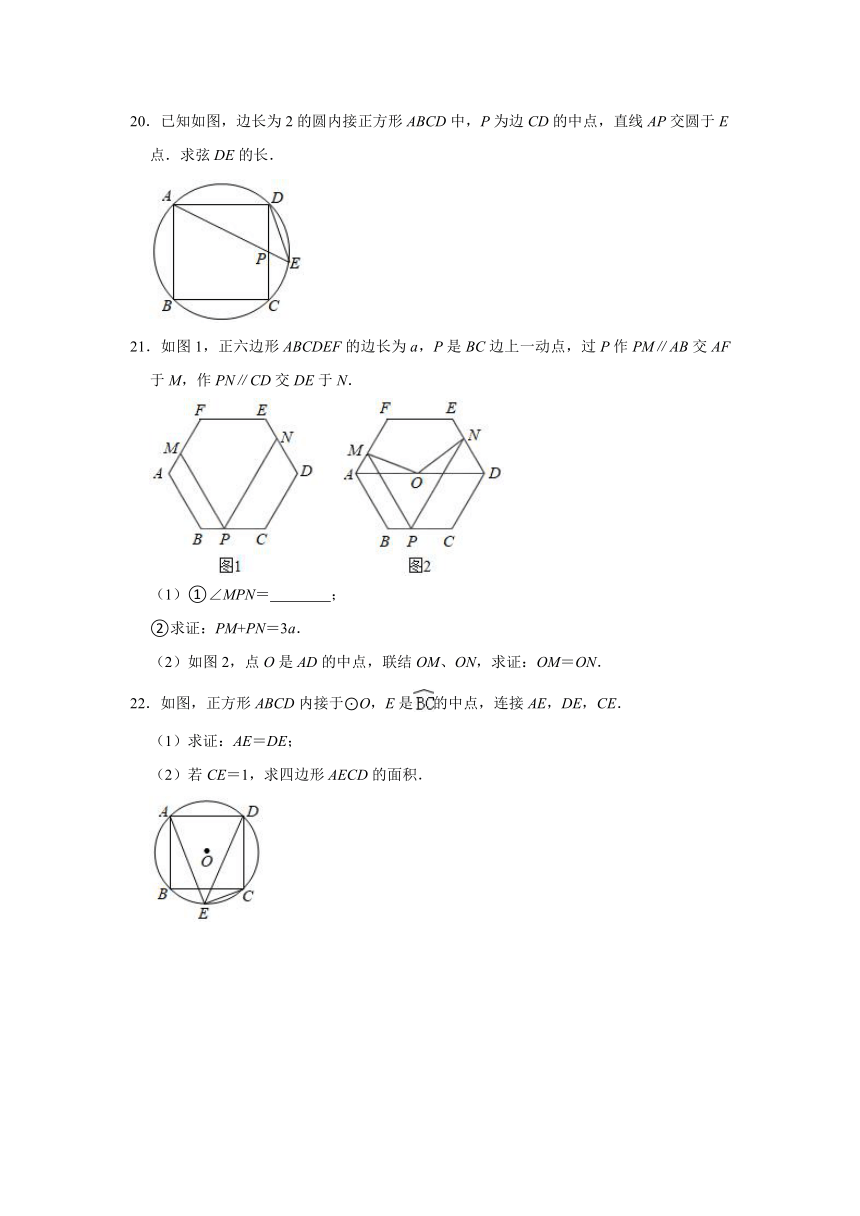
20.已知如图,边长为2的圆内接正方形ABCD中,P为边CD的中点,直线AP交圆于E点.求弦DE的长.
21.如图1,正六边形ABCDEF的边长为a,P是BC边上一动点,过P作PM∥AB交AF于M,作PN∥CD交DE于N.
(1)①∠MPN= ;
②求证:PM+PN=3a.
(2)如图2,点O是AD的中点,联结OM、ON,求证:OM=ON.
22.如图,正方形ABCD内接于⊙O,E是的中点,连接AE,DE,CE.
(1)求证:AE=DE;
(2)若CE=1,求四边形AECD的面积.
参考答案
1.解:如图,连接AC,PC,设AC交EF于点P′,连接BP′.
∵正五边形ABCDE中,点F是BC的中点,
∵EF⊥BC,
∴B,C关于EF对称,
∴PB=PB,
∵PA+PB=PA+PC≥AC,
∴当点P与P′重合时,PA+PB的值最小,
∵ABCDE是正五边形,
∴BA=BC,∠ABC=108°,
∴∠BAC=∠BCA=36°,
∵P′B=CP′,
∴∠P′BC=∠P′CB=36°,
∵∠EFB=90°,
∴∠BP′F=90°﹣∠P′BC=90°﹣36°=54°.
故选:C.
2.解:如图,连接AD,
∵正五边形ABCDE
∴∠DEA==108°,EA=ED,
∴∠DAE=∠DEA=(180°﹣108°)=36°,
故选:A.
3.解:如图,连接OA,OC,
∵ABCDE是正五边形,
∴∠AOC=×2=144°,
∴∠APC=∠AOC=72°,
故选:C.
4.解:连接OA、OB,
∵六边形ABCDEF是⊙O的内接正六边形,
∴∠AOB==60°,
∵OA=OB,
∴△AOB是等边三角形,
∵AB=4,
∴OA=OB=AB=4,
即正六边形ABCDEF的外接圆的半径是4,
故选:B.
5.解:正十边形的中心角为:=36°.
故选:B.
6.解:设O是正六边形的中心,AB是正六边形的一边,OC是边心距,则△OAB是正三角形.
OC=OA sinA=×=,
则S△OAB=AB OC=××=,
则正六边形的面积为6×=3.
故选:C.
7.解:如图所示,连接OE、OF,过O作ON⊥CE于N,
∵多边形ABCDEF是正六边形,
∴∠EOF=60°,
∵OE=OF,
∴△EOF是等边三角形,
∴∠OEM=60°,
∴OM=OE sin∠OEM,
∴OE==,
∵∠OEN=30°,
∴ON=OE=,EN=1.
∴CE=2EN=2.
∴S△ACE=.
故选:D.
8.解:正五边形的内角=(5﹣2)×180°÷5=108°,
∴∠E=∠D=108°,
∵AE、CD分别与⊙O相切于A、C两点,
∴∠OAE=∠OCD=90°,
∴∠AOC=540°﹣90°﹣90°﹣108°﹣108°=144°,
故选:A.
9.解:连接OB、OC,如图,
∵正方形ABCD内接于⊙O,
∴所对的圆心角为90°,
∴∠BOC=90°,
∴∠BPC=∠BOC=45°.
故选:B.
10.解:⊙O的面积为2π,则圆的半径为,则BD=2=AC,
由正方形的性质,知点C是点A关于BD的对称点,
过点C作CA′∥BD,且使CA′=1,
连接AA′交BD于点N,取NM=1,连接AM、CM,则点M、N为所求点,
理由:∵A′C∥MN,且A′C=MN,则四边形MCA′N为平行四边形,
则A′N=CM=AM,
故△AMN的周长=AM+AN+MN=AA′+1为最小,
则A′A==3,
则△AMN的周长的最小值为3+1=4,
故选:B.
11.解:连接OC,OD.
在正五边形ABCDE中,∠COD==72°,
∴∠CPD=∠COD=36°,
∵DG⊥PC,
∴∠PGD=90°,
∴∠PDG=90°﹣36°=54°,
故选:B.
12.解:连接OA,OB,如图所示:
∵六边形ABCDEF是正六边形,
∴∠AOB==60°,
当点P不在上时,
∠APB=∠AOB=30°,
当点P在上时,
∠APB=180°﹣∠AOB=180°﹣30°=150°,
故选:A.
13.解:连接OA,OB,OE,
∵正方形ABCD内接于⊙O,
∴OA=OB=OE,∠AOB==90°,AB=BC,∠ABC=90°,
∴∠OAB=∠OBA=(180°﹣∠AOB)=45°,
∴∠OBC=∠ABC﹣∠OBA=45°,
∵∠CBE=15°,
∴∠OBE=∠OBC+∠CBE=60°,
∴△OBE是等边三角形,
∴OB=BE=3,
∴OA=3,
∴AB==3,
∴BC=3,
故选:D.
14.解:在正六边形ABCDEF中,BC=CD=DE=4,∠BCD=∠CDE=120°,
∴∠DCE=∠DEC=30°,
∵AD⊥CE,
∴OC=OE=CD cos30°=2,
∵∠BCO=∠BCD﹣∠DCO=90°,
∴OB===2,
故答案为:2.
15.解:在正六边形ABCDEF中,∠BCD=120°,
∵CB=CD,
∴∠CBD=∠CDB=(180°﹣120°)=30°,
故答案为:30°.
16.解:连接OB交AC于M,
∵正八边形ABCDEFGH内接于⊙O,
∴∠AOB=∠BOC==45°,AB=BC,
∴=,∠AOC=90°,
∴AM=CM=AC=2,OM⊥AC,
∵OA=OC,
∠OAM=∠OCA=(180°﹣∠AOC)=45°,
∴∠OAM=∠AOB,
∴AM=OM,
在Rt△AOC中,
∵OA=OC,OA2+OC2=AC2,
∴2OA2=AC2=42=16,
∴OA=2,
在Rt△AOM中,
∵OM2+AM2=OA2,
∴2OM2=(2)2,
∴OM=2,
∴点O到AC距离为2,
故答案为:2.
17.解:∵AF是⊙O的直径,五边形ABCDE是⊙O的内接正五边形,
∴=,=∠BAE=108°,
∴=,
∴∠BAF=∠BAE=54°,
∴∠BDF=∠BAF=54°.
18.解:如图所示,连接OC、OB,过O作ON⊥CE于N,
∵多边形ABCDEF是正六边形,
∴∠COB=60°,
∵OC=OB,
∴△COB是等边三角形,
∴∠OCM=60°,
∴OM=OC sin∠OCM,
∴OC==.
∵∠OCN=30°,
∴ON=OC=,CN=2,
∴CE=2CN=4,
∴该圆的内接正三角形ACE的面积=3××4×=4.
19.解:(1)∵五边形ABCDE是正五边形,
∴AB=BC=CD=DE=EA,∠ABC==108°,
∴∠BAC=∠ACB==36°;
(2)由(1)可得∠ABE=∠AEB=36°,
∴∠CBF=∠ABC﹣∠ABE=108°﹣36°=72°,
在△BCF中,∠BFC=180°﹣72°﹣36°=72°,
∴BC=CF,
同理可得AE=EF,
∴CD=DE=EF=FC,
∴四边形CDEF为菱形.
20.解:连接CE,作EF⊥PF
∵∠DAP=∠PCE,∠APD=∠CPE,
∴△APD∽△CPE,
∴=,
∵P为边CD的中点,
∴DP=PC=1,
∴AP===,
∴=,
∴PE=,
∵FE∥AD
∴△APD∽△EPF,
∴=,
∴=,
∴PF=,
∴EF=,
∴DE==.
21.解:(1)①∵六边形ABCDEF是正六边形,
∴∠A=∠B=∠C=∠D=∠E=∠F=120°
又∴PM∥AB,PN∥CD,
∴∠BPM=60°,∠NPC=60°,
∴∠MPN=180°﹣∠BPM﹣∠NPC=180°﹣60°﹣60°=60°,
故答案为:60°.
②如图1,作AG⊥MP交MP于点G,BH⊥MP于点H,CL⊥PN于点L,DK⊥PN于点K,
MP+PN=MG+GH+HP+PL+LK+KN,
∵正六边形ABCDEF中,PM∥AB,PN∥CD,
∴∠AMG=∠BPH=∠CPL=∠DNK=60°,
∴GM=AM,HP=BP,PL=PC,NK=ND,
∵AM=BP,PC=DN,
∴MG+HP+PL+KN=a,GH=LK=a,
∴MP+PN=MG+GH+HP+PL+LK+KN=3a.
(2)如图2,连接OE,
∵六边形ABCDEF是正六边形,AB∥MP,PN∥DC,
∴AM=BP=EN,
∵∠MAO=∠OEN=60°,OA=OE,
在△ONE和△OMA中,
,
∴△OMA≌△ONE(SAS),
∴OM=ON.
22.(1)证明:∵四边形ABCD是正方形,
∴AB=CD,
∴=,
∵E是的中点,
∴=,
∴+=+,即=,
∴AE=DE.
(2)解:连接BD,AO,过点D作DF⊥DE交EC的延长线于F.
∵四边形ABCD是正方形,
∴∠DBC=∠DEC=45°,DA=DC,
∵∠EDF=90°,
∴∠F=∠EDF﹣∠DEF=90°﹣45°=45°,
∴DE=DF,
∵∠AED=∠AOD=45°,
∴∠AED=∠F=45°,
∵∠ADC=∠EDF=90°,
∴∠ADE+∠EDC=∠CDF+∠EDC=90°,
∴∠ADE=∠CDF
在△ADE和△CDF中,
,
∴△ADE≌△CDF(AAS),
∴AE=CF,
∴S△ADE=S△CDF,
∴S四边形AECD=S△DEF,
∵EF=DE=EC+DE,EC=1,
∴1+DE=DE,
∴DE=+1,
∴S四边形AECD=S△DEF=DE2=+.
1.如图,已知正五边形ABCDE中,点F是BC的中点,P是线段EF上的动点,连接AP,BP,当AP+BP的值最小时,∠BPF的度数为( )
A.36° B.45° C.54° D.60°
2.如图,正五边形ABCDE内接于⊙O,则∠DAE的度数是( )
A.36° B.26° C.30° D.45°
3.如图,⊙O是正五边形ABCDE的外接圆,点P为上的一点,则∠APC的度数为( )
A.36° B.60° C.72° D.75°
4.若正六边形的边长为4,则它的外接圆的半径为( )
A.4 B.4 C.2 D.2
5.正十边形的中心角是( )
A.18° B.36° C.72° D.144°
6.已知正六边形的半径为,则此正六边形的面积为( )
A. B.2 C.3 D.4
7.如图,已知⊙O的内接正六边形ABCDEF的边心距OM=1,则该圆的内接正三角形ACE的面积为( )
A.2 B.4 C. D.
8.如图,⊙O与正五边形ABCDE的两边AE,CD相切于A,C两点,则∠AOC的度数是( )
A.144° B.130° C.129° D.108°
9.如图,正方形ABCD内接于⊙O,点P在上,则∠BPC的度数为( )
A.30° B.45° C.60° D.90°
10.如图,正方形ABCD内接于⊙O,线段MN在对角线BD上运动,若⊙O的面积为2π,MN=1,则△AMN周长的最小值是( )
A.3 B.4 C.5 D.6
11.如图,正五边形ABCDE内接于⊙O,点P为上一点(点P与点D,点E不重合),连接PC,PD,DG⊥PC,垂足为G,则∠PDG等于( )
A.72° B.54° C.36° D.64°
12.如图,⊙O是正六边形ABCDEF的外接圆,点P在⊙O上(P不与A,B重合),则∠APB的度数为( )
A.30°或150° B.60°或120° C.30° D.60°
13.如图,正方形ABCD内接于⊙O.点E为上一点,连接BE、CE,若∠CBE=15°,BE=3,则BC的长为( )
A. B. C. D.
14.如图,在正六边形ABCDEF中,连接CE,AD,AD与CE交于点O,连接OB,若正六边形边长为4,则OB的长为 .
15.如图,正六边形ABCDEF内接于⊙O,连接BD,则∠CBD的度数是 .
16.如图,正八边形ABCDEFGH内接于⊙O,若AC=4,则点O到AC的距离为 .
17.如图,五边形ABCDE是⊙O的内接正五边形,AF是⊙O的直径,求∠BDF的度数.
18.如图,已知⊙O的内接正六边形ABCDEF的边心距OM=2,求该圆的内接正三角形ACE的面积.
19.如图,⊙O的内接正五边形ABCDE中,对角线AC和BE相交于点F.
(1)求∠BAC的度数.
(2)求证:四边形CDEF为菱形.
20.已知如图,边长为2的圆内接正方形ABCD中,P为边CD的中点,直线AP交圆于E点.求弦DE的长.
21.如图1,正六边形ABCDEF的边长为a,P是BC边上一动点,过P作PM∥AB交AF于M,作PN∥CD交DE于N.
(1)①∠MPN= ;
②求证:PM+PN=3a.
(2)如图2,点O是AD的中点,联结OM、ON,求证:OM=ON.
22.如图,正方形ABCD内接于⊙O,E是的中点,连接AE,DE,CE.
(1)求证:AE=DE;
(2)若CE=1,求四边形AECD的面积.
参考答案
1.解:如图,连接AC,PC,设AC交EF于点P′,连接BP′.
∵正五边形ABCDE中,点F是BC的中点,
∵EF⊥BC,
∴B,C关于EF对称,
∴PB=PB,
∵PA+PB=PA+PC≥AC,
∴当点P与P′重合时,PA+PB的值最小,
∵ABCDE是正五边形,
∴BA=BC,∠ABC=108°,
∴∠BAC=∠BCA=36°,
∵P′B=CP′,
∴∠P′BC=∠P′CB=36°,
∵∠EFB=90°,
∴∠BP′F=90°﹣∠P′BC=90°﹣36°=54°.
故选:C.
2.解:如图,连接AD,
∵正五边形ABCDE
∴∠DEA==108°,EA=ED,
∴∠DAE=∠DEA=(180°﹣108°)=36°,
故选:A.
3.解:如图,连接OA,OC,
∵ABCDE是正五边形,
∴∠AOC=×2=144°,
∴∠APC=∠AOC=72°,
故选:C.
4.解:连接OA、OB,
∵六边形ABCDEF是⊙O的内接正六边形,
∴∠AOB==60°,
∵OA=OB,
∴△AOB是等边三角形,
∵AB=4,
∴OA=OB=AB=4,
即正六边形ABCDEF的外接圆的半径是4,
故选:B.
5.解:正十边形的中心角为:=36°.
故选:B.
6.解:设O是正六边形的中心,AB是正六边形的一边,OC是边心距,则△OAB是正三角形.
OC=OA sinA=×=,
则S△OAB=AB OC=××=,
则正六边形的面积为6×=3.
故选:C.
7.解:如图所示,连接OE、OF,过O作ON⊥CE于N,
∵多边形ABCDEF是正六边形,
∴∠EOF=60°,
∵OE=OF,
∴△EOF是等边三角形,
∴∠OEM=60°,
∴OM=OE sin∠OEM,
∴OE==,
∵∠OEN=30°,
∴ON=OE=,EN=1.
∴CE=2EN=2.
∴S△ACE=.
故选:D.
8.解:正五边形的内角=(5﹣2)×180°÷5=108°,
∴∠E=∠D=108°,
∵AE、CD分别与⊙O相切于A、C两点,
∴∠OAE=∠OCD=90°,
∴∠AOC=540°﹣90°﹣90°﹣108°﹣108°=144°,
故选:A.
9.解:连接OB、OC,如图,
∵正方形ABCD内接于⊙O,
∴所对的圆心角为90°,
∴∠BOC=90°,
∴∠BPC=∠BOC=45°.
故选:B.
10.解:⊙O的面积为2π,则圆的半径为,则BD=2=AC,
由正方形的性质,知点C是点A关于BD的对称点,
过点C作CA′∥BD,且使CA′=1,
连接AA′交BD于点N,取NM=1,连接AM、CM,则点M、N为所求点,
理由:∵A′C∥MN,且A′C=MN,则四边形MCA′N为平行四边形,
则A′N=CM=AM,
故△AMN的周长=AM+AN+MN=AA′+1为最小,
则A′A==3,
则△AMN的周长的最小值为3+1=4,
故选:B.
11.解:连接OC,OD.
在正五边形ABCDE中,∠COD==72°,
∴∠CPD=∠COD=36°,
∵DG⊥PC,
∴∠PGD=90°,
∴∠PDG=90°﹣36°=54°,
故选:B.
12.解:连接OA,OB,如图所示:
∵六边形ABCDEF是正六边形,
∴∠AOB==60°,
当点P不在上时,
∠APB=∠AOB=30°,
当点P在上时,
∠APB=180°﹣∠AOB=180°﹣30°=150°,
故选:A.
13.解:连接OA,OB,OE,
∵正方形ABCD内接于⊙O,
∴OA=OB=OE,∠AOB==90°,AB=BC,∠ABC=90°,
∴∠OAB=∠OBA=(180°﹣∠AOB)=45°,
∴∠OBC=∠ABC﹣∠OBA=45°,
∵∠CBE=15°,
∴∠OBE=∠OBC+∠CBE=60°,
∴△OBE是等边三角形,
∴OB=BE=3,
∴OA=3,
∴AB==3,
∴BC=3,
故选:D.
14.解:在正六边形ABCDEF中,BC=CD=DE=4,∠BCD=∠CDE=120°,
∴∠DCE=∠DEC=30°,
∵AD⊥CE,
∴OC=OE=CD cos30°=2,
∵∠BCO=∠BCD﹣∠DCO=90°,
∴OB===2,
故答案为:2.
15.解:在正六边形ABCDEF中,∠BCD=120°,
∵CB=CD,
∴∠CBD=∠CDB=(180°﹣120°)=30°,
故答案为:30°.
16.解:连接OB交AC于M,
∵正八边形ABCDEFGH内接于⊙O,
∴∠AOB=∠BOC==45°,AB=BC,
∴=,∠AOC=90°,
∴AM=CM=AC=2,OM⊥AC,
∵OA=OC,
∠OAM=∠OCA=(180°﹣∠AOC)=45°,
∴∠OAM=∠AOB,
∴AM=OM,
在Rt△AOC中,
∵OA=OC,OA2+OC2=AC2,
∴2OA2=AC2=42=16,
∴OA=2,
在Rt△AOM中,
∵OM2+AM2=OA2,
∴2OM2=(2)2,
∴OM=2,
∴点O到AC距离为2,
故答案为:2.
17.解:∵AF是⊙O的直径,五边形ABCDE是⊙O的内接正五边形,
∴=,=∠BAE=108°,
∴=,
∴∠BAF=∠BAE=54°,
∴∠BDF=∠BAF=54°.
18.解:如图所示,连接OC、OB,过O作ON⊥CE于N,
∵多边形ABCDEF是正六边形,
∴∠COB=60°,
∵OC=OB,
∴△COB是等边三角形,
∴∠OCM=60°,
∴OM=OC sin∠OCM,
∴OC==.
∵∠OCN=30°,
∴ON=OC=,CN=2,
∴CE=2CN=4,
∴该圆的内接正三角形ACE的面积=3××4×=4.
19.解:(1)∵五边形ABCDE是正五边形,
∴AB=BC=CD=DE=EA,∠ABC==108°,
∴∠BAC=∠ACB==36°;
(2)由(1)可得∠ABE=∠AEB=36°,
∴∠CBF=∠ABC﹣∠ABE=108°﹣36°=72°,
在△BCF中,∠BFC=180°﹣72°﹣36°=72°,
∴BC=CF,
同理可得AE=EF,
∴CD=DE=EF=FC,
∴四边形CDEF为菱形.
20.解:连接CE,作EF⊥PF
∵∠DAP=∠PCE,∠APD=∠CPE,
∴△APD∽△CPE,
∴=,
∵P为边CD的中点,
∴DP=PC=1,
∴AP===,
∴=,
∴PE=,
∵FE∥AD
∴△APD∽△EPF,
∴=,
∴=,
∴PF=,
∴EF=,
∴DE==.
21.解:(1)①∵六边形ABCDEF是正六边形,
∴∠A=∠B=∠C=∠D=∠E=∠F=120°
又∴PM∥AB,PN∥CD,
∴∠BPM=60°,∠NPC=60°,
∴∠MPN=180°﹣∠BPM﹣∠NPC=180°﹣60°﹣60°=60°,
故答案为:60°.
②如图1,作AG⊥MP交MP于点G,BH⊥MP于点H,CL⊥PN于点L,DK⊥PN于点K,
MP+PN=MG+GH+HP+PL+LK+KN,
∵正六边形ABCDEF中,PM∥AB,PN∥CD,
∴∠AMG=∠BPH=∠CPL=∠DNK=60°,
∴GM=AM,HP=BP,PL=PC,NK=ND,
∵AM=BP,PC=DN,
∴MG+HP+PL+KN=a,GH=LK=a,
∴MP+PN=MG+GH+HP+PL+LK+KN=3a.
(2)如图2,连接OE,
∵六边形ABCDEF是正六边形,AB∥MP,PN∥DC,
∴AM=BP=EN,
∵∠MAO=∠OEN=60°,OA=OE,
在△ONE和△OMA中,
,
∴△OMA≌△ONE(SAS),
∴OM=ON.
22.(1)证明:∵四边形ABCD是正方形,
∴AB=CD,
∴=,
∵E是的中点,
∴=,
∴+=+,即=,
∴AE=DE.
(2)解:连接BD,AO,过点D作DF⊥DE交EC的延长线于F.
∵四边形ABCD是正方形,
∴∠DBC=∠DEC=45°,DA=DC,
∵∠EDF=90°,
∴∠F=∠EDF﹣∠DEF=90°﹣45°=45°,
∴DE=DF,
∵∠AED=∠AOD=45°,
∴∠AED=∠F=45°,
∵∠ADC=∠EDF=90°,
∴∠ADE+∠EDC=∠CDF+∠EDC=90°,
∴∠ADE=∠CDF
在△ADE和△CDF中,
,
∴△ADE≌△CDF(AAS),
∴AE=CF,
∴S△ADE=S△CDF,
∴S四边形AECD=S△DEF,
∵EF=DE=EC+DE,EC=1,
∴1+DE=DE,
∴DE=+1,
∴S四边形AECD=S△DEF=DE2=+.
