2021-2022学年苏科版数学九年级下册5.3用待定系数法确定二次函数表达式基础练习(Word版含解析)
文档属性
| 名称 | 2021-2022学年苏科版数学九年级下册5.3用待定系数法确定二次函数表达式基础练习(Word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 133.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-04 20:39:26 | ||
图片预览



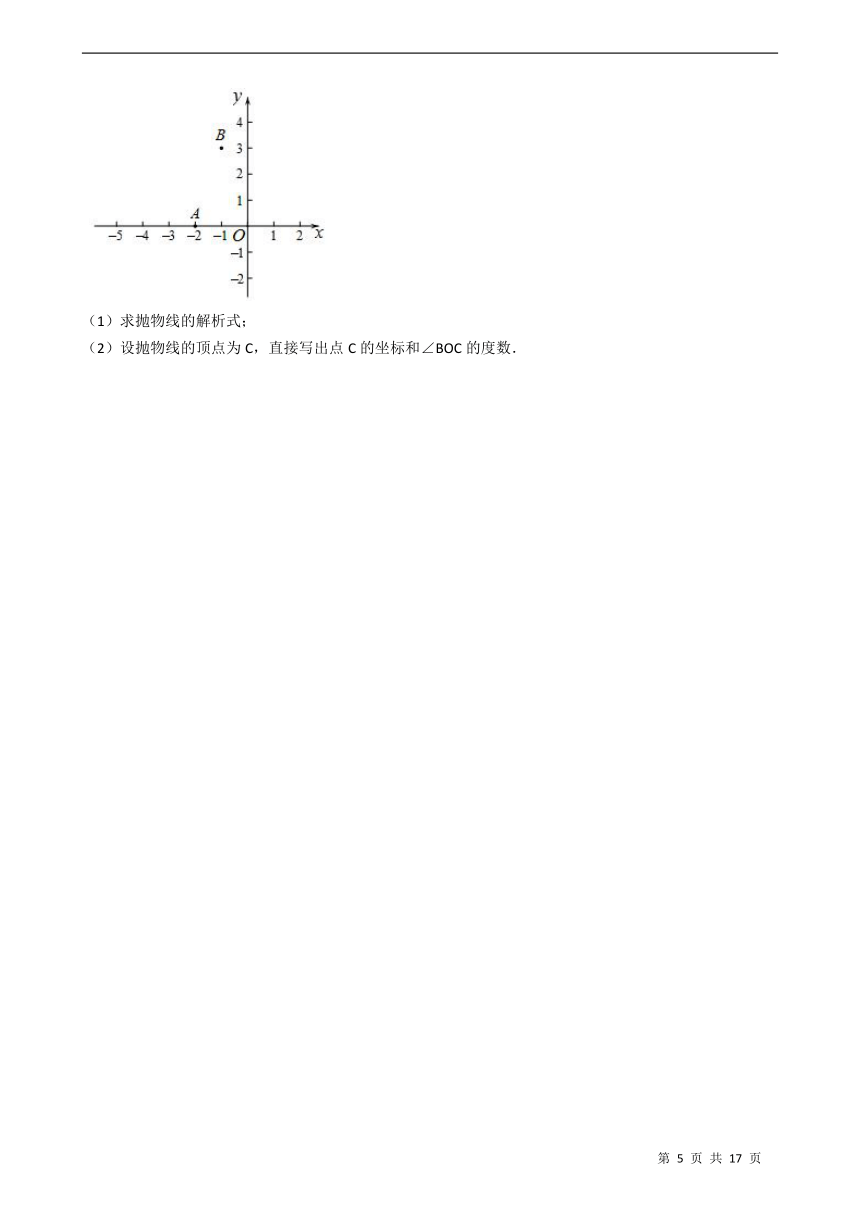
文档简介
5.3用待定系数法确定二次函数表达式基础练习
一、单选题
1.若二次函数y=ax2的图象经过点p(-2 , 4),则该图象必经过点( )
A. (2, 4) B. (-2, - 4) C. (- 4, 2) D. (4, -2)
2.二次函数的图象如图所示,则这个二次函数的解析式为( )
A. y= (x﹣2)2+3 B. y= (x﹣2)2﹣3
C. y=﹣ (x﹣2)2+3 D. y=﹣ (x﹣2)2﹣3
3.已知二次函数的图象如图所示,则这个二次函数的表达式为( )
A. B. C. D.
4.如图,是一条抛物线的图象,则其解析式为( )
A. y=x2﹣2x+3 B. y=x2﹣2x﹣3 C. y=x2+2x+3 D. y=x2+2x-3
5.若二次函数y=ax2+bx+c的x与y对应值如下表:则当x=1时,y的值为( ).
A. 5 B. -3 C. -13 D. -27
6.已知二次函数y=ax2+bx+c的图象上部分点的横坐标x与纵坐标y的对应值如下表:
x … -1 0 1 2 …
y … 0 3 4 3 …
那么关于它的图象,下列判断正确的是( )
A. 开口向上 B. 与x轴的另一个交点是(3,0)
C. 与y轴交于负半轴 D. 在直线x=1的左侧部分是下降的
7.已知点A(1,1) 、B(3,1) 、C(4,2) 、D(2,2), 若抛物线y=ax2(a>0)与四边形ABCD的边没有交点,则a的取值范围为( )
A. < a< 1 B. < a< 1 C. a>l或0< a< D. a>1或08.图(1)是一个横断面为抛物线形状的拱桥,当水面在图(1)位置时,拱顶(拱桥洞的最高点)离水面2m,水面宽4m.如图(2)建立平面直角坐标系,则抛物线的关系式是( )
A. y=-2 B. y=2 C. y= - D. y=
9.某同学在用描点法画二次函数y=ax2+bx+c的图象时,列出了下面的表格:由于粗心,他算错了其中一个y值,则这个错误的数值是( )
A. ﹣11 B. ﹣2 C. 1 D. ﹣5
10.如图, 在平面直角坐标系中, 矩形O ABC的点B坐标为(8, 6) ,点A在x轴上,点C在y轴上.点D是边AB上的动点,连接OD,作点A关于线段OD的对称点A'.已知一条抛物线y=ax +bx+c(a≠0)经过O,A',A三点,且点A'恰好是抛物线的顶点,则b的值为( )
A. - B. 2 C. -2 D.
二、填空题
11.若一个二次函数的二次项系数为-1,且图象的顶点坐标为(0,-3).则这个二次函数的表达式为 .
12.请写出一个对称轴为x=1的抛物线的解析式________.
13.已知二次函数y=ax2的图象经过点A(-2, ).则该函数的解析式为________.
14.抛物线 过点A(2,3),则此抛物线开口向________.
15.一条抛物线的顶点是A(2,1),且经过点B(1,0),则该抛物线的函数表达式是 .
16.抛物线y=2x2+3x+k﹣2经过点(﹣1,0),那么k= .
17.若二次函数 的图象经过点(-1,0),(1,-2),当 随 的增大而增大时, 的取值范围是 。
18.二次函数 为常数, 中的 与 的部分对应值如下表:
x -1 0 3
y n -3 -3
当 时,下列结论中一定正确的是 (填序号即可)
① ;②当 时, 的值随 值的增大而增大;③ ;④当 时,关于 的一元二次方程 的解是 , .
三、解答题
19.如图,已知点A(-4,8)和点B(2,n)在抛物线y=ax2上.求a的值及点B的坐标.
20.已知抛物线的顶点是 A(2,﹣3),且交 y 轴于点 B(0,5),求此抛物线的解析式.
21.已知二次函数的图象与x轴交于点(-1,0)和 (3,0),并且与y轴交于点(0,3).求这个二次函数表达式.
22.二次函数y=ax2+bx+c(a≠0)的图象过点A(﹣1,8)、B(2,﹣1),与y轴交于点C(0,3),求二次函数的表达式.
23.已知抛物线的顶点坐标 且过点 ,求该抛物线的解析式.
24.二次函数y= (x+h)2的图象如图所示,已知OA=OC,试求该抛物线的解析式.
25.已知一个二次函数图象上部分点的横坐标x与纵坐标y的对应值如表所示:
x …… ﹣3 ﹣2 ﹣1 0 1 ……
y …… 0 ﹣3 ﹣4 ﹣3 0 ……
求这个二次函数的表达式.
26.如图,直线y=x+3与坐标轴分别交于A,B两点,抛物线y=ax2+bx-3a经过点A,B,顶点为C,连接CB并延长交x轴于点E,点D与点B关于抛物线的对称轴MN对称.
(1)求抛物线的解析式及顶点C的坐标;
(2)求证:四边形ABCD是直角梯形.
27.如图,在平面直角坐标系中,二次函数y=+bx+c的图象与x轴交于A、B两点, A点在原点的左侧,B点的坐标为(3,0),与y轴交于C(0,-3)点,点P是直线BC下方的抛物线上一动点.
(1)求这个二次函数的表达式.
(2)连结PO、PC,并把△POC沿CO翻折,得到四边形POP’C,那么是否存在点P,使四边形POP’C为菱形?若存在,请求出此时点P的坐标;若不存在,请说明理由.
(3)当点P运动到什么位置时,四边形 ABPC的面积最大并求出此时P点的坐标和四边形ABPC的最大面积.
28.如图,在平面直角坐标系xOy中,抛物线y=x2+ax+b经过点A(-2,0),B(-1,3).
(1)求抛物线的解析式;
(2)设抛物线的顶点为C,直接写出点C的坐标和∠BOC的度数.
答案解析部分
一、单选题
1.【答案】 B
【考点】待定系数法求二次函数解析式
【解析】【解答】解:AC、由题意得:-4=a(-2)2, 解得a=-1, ∴y=-x2, ∴y≤0,AC不符合题意;
BD、当x=-2时,y=-x2=-4, 当x=4时,y=-16,∴ B符合题意,D不符合题意;
故答案为:B.
【分析】先把P代入函数,求出a值,得y=-x2≤0,排除不符合项,再代入点的坐标即可确定图象必过之点.
2.【答案】 C
【考点】待定系数法求二次函数解析式
【解析】【解答】解:抛物线开口向下,顶点是(2,3),所以y=﹣ (x﹣2)2+3,
故答案为:C.
【分析】根据二次函数的开口方向向下和顶点坐标即可判断。
3.【答案】 B
【考点】待定系数法求二次函数解析式
【解析】【解答】根据题意,图象与y轴交于负半轴,故c为负数,又四个选项中,B、C的c为-3,符合题意,故设二次函数的表达式为y=ax2+bx+c,
抛物线过(-1,0),(0,-3),(3,0),
所以
解得a=1,b=-2,c=-3,
这个二次函数的表达式为y=x2-2x-3.
故答案为:B.
【分析】根据题意,把抛物线经过的三点代入函数的表达式,列出方程组,解出各系数则可
4.【答案】 B
【考点】待定系数法求二次函数解析式
【解析】【解答】解:因为抛物线与x轴的交点坐标为(-1,0),(3,0),
可设交点式为y=a(x+1)(x-3),
把(0,-3)代入y=a(x+1)(x-3),
可得:-3=a(0+1)(0-3),
解得:a=1,
所以解析式为:y=x2-2x-3,
故答案为:B.
【分析】观察图象可知抛物线与x轴和y轴的两个交点坐标,于是可将抛物线的解析式设为交点式,再把抛物线与y轴的交点坐标代入解析式计算即可求解.
5.【答案】 C
【考点】待定系数法求二次函数解析式
【解析】
【分析】由表可知,抛物线的对称轴为直线x=-3,顶点坐标为(-3,5),再用待定系数法求得二次函数的解析式,再把x=0代入即可求得y的值.
【解答】设二次函数的解析式为y=a(x-h)2+k,
∵当x=-4或-2时,y=3,由抛物线的对称性可知h=-3,k=5,
∴y=a(x+3)2+5,
把(-2,3)代入得,a=-2,
∴二次函数的解析式为y=-2(x+3)2+5,
当x=0时,y=-13.
故选C.
6.【答案】 B
【考点】待定系数法求二次函数解析式,二次函数y=ax^2+bx+c的性质
【解析】【解答】A、由表格知,抛物线的顶点坐标是(1,4).故设抛物线解析式为y=a(x﹣1)2+4.
将(﹣1,0)代入,得
a(﹣1﹣1)2+4=0,
解得a=﹣2.
∵a=﹣2<0,
∴抛物线的开口方向向下,
故本选项不符合题意;
B、抛物线与x轴的一个交点为(﹣1,0),对称轴是x=1,则抛物线与x轴的另一个交点是(3,0),故本选项符合题意;
C、由表格知,抛物线与y轴的交点坐标是(0,3),即与y轴交于正半轴,故本选项不符合题意;
D、抛物线开口方向向下,对称轴为x=1,则在直线x=1的左侧部分是上升的,故本选项不符合题意;
故答案为:B.
【分析】(1)由表格中的信息可知,抛物线的顶点坐标是(1,4),所以设抛物线解析式为y=a(x﹣1)2+4;将(﹣1,0)代入,解得a=﹣2,而﹣2<0,所以抛物线的开口方向向下;
(2)由(1)知,对称轴是x=1,所以根据已知点抛物线与x轴的一个交点为(﹣1,0)可得抛物线与x轴的另一个交点是(3,0);
(3)由表格中的信息可知,抛物线与y轴的交点坐标是(0,3),即与y轴交于正半轴;
(4)由(1)知,抛物线开口方向向下,对称轴为x=1,则在直线x=1的左侧部分是上升的。
7.【答案】 D
【考点】待定系数法求二次函数解析式,二次函数y=ax^2+bx+c的图象
【解析】【解答】解:如图所示:把A(1,1)代入y=ax2得,a=1,
把B(3,1)代入y=ax2得a= ,
∵抛物线的开口越小,|a|的绝对值越大,
∴抛物y=ax2与四边形ABCD的边没有交点,则a的取值范围为:a>1或0故答案为:D.
【分析】先求出a= ,再根据抛物线的开口越小,|a|的绝对值越大,求解即可。
8.【答案】 C
【考点】待定系数法求二次函数解析式
【解析】【解答】抛物线顶点为(0,0),所以设抛物线方程为 (2,-2)是图像上的点,所以
故答案为:C
【分析】根据抛物线的顶点是原点,对称轴是1由轴,解析式可设为由题意知,点(2,-2)在抛物线上,利用待定系数法求出解析式即可。
9.【答案】 D
【考点】待定系数法求二次函数解析式
【解析】【解答】解:由已知数据可得函数图象关于y轴对称,则不符合题意应出现在x=-2或x=2时,
故函数的顶点坐标为(0,1),
,
当x=1时, 解得 ,
当 时, ,
∴错误的数值是-5,
故答案为:D。
【分析】由已知可得函数图像关于y轴对称,则不符合题意应该出现在x=-2或x=2时,根据正确的数据求出函数的解析式,进而可得答案。
10.【答案】 B
【考点】坐标与图形性质,待定系数法求二次函数解析式,矩形的性质,轴对称的性质,二次函数图象上点的坐标特征
【解析】【解答】如图,过点A'作A'E⊥OA于E,连接A'O,A'A,
∵ 矩形O ABC的点B坐标为(8, 6) ,∴OA=8,
∵ 点A关于线段OD的对称点A',∴A'O=OA,
∵抛物线y=ax +bx+c(a≠0)经过O,A',A三点,且点A'恰好是抛物线的顶点,
∴A'O=A'A,∴A'O=A'A=OA,∴△A'AO是等边三角形,
∴A'O=A'A=OA=8,
∵A'E⊥OA,∴OE=AO=4,
∴A'A==4 , ∴A'(4,4),
∵ 点A'是抛物线的顶点,
∴设 y=a(x-4) +4,
将点O(0,0)代入解析式中,得a=,
∴y=(x-4) +4=x2+2x,
∴b=2.
【分析】如图,过点A'作A'E⊥OA于E,连接A'O,A'A,根据矩形及轴对称的性质,可得A'O=OA=8,利用抛物线y=ax +bx+c(a≠0)经过O,A',A三点,且点A'恰好是抛物线的顶点,可得△A'AO是等边三角形,从而可得OE=AO=4,利用勾股定理求出A'A==4 , 可得A'(4,4),从而可得设y=a(x-4) +4,将点O(0,0)代入解析式中求出a值,可得y=(x-4) +4=x2+2x,据此即可求出结论.
二、填空题
11.【答案】 y=﹣x2﹣3
【考点】待定系数法求二次函数解析式
【解析】【解答】解:∵抛物线二次项系数为-1,顶点坐标为(0,-3),
∴抛物线的顶点式为y=-(x-0)2-3,即y=-x2-3;
故答案是y=-x2-3。
【分析】把抛物线设为顶点式,化为一般式即可.
12.【答案】 y=(x﹣1)2
【考点】待定系数法求二次函数解析式
【解析】【解答】解:抛物线y=(x﹣1)2的对称轴为直线x=1.
故答案为:y=(x﹣1)2 .
【分析】利用二次函数的性质写出一个顶点的横坐标为1的抛物线解析式即可.
13.【答案】
【考点】待定系数法求二次函数解析式
【解析】【解答】解:将点A(-2,- )代入y=ax2得a= ,
∴该函数的解析式为 ,
故答案为 : .
【分析】将点A(-2,- )代入y=ax2即可得到a的值.
14.【答案】 上
【考点】待定系数法求二次函数解析式,二次函数y=ax^2+bx+c的性质
【解析】【解答】解:∵抛物线 过点A(2,3),
∴4a-8+3=3
∴a=2>0
∴此抛物线开口向上
故答案为:上
【分析】将点A的坐标代入抛物线的解析式可得4a-8+3=3,求出a的值再判断开口方向即可。
15.【答案】 (或 )
【考点】待定系数法求二次函数解析式
【解析】【解答】设抛物线解析式为y=a(x-2)2+1,
把B(1,0)代入得a+1=0,解得a=-1,
所以抛物线解析式为y=-(x-2)2+1,即y=-x2+4x-3
故答案为: (或y=-x2+4x-3).
【分析】已知抛物线的顶点坐标,因此设函数解析式为顶点式,再将点B的坐标代入计算,即可得出函数解析式。
16.【答案】 3
【考点】待定系数法求二次函数解析式
【解析】【解答】∵抛物线y=2x2+3x+k-2经过点(-1,0),
∴0=2-3+k-2,
解得k=3.
故答案为:3.
【分析】将已知点的坐标代入函数解析式,建立关于k的方程,求解即可。
17.【答案】 x>
【考点】待定系数法求二次函数解析式,二次函数y=ax^2+bx+c的性质,二次函数y=ax^2+bx+c与二次函数y=a(x-h)^2+k的转化
【解析】【解答】将(-1,0),(1,-2)代入函数解析式得 解得
则函数解析式为y=x2-x-2=(x- )2- ,
根据抛物线性质可知当x> 时,函数值y随x的增大而增大.
故答案为:x>
【分析】分别将(-1,0),(1,-2)代入函数解析式,得出关于B,C的二元一次方程组,求解得出b,c的值,从而求出抛物线的解析式,再将解析式配成顶点式,由于此函数的二次项系数大于0,图像开口向上,顶点右侧y随x的增大而增大,从而得出答案。
18.【答案】 ①②④
【考点】待定系数法求二次函数解析式,二次函数y=ax^2+bx+c的图象,二次函数y=ax^2+bx+c的性质
【解析】【解答】解:由表格数据知,二次函数的对称轴为 ,且c=-3<0,
∵n>0,∴a>0,
∵对称轴 >0,
∴b<0即 bc>0,故①正确;
∵a>0,对称轴为 ,
∴当x> 时, 的值随 值的增大而增大,
∴当 时, 的值随 值的增大而增大,
故②正确;
③由对称轴 得:b=-3a,
∴
∵当x=-1时,y=n,
∴n=a+3a-3=4a-3,
∴n﹤4a,故③错误;
④当n=1时,将(-1,1),(0,-3),(3,-3)代入函数解析式中,得:
,
解得 ,
∴关于x的一元二次方程为 ,解得 , ,
故④正确,
故答案为:①②④.
【分析】①根据表格数据得到对称轴为 ,c=-3<0,又n>0知a>0,即可得出答案;②根据二次函数的性质即可解答;③根据二次函数的性质,结合图象即可解答;④利用待定系数法求出a、b、c,代入解一元二次方程即可解答.
三、解答题
19.【答案】 解:把点A(-4,8)代入y=ax2,得:
16a=8
∴a=
∴y= x2.
再把点B(2,n)代入y= x2得:
n=2.
∴B(2,2).
【考点】二次函数的定义,待定系数法求二次函数解析式,二次函数图象上点的坐标特征
【解析】【分析】 把点A(-4,8)代入y=ax2,即可求出a的值;再把a的值和点B(2,n)代入y= a x2可求出n的值,即求出了B的坐标。
20.【答案】 解:∵抛物线的顶点坐标为 A(2,﹣3),
∴可设抛物线解析式为 y=a(x﹣2)2﹣3, 将 B(0,5)代入,得 4a﹣3=5,
解得 a=2,
∴抛物线的解析式为 y=2(x﹣2)2﹣3 化为一般式为 y=2x2﹣8x+5
【考点】待定系数法求二次函数解析式
【解析】【分析】 利用抛物线的顶点坐标为 A(2,﹣3),可设抛物线顶点式y=a(x﹣2)2﹣3,将 B(0,5)代入解析式中,求出a值即可.
21.【答案】 解:设二次函数的表达式为 ,
把点(-1,0), (3,0)和(0,3)代入,则
,
解得: ,
∴二次函数的表达式为: .
【考点】待定系数法求二次函数解析式
【解析】【分析】设二次函数的表达式为 ,把点(-1,0), (3,0)和(0,3)代入,即可求出表达式.
22.【答案】 解:把A(﹣1,8)、B(2,﹣1),C(0,3)都代入y=ax2+bx+c中,得
,
解得 ,
∴二次函数的解析式为:y=x2﹣4x+3.
【考点】待定系数法求二次函数解析式
【解析】【分析】把三个点的坐标分别代入解析式得三元一次方程组,解方程组便可得出a、b、c的值,进而得解析式.
23.【答案】 解:由题意,设 ,
∵抛物线过点(3,0),
∴ ,
解得 ,
∴
即 .
【考点】待定系数法求二次函数解析式
【解析】【分析】由于已知抛物线的顶点坐标,则可设顶点式y=a(x-1)2+2,然后把(3,0)代入求出a即可.
24.【答案】 解:∵y= (x+h)2 ,
∴当x=0时,y= h2 , 则C(0, h2),
当y=0时, (x+h)2=0,解得x=﹣h,则A(﹣h,0),
∵OA=OC,
∴﹣h= h2 , 解得h=0(舍去)或h=﹣2,
∴抛物线解析式为y= (x﹣2)2
【考点】待定系数法求二次函数解析式
【解析】【分析】先根据坐标轴上点的坐标特征用h表示A点和C点坐标得A(﹣h,0),C(0, h2),再利用OA=OC得到﹣h= h2 , 解关于h的方程求出h即可得到抛物线的解析式.
25.【答案】 解:由题意可得二次函数的顶点坐标为(﹣1,﹣4),
设二次函数的解析式为:y=a(x+1)2﹣4,
把点(0,﹣3)代入y=a(x+1)2﹣4,得a=1,
故抛物线解析式为y=(x+1)2﹣4,即y=x2+2x﹣3.
【考点】待定系数法求二次函数解析式
【解析】【分析】利用表中数据和抛物线的对称性可得到二次函数的顶点坐标为(﹣1,﹣4),则可设顶点式y=a(x+1)2﹣4,然后把点(0,﹣3)代入求出a即可.
26.【答案】 解:(1)解:∵y=x+3与坐标轴分别交与A,B两点,∴A点坐标(-3,0)、B点坐标(0,3).
∵抛物线y=ax2+bx-3a经过A,B两点,
∴
解得
∴抛物线解析式为:y=-x2-2x+3.
∵y=-x2-2x+3=-(x+1)2+4,
∴顶点C的坐标为(-1,4).
(2)证明:∵B,D关于MN对称,C(-1,4),B(0,3),
∴D(-2,3).∵B(0,3),A(-3,0),∴OA=OB.
又∠AOB=90°,∴∠ABO=∠BAO=45°.
∵B,D关于MN对称,∴BD⊥MN.
又∵MN⊥x轴,∴BD∥x轴.
∴∠DBA=∠BAO=45°.
∴∠DBO=∠DBA+∠ABO=45°+45°=90°.
设直线BC的解析式为y=kx+b,
把B(0,3),C(-1,4)代入得,
解得
∴y=-x+3.
当y=0时,-x+3=0,x=3,∴E(3,0).
∴OB=OE,又∵∠BOE=90°,
∴∠OEB=∠OBE=∠BAO=45°.
∴∠ABE=180°-∠BAE-∠BEA=90°.
∴∠ABC=180°-∠ABE=90°.
∴∠CBD=∠ABC-∠ABD=45°.
∵CM⊥BD,∴∠MCB=45°.
∵B,D关于MN对称,
∴∠CDM=∠CBD=45°,CD∥AB.
又∵AD与BC不平行,∴四边形ABCD是梯形.
∵∠ABC=90°,∴四边形ABCD是直角梯形.
【考点】待定系数法求二次函数解析式
【解析】【分析】考查待定系数法求二次函数解析式。
27.【答案】 解:(1)将B、C两点的坐标代入得
解得:;
所以二次函数的表达式为:y=x2﹣2x﹣3.
(2)存在点P,使四边形POPC为菱形;
设P点坐标为(x,x2﹣2x﹣3),PP′交CO于E
若四边形POP′C是菱形,则有PC=PO;
连接PP′,则PE⊥CO于E,
∴OE=EC=
∴y=-;
∴x2﹣2x﹣3=-
解得:=,=(不合题意,舍去)
∴P点的坐标为( , -)
(3)过点P作y轴的平行线与BC交于点Q,与OB交于点F,设P(x,x2﹣2x﹣3),
易得,直线BC的解析式为y=x﹣3则Q点的坐标为(x,x﹣3);
S四边形ABPC=S△ABC+S△BPQ+S△CPQ=AB OC+QP OF+QP BF=×4×3+=-+
当x=时,四边形ABPC的面积最大
此时P点坐标为( , -)四边形ABPC的面积的最大值为.
【考点】待定系数法求二次函数解析式
【解析】【分析】(1)将B、C的坐标代入抛物线的解析式中即可求得待定系数的值;
(2)由于菱形的对角线互相垂直平分,若四边形POP′C为菱形,那么P点必在OC的垂直平分线上,据此可求出P点的纵坐标,代入抛物线的解析式中即可求出P点的坐标;
(3) 由于△ABC的面积为定值,当四边形ABPC的面积最大时,△BPC的面积最大;过P作y轴的平行线,交直线BC于Q,交x轴于F,易求得直线BC的解析 式,可设出P点的横坐标,然后根据抛物线和直线BC的解析式求出Q、P的纵坐标,即可得到PQ的长,以PQ为底,B点横坐标的绝对值为高即可求得△BPC 的面积,由此可得到关于四边形ACPB的面积与P点横坐标的函数关系式,根据函数的性质即可求出四边形ABPC的最大面积及对应的P点坐标.
28.【答案】 (1)解:∵抛物线y=x2+ax+b经过点A(-2,0),B(-1,3),
∴ ,
解得 ,
∴y=x2+6x+8.
(2)解:∵y=x2+6x+8=(x+3)2-1,
∴顶点C坐标为(-3,-1),
∵B(-1,3).
∴OB2=12+32=10,OC2=32+12=10,BC2=[(-3)-(-1)]2+(-1-3)2=20,
∴OB2+OC2=BC2 ,
则△OBC是以BC为斜边的直角三角形,
∴∠BOC=90°.
【考点】待定系数法求二次函数解析式,勾股定理,勾股定理的逆定理
【解析】【分析】(1)将A、B点的坐标代入抛物线方程,建立关于a、b的方程,计算参数,即可得出答案。
(2)结合抛物线方程,分别得出B、C的坐标,分别计算出OB、OC、BC的长度,结合勾股定理,即可得出答案。
(
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
(
第
1
页 共
3
页
)
一、单选题
1.若二次函数y=ax2的图象经过点p(-2 , 4),则该图象必经过点( )
A. (2, 4) B. (-2, - 4) C. (- 4, 2) D. (4, -2)
2.二次函数的图象如图所示,则这个二次函数的解析式为( )
A. y= (x﹣2)2+3 B. y= (x﹣2)2﹣3
C. y=﹣ (x﹣2)2+3 D. y=﹣ (x﹣2)2﹣3
3.已知二次函数的图象如图所示,则这个二次函数的表达式为( )
A. B. C. D.
4.如图,是一条抛物线的图象,则其解析式为( )
A. y=x2﹣2x+3 B. y=x2﹣2x﹣3 C. y=x2+2x+3 D. y=x2+2x-3
5.若二次函数y=ax2+bx+c的x与y对应值如下表:则当x=1时,y的值为( ).
A. 5 B. -3 C. -13 D. -27
6.已知二次函数y=ax2+bx+c的图象上部分点的横坐标x与纵坐标y的对应值如下表:
x … -1 0 1 2 …
y … 0 3 4 3 …
那么关于它的图象,下列判断正确的是( )
A. 开口向上 B. 与x轴的另一个交点是(3,0)
C. 与y轴交于负半轴 D. 在直线x=1的左侧部分是下降的
7.已知点A(1,1) 、B(3,1) 、C(4,2) 、D(2,2), 若抛物线y=ax2(a>0)与四边形ABCD的边没有交点,则a的取值范围为( )
A. < a< 1 B. < a< 1 C. a>l或0< a< D. a>1或0
A. y=-2 B. y=2 C. y= - D. y=
9.某同学在用描点法画二次函数y=ax2+bx+c的图象时,列出了下面的表格:由于粗心,他算错了其中一个y值,则这个错误的数值是( )
A. ﹣11 B. ﹣2 C. 1 D. ﹣5
10.如图, 在平面直角坐标系中, 矩形O ABC的点B坐标为(8, 6) ,点A在x轴上,点C在y轴上.点D是边AB上的动点,连接OD,作点A关于线段OD的对称点A'.已知一条抛物线y=ax +bx+c(a≠0)经过O,A',A三点,且点A'恰好是抛物线的顶点,则b的值为( )
A. - B. 2 C. -2 D.
二、填空题
11.若一个二次函数的二次项系数为-1,且图象的顶点坐标为(0,-3).则这个二次函数的表达式为 .
12.请写出一个对称轴为x=1的抛物线的解析式________.
13.已知二次函数y=ax2的图象经过点A(-2, ).则该函数的解析式为________.
14.抛物线 过点A(2,3),则此抛物线开口向________.
15.一条抛物线的顶点是A(2,1),且经过点B(1,0),则该抛物线的函数表达式是 .
16.抛物线y=2x2+3x+k﹣2经过点(﹣1,0),那么k= .
17.若二次函数 的图象经过点(-1,0),(1,-2),当 随 的增大而增大时, 的取值范围是 。
18.二次函数 为常数, 中的 与 的部分对应值如下表:
x -1 0 3
y n -3 -3
当 时,下列结论中一定正确的是 (填序号即可)
① ;②当 时, 的值随 值的增大而增大;③ ;④当 时,关于 的一元二次方程 的解是 , .
三、解答题
19.如图,已知点A(-4,8)和点B(2,n)在抛物线y=ax2上.求a的值及点B的坐标.
20.已知抛物线的顶点是 A(2,﹣3),且交 y 轴于点 B(0,5),求此抛物线的解析式.
21.已知二次函数的图象与x轴交于点(-1,0)和 (3,0),并且与y轴交于点(0,3).求这个二次函数表达式.
22.二次函数y=ax2+bx+c(a≠0)的图象过点A(﹣1,8)、B(2,﹣1),与y轴交于点C(0,3),求二次函数的表达式.
23.已知抛物线的顶点坐标 且过点 ,求该抛物线的解析式.
24.二次函数y= (x+h)2的图象如图所示,已知OA=OC,试求该抛物线的解析式.
25.已知一个二次函数图象上部分点的横坐标x与纵坐标y的对应值如表所示:
x …… ﹣3 ﹣2 ﹣1 0 1 ……
y …… 0 ﹣3 ﹣4 ﹣3 0 ……
求这个二次函数的表达式.
26.如图,直线y=x+3与坐标轴分别交于A,B两点,抛物线y=ax2+bx-3a经过点A,B,顶点为C,连接CB并延长交x轴于点E,点D与点B关于抛物线的对称轴MN对称.
(1)求抛物线的解析式及顶点C的坐标;
(2)求证:四边形ABCD是直角梯形.
27.如图,在平面直角坐标系中,二次函数y=+bx+c的图象与x轴交于A、B两点, A点在原点的左侧,B点的坐标为(3,0),与y轴交于C(0,-3)点,点P是直线BC下方的抛物线上一动点.
(1)求这个二次函数的表达式.
(2)连结PO、PC,并把△POC沿CO翻折,得到四边形POP’C,那么是否存在点P,使四边形POP’C为菱形?若存在,请求出此时点P的坐标;若不存在,请说明理由.
(3)当点P运动到什么位置时,四边形 ABPC的面积最大并求出此时P点的坐标和四边形ABPC的最大面积.
28.如图,在平面直角坐标系xOy中,抛物线y=x2+ax+b经过点A(-2,0),B(-1,3).
(1)求抛物线的解析式;
(2)设抛物线的顶点为C,直接写出点C的坐标和∠BOC的度数.
答案解析部分
一、单选题
1.【答案】 B
【考点】待定系数法求二次函数解析式
【解析】【解答】解:AC、由题意得:-4=a(-2)2, 解得a=-1, ∴y=-x2, ∴y≤0,AC不符合题意;
BD、当x=-2时,y=-x2=-4, 当x=4时,y=-16,∴ B符合题意,D不符合题意;
故答案为:B.
【分析】先把P代入函数,求出a值,得y=-x2≤0,排除不符合项,再代入点的坐标即可确定图象必过之点.
2.【答案】 C
【考点】待定系数法求二次函数解析式
【解析】【解答】解:抛物线开口向下,顶点是(2,3),所以y=﹣ (x﹣2)2+3,
故答案为:C.
【分析】根据二次函数的开口方向向下和顶点坐标即可判断。
3.【答案】 B
【考点】待定系数法求二次函数解析式
【解析】【解答】根据题意,图象与y轴交于负半轴,故c为负数,又四个选项中,B、C的c为-3,符合题意,故设二次函数的表达式为y=ax2+bx+c,
抛物线过(-1,0),(0,-3),(3,0),
所以
解得a=1,b=-2,c=-3,
这个二次函数的表达式为y=x2-2x-3.
故答案为:B.
【分析】根据题意,把抛物线经过的三点代入函数的表达式,列出方程组,解出各系数则可
4.【答案】 B
【考点】待定系数法求二次函数解析式
【解析】【解答】解:因为抛物线与x轴的交点坐标为(-1,0),(3,0),
可设交点式为y=a(x+1)(x-3),
把(0,-3)代入y=a(x+1)(x-3),
可得:-3=a(0+1)(0-3),
解得:a=1,
所以解析式为:y=x2-2x-3,
故答案为:B.
【分析】观察图象可知抛物线与x轴和y轴的两个交点坐标,于是可将抛物线的解析式设为交点式,再把抛物线与y轴的交点坐标代入解析式计算即可求解.
5.【答案】 C
【考点】待定系数法求二次函数解析式
【解析】
【分析】由表可知,抛物线的对称轴为直线x=-3,顶点坐标为(-3,5),再用待定系数法求得二次函数的解析式,再把x=0代入即可求得y的值.
【解答】设二次函数的解析式为y=a(x-h)2+k,
∵当x=-4或-2时,y=3,由抛物线的对称性可知h=-3,k=5,
∴y=a(x+3)2+5,
把(-2,3)代入得,a=-2,
∴二次函数的解析式为y=-2(x+3)2+5,
当x=0时,y=-13.
故选C.
6.【答案】 B
【考点】待定系数法求二次函数解析式,二次函数y=ax^2+bx+c的性质
【解析】【解答】A、由表格知,抛物线的顶点坐标是(1,4).故设抛物线解析式为y=a(x﹣1)2+4.
将(﹣1,0)代入,得
a(﹣1﹣1)2+4=0,
解得a=﹣2.
∵a=﹣2<0,
∴抛物线的开口方向向下,
故本选项不符合题意;
B、抛物线与x轴的一个交点为(﹣1,0),对称轴是x=1,则抛物线与x轴的另一个交点是(3,0),故本选项符合题意;
C、由表格知,抛物线与y轴的交点坐标是(0,3),即与y轴交于正半轴,故本选项不符合题意;
D、抛物线开口方向向下,对称轴为x=1,则在直线x=1的左侧部分是上升的,故本选项不符合题意;
故答案为:B.
【分析】(1)由表格中的信息可知,抛物线的顶点坐标是(1,4),所以设抛物线解析式为y=a(x﹣1)2+4;将(﹣1,0)代入,解得a=﹣2,而﹣2<0,所以抛物线的开口方向向下;
(2)由(1)知,对称轴是x=1,所以根据已知点抛物线与x轴的一个交点为(﹣1,0)可得抛物线与x轴的另一个交点是(3,0);
(3)由表格中的信息可知,抛物线与y轴的交点坐标是(0,3),即与y轴交于正半轴;
(4)由(1)知,抛物线开口方向向下,对称轴为x=1,则在直线x=1的左侧部分是上升的。
7.【答案】 D
【考点】待定系数法求二次函数解析式,二次函数y=ax^2+bx+c的图象
【解析】【解答】解:如图所示:把A(1,1)代入y=ax2得,a=1,
把B(3,1)代入y=ax2得a= ,
∵抛物线的开口越小,|a|的绝对值越大,
∴抛物y=ax2与四边形ABCD的边没有交点,则a的取值范围为:a>1或0
【分析】先求出a= ,再根据抛物线的开口越小,|a|的绝对值越大,求解即可。
8.【答案】 C
【考点】待定系数法求二次函数解析式
【解析】【解答】抛物线顶点为(0,0),所以设抛物线方程为 (2,-2)是图像上的点,所以
故答案为:C
【分析】根据抛物线的顶点是原点,对称轴是1由轴,解析式可设为由题意知,点(2,-2)在抛物线上,利用待定系数法求出解析式即可。
9.【答案】 D
【考点】待定系数法求二次函数解析式
【解析】【解答】解:由已知数据可得函数图象关于y轴对称,则不符合题意应出现在x=-2或x=2时,
故函数的顶点坐标为(0,1),
,
当x=1时, 解得 ,
当 时, ,
∴错误的数值是-5,
故答案为:D。
【分析】由已知可得函数图像关于y轴对称,则不符合题意应该出现在x=-2或x=2时,根据正确的数据求出函数的解析式,进而可得答案。
10.【答案】 B
【考点】坐标与图形性质,待定系数法求二次函数解析式,矩形的性质,轴对称的性质,二次函数图象上点的坐标特征
【解析】【解答】如图,过点A'作A'E⊥OA于E,连接A'O,A'A,
∵ 矩形O ABC的点B坐标为(8, 6) ,∴OA=8,
∵ 点A关于线段OD的对称点A',∴A'O=OA,
∵抛物线y=ax +bx+c(a≠0)经过O,A',A三点,且点A'恰好是抛物线的顶点,
∴A'O=A'A,∴A'O=A'A=OA,∴△A'AO是等边三角形,
∴A'O=A'A=OA=8,
∵A'E⊥OA,∴OE=AO=4,
∴A'A==4 , ∴A'(4,4),
∵ 点A'是抛物线的顶点,
∴设 y=a(x-4) +4,
将点O(0,0)代入解析式中,得a=,
∴y=(x-4) +4=x2+2x,
∴b=2.
【分析】如图,过点A'作A'E⊥OA于E,连接A'O,A'A,根据矩形及轴对称的性质,可得A'O=OA=8,利用抛物线y=ax +bx+c(a≠0)经过O,A',A三点,且点A'恰好是抛物线的顶点,可得△A'AO是等边三角形,从而可得OE=AO=4,利用勾股定理求出A'A==4 , 可得A'(4,4),从而可得设y=a(x-4) +4,将点O(0,0)代入解析式中求出a值,可得y=(x-4) +4=x2+2x,据此即可求出结论.
二、填空题
11.【答案】 y=﹣x2﹣3
【考点】待定系数法求二次函数解析式
【解析】【解答】解:∵抛物线二次项系数为-1,顶点坐标为(0,-3),
∴抛物线的顶点式为y=-(x-0)2-3,即y=-x2-3;
故答案是y=-x2-3。
【分析】把抛物线设为顶点式,化为一般式即可.
12.【答案】 y=(x﹣1)2
【考点】待定系数法求二次函数解析式
【解析】【解答】解:抛物线y=(x﹣1)2的对称轴为直线x=1.
故答案为:y=(x﹣1)2 .
【分析】利用二次函数的性质写出一个顶点的横坐标为1的抛物线解析式即可.
13.【答案】
【考点】待定系数法求二次函数解析式
【解析】【解答】解:将点A(-2,- )代入y=ax2得a= ,
∴该函数的解析式为 ,
故答案为 : .
【分析】将点A(-2,- )代入y=ax2即可得到a的值.
14.【答案】 上
【考点】待定系数法求二次函数解析式,二次函数y=ax^2+bx+c的性质
【解析】【解答】解:∵抛物线 过点A(2,3),
∴4a-8+3=3
∴a=2>0
∴此抛物线开口向上
故答案为:上
【分析】将点A的坐标代入抛物线的解析式可得4a-8+3=3,求出a的值再判断开口方向即可。
15.【答案】 (或 )
【考点】待定系数法求二次函数解析式
【解析】【解答】设抛物线解析式为y=a(x-2)2+1,
把B(1,0)代入得a+1=0,解得a=-1,
所以抛物线解析式为y=-(x-2)2+1,即y=-x2+4x-3
故答案为: (或y=-x2+4x-3).
【分析】已知抛物线的顶点坐标,因此设函数解析式为顶点式,再将点B的坐标代入计算,即可得出函数解析式。
16.【答案】 3
【考点】待定系数法求二次函数解析式
【解析】【解答】∵抛物线y=2x2+3x+k-2经过点(-1,0),
∴0=2-3+k-2,
解得k=3.
故答案为:3.
【分析】将已知点的坐标代入函数解析式,建立关于k的方程,求解即可。
17.【答案】 x>
【考点】待定系数法求二次函数解析式,二次函数y=ax^2+bx+c的性质,二次函数y=ax^2+bx+c与二次函数y=a(x-h)^2+k的转化
【解析】【解答】将(-1,0),(1,-2)代入函数解析式得 解得
则函数解析式为y=x2-x-2=(x- )2- ,
根据抛物线性质可知当x> 时,函数值y随x的增大而增大.
故答案为:x>
【分析】分别将(-1,0),(1,-2)代入函数解析式,得出关于B,C的二元一次方程组,求解得出b,c的值,从而求出抛物线的解析式,再将解析式配成顶点式,由于此函数的二次项系数大于0,图像开口向上,顶点右侧y随x的增大而增大,从而得出答案。
18.【答案】 ①②④
【考点】待定系数法求二次函数解析式,二次函数y=ax^2+bx+c的图象,二次函数y=ax^2+bx+c的性质
【解析】【解答】解:由表格数据知,二次函数的对称轴为 ,且c=-3<0,
∵n>0,∴a>0,
∵对称轴 >0,
∴b<0即 bc>0,故①正确;
∵a>0,对称轴为 ,
∴当x> 时, 的值随 值的增大而增大,
∴当 时, 的值随 值的增大而增大,
故②正确;
③由对称轴 得:b=-3a,
∴
∵当x=-1时,y=n,
∴n=a+3a-3=4a-3,
∴n﹤4a,故③错误;
④当n=1时,将(-1,1),(0,-3),(3,-3)代入函数解析式中,得:
,
解得 ,
∴关于x的一元二次方程为 ,解得 , ,
故④正确,
故答案为:①②④.
【分析】①根据表格数据得到对称轴为 ,c=-3<0,又n>0知a>0,即可得出答案;②根据二次函数的性质即可解答;③根据二次函数的性质,结合图象即可解答;④利用待定系数法求出a、b、c,代入解一元二次方程即可解答.
三、解答题
19.【答案】 解:把点A(-4,8)代入y=ax2,得:
16a=8
∴a=
∴y= x2.
再把点B(2,n)代入y= x2得:
n=2.
∴B(2,2).
【考点】二次函数的定义,待定系数法求二次函数解析式,二次函数图象上点的坐标特征
【解析】【分析】 把点A(-4,8)代入y=ax2,即可求出a的值;再把a的值和点B(2,n)代入y= a x2可求出n的值,即求出了B的坐标。
20.【答案】 解:∵抛物线的顶点坐标为 A(2,﹣3),
∴可设抛物线解析式为 y=a(x﹣2)2﹣3, 将 B(0,5)代入,得 4a﹣3=5,
解得 a=2,
∴抛物线的解析式为 y=2(x﹣2)2﹣3 化为一般式为 y=2x2﹣8x+5
【考点】待定系数法求二次函数解析式
【解析】【分析】 利用抛物线的顶点坐标为 A(2,﹣3),可设抛物线顶点式y=a(x﹣2)2﹣3,将 B(0,5)代入解析式中,求出a值即可.
21.【答案】 解:设二次函数的表达式为 ,
把点(-1,0), (3,0)和(0,3)代入,则
,
解得: ,
∴二次函数的表达式为: .
【考点】待定系数法求二次函数解析式
【解析】【分析】设二次函数的表达式为 ,把点(-1,0), (3,0)和(0,3)代入,即可求出表达式.
22.【答案】 解:把A(﹣1,8)、B(2,﹣1),C(0,3)都代入y=ax2+bx+c中,得
,
解得 ,
∴二次函数的解析式为:y=x2﹣4x+3.
【考点】待定系数法求二次函数解析式
【解析】【分析】把三个点的坐标分别代入解析式得三元一次方程组,解方程组便可得出a、b、c的值,进而得解析式.
23.【答案】 解:由题意,设 ,
∵抛物线过点(3,0),
∴ ,
解得 ,
∴
即 .
【考点】待定系数法求二次函数解析式
【解析】【分析】由于已知抛物线的顶点坐标,则可设顶点式y=a(x-1)2+2,然后把(3,0)代入求出a即可.
24.【答案】 解:∵y= (x+h)2 ,
∴当x=0时,y= h2 , 则C(0, h2),
当y=0时, (x+h)2=0,解得x=﹣h,则A(﹣h,0),
∵OA=OC,
∴﹣h= h2 , 解得h=0(舍去)或h=﹣2,
∴抛物线解析式为y= (x﹣2)2
【考点】待定系数法求二次函数解析式
【解析】【分析】先根据坐标轴上点的坐标特征用h表示A点和C点坐标得A(﹣h,0),C(0, h2),再利用OA=OC得到﹣h= h2 , 解关于h的方程求出h即可得到抛物线的解析式.
25.【答案】 解:由题意可得二次函数的顶点坐标为(﹣1,﹣4),
设二次函数的解析式为:y=a(x+1)2﹣4,
把点(0,﹣3)代入y=a(x+1)2﹣4,得a=1,
故抛物线解析式为y=(x+1)2﹣4,即y=x2+2x﹣3.
【考点】待定系数法求二次函数解析式
【解析】【分析】利用表中数据和抛物线的对称性可得到二次函数的顶点坐标为(﹣1,﹣4),则可设顶点式y=a(x+1)2﹣4,然后把点(0,﹣3)代入求出a即可.
26.【答案】 解:(1)解:∵y=x+3与坐标轴分别交与A,B两点,∴A点坐标(-3,0)、B点坐标(0,3).
∵抛物线y=ax2+bx-3a经过A,B两点,
∴
解得
∴抛物线解析式为:y=-x2-2x+3.
∵y=-x2-2x+3=-(x+1)2+4,
∴顶点C的坐标为(-1,4).
(2)证明:∵B,D关于MN对称,C(-1,4),B(0,3),
∴D(-2,3).∵B(0,3),A(-3,0),∴OA=OB.
又∠AOB=90°,∴∠ABO=∠BAO=45°.
∵B,D关于MN对称,∴BD⊥MN.
又∵MN⊥x轴,∴BD∥x轴.
∴∠DBA=∠BAO=45°.
∴∠DBO=∠DBA+∠ABO=45°+45°=90°.
设直线BC的解析式为y=kx+b,
把B(0,3),C(-1,4)代入得,
解得
∴y=-x+3.
当y=0时,-x+3=0,x=3,∴E(3,0).
∴OB=OE,又∵∠BOE=90°,
∴∠OEB=∠OBE=∠BAO=45°.
∴∠ABE=180°-∠BAE-∠BEA=90°.
∴∠ABC=180°-∠ABE=90°.
∴∠CBD=∠ABC-∠ABD=45°.
∵CM⊥BD,∴∠MCB=45°.
∵B,D关于MN对称,
∴∠CDM=∠CBD=45°,CD∥AB.
又∵AD与BC不平行,∴四边形ABCD是梯形.
∵∠ABC=90°,∴四边形ABCD是直角梯形.
【考点】待定系数法求二次函数解析式
【解析】【分析】考查待定系数法求二次函数解析式。
27.【答案】 解:(1)将B、C两点的坐标代入得
解得:;
所以二次函数的表达式为:y=x2﹣2x﹣3.
(2)存在点P,使四边形POPC为菱形;
设P点坐标为(x,x2﹣2x﹣3),PP′交CO于E
若四边形POP′C是菱形,则有PC=PO;
连接PP′,则PE⊥CO于E,
∴OE=EC=
∴y=-;
∴x2﹣2x﹣3=-
解得:=,=(不合题意,舍去)
∴P点的坐标为( , -)
(3)过点P作y轴的平行线与BC交于点Q,与OB交于点F,设P(x,x2﹣2x﹣3),
易得,直线BC的解析式为y=x﹣3则Q点的坐标为(x,x﹣3);
S四边形ABPC=S△ABC+S△BPQ+S△CPQ=AB OC+QP OF+QP BF=×4×3+=-+
当x=时,四边形ABPC的面积最大
此时P点坐标为( , -)四边形ABPC的面积的最大值为.
【考点】待定系数法求二次函数解析式
【解析】【分析】(1)将B、C的坐标代入抛物线的解析式中即可求得待定系数的值;
(2)由于菱形的对角线互相垂直平分,若四边形POP′C为菱形,那么P点必在OC的垂直平分线上,据此可求出P点的纵坐标,代入抛物线的解析式中即可求出P点的坐标;
(3) 由于△ABC的面积为定值,当四边形ABPC的面积最大时,△BPC的面积最大;过P作y轴的平行线,交直线BC于Q,交x轴于F,易求得直线BC的解析 式,可设出P点的横坐标,然后根据抛物线和直线BC的解析式求出Q、P的纵坐标,即可得到PQ的长,以PQ为底,B点横坐标的绝对值为高即可求得△BPC 的面积,由此可得到关于四边形ACPB的面积与P点横坐标的函数关系式,根据函数的性质即可求出四边形ABPC的最大面积及对应的P点坐标.
28.【答案】 (1)解:∵抛物线y=x2+ax+b经过点A(-2,0),B(-1,3),
∴ ,
解得 ,
∴y=x2+6x+8.
(2)解:∵y=x2+6x+8=(x+3)2-1,
∴顶点C坐标为(-3,-1),
∵B(-1,3).
∴OB2=12+32=10,OC2=32+12=10,BC2=[(-3)-(-1)]2+(-1-3)2=20,
∴OB2+OC2=BC2 ,
则△OBC是以BC为斜边的直角三角形,
∴∠BOC=90°.
【考点】待定系数法求二次函数解析式,勾股定理,勾股定理的逆定理
【解析】【分析】(1)将A、B点的坐标代入抛物线方程,建立关于a、b的方程,计算参数,即可得出答案。
(2)结合抛物线方程,分别得出B、C的坐标,分别计算出OB、OC、BC的长度,结合勾股定理,即可得出答案。
(
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
(
第
1
页 共
3
页
)
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
