2021-2022学年苏科版数学八年级上册6.2一次函数基础练习(word版含答案)
文档属性
| 名称 | 2021-2022学年苏科版数学八年级上册6.2一次函数基础练习(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 44.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
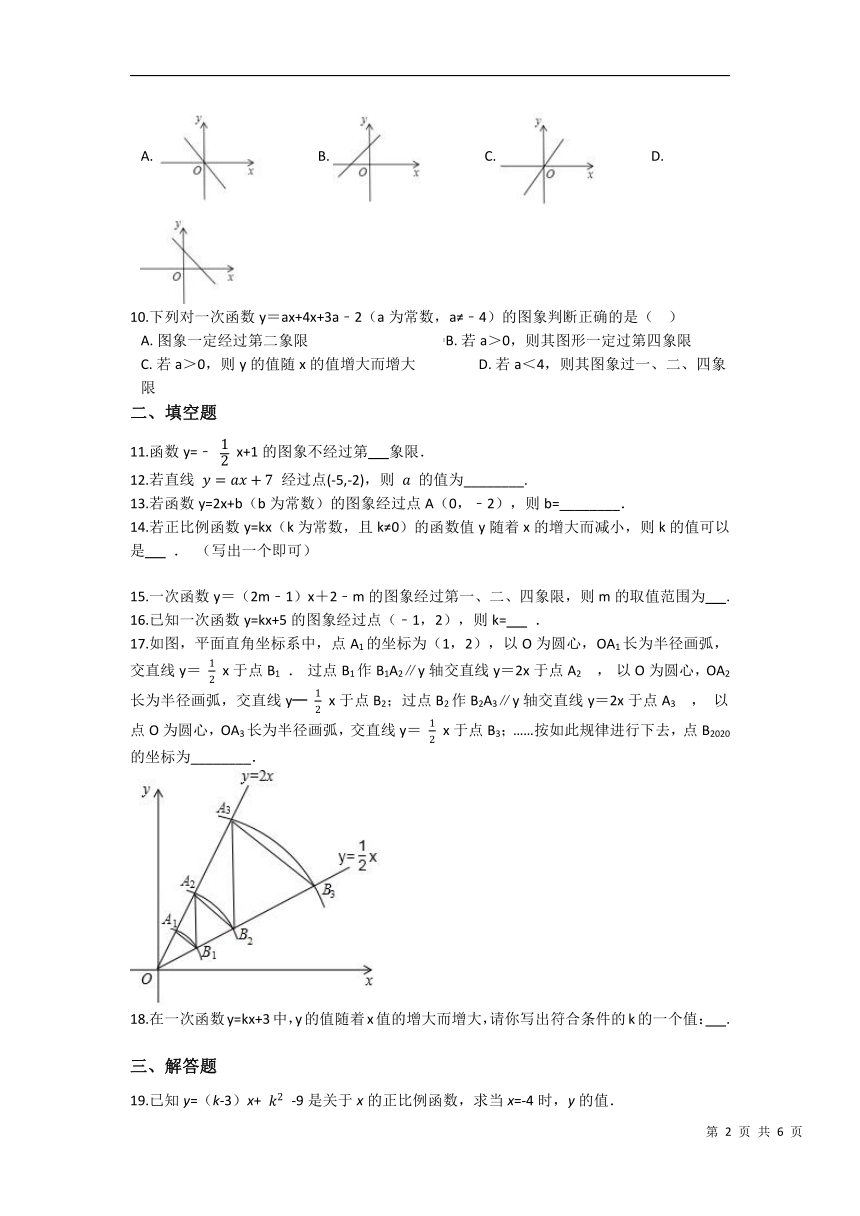
| 科目 | 数学 | ||
| 更新时间 | 2021-12-04 21:01:33 | ||
图片预览


文档简介
6.2一次函数基础练习
一、单选题
1.已知一次函数 图象如图所示,点 在图象上,则 与 的大小关系为( )
A. B. C. D.
2.函数y=(k2﹣1)x+3k是一次函数,则k的取值范围是( )
A. k≠﹣1 B. k≠1 C. k≠±1 D. k为一切实数
3.正比例函数 y=(k-2)x 中,y 随 x 的增大而减小,则 k 的取值范围是( )
A. k≥2 B. k≤2 C. k>2 D. k<2
4.点P1( , ),点P2( , )是一次函数=-4 + 3 图象上的两个点,且< , 则1与2的大小关系是( )
A. > B. >>0 C. < D. <
5.下列函数:①y=﹣πx,②y=﹣0.125x,③y=8,④y=﹣8x2+6,⑤y=﹣0.5x﹣1中,一次函数有( )
A. 1个 B. 2个 C. 3个 D. 4个
6.已知一次函数 ( 为常数)的图象经过平面直角坐标系的第一、二、三象限,则下列结论一定正确的是( )
A. B. C. D.
7.已知关于x的一次函数 , 其中实数k满足0<k<1,当自变量x在2≤x≤3范围内时,此函数的最大值为
A. 1 B. 2 C. k D.
8.若一元二次方程x2﹣2x﹣m=0无实数根,则一次函数y=(m+1)x+m﹣1的图象不经过第( )象限
A. 四 B. 三 C. 二 D. 一
9.已知正比例函数y=kx (k≠0),当x=-1时,y=-2,则它的图象大致是( ).
A. B. C. D.
10.下列对一次函数y=ax+4x+3a﹣2(a为常数,a≠﹣4)的图象判断正确的是( )
A. 图象一定经过第二象限 B. 若a>0,则其图形一定过第四象限
C. 若a>0,则y的值随x的值增大而增大 D. 若a<4,则其图象过一、二、四象限
二、填空题
11.函数y=﹣ x+1的图象不经过第 象限.
12.若直线 经过点(-5,-2),则 的值为________.
13.若函数y=2x+b(b为常数)的图象经过点A(0,﹣2),则b=________.
14.若正比例函数y=kx(k为常数,且k≠0)的函数值y随着x的增大而减小,则k的值可以是 . (写出一个即可)
15.一次函数y=(2m﹣1)x+2﹣m的图象经过第一、二、四象限,则m的取值范围为 .
16.已知一次函数y=kx+5的图象经过点(﹣1,2),则k= .
17.如图,平面直角坐标系中,点A1的坐标为(1,2),以O为圆心,OA1长为半径画弧,交直线y= x于点B1 . 过点B1作B1A2∥y轴交直线y=2x于点A2 , 以O为圆心,OA2长为半径画弧,交直线y═ x于点B2;过点B2作B2A3∥y轴交直线y=2x于点A3 , 以点O为圆心,OA3长为半径画弧,交直线y= x于点B3;……按如此规律进行下去,点B2020的坐标为________.
18.在一次函数y=kx+3中,y的值随着x值的增大而增大,请你写出符合条件的k的一个值: .
三、解答题
19.已知y=(k-3)x+ -9是关于x的正比例函数,求当x=-4时,y的值.
20.已知正比例函数y=(2-k)x的图象经过第二、四象限,则函数y=-kx的图象经过哪些象限?
21.已知一次函数 中,y随x的增大而减小,且其图象与y轴交点在x轴上方.求m的取值范围.
22.已知正比例函数y=(m+2)x中,y的值随x的增大而增大,而正比例函数y=(2m-3)x , y的值随x的增大而减小,且m为整数,你能求出吗?为什么?
23.拖拉机开始工作时,油箱中有油40升,如果工作每小时耗油4升,求:
(1)油箱中的余油量Q(升)与工作时间t(时)的函数关系式及自变量的取值范围;
(2)当工作5小时时油箱的余油量
24.已知y+3和2x-1成正比例,且x=2时,y=1。
(1)写出y与x的函数解析式。
(2)当0≤x≤3 时,y的最大值和最小值分别是多少?
25.已知正比例函数y=(3k﹣1)x,若y随x的增大而增大,求k的取值范围.
26.已知函数y=(m-3)x|m|-2+3是一次函数,求解析式.
27.已知:y=(k-1)x|k|+k2-4是一次函数,求(3k+2)2007的值.
28.已知一次函数y=(2m+4)x+(3-n).当m、n是什么数时,y随x的增大而增大.
答案解析部分
一、单选题
1.【答案】 A
【考点】一次函数的性质
2.【答案】 C
【考点】一次函数的定义
3.【答案】 D
【考点】正比例函数的图象和性质
4.【答案】 A
【考点】一次函数的性质
5.【答案】 C
【考点】一次函数的定义
6.【答案】 A
【考点】一次函数图象、性质与系数的关系
7.【答案】 D
【考点】一次函数的性质
8.【答案】 D
【考点】一次函数图象、性质与系数的关系
9.【答案】 C
【考点】正比例函数的图象和性质
10.【答案】 C
【考点】一次函数图象、性质与系数的关系
二、填空题
11.【答案】 三
【考点】正比例函数的图象和性质
12.【答案】
【考点】一次函数的性质
13.【答案】 -2
【考点】一次函数的性质
14.【答案】 -2
【考点】正比例函数的图象和性质
15.【答案】 m<
【考点】一次函数图象、性质与系数的关系
16.【答案】 3
【考点】一次函数的性质
17.【答案】 (22020 , 22019)
【考点】点的坐标,正比例函数的图象和性质
18.【答案】 2
【考点】一次函数的性质
三、解答题
19.【答案】 解:当 -9=0,且k-3≠0时,y是x的正比例函数,故k=-3时,y是x的正比例函数,∴y=-6x,当x=-4时,y=-6×(-4)=24
【考点】正比例函数的图象和性质
20.【答案】 解:∵正比例函数经过二、四象限,
∴2-k<0,
∴k>2,
∴-k<0,
∴ 函数y=-kx的图象经过二、四象限.
故答案为: 第二、四象限.
【考点】正比例函数的图象和性质
21.【答案】 解:∵一次函数y随x的增大而减小∴ 又∵其图象与y轴交点在x轴上方m+1>0 ∴m的取值范围是:
【考点】一次函数的性质
22.【答案】 解:m的可能值为-1,0,1.理由如下:∵正比例函数y=(m+2)x中,y的值随x的增大而增大,∴m+2>0,解得m>-2.∵正比例函数y=(2m-3)x,y的值随x的增大而减小,∴2m-3<0,解得m<1.5.∵m为整数,∴m的可能值为-1,0,1
【考点】正比例函数的图象和性质
23.【答案】 解:(1)由题意可知:Q=40﹣4t(0≤t≤10);
(2)把t=5时代入Q=40﹣4t得:油箱的余油量Q=20升.
【考点】一次函数图象、性质与系数的关系
24.【答案】 (1)解:∵y+3和2x-1成正比例,
∴设y+3=(2x-1)k,
把x=2,y=1代入得:4=3k,
解得:k= ,
即y+3= (2x-1),
函数解析式为y= x-
(2)解:把x=0,代入y= x- 得,y=- ,
把x=3,代入y= x- 得,y= ,
所以当0≤x≤3时,y的最大值 ,y的最小值-
【考点】正比例函数的图象和性质
25.【答案】 解:根据y随x的增大而增大,知:3k﹣1>0,
解得k> .
故k的取值范围为k> .
【考点】正比例函数的图象和性质
26.【答案】 解答: ∵m-3≠0且|m|-2=1,∴m=-3,∴函数解析式为:y=-6x+3
【考点】绝对值及有理数的绝对值,一次函数的定义
27.【答案】 解答:由题意得:|k|=1且k-1≠0,解得:k=-1,(3k+2)2007=(-3+2)2007=-1
【考点】一次函数的定义
28.【答案】 解答: 2m+4>0,即m>-2,n为任何实数时,y随x的增大而增大.
(
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
【考点】一次函数的性质 (
第
1
页 共
3
页
)
一、单选题
1.已知一次函数 图象如图所示,点 在图象上,则 与 的大小关系为( )
A. B. C. D.
2.函数y=(k2﹣1)x+3k是一次函数,则k的取值范围是( )
A. k≠﹣1 B. k≠1 C. k≠±1 D. k为一切实数
3.正比例函数 y=(k-2)x 中,y 随 x 的增大而减小,则 k 的取值范围是( )
A. k≥2 B. k≤2 C. k>2 D. k<2
4.点P1( , ),点P2( , )是一次函数=-4 + 3 图象上的两个点,且< , 则1与2的大小关系是( )
A. > B. >>0 C. < D. <
5.下列函数:①y=﹣πx,②y=﹣0.125x,③y=8,④y=﹣8x2+6,⑤y=﹣0.5x﹣1中,一次函数有( )
A. 1个 B. 2个 C. 3个 D. 4个
6.已知一次函数 ( 为常数)的图象经过平面直角坐标系的第一、二、三象限,则下列结论一定正确的是( )
A. B. C. D.
7.已知关于x的一次函数 , 其中实数k满足0<k<1,当自变量x在2≤x≤3范围内时,此函数的最大值为
A. 1 B. 2 C. k D.
8.若一元二次方程x2﹣2x﹣m=0无实数根,则一次函数y=(m+1)x+m﹣1的图象不经过第( )象限
A. 四 B. 三 C. 二 D. 一
9.已知正比例函数y=kx (k≠0),当x=-1时,y=-2,则它的图象大致是( ).
A. B. C. D.
10.下列对一次函数y=ax+4x+3a﹣2(a为常数,a≠﹣4)的图象判断正确的是( )
A. 图象一定经过第二象限 B. 若a>0,则其图形一定过第四象限
C. 若a>0,则y的值随x的值增大而增大 D. 若a<4,则其图象过一、二、四象限
二、填空题
11.函数y=﹣ x+1的图象不经过第 象限.
12.若直线 经过点(-5,-2),则 的值为________.
13.若函数y=2x+b(b为常数)的图象经过点A(0,﹣2),则b=________.
14.若正比例函数y=kx(k为常数,且k≠0)的函数值y随着x的增大而减小,则k的值可以是 . (写出一个即可)
15.一次函数y=(2m﹣1)x+2﹣m的图象经过第一、二、四象限,则m的取值范围为 .
16.已知一次函数y=kx+5的图象经过点(﹣1,2),则k= .
17.如图,平面直角坐标系中,点A1的坐标为(1,2),以O为圆心,OA1长为半径画弧,交直线y= x于点B1 . 过点B1作B1A2∥y轴交直线y=2x于点A2 , 以O为圆心,OA2长为半径画弧,交直线y═ x于点B2;过点B2作B2A3∥y轴交直线y=2x于点A3 , 以点O为圆心,OA3长为半径画弧,交直线y= x于点B3;……按如此规律进行下去,点B2020的坐标为________.
18.在一次函数y=kx+3中,y的值随着x值的增大而增大,请你写出符合条件的k的一个值: .
三、解答题
19.已知y=(k-3)x+ -9是关于x的正比例函数,求当x=-4时,y的值.
20.已知正比例函数y=(2-k)x的图象经过第二、四象限,则函数y=-kx的图象经过哪些象限?
21.已知一次函数 中,y随x的增大而减小,且其图象与y轴交点在x轴上方.求m的取值范围.
22.已知正比例函数y=(m+2)x中,y的值随x的增大而增大,而正比例函数y=(2m-3)x , y的值随x的增大而减小,且m为整数,你能求出吗?为什么?
23.拖拉机开始工作时,油箱中有油40升,如果工作每小时耗油4升,求:
(1)油箱中的余油量Q(升)与工作时间t(时)的函数关系式及自变量的取值范围;
(2)当工作5小时时油箱的余油量
24.已知y+3和2x-1成正比例,且x=2时,y=1。
(1)写出y与x的函数解析式。
(2)当0≤x≤3 时,y的最大值和最小值分别是多少?
25.已知正比例函数y=(3k﹣1)x,若y随x的增大而增大,求k的取值范围.
26.已知函数y=(m-3)x|m|-2+3是一次函数,求解析式.
27.已知:y=(k-1)x|k|+k2-4是一次函数,求(3k+2)2007的值.
28.已知一次函数y=(2m+4)x+(3-n).当m、n是什么数时,y随x的增大而增大.
答案解析部分
一、单选题
1.【答案】 A
【考点】一次函数的性质
2.【答案】 C
【考点】一次函数的定义
3.【答案】 D
【考点】正比例函数的图象和性质
4.【答案】 A
【考点】一次函数的性质
5.【答案】 C
【考点】一次函数的定义
6.【答案】 A
【考点】一次函数图象、性质与系数的关系
7.【答案】 D
【考点】一次函数的性质
8.【答案】 D
【考点】一次函数图象、性质与系数的关系
9.【答案】 C
【考点】正比例函数的图象和性质
10.【答案】 C
【考点】一次函数图象、性质与系数的关系
二、填空题
11.【答案】 三
【考点】正比例函数的图象和性质
12.【答案】
【考点】一次函数的性质
13.【答案】 -2
【考点】一次函数的性质
14.【答案】 -2
【考点】正比例函数的图象和性质
15.【答案】 m<
【考点】一次函数图象、性质与系数的关系
16.【答案】 3
【考点】一次函数的性质
17.【答案】 (22020 , 22019)
【考点】点的坐标,正比例函数的图象和性质
18.【答案】 2
【考点】一次函数的性质
三、解答题
19.【答案】 解:当 -9=0,且k-3≠0时,y是x的正比例函数,故k=-3时,y是x的正比例函数,∴y=-6x,当x=-4时,y=-6×(-4)=24
【考点】正比例函数的图象和性质
20.【答案】 解:∵正比例函数经过二、四象限,
∴2-k<0,
∴k>2,
∴-k<0,
∴ 函数y=-kx的图象经过二、四象限.
故答案为: 第二、四象限.
【考点】正比例函数的图象和性质
21.【答案】 解:∵一次函数y随x的增大而减小∴ 又∵其图象与y轴交点在x轴上方m+1>0 ∴m的取值范围是:
【考点】一次函数的性质
22.【答案】 解:m的可能值为-1,0,1.理由如下:∵正比例函数y=(m+2)x中,y的值随x的增大而增大,∴m+2>0,解得m>-2.∵正比例函数y=(2m-3)x,y的值随x的增大而减小,∴2m-3<0,解得m<1.5.∵m为整数,∴m的可能值为-1,0,1
【考点】正比例函数的图象和性质
23.【答案】 解:(1)由题意可知:Q=40﹣4t(0≤t≤10);
(2)把t=5时代入Q=40﹣4t得:油箱的余油量Q=20升.
【考点】一次函数图象、性质与系数的关系
24.【答案】 (1)解:∵y+3和2x-1成正比例,
∴设y+3=(2x-1)k,
把x=2,y=1代入得:4=3k,
解得:k= ,
即y+3= (2x-1),
函数解析式为y= x-
(2)解:把x=0,代入y= x- 得,y=- ,
把x=3,代入y= x- 得,y= ,
所以当0≤x≤3时,y的最大值 ,y的最小值-
【考点】正比例函数的图象和性质
25.【答案】 解:根据y随x的增大而增大,知:3k﹣1>0,
解得k> .
故k的取值范围为k> .
【考点】正比例函数的图象和性质
26.【答案】 解答: ∵m-3≠0且|m|-2=1,∴m=-3,∴函数解析式为:y=-6x+3
【考点】绝对值及有理数的绝对值,一次函数的定义
27.【答案】 解答:由题意得:|k|=1且k-1≠0,解得:k=-1,(3k+2)2007=(-3+2)2007=-1
【考点】一次函数的定义
28.【答案】 解答: 2m+4>0,即m>-2,n为任何实数时,y随x的增大而增大.
(
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
【考点】一次函数的性质 (
第
1
页 共
3
页
)
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
