22.3 实际问题与二次函数 训练2021-2022学年人教版九年级数学上册(word版含答案)
文档属性
| 名称 | 22.3 实际问题与二次函数 训练2021-2022学年人教版九年级数学上册(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 270.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-04 21:12:34 | ||
图片预览



文档简介
人教版九年级数学上册22.3实际问题与二次函数训练
一、单选题
1.如图,矩形ABCD中,AB=6cm,BC=3cm,动点P从A点出发以1cm/秒向终点B运动,动点Q同时从A点出发以2cm/秒按A→D→C→B的方向在边AD,DC,CB上运动,设运动时间为x(秒),那么△APQ的面积y(cm2)随着时间x(秒)变化的函数图象大致为( )
A. B.
C. D.
2.某超市将进货单价为l8元的商品按每件20元销售时,每日可销售100件,如果每件提价1元,日销售就要减少10件,那么把商品的售出价定为多少元时,才能使每天获得的利润最大?( )
A.22元 B.24元 C.26元 D.28元
3.记某商品销售单价为x元,商家销售此种商品每月获得的销售利润为y元,且y是关于x的二次函数.已知当商家将此种商品销售单价分别定为55元或75元时,他每月均可获得销售利润1800元;当商家将此种商品销售单价定为80元时,他每月可获得销售利润1550元,则y与x的函数关系式是( )
A.y=﹣(x﹣60)2+1825 B.y=﹣2(x﹣60)2+1850
C.y=﹣(x﹣65)2+1900 D.y=﹣2(x﹣65)2+2000
4.某种花卉每盆的盈利与每盆的株数有一定的关系,每盆植3株时,平均每株盈利4元;若每盆增加1株,平均每株盈利减少0.5元,要使每盆的盈利达到15元,每盆应多植多少株?设每盆多植x株,则可以列出的方程是( )
A.(3+x)(4-0.5x)=15 B.(x+3)(4+0.5x)=15
C.(x+4)(3-0.5x)=15 D.(x+1)(4-0.5x)=15
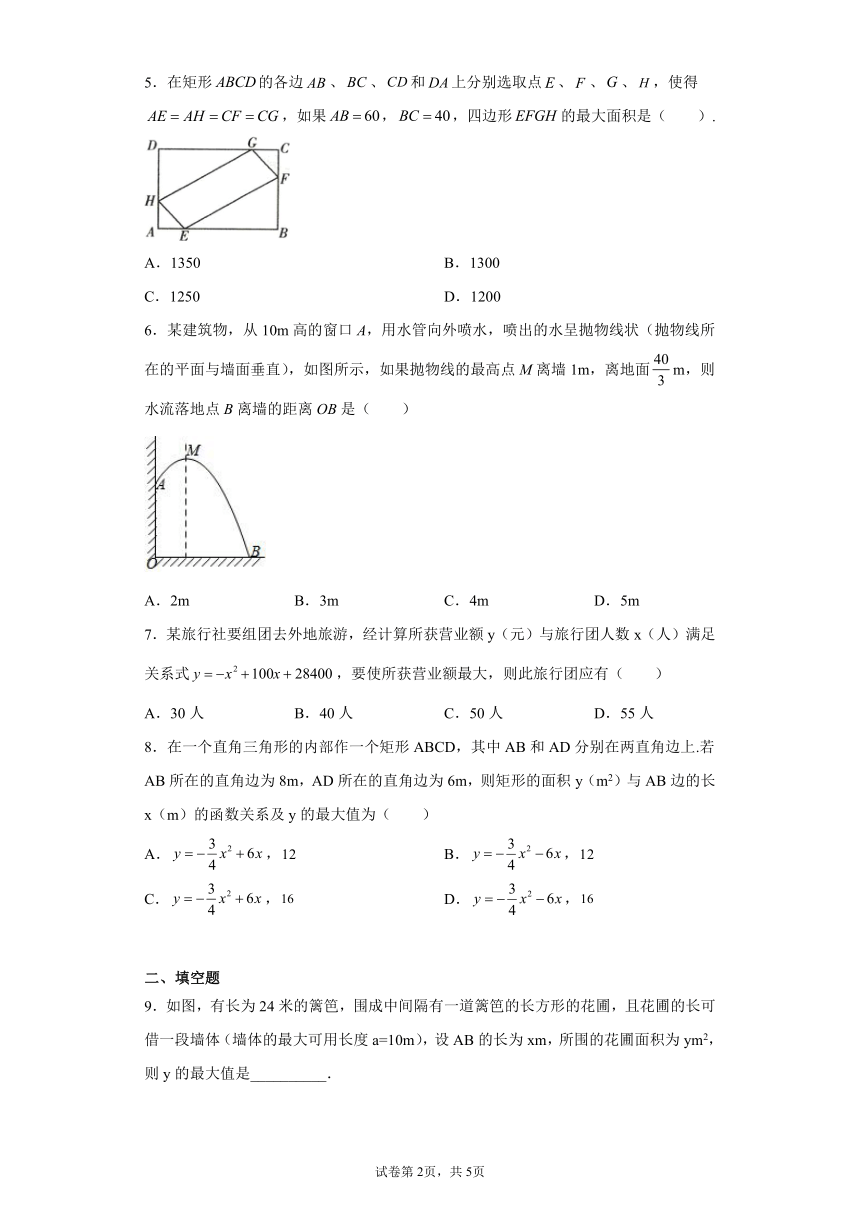
5.在矩形的各边、、和上分别选取点、、、,使得,如果,,四边形的最大面积是( ).
A.1350 B.1300
C.1250 D.1200
6.某建筑物,从10m高的窗口A,用水管向外喷水,喷出的水呈抛物线状(抛物线所在的平面与墙面垂直),如图所示,如果抛物线的最高点M离墙1m,离地面m,则水流落地点B离墙的距离OB是( )
A.2m B.3m C.4m D.5m
7.某旅行社要组团去外地旅游,经计算所获营业额y(元)与旅行团人数x(人)满足关系式,要使所获营业额最大,则此旅行团应有( )
A.30人 B.40人 C.50人 D.55人
8.在一个直角三角形的内部作一个矩形ABCD,其中AB和AD分别在两直角边上.若AB所在的直角边为8m,AD所在的直角边为6m,则矩形的面积y(m2)与AB边的长x(m)的函数关系及y的最大值为( )
A., B.,
C., D.,
二、填空题
9.如图,有长为24米的篱笆,围成中间隔有一道篱笆的长方形的花圃,且花圃的长可借一段墙体(墙体的最大可用长度a=10m),设AB的长为xm,所围的花圃面积为ym2,则y的最大值是__________.
10.某网店销售一款李宁牌运动服,每件进价元,若按每件元出售,每天可卖出件,根据市场调查结果,若每件降价元,则每天可多卖出件,要使每天获得的利润最大,则每件需要降价的钱数为________元.
11.一根长为40cm的铁丝,把它弯成一个矩形框,设矩形的长为xcm,矩形的面积为y(cm2),试写出y与x的函数关系式:________.(注意标注自变量x的取值范围)
12.一个小球被抛出后,距离地面的高度h(m)和飞行时间t(s)满足下面函数解析式:h=-5t2+10t+1,则小球距离地面的最大高度是________m.
13.已知实数x,y满足,则的最大值是______.
14.如果二次函数y=x2﹣4x+m﹣1的顶点在x轴上,那么m=_____.
15.二次函数图象的顶点坐标是(﹣1,4),且过点(2,﹣5),则这个二次函数的表达式是_____.
16.已知老王一个月销售某种服装(件)与获得利润(元)满足关系式:,则当一个月卖出________件衣服时,获得最大利润________元.
三、解答题
17.如图所示,在中,,厘米,.点从点开始沿边向点以厘米/秒的速度移动,点从点开始沿边向点以厘米/秒的速度移动,当点运动到点时停止,点也同时停止.
(1)如果点,分别从点,同时出发,那么几秒后,的面积等于平方厘米?
(2)如果点,分别从点,同时出发,问第几秒时,四边形的面积最小?其最小面积为多少?
18. 如图,已知抛物线经过A(2,0)、B(0,-6)两点,其对称轴与轴交于点C
(1)求该抛物线和直线BC的解析式;
(2)设抛物线与直线BC相交于点D,连结AB、AD,求△ABD的面积.
19.某商场有A,B两种商品,若买2件A商品和1件B商品,共需80元;若买3件A商品和2件B商品,共需135元.
(1)设A,B两种商品每件售价分别为a元、b元,求a、b的值;
(2)B商品每件的成本是20元,根据市场调查:若按(1)中求出的单价销售,该商场每天销售B商品100件;若销售单价每上涨1元,B商品每天的销售量就减少5件.
①求每天B商品的销售利润y(元)与销售单价(x)元之间的函数关系?
②求销售单价为多少元时,B商品每天的销售利润最大,最大利润是多少?
20.某机械租赁公司有同一型号的机械设备40套,经过一段时间的经营发现:当每套机械设备的月租金为270元时,恰好全部租出,在此基础上,当每套设备的月租金提高10元时,这种设备就少租一套,且未租出一套设备每月需要支出费用(维护费、管理费等)20元.
(1)设每套设备的月租金为(元),用含的代数式表示未租出的设备数(套)以及所有未租出设备(套)的支出费用;
(2)租赁公司的月收益能否达到11040元?此时应该出租多少套机械设备?每套月租金是多少元?请简要说明理由;
(3)租赁公司的月收益能否在11040元基础上再提高?为什么?
参考答案
1.A
2.B
3.D
4.A
5.C
6.B
7.C
8.A
9.;
10.4
11.y=﹣x2+20x(10≤x<20)
12.6
13.10
14.5
15.y=﹣(x+1)2+4
16.
17.(1)1秒;(2)秒,
18.(1);;(2)
19.(1)a=25,b=30;(2)①y=-5+350x-5000;②35元时,最大利润为1125元.
20.(1)未租出的设备为套,所有未租出设备的支出费用为元;(2)当月租金300元,租出37套;或月租金350元,租出32套,该公司的月收益为11040元;(3)可获得比11040元更高的月收益
试卷第2页,共2页
试卷第1页,共1页
一、单选题
1.如图,矩形ABCD中,AB=6cm,BC=3cm,动点P从A点出发以1cm/秒向终点B运动,动点Q同时从A点出发以2cm/秒按A→D→C→B的方向在边AD,DC,CB上运动,设运动时间为x(秒),那么△APQ的面积y(cm2)随着时间x(秒)变化的函数图象大致为( )
A. B.
C. D.
2.某超市将进货单价为l8元的商品按每件20元销售时,每日可销售100件,如果每件提价1元,日销售就要减少10件,那么把商品的售出价定为多少元时,才能使每天获得的利润最大?( )
A.22元 B.24元 C.26元 D.28元
3.记某商品销售单价为x元,商家销售此种商品每月获得的销售利润为y元,且y是关于x的二次函数.已知当商家将此种商品销售单价分别定为55元或75元时,他每月均可获得销售利润1800元;当商家将此种商品销售单价定为80元时,他每月可获得销售利润1550元,则y与x的函数关系式是( )
A.y=﹣(x﹣60)2+1825 B.y=﹣2(x﹣60)2+1850
C.y=﹣(x﹣65)2+1900 D.y=﹣2(x﹣65)2+2000
4.某种花卉每盆的盈利与每盆的株数有一定的关系,每盆植3株时,平均每株盈利4元;若每盆增加1株,平均每株盈利减少0.5元,要使每盆的盈利达到15元,每盆应多植多少株?设每盆多植x株,则可以列出的方程是( )
A.(3+x)(4-0.5x)=15 B.(x+3)(4+0.5x)=15
C.(x+4)(3-0.5x)=15 D.(x+1)(4-0.5x)=15
5.在矩形的各边、、和上分别选取点、、、,使得,如果,,四边形的最大面积是( ).
A.1350 B.1300
C.1250 D.1200
6.某建筑物,从10m高的窗口A,用水管向外喷水,喷出的水呈抛物线状(抛物线所在的平面与墙面垂直),如图所示,如果抛物线的最高点M离墙1m,离地面m,则水流落地点B离墙的距离OB是( )
A.2m B.3m C.4m D.5m
7.某旅行社要组团去外地旅游,经计算所获营业额y(元)与旅行团人数x(人)满足关系式,要使所获营业额最大,则此旅行团应有( )
A.30人 B.40人 C.50人 D.55人
8.在一个直角三角形的内部作一个矩形ABCD,其中AB和AD分别在两直角边上.若AB所在的直角边为8m,AD所在的直角边为6m,则矩形的面积y(m2)与AB边的长x(m)的函数关系及y的最大值为( )
A., B.,
C., D.,
二、填空题
9.如图,有长为24米的篱笆,围成中间隔有一道篱笆的长方形的花圃,且花圃的长可借一段墙体(墙体的最大可用长度a=10m),设AB的长为xm,所围的花圃面积为ym2,则y的最大值是__________.
10.某网店销售一款李宁牌运动服,每件进价元,若按每件元出售,每天可卖出件,根据市场调查结果,若每件降价元,则每天可多卖出件,要使每天获得的利润最大,则每件需要降价的钱数为________元.
11.一根长为40cm的铁丝,把它弯成一个矩形框,设矩形的长为xcm,矩形的面积为y(cm2),试写出y与x的函数关系式:________.(注意标注自变量x的取值范围)
12.一个小球被抛出后,距离地面的高度h(m)和飞行时间t(s)满足下面函数解析式:h=-5t2+10t+1,则小球距离地面的最大高度是________m.
13.已知实数x,y满足,则的最大值是______.
14.如果二次函数y=x2﹣4x+m﹣1的顶点在x轴上,那么m=_____.
15.二次函数图象的顶点坐标是(﹣1,4),且过点(2,﹣5),则这个二次函数的表达式是_____.
16.已知老王一个月销售某种服装(件)与获得利润(元)满足关系式:,则当一个月卖出________件衣服时,获得最大利润________元.
三、解答题
17.如图所示,在中,,厘米,.点从点开始沿边向点以厘米/秒的速度移动,点从点开始沿边向点以厘米/秒的速度移动,当点运动到点时停止,点也同时停止.
(1)如果点,分别从点,同时出发,那么几秒后,的面积等于平方厘米?
(2)如果点,分别从点,同时出发,问第几秒时,四边形的面积最小?其最小面积为多少?
18. 如图,已知抛物线经过A(2,0)、B(0,-6)两点,其对称轴与轴交于点C
(1)求该抛物线和直线BC的解析式;
(2)设抛物线与直线BC相交于点D,连结AB、AD,求△ABD的面积.
19.某商场有A,B两种商品,若买2件A商品和1件B商品,共需80元;若买3件A商品和2件B商品,共需135元.
(1)设A,B两种商品每件售价分别为a元、b元,求a、b的值;
(2)B商品每件的成本是20元,根据市场调查:若按(1)中求出的单价销售,该商场每天销售B商品100件;若销售单价每上涨1元,B商品每天的销售量就减少5件.
①求每天B商品的销售利润y(元)与销售单价(x)元之间的函数关系?
②求销售单价为多少元时,B商品每天的销售利润最大,最大利润是多少?
20.某机械租赁公司有同一型号的机械设备40套,经过一段时间的经营发现:当每套机械设备的月租金为270元时,恰好全部租出,在此基础上,当每套设备的月租金提高10元时,这种设备就少租一套,且未租出一套设备每月需要支出费用(维护费、管理费等)20元.
(1)设每套设备的月租金为(元),用含的代数式表示未租出的设备数(套)以及所有未租出设备(套)的支出费用;
(2)租赁公司的月收益能否达到11040元?此时应该出租多少套机械设备?每套月租金是多少元?请简要说明理由;
(3)租赁公司的月收益能否在11040元基础上再提高?为什么?
参考答案
1.A
2.B
3.D
4.A
5.C
6.B
7.C
8.A
9.;
10.4
11.y=﹣x2+20x(10≤x<20)
12.6
13.10
14.5
15.y=﹣(x+1)2+4
16.
17.(1)1秒;(2)秒,
18.(1);;(2)
19.(1)a=25,b=30;(2)①y=-5+350x-5000;②35元时,最大利润为1125元.
20.(1)未租出的设备为套,所有未租出设备的支出费用为元;(2)当月租金300元,租出37套;或月租金350元,租出32套,该公司的月收益为11040元;(3)可获得比11040元更高的月收益
试卷第2页,共2页
试卷第1页,共1页
同课章节目录
