第6章一次函数基础练习 2021-2022学年苏科版数学八年级上册(word版含答案)
文档属性
| 名称 | 第6章一次函数基础练习 2021-2022学年苏科版数学八年级上册(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 89.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-04 21:23:24 | ||
图片预览




文档简介
一次函数基础练习
一、单选题
1.下列四个备选项中,其中有一个选项的内容从表达形式上看不属于函数,则这一个选项是( )
A. y= B. y=3x+1 C. y=-2x +x-1 D.
2.当自变量x=3时,函数y=﹣x﹣3的函数值为( )
A. 0 B. 9 C. 6 D. ﹣6
3.函数y= 中,自变量x的取值范围是( )
A. x>2 B. x≠2 C. x>-1 D. x≠-1
4.下列函数中,是一次函数的是( )
A. B. C. y=5x2+x D. y= 8
5.下列图象不能表示函数关系的是( )
A. B. C. D.
6.函数 的自变量 的取值范围是( )
A. B. C. D. ,且
7.函数 的图象如图所示,则函数 的大致图象是( )
A. B. C. D.
8.某汽车从A开往360km外的B,全程的前一部分为高速公路,后一部分为普通公路.若汽车在高速公路和普通公路上分别以某一速度匀速行驶,汽车行驶的路程y(单位:km)与时间x(单位:h)之间的关系如图所示,则下列结论正确的是( )
A. 汽车在高速公路上的行驶速度为100km/h B. 普通公路总长为90km
C. 汽车在普通公路上的行驶速度为60km/h D. 汽车出发后4h到B地
9.已知:直线y= x+ (n为正整数)与两坐标轴围成的三角形面积为Sn , 则S1+S2+S3+…+S2019( )
A. B. C. D.
10.如图,等腰Rt△ABC中,BC= ,以边AC为斜边向右做等腰Rt△ACD,点E是线段CD的中点,连接 AE.作线段CE关于直线AC的对称线段CF,连接BF,并延长BF交线段AE于点G,则线段BG长为( )
A. B. C. D.
二、填空题
11.球的表面积S与半径R之间的关系是S=4πR2 . 对于各种不同大小的圆,请指出公式S=4πR2中常量是 ,变量是
12.在一次函数y=-2(x+1)+x中,一次项系数k为________,常数项b为________.
13.函数y= 自变量x的取值范围是________.
14.若函数y= 有意义,则自变量x的取值范围是 .
15.在函数y= 中,自变量x的取值范围是 .
16.小亮拿15元钱去文具店买签字笔,每支1.5元,小亮买签字笔后所剩钱数 (元)与买签字笔的支数 (支)之间的关系式为 .
17.函数y= 中,自变量x的取值范围是 .
18.已知: 、 、 是三个非负数,并且满足 , ,设 ,设 为 的最大值.则 的值为 .
三、解答题
19.已知函数 是一次函数,求m的值.
20.当k取何值时,关于x的方程2(2x-3)=1-2x和8-k=2(x+ )的解相同?
21.填表,并在同一坐标系内作出函数y=2x-5 和y=-x+1的图像;
填表:y=2x-5
x … 0 …
y … 0 …
y=-x+1
x … 0 …
y … 0 …
22.已知一次函数 中,y随x的增大而减小,且其图象与y轴交点在x轴上方.求m的取值范围.
23.已知弹簧的长度y(厘米)在一定的限度内是所挂物质量x(千克)的一次函数.现已测得不挂重物时弹簧的长度是6厘米,挂4千克质量的重物时,弹簧的长度是7. 2厘米,求这个一次函数的关系式.
24.已知两个变量x、y满足关系2x﹣3y+1=0,试问:①y是x的函数吗?②x是y的函数吗?若是,写出y与x的关系式,若不是,说明理由.
25.某校餐厅计划购买12张餐桌和一批餐椅,现从甲、乙两商场了解到:同一型号的餐桌报价每张均为200元,餐椅报价每把均为50元.甲商场称:每购买一张餐桌赠送一把餐椅;乙商场规定:所有餐桌椅均按报价的八五折销售.那么,学校应如何购买更优惠?
26.如图,直线y=﹣2x+6与直线y=mx+n相交于点M(p,4).
(1)求p的值;
(2)直接写出关于x,y的二元一次方程组的解;
(3)判断直线y=3nx+m﹣2n是否也过点M?并说明理由.
27.已知:y=(k-1)x|k|+k2-4是一次函数,求(3k+2)2007的值.
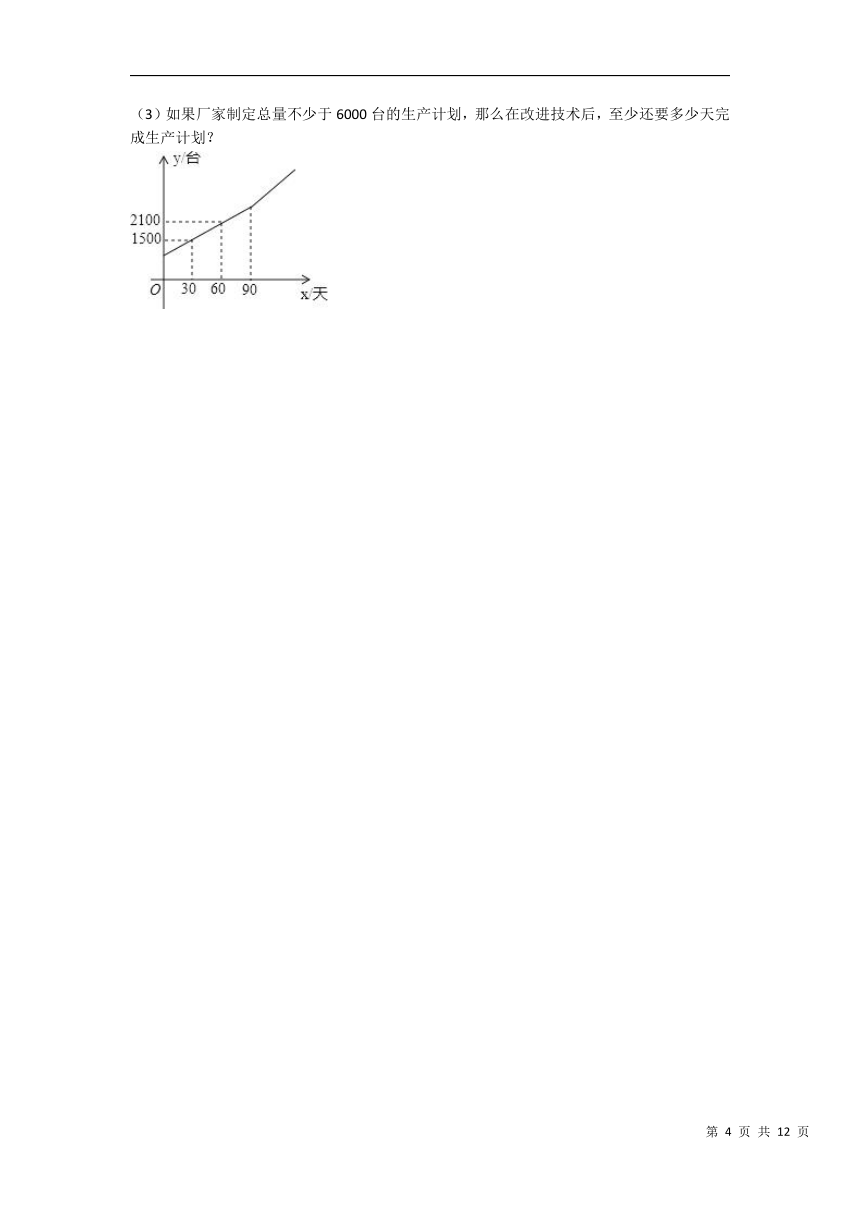
28.随着生活质量的提高,人们健康意识逐渐增强,安装净水设备的百姓家庭越来越多.某厂家从去年开始投入生产净水器,生产净水器的总量y(台)与今年的生产天数x(天)的关系如图所示.今年生产90天后,厂家改进了技术,平均每天的生产数量达到30台.
(1)求y与x之间的函数表达式;
(2)已知该厂家去年平均每天的生产数量与今年前90天平均每天的生产数量相同,求厂家去年生产的天数;
(3)如果厂家制定总量不少于6000台的生产计划,那么在改进技术后,至少还要多少天完成生产计划?
答案解析部分
一、单选题
1.【答案】 D
【考点】函数的概念
【解析】【解答】解:A、 , y是x的函数,故A不符合题意;
B、y=3x+1,y是x的一次函数,故B不符合题意;
C、 y=-2x +x-1,y是x的二次函数,故C不符合题意;
D、 , 这是关于x的分式方程,表示函数,故D符合题意;
故答案为:D.
【分析】利用函数的定义:一般地,在一个变化过程中,如果有两个变量x与y,并且对于x的每一个确定的值,y都有惟一确定的值与其对应,那么我们就说x是自变量,y是x的函数,再对各选项逐一判断。
2.【答案】 D
【考点】函数值
【解析】【解答】解:当x=3时,y=﹣1×3﹣3=﹣6.
故答案为:D.
【分析】代入x=3求出与之对应的y值,此题得解.
3.【答案】 D
【考点】函数自变量的取值范围
【解析】【解答】解:根据题意可得x+1≠0;
解得x≠-1;
故答案为:D.
【分析】这是一个自变量在分母的函数,须分母不为0,求出自变量的取值范围x≠-1。
4.【答案】 B
【考点】一次函数的定义
【解析】【解答】解: 是反比例函数,故A不符合题意;
是一次函数,也是正比例函数,故B符合题意;
y=5x2+x,是二次函数,故C不符合题意;
y= 8不是一次函数,故D不符合题意;
故答案为:B.
【分析】根据一次函数的定义逐项判定即可。
5.【答案】 A
【考点】函数的图象
【解析】【解答】解:如图所示,
作x轴的垂线,与图象有两个交点,所以y不是x的函数;
B、C、D作x轴的任意一条垂线,与图象均只有一个交点,所以B、C、D中y是x的函数.
故答案为:A.
【分析】根据函数里一个x值对应一个y值,可判断图像是否是函数。
6.【答案】 A
【考点】函数自变量的取值范围
【解析】【解答】解:函数 的自变量 的取值范围是: ,
故答案为:A.
【分析】观察含自变量的式子,含有分式,只需分母不等于0,可求出x的取值范围.
7.【答案】 B
【考点】一次函数图象、性质与系数的关系
【解析】【解答】解:由函数y=ax+b-2的图象可得:a<0,b-2=0,
∴a<0,b=2>0,
所以函数y=-ax-b的大致图象经过第一、四、三象限,
故答案为:B.
【分析】根据一次函数的图象的性质确定a和b的符号,进而解答即可.
8.【答案】 C
【考点】函数的图象
【解析】【解答】解:由题意可得,
汽车在高速公路上行驶速度为:180÷2=90km/h,故选项A错误,
普通公路的总长为:360﹣180=180km,故选项B错误,
汽车在普通公路上行驶的速度为:(270﹣180)÷(3.5﹣2)=60km/h,故选项C正确,
汽车出发后到达B地的时间为:2+(360﹣180)÷60=5h,故选项D错误,
故选C.
【分析】根据题意和图象可以分别计算出各个选项中的量,从而可以判断哪个选项是正确的,从而可以解答本题.
9.【答案】 D
【考点】一次函数的图象,三角形的面积
【解析】【解答】解:∵当n=1时,直线为y= x+ ,
∴直线与两坐标轴的交点为(0, ),(-1,0),
∴S1= ×1× = ;
当n=2时,直线为y= x+ ,
∴直线与两坐标轴的交点为(0, ),(- ,0),
∴S2= × × = × ;
当n=3时,直线为y= x+ ,
∴直线与两坐标轴的交点为(0, ),(- ,0),
∴S3= × × = × ;
…,
Sn= × ,
∴S1+S2+S3+…+S2019= ×(1- + + +…+ - )= (1- )=
故答案为:D.
【分析】依次求出S1、S2、S3 , 就发现规律:Sn= × ,然后求其和即可求得答案.注意 .
10.【答案】 B
【考点】点的坐标,一次函数的实际应用
【解析】【解答】解:建立如图所示坐标系,使BC与x轴重合,AC与y轴重合,
∵ ABC和 ACD都是等腰直角三角形,且BC= ,
∴AC=BC= ,AB= ,AD=CD= ,
可将各点坐标表示出来,A(0, ),B( ,0),C(0,0),D( , ),
∴点E为CD中点,故E的坐标为( , ),
又∵CF为CE关于AC的对称线段,故F的坐标为( , ),
设直线BF的解析式为:y=kx+b,将B点、F点坐标代入,
,解得: ,
∴直线BF的解析式为: ,
设直线AE的解析式为:y=mx+n,将A点、E点坐标代入,
,解得: ,
∴直线BF的解析式为: ,
直线BF与AE相交于点G,
,解得: ,即G( , ),
线段BG的长度为: ,
故答案为:B.
【分析】建立如下图所示坐标系,使BC与x轴重合,AC与y轴重合,可将各点坐标求出,并通过两点式分别求出直线BF、直线AE的解析式,直线BF与AE相交于点G,即可求出BG的长度.
二、填空题
11.【答案】 4π;S和R
【考点】常量、变量
【解析】【解答】解:公式S=4πR2中常量是4π,变量是S和R.
故答案是:4π;S和R.
【分析】变量是指在程序的运行过程中随时可以发生变化的量,常量是数值始终不变的量,根据定义即可确定.
12.【答案】 -1;-2
【考点】一次函数的定义
【解析】【解答】解:将 y=-2(x+1)+x 变形,得:y=-x-2 ,
则k=-1;b=-2
故答案为: -1;-2.
【分析】 将一次函数y=-2(x+1)+x展开合并同类项化为y=kx+b的形式,即可看出一次项系数k和常数项b 的值.
13.【答案】 x≠4
【考点】函数自变量的取值范围
【解析】【解答】解:由题意得:4-x≠0,
∴x≠4.
故答案为:x≠4.
【分析】分式有意义的条件是分母不等于0,据此列不等式求出x的范围即可.
14.【答案】 x≠
【考点】函数自变量的取值范围
【解析】【解答】解:根据题意得:4x+1≠0,解得:x≠ .
故答案为:x≠ .
【分析】本题要求分母不能为0,因为当分母为0时,函数没有意义;
15.【答案】 x≠﹣1
【考点】函数自变量的取值范围
【解析】【解答】解:由题意,得
x+1≠0,
解得x≠﹣1,
故答案为:x≠﹣1.
【分析】分式有意义的条件为分母不为0.
16.【答案】 y=15-1.5x
【考点】根据实际问题列一次函数表达式
【解析】【解答】解:买签字笔的支数x(支)花的钱数是1.5x元,则剩余的钱数是(15-1.5x)元,
则签字笔后所剩钱数 (元)与买签字笔的支数 (支)之间的关系式为y=15-1.5x.
故答案为:y=15-1.5x.
【分析】根据小亮拿15元钱去文具店买签字笔,每支1.5元,进行求解即可。
17.【答案】 x≠﹣3
【考点】函数自变量的取值范围
【解析】【解答】解:由题意得,x+3≠0,
解得x≠﹣3.
故答案为:x≠﹣3.
【分析】根据分母不等于0列式计算即可得解.
18.【答案】
【考点】三元一次方程组解法及应用,一次函数的性质
【解析】【解答】解:3a+2b+c=6,2a+b-3c=1,
解得a=7c-4,b=9-11c;
∵a≥0、b≥0,
∴7c-4≥0,9-11c≥0,
∴ .
∵m=3a+b-7c=3c-3,
∴m随c的增大而增大,
∵ .
∴当c取最大值 ,m有最大值,
∴m的最大值为s=3× -3= .
故答案为: .
【分析】根据题意先把c看作已知数,分别用c表示出a和b ,让a≥0,b≥0 列式求出c的取值范围,再求得m用c表示的形式,结合c的取值范围即可求得s的值.
三、解答题
19.【答案】 解:∵函数 是一次函数,
∴m+2≠0且m2-3=1,
解得:m=2,
【考点】一次函数的定义
【解析】【分析】一次函数要求自变量x前的系数不等于0,指数是1,据此即可解题.
20.【答案】 解方程2(2x-3)=1-2x,得x= .把x= 代入8-k=2(x+ ),得8-k=4,即k=4.
【考点】一次函数与一元一次方程的综合应用
【解析】【分析】根据解方程,可得方程的解,根据方程的解相同,可得关于k的一元一次方程,根据解方程,可得答案.
21.【答案】 解:当x=0时,y=2×0-5=-5,当y=0时,0=2x-5,x=2.5;当x=0代入y=0+1=1,当y=0时,0=-x+1,x=1。填表如下:
x … 0 2.5 …
y … -5 0 …
x … 0 1 …
y … 1 0 …
过点(0,-5),(2.5,0)画直线,可得函数y=2x-5的图象;过点(0,1),(1,0)画直线,可得函数y=-x+1的图象。如下图:
【考点】一次函数的图象
【解析】【分析】本题考查了一次函数的图象性质,一次函数图象上点的坐标特征及图象的画法,是基础知识,需熟练掌握。
22.【答案】 解:∵一次函数y随x的增大而减小∴ 又∵其图象与y轴交点在x轴上方m+1>0 ∴m的取值范围是:
【考点】一次函数的性质
【解析】【分析】一次函数中,y随x增大而减小,说明自变量系数小于0,即2m-2<0,图象过二、四象限;又该函数的图象与y轴交点在x轴上方,据此解答m的取值范围即
23.【答案】 设所求函数的关系式是y=kx+b,
根据题意,得
解这个方程组,得
所以所求函数的关系式是y=0.3x+6
【考点】根据实际问题列一次函数表达式
【解析】【分析】已知所求函数为一次函数,可以设所求函数的关系式是y=kx+b,再由题中的已知条件代入上式,求出k、b的值,代入y=kx+b,即可求的这个一次函数的关系式.
24.【答案】 解:根据题意可知:①y= ,∵对于x的每一个取值,y都有唯一确定的值,
∴y是x的函数;
②x= ,∵对于y的每一个取值,x都有唯一确定的值,
∴x是y的函数
【考点】函数的概念,函数解析式
【解析】【分析】根据函数的定义可知,满足对于x的每一个取值,y都有唯一确定的值与之对应关系,据此即可得出答案.
25.【答案】 解:设学校购买12张餐桌和 把餐椅,到购买甲商场的费用为 元,到乙商场购买的费用为 元,则有
当 ,即 时,
答:当学校购买的餐椅少于32把时,到甲商场购买更优惠。
【考点】一次函数的实际应用,根据实际问题列一次函数表达式
【解析】【分析】 设学校购买12张餐桌和 把餐椅,到购买甲商场的费用为 元,到乙商场购买的费用为 元,根据购买的费用=购买桌子的数量×桌的单价+购买椅子的数量×椅子的单价,分别表示出y1与y2的关系式;分三种情况①当y1>y2,②y1=y2,③y1<y2时讨论即得.
26.【答案】 解:(1)∵直线y=﹣2x+6经过点M(p,4),
∴4=﹣2p+6,
∴p=1.
(2)由图象可知方程组的解为 ,
(3)结论:直线y=3nx+m﹣2n经过点M,理由如下:
∵点M(1,4)在直线y=mx+n上,
∴m+n=4,
∴当x=1,时,y=3nx+m﹣2n=m+n=4,
∴直线y=3nx+m﹣2n经过点M.
【考点】一次函数与二元一次方程(组)的综合应用
【解析】【分析】(1)根据直线y=﹣2x+6经过点M,即可求出p.
(2)由图象可知交点的坐标就是方程组的解.
(3)先求出m+n=4,用代入法可以解决.
27.【答案】 解答:由题意得:|k|=1且k-1≠0,解得:k=-1,(3k+2)2007=(-3+2)2007=-1
【考点】一次函数的定义
【解析】【分析】首先根据一次函数定义确定k的值,再代入代数式(3k+2)2007求值.
28.【答案】 解:(1)当0≤x≤90时,设y与x之间的函数关系式为y=kx+b,由函数图象,得 , 解得: . 则y=20x+900.当x>90时,由题意,得y=30x.∴y=;(2)由题意,得∵x=0时,y=900,∴去年的生产总量为900台.今年平均每天的生产量为:(2700﹣900)÷90=20台,厂家去年生产的天数为:900÷20=45天.答:厂家去年生产的天数为45天;(3)设改进技术后,还要a天完成不少于6000台的生产计划,由题意,得2700+30a≥6000,解得:a≥110.答:改进技术后,至少还要110天完成不少于6000台的生产计划.
【考点】一元一次不等式的应用,一次函数的实际应用
【解析】【分析】(1)本题是一道分段函数,当0≤x≤90时和x>90时由待定系数法就可以分别求出其结论;
(2)由(1)的解析式求出今年前90天平均每天的生产数量,由函数图象可以求出去年的生产总量就可以得出结论;
(3)设改进技术后,至少还要a天完成不少于6000台的生产计划,根据前90天的生产量+改进技术后的生产量≥6000建立不等式求出其解即可.
(
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
(
第
1
页 共
3
页
)
一、单选题
1.下列四个备选项中,其中有一个选项的内容从表达形式上看不属于函数,则这一个选项是( )
A. y= B. y=3x+1 C. y=-2x +x-1 D.
2.当自变量x=3时,函数y=﹣x﹣3的函数值为( )
A. 0 B. 9 C. 6 D. ﹣6
3.函数y= 中,自变量x的取值范围是( )
A. x>2 B. x≠2 C. x>-1 D. x≠-1
4.下列函数中,是一次函数的是( )
A. B. C. y=5x2+x D. y= 8
5.下列图象不能表示函数关系的是( )
A. B. C. D.
6.函数 的自变量 的取值范围是( )
A. B. C. D. ,且
7.函数 的图象如图所示,则函数 的大致图象是( )
A. B. C. D.
8.某汽车从A开往360km外的B,全程的前一部分为高速公路,后一部分为普通公路.若汽车在高速公路和普通公路上分别以某一速度匀速行驶,汽车行驶的路程y(单位:km)与时间x(单位:h)之间的关系如图所示,则下列结论正确的是( )
A. 汽车在高速公路上的行驶速度为100km/h B. 普通公路总长为90km
C. 汽车在普通公路上的行驶速度为60km/h D. 汽车出发后4h到B地
9.已知:直线y= x+ (n为正整数)与两坐标轴围成的三角形面积为Sn , 则S1+S2+S3+…+S2019( )
A. B. C. D.
10.如图,等腰Rt△ABC中,BC= ,以边AC为斜边向右做等腰Rt△ACD,点E是线段CD的中点,连接 AE.作线段CE关于直线AC的对称线段CF,连接BF,并延长BF交线段AE于点G,则线段BG长为( )
A. B. C. D.
二、填空题
11.球的表面积S与半径R之间的关系是S=4πR2 . 对于各种不同大小的圆,请指出公式S=4πR2中常量是 ,变量是
12.在一次函数y=-2(x+1)+x中,一次项系数k为________,常数项b为________.
13.函数y= 自变量x的取值范围是________.
14.若函数y= 有意义,则自变量x的取值范围是 .
15.在函数y= 中,自变量x的取值范围是 .
16.小亮拿15元钱去文具店买签字笔,每支1.5元,小亮买签字笔后所剩钱数 (元)与买签字笔的支数 (支)之间的关系式为 .
17.函数y= 中,自变量x的取值范围是 .
18.已知: 、 、 是三个非负数,并且满足 , ,设 ,设 为 的最大值.则 的值为 .
三、解答题
19.已知函数 是一次函数,求m的值.
20.当k取何值时,关于x的方程2(2x-3)=1-2x和8-k=2(x+ )的解相同?
21.填表,并在同一坐标系内作出函数y=2x-5 和y=-x+1的图像;
填表:y=2x-5
x … 0 …
y … 0 …
y=-x+1
x … 0 …
y … 0 …
22.已知一次函数 中,y随x的增大而减小,且其图象与y轴交点在x轴上方.求m的取值范围.
23.已知弹簧的长度y(厘米)在一定的限度内是所挂物质量x(千克)的一次函数.现已测得不挂重物时弹簧的长度是6厘米,挂4千克质量的重物时,弹簧的长度是7. 2厘米,求这个一次函数的关系式.
24.已知两个变量x、y满足关系2x﹣3y+1=0,试问:①y是x的函数吗?②x是y的函数吗?若是,写出y与x的关系式,若不是,说明理由.
25.某校餐厅计划购买12张餐桌和一批餐椅,现从甲、乙两商场了解到:同一型号的餐桌报价每张均为200元,餐椅报价每把均为50元.甲商场称:每购买一张餐桌赠送一把餐椅;乙商场规定:所有餐桌椅均按报价的八五折销售.那么,学校应如何购买更优惠?
26.如图,直线y=﹣2x+6与直线y=mx+n相交于点M(p,4).
(1)求p的值;
(2)直接写出关于x,y的二元一次方程组的解;
(3)判断直线y=3nx+m﹣2n是否也过点M?并说明理由.
27.已知:y=(k-1)x|k|+k2-4是一次函数,求(3k+2)2007的值.
28.随着生活质量的提高,人们健康意识逐渐增强,安装净水设备的百姓家庭越来越多.某厂家从去年开始投入生产净水器,生产净水器的总量y(台)与今年的生产天数x(天)的关系如图所示.今年生产90天后,厂家改进了技术,平均每天的生产数量达到30台.
(1)求y与x之间的函数表达式;
(2)已知该厂家去年平均每天的生产数量与今年前90天平均每天的生产数量相同,求厂家去年生产的天数;
(3)如果厂家制定总量不少于6000台的生产计划,那么在改进技术后,至少还要多少天完成生产计划?
答案解析部分
一、单选题
1.【答案】 D
【考点】函数的概念
【解析】【解答】解:A、 , y是x的函数,故A不符合题意;
B、y=3x+1,y是x的一次函数,故B不符合题意;
C、 y=-2x +x-1,y是x的二次函数,故C不符合题意;
D、 , 这是关于x的分式方程,表示函数,故D符合题意;
故答案为:D.
【分析】利用函数的定义:一般地,在一个变化过程中,如果有两个变量x与y,并且对于x的每一个确定的值,y都有惟一确定的值与其对应,那么我们就说x是自变量,y是x的函数,再对各选项逐一判断。
2.【答案】 D
【考点】函数值
【解析】【解答】解:当x=3时,y=﹣1×3﹣3=﹣6.
故答案为:D.
【分析】代入x=3求出与之对应的y值,此题得解.
3.【答案】 D
【考点】函数自变量的取值范围
【解析】【解答】解:根据题意可得x+1≠0;
解得x≠-1;
故答案为:D.
【分析】这是一个自变量在分母的函数,须分母不为0,求出自变量的取值范围x≠-1。
4.【答案】 B
【考点】一次函数的定义
【解析】【解答】解: 是反比例函数,故A不符合题意;
是一次函数,也是正比例函数,故B符合题意;
y=5x2+x,是二次函数,故C不符合题意;
y= 8不是一次函数,故D不符合题意;
故答案为:B.
【分析】根据一次函数的定义逐项判定即可。
5.【答案】 A
【考点】函数的图象
【解析】【解答】解:如图所示,
作x轴的垂线,与图象有两个交点,所以y不是x的函数;
B、C、D作x轴的任意一条垂线,与图象均只有一个交点,所以B、C、D中y是x的函数.
故答案为:A.
【分析】根据函数里一个x值对应一个y值,可判断图像是否是函数。
6.【答案】 A
【考点】函数自变量的取值范围
【解析】【解答】解:函数 的自变量 的取值范围是: ,
故答案为:A.
【分析】观察含自变量的式子,含有分式,只需分母不等于0,可求出x的取值范围.
7.【答案】 B
【考点】一次函数图象、性质与系数的关系
【解析】【解答】解:由函数y=ax+b-2的图象可得:a<0,b-2=0,
∴a<0,b=2>0,
所以函数y=-ax-b的大致图象经过第一、四、三象限,
故答案为:B.
【分析】根据一次函数的图象的性质确定a和b的符号,进而解答即可.
8.【答案】 C
【考点】函数的图象
【解析】【解答】解:由题意可得,
汽车在高速公路上行驶速度为:180÷2=90km/h,故选项A错误,
普通公路的总长为:360﹣180=180km,故选项B错误,
汽车在普通公路上行驶的速度为:(270﹣180)÷(3.5﹣2)=60km/h,故选项C正确,
汽车出发后到达B地的时间为:2+(360﹣180)÷60=5h,故选项D错误,
故选C.
【分析】根据题意和图象可以分别计算出各个选项中的量,从而可以判断哪个选项是正确的,从而可以解答本题.
9.【答案】 D
【考点】一次函数的图象,三角形的面积
【解析】【解答】解:∵当n=1时,直线为y= x+ ,
∴直线与两坐标轴的交点为(0, ),(-1,0),
∴S1= ×1× = ;
当n=2时,直线为y= x+ ,
∴直线与两坐标轴的交点为(0, ),(- ,0),
∴S2= × × = × ;
当n=3时,直线为y= x+ ,
∴直线与两坐标轴的交点为(0, ),(- ,0),
∴S3= × × = × ;
…,
Sn= × ,
∴S1+S2+S3+…+S2019= ×(1- + + +…+ - )= (1- )=
故答案为:D.
【分析】依次求出S1、S2、S3 , 就发现规律:Sn= × ,然后求其和即可求得答案.注意 .
10.【答案】 B
【考点】点的坐标,一次函数的实际应用
【解析】【解答】解:建立如图所示坐标系,使BC与x轴重合,AC与y轴重合,
∵ ABC和 ACD都是等腰直角三角形,且BC= ,
∴AC=BC= ,AB= ,AD=CD= ,
可将各点坐标表示出来,A(0, ),B( ,0),C(0,0),D( , ),
∴点E为CD中点,故E的坐标为( , ),
又∵CF为CE关于AC的对称线段,故F的坐标为( , ),
设直线BF的解析式为:y=kx+b,将B点、F点坐标代入,
,解得: ,
∴直线BF的解析式为: ,
设直线AE的解析式为:y=mx+n,将A点、E点坐标代入,
,解得: ,
∴直线BF的解析式为: ,
直线BF与AE相交于点G,
,解得: ,即G( , ),
线段BG的长度为: ,
故答案为:B.
【分析】建立如下图所示坐标系,使BC与x轴重合,AC与y轴重合,可将各点坐标求出,并通过两点式分别求出直线BF、直线AE的解析式,直线BF与AE相交于点G,即可求出BG的长度.
二、填空题
11.【答案】 4π;S和R
【考点】常量、变量
【解析】【解答】解:公式S=4πR2中常量是4π,变量是S和R.
故答案是:4π;S和R.
【分析】变量是指在程序的运行过程中随时可以发生变化的量,常量是数值始终不变的量,根据定义即可确定.
12.【答案】 -1;-2
【考点】一次函数的定义
【解析】【解答】解:将 y=-2(x+1)+x 变形,得:y=-x-2 ,
则k=-1;b=-2
故答案为: -1;-2.
【分析】 将一次函数y=-2(x+1)+x展开合并同类项化为y=kx+b的形式,即可看出一次项系数k和常数项b 的值.
13.【答案】 x≠4
【考点】函数自变量的取值范围
【解析】【解答】解:由题意得:4-x≠0,
∴x≠4.
故答案为:x≠4.
【分析】分式有意义的条件是分母不等于0,据此列不等式求出x的范围即可.
14.【答案】 x≠
【考点】函数自变量的取值范围
【解析】【解答】解:根据题意得:4x+1≠0,解得:x≠ .
故答案为:x≠ .
【分析】本题要求分母不能为0,因为当分母为0时,函数没有意义;
15.【答案】 x≠﹣1
【考点】函数自变量的取值范围
【解析】【解答】解:由题意,得
x+1≠0,
解得x≠﹣1,
故答案为:x≠﹣1.
【分析】分式有意义的条件为分母不为0.
16.【答案】 y=15-1.5x
【考点】根据实际问题列一次函数表达式
【解析】【解答】解:买签字笔的支数x(支)花的钱数是1.5x元,则剩余的钱数是(15-1.5x)元,
则签字笔后所剩钱数 (元)与买签字笔的支数 (支)之间的关系式为y=15-1.5x.
故答案为:y=15-1.5x.
【分析】根据小亮拿15元钱去文具店买签字笔,每支1.5元,进行求解即可。
17.【答案】 x≠﹣3
【考点】函数自变量的取值范围
【解析】【解答】解:由题意得,x+3≠0,
解得x≠﹣3.
故答案为:x≠﹣3.
【分析】根据分母不等于0列式计算即可得解.
18.【答案】
【考点】三元一次方程组解法及应用,一次函数的性质
【解析】【解答】解:3a+2b+c=6,2a+b-3c=1,
解得a=7c-4,b=9-11c;
∵a≥0、b≥0,
∴7c-4≥0,9-11c≥0,
∴ .
∵m=3a+b-7c=3c-3,
∴m随c的增大而增大,
∵ .
∴当c取最大值 ,m有最大值,
∴m的最大值为s=3× -3= .
故答案为: .
【分析】根据题意先把c看作已知数,分别用c表示出a和b ,让a≥0,b≥0 列式求出c的取值范围,再求得m用c表示的形式,结合c的取值范围即可求得s的值.
三、解答题
19.【答案】 解:∵函数 是一次函数,
∴m+2≠0且m2-3=1,
解得:m=2,
【考点】一次函数的定义
【解析】【分析】一次函数要求自变量x前的系数不等于0,指数是1,据此即可解题.
20.【答案】 解方程2(2x-3)=1-2x,得x= .把x= 代入8-k=2(x+ ),得8-k=4,即k=4.
【考点】一次函数与一元一次方程的综合应用
【解析】【分析】根据解方程,可得方程的解,根据方程的解相同,可得关于k的一元一次方程,根据解方程,可得答案.
21.【答案】 解:当x=0时,y=2×0-5=-5,当y=0时,0=2x-5,x=2.5;当x=0代入y=0+1=1,当y=0时,0=-x+1,x=1。填表如下:
x … 0 2.5 …
y … -5 0 …
x … 0 1 …
y … 1 0 …
过点(0,-5),(2.5,0)画直线,可得函数y=2x-5的图象;过点(0,1),(1,0)画直线,可得函数y=-x+1的图象。如下图:
【考点】一次函数的图象
【解析】【分析】本题考查了一次函数的图象性质,一次函数图象上点的坐标特征及图象的画法,是基础知识,需熟练掌握。
22.【答案】 解:∵一次函数y随x的增大而减小∴ 又∵其图象与y轴交点在x轴上方m+1>0 ∴m的取值范围是:
【考点】一次函数的性质
【解析】【分析】一次函数中,y随x增大而减小,说明自变量系数小于0,即2m-2<0,图象过二、四象限;又该函数的图象与y轴交点在x轴上方,据此解答m的取值范围即
23.【答案】 设所求函数的关系式是y=kx+b,
根据题意,得
解这个方程组,得
所以所求函数的关系式是y=0.3x+6
【考点】根据实际问题列一次函数表达式
【解析】【分析】已知所求函数为一次函数,可以设所求函数的关系式是y=kx+b,再由题中的已知条件代入上式,求出k、b的值,代入y=kx+b,即可求的这个一次函数的关系式.
24.【答案】 解:根据题意可知:①y= ,∵对于x的每一个取值,y都有唯一确定的值,
∴y是x的函数;
②x= ,∵对于y的每一个取值,x都有唯一确定的值,
∴x是y的函数
【考点】函数的概念,函数解析式
【解析】【分析】根据函数的定义可知,满足对于x的每一个取值,y都有唯一确定的值与之对应关系,据此即可得出答案.
25.【答案】 解:设学校购买12张餐桌和 把餐椅,到购买甲商场的费用为 元,到乙商场购买的费用为 元,则有
当 ,即 时,
答:当学校购买的餐椅少于32把时,到甲商场购买更优惠。
【考点】一次函数的实际应用,根据实际问题列一次函数表达式
【解析】【分析】 设学校购买12张餐桌和 把餐椅,到购买甲商场的费用为 元,到乙商场购买的费用为 元,根据购买的费用=购买桌子的数量×桌的单价+购买椅子的数量×椅子的单价,分别表示出y1与y2的关系式;分三种情况①当y1>y2,②y1=y2,③y1<y2时讨论即得.
26.【答案】 解:(1)∵直线y=﹣2x+6经过点M(p,4),
∴4=﹣2p+6,
∴p=1.
(2)由图象可知方程组的解为 ,
(3)结论:直线y=3nx+m﹣2n经过点M,理由如下:
∵点M(1,4)在直线y=mx+n上,
∴m+n=4,
∴当x=1,时,y=3nx+m﹣2n=m+n=4,
∴直线y=3nx+m﹣2n经过点M.
【考点】一次函数与二元一次方程(组)的综合应用
【解析】【分析】(1)根据直线y=﹣2x+6经过点M,即可求出p.
(2)由图象可知交点的坐标就是方程组的解.
(3)先求出m+n=4,用代入法可以解决.
27.【答案】 解答:由题意得:|k|=1且k-1≠0,解得:k=-1,(3k+2)2007=(-3+2)2007=-1
【考点】一次函数的定义
【解析】【分析】首先根据一次函数定义确定k的值,再代入代数式(3k+2)2007求值.
28.【答案】 解:(1)当0≤x≤90时,设y与x之间的函数关系式为y=kx+b,由函数图象,得 , 解得: . 则y=20x+900.当x>90时,由题意,得y=30x.∴y=;(2)由题意,得∵x=0时,y=900,∴去年的生产总量为900台.今年平均每天的生产量为:(2700﹣900)÷90=20台,厂家去年生产的天数为:900÷20=45天.答:厂家去年生产的天数为45天;(3)设改进技术后,还要a天完成不少于6000台的生产计划,由题意,得2700+30a≥6000,解得:a≥110.答:改进技术后,至少还要110天完成不少于6000台的生产计划.
【考点】一元一次不等式的应用,一次函数的实际应用
【解析】【分析】(1)本题是一道分段函数,当0≤x≤90时和x>90时由待定系数法就可以分别求出其结论;
(2)由(1)的解析式求出今年前90天平均每天的生产数量,由函数图象可以求出去年的生产总量就可以得出结论;
(3)设改进技术后,至少还要a天完成不少于6000台的生产计划,根据前90天的生产量+改进技术后的生产量≥6000建立不等式求出其解即可.
(
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
(
第
1
页 共
3
页
)
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
