人教版八年级上册12.3角的平分线的性质(1)教案(表格式)
文档属性
| 名称 | 人教版八年级上册12.3角的平分线的性质(1)教案(表格式) |
|
|
| 格式 | doc | ||
| 文件大小 | 174.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-04 21:30:46 | ||
图片预览

文档简介
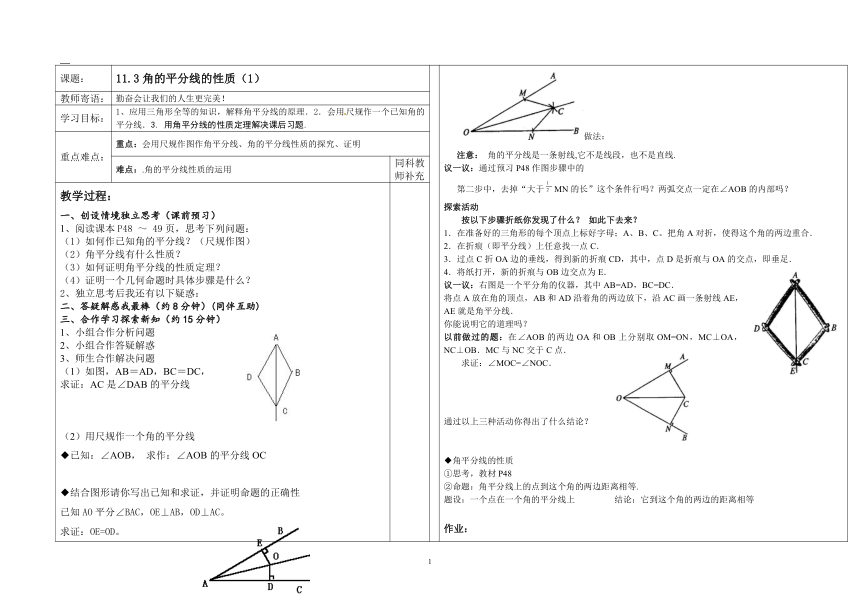
课题: 11.3角的平分线的性质(1) 做法: 注意: 角的平分线是一条射线,它不是线段,也不是直线.议一议:通过预习P48作图步骤中的 第二步中,去掉“大于MN的长”这个条件行吗?两弧交点一定在∠AOB的内部吗?探索活动 按以下步骤折纸你发现了什么? 如此下去来?1.在准备好的三角形的每个顶点上标好字母;A、B、C。把角A对折,使得这个角的两边重合.2.在折痕(即平分线)上任意找一点C.3.过点C折OA边的垂线,得到新的折痕CD,其中,点D是折痕与OA的交点,即垂足.4.将纸打开,新的折痕与OB边交点为E.议一议:右图是一个平分角的仪器,其中AB=AD,BC=DC.将点A放在角的顶点,AB和AD沿着角的两边放下,沿AC画一条射线AE,AE就是角平分线.你能说明它的道理吗?以前做过的题:在∠AOB的两边OA和OB上分别取OM=ON,MC⊥OA,NC⊥OB.MC与NC交于C点. 求证:∠MOC=∠NOC. 通过以上三种活动你得出了什么结论?◆角平分线的性质①思考,教材P48②命题:角平分线上的点到这个角的两边距离相等.题设:一个点在一个角的平分线上 结论:它到这个角的两边的距离相等作业:独立完成( ) 求助后独立完成( )未及时完成( ) 未完成( )八、课后反思:1、学习目标完成情况反思:2、掌握重点突破难点情况反思:3、错题记录及原因分析:附加题:1、如图:在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,BD=DF; 求证:CF=EB2、在Rt△ABC中,BD平分∠ABC, DE⊥AB于E,则⑴图中相等的线段有哪些?相等的角呢?⑵哪条线段与DE相等?为什么?⑶若AB=10,BC=8,AC=6,求BE,AE的长和△AED的周长。
教师寄语: 勤奋会让我们的人生更完美!
学习目标: 1、应用三角形全等的知识,解释角平分线的原理.2.会用尺规作一个已知角的平分线.3. 用角平分线的性质定理解决课后习题.
重点难点: 重点:会用尺规作图作角平分线、角的平分线性质的探究、证明
难点:.角的平分线性质的运用 同科教师补充
教学过程:一、创设情境独立思考(课前预习)1、阅读课本P48 ~ 49页,思考下列问题:(1)如何作已知角的平分线?(尺规作图)(2)角平分线有什么性质?(3)如何证明角平分线的性质定理?(4)证明一个几何命题时具体步骤是什么?2、独立思考后我还有以下疑惑:二、答疑解惑我最棒(约8分钟)(同伴互助)三、合作学习探索新知(约15分钟)1、小组合作分析问题2、小组合作答疑解惑3、师生合作解决问题(1)如图,AB=AD,BC=DC,求证:AC是∠DAB的平分线(2)用尺规作一个角的平分线◆已知:∠AOB, 求作:∠AOB的平分线OC◆结合图形请你写出已知和求证,并证明命题的正确性已知AO平分∠BAC,OE⊥AB,OD⊥AC。求证:OE=OD。四、归纳总结巩固新知(约15分钟)1、知识点的归纳总结:(1)角平分线上的 到角两边的 相等。(2)证明命题的步骤:①画图②已知,求证③证明2、运用新知解决问题:(重点例习题的强化训练)(1)、课本P49页思考(2)、课本P50页练习第1题五、课堂小测(约5分钟)如图所示OC是∠AOB 的平分线,P 是OC上任意一点,问PE=PD 为什么 六、独立作业我能行课本P51页习题12.3第2、4两题。 七、自我评价课上1、本节课我对自己最满意的一件事是:2、本节课我对自己最不满意的一件事是:
E
D
C
B
A
O
A
B
E
D
C
P
PAGE
1
教师寄语: 勤奋会让我们的人生更完美!
学习目标: 1、应用三角形全等的知识,解释角平分线的原理.2.会用尺规作一个已知角的平分线.3. 用角平分线的性质定理解决课后习题.
重点难点: 重点:会用尺规作图作角平分线、角的平分线性质的探究、证明
难点:.角的平分线性质的运用 同科教师补充
教学过程:一、创设情境独立思考(课前预习)1、阅读课本P48 ~ 49页,思考下列问题:(1)如何作已知角的平分线?(尺规作图)(2)角平分线有什么性质?(3)如何证明角平分线的性质定理?(4)证明一个几何命题时具体步骤是什么?2、独立思考后我还有以下疑惑:二、答疑解惑我最棒(约8分钟)(同伴互助)三、合作学习探索新知(约15分钟)1、小组合作分析问题2、小组合作答疑解惑3、师生合作解决问题(1)如图,AB=AD,BC=DC,求证:AC是∠DAB的平分线(2)用尺规作一个角的平分线◆已知:∠AOB, 求作:∠AOB的平分线OC◆结合图形请你写出已知和求证,并证明命题的正确性已知AO平分∠BAC,OE⊥AB,OD⊥AC。求证:OE=OD。四、归纳总结巩固新知(约15分钟)1、知识点的归纳总结:(1)角平分线上的 到角两边的 相等。(2)证明命题的步骤:①画图②已知,求证③证明2、运用新知解决问题:(重点例习题的强化训练)(1)、课本P49页思考(2)、课本P50页练习第1题五、课堂小测(约5分钟)如图所示OC是∠AOB 的平分线,P 是OC上任意一点,问PE=PD 为什么 六、独立作业我能行课本P51页习题12.3第2、4两题。 七、自我评价课上1、本节课我对自己最满意的一件事是:2、本节课我对自己最不满意的一件事是:
E
D
C
B
A
O
A
B
E
D
C
P
PAGE
1
