人教版数学八年级上册第十一章 三角11.1 与三角形有关的线段—线段差的最大值问题教案
文档属性
| 名称 | 人教版数学八年级上册第十一章 三角11.1 与三角形有关的线段—线段差的最大值问题教案 |
|
|
| 格式 | doc | ||
| 文件大小 | 128.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-05 09:52:19 | ||
图片预览

文档简介
线段差的最大值问题教案
教学目的:
知识和技能:让学生掌握线段差的最大值问题的解决模型。
过程与方法:利用轴对称化“折”为“直”,通过类比让学生找到解决问题的途径和方法,建立数学模型。
情感态度与价值观:培养团结协作能力,提高对数学的兴趣。
教学重点:通过类比转化建立最值模型
教学难点:最值模型的灵活应用
教学过程:
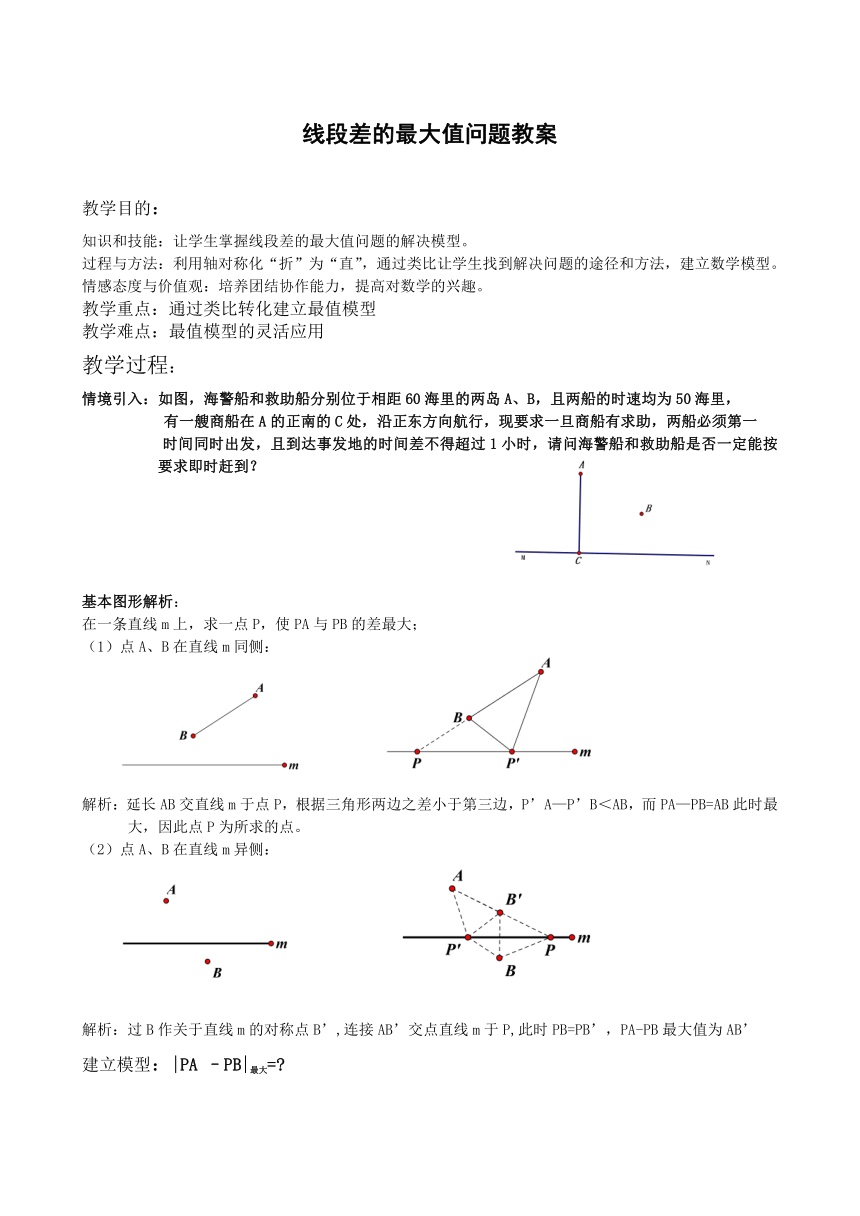
情境引入:如图,海警船和救助船分别位于相距60海里的两岛A、B,且两船的时速均为50海里,
有一艘商船在A的正南的C处,沿正东方向航行,现要求一旦商船有求助,两船必须第一
时间同时出发,且到达事发地的时间差不得超过1小时,请问海警船和救助船是否一定能按要求即时赶到?
基本图形解析:
在一条直线m上,求一点P,使PA与PB的差最大;
(1)点A、B在直线m同侧:
解析:延长AB交直线m于点P,根据三角形两边之差小于第三边,P’A—P’B<AB,而PA—PB=AB此时最大,因此点P为所求的点。
(2)点A、B在直线m异侧:
解析:过B作关于直线m的对称点B’,连接AB’交点直线m于P,此时PB=PB’,PA-PB最大值为AB’
建立模型:|PA –PB|最大=
|PA –PB|最大=AB
理论依据:
三角形两边之和大于第三边,两边之差小于第三边
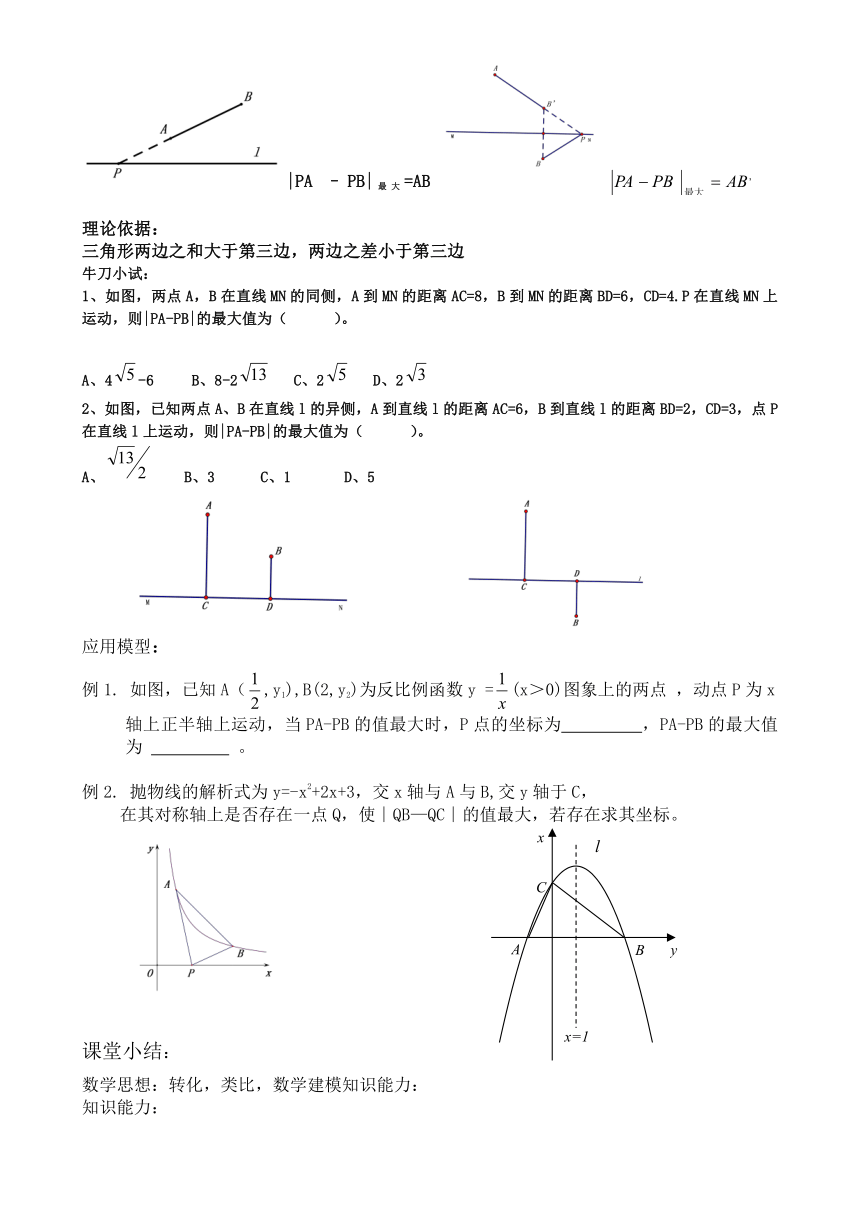
牛刀小试:
1、如图,两点A,B在直线MN的同侧,A到MN的距离AC=8,B到MN的距离BD=6,CD=4.P在直线MN上运动,则|PA-PB|的最大值为( )。
A、4-6 B、8-2 C、2 D、2
2、如图,已知两点A、B在直线l的异侧,A到直线l的距离AC=6,B到直线l的距离BD=2,CD=3,点P在直线l上运动,则|PA-PB|的最大值为( )。
A、 B、3 C、1 D、5
应用模型:
例1. 如图,已知A(,y1),B(2,y2)为反比例函数y =(x>0)图象上的两点 ,动点P为x轴上正半轴上运动,当PA-PB的值最大时,P点的坐标为 ,PA-PB的最大值为 。
例2. 抛物线的解析式为y=-x2+2x+3,交x轴与A与B,交y轴于C,
在其对称轴上是否存在一点Q,使∣QB—QC∣的值最大,若存在求其坐标。
课堂小结:
数学思想:转化,类比,数学建模知识能力:
知识能力:
|PA –PB|最大=AB
方法归纳:利用轴对称化“折”为“直”,将两条线段转化在同一直线上,即“共线”,使所求差用一条线段表示。
巩固练习:
1、如图,正方形ABCD的边长为a,M为AB的中点,CN=CD,点P在直线AC上,则|PM-PN|最大值为 。
2. 如图,抛物线y=-x 2-x+2的顶点为A,与y 轴交于点B.
(1)求点A、点B的坐标;
(2)当PA-PB最大时,求点P的坐标.
3. 如图,反比例函数y =k/x (x>0)图象上的两点 A、B的横坐标为1,3,点P为x轴上正半轴上一
点,若PA-PB的最大值为2 ,则k= 。
4.如图,已知直线y=x+1与y轴交于点A,与x轴交于点D,
抛物线y=x 2+bx+c与直线交于A、E两点,与x轴交于B、C两点,且B点坐标为(1,0).
(1)求该抛物线的解析式;
(2)在抛物线的对称轴上找一点M,使|AM-MC|的值最大,求出点M的坐标.
提高题:
如图,直线y=-x+2与x轴交于点C,与y轴交于点B,点A为y轴正半轴上的一点,⊙A经过点B和点O,直线BC交⊙A于点D.
(1)求点D的坐标;
(2)过O,C,D三点作抛物线,在抛物线的对称轴上是否存在一点P,使线段PO与PD之差的值最大?若存在,请求出这个最大值和点P的坐标.若不存在,请说明理由.
y
C
x
B
A
x=1
y
x
C
B
A
D
O
E
y
教学目的:
知识和技能:让学生掌握线段差的最大值问题的解决模型。
过程与方法:利用轴对称化“折”为“直”,通过类比让学生找到解决问题的途径和方法,建立数学模型。
情感态度与价值观:培养团结协作能力,提高对数学的兴趣。
教学重点:通过类比转化建立最值模型
教学难点:最值模型的灵活应用
教学过程:
情境引入:如图,海警船和救助船分别位于相距60海里的两岛A、B,且两船的时速均为50海里,
有一艘商船在A的正南的C处,沿正东方向航行,现要求一旦商船有求助,两船必须第一
时间同时出发,且到达事发地的时间差不得超过1小时,请问海警船和救助船是否一定能按要求即时赶到?
基本图形解析:
在一条直线m上,求一点P,使PA与PB的差最大;
(1)点A、B在直线m同侧:
解析:延长AB交直线m于点P,根据三角形两边之差小于第三边,P’A—P’B<AB,而PA—PB=AB此时最大,因此点P为所求的点。
(2)点A、B在直线m异侧:
解析:过B作关于直线m的对称点B’,连接AB’交点直线m于P,此时PB=PB’,PA-PB最大值为AB’
建立模型:|PA –PB|最大=
|PA –PB|最大=AB
理论依据:
三角形两边之和大于第三边,两边之差小于第三边
牛刀小试:
1、如图,两点A,B在直线MN的同侧,A到MN的距离AC=8,B到MN的距离BD=6,CD=4.P在直线MN上运动,则|PA-PB|的最大值为( )。
A、4-6 B、8-2 C、2 D、2
2、如图,已知两点A、B在直线l的异侧,A到直线l的距离AC=6,B到直线l的距离BD=2,CD=3,点P在直线l上运动,则|PA-PB|的最大值为( )。
A、 B、3 C、1 D、5
应用模型:
例1. 如图,已知A(,y1),B(2,y2)为反比例函数y =(x>0)图象上的两点 ,动点P为x轴上正半轴上运动,当PA-PB的值最大时,P点的坐标为 ,PA-PB的最大值为 。
例2. 抛物线的解析式为y=-x2+2x+3,交x轴与A与B,交y轴于C,
在其对称轴上是否存在一点Q,使∣QB—QC∣的值最大,若存在求其坐标。
课堂小结:
数学思想:转化,类比,数学建模知识能力:
知识能力:
|PA –PB|最大=AB
方法归纳:利用轴对称化“折”为“直”,将两条线段转化在同一直线上,即“共线”,使所求差用一条线段表示。
巩固练习:
1、如图,正方形ABCD的边长为a,M为AB的中点,CN=CD,点P在直线AC上,则|PM-PN|最大值为 。
2. 如图,抛物线y=-x 2-x+2的顶点为A,与y 轴交于点B.
(1)求点A、点B的坐标;
(2)当PA-PB最大时,求点P的坐标.
3. 如图,反比例函数y =k/x (x>0)图象上的两点 A、B的横坐标为1,3,点P为x轴上正半轴上一
点,若PA-PB的最大值为2 ,则k= 。
4.如图,已知直线y=x+1与y轴交于点A,与x轴交于点D,
抛物线y=x 2+bx+c与直线交于A、E两点,与x轴交于B、C两点,且B点坐标为(1,0).
(1)求该抛物线的解析式;
(2)在抛物线的对称轴上找一点M,使|AM-MC|的值最大,求出点M的坐标.
提高题:
如图,直线y=-x+2与x轴交于点C,与y轴交于点B,点A为y轴正半轴上的一点,⊙A经过点B和点O,直线BC交⊙A于点D.
(1)求点D的坐标;
(2)过O,C,D三点作抛物线,在抛物线的对称轴上是否存在一点P,使线段PO与PD之差的值最大?若存在,请求出这个最大值和点P的坐标.若不存在,请说明理由.
y
C
x
B
A
x=1
y
x
C
B
A
D
O
E
y
