八年级数学三角形全等判定1
图片预览




文档简介
(共14张PPT)
11.2 三角形全 等的判定(一)
A
B
C
D
E
F
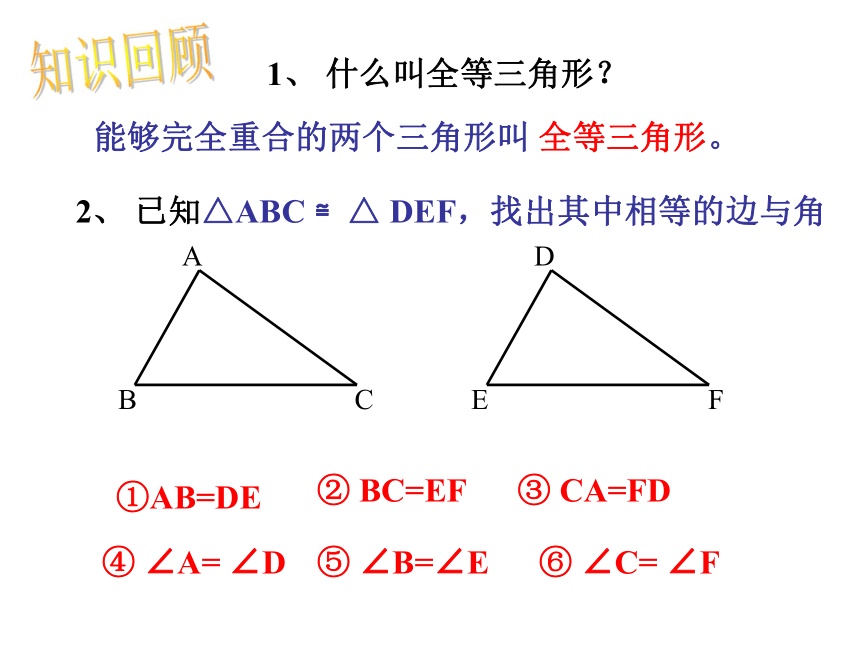
1、 什么叫全等三角形?
能够完全重合的两个三角形叫 全等三角形。
2、 已知△ABC ≌△ DEF,找出其中相等的边与角
①AB=DE
③ CA=FD
② BC=EF
④ ∠A= ∠D
⑤ ∠B=∠E
⑥ ∠C= ∠F
A
B
C
A′
B′
C′
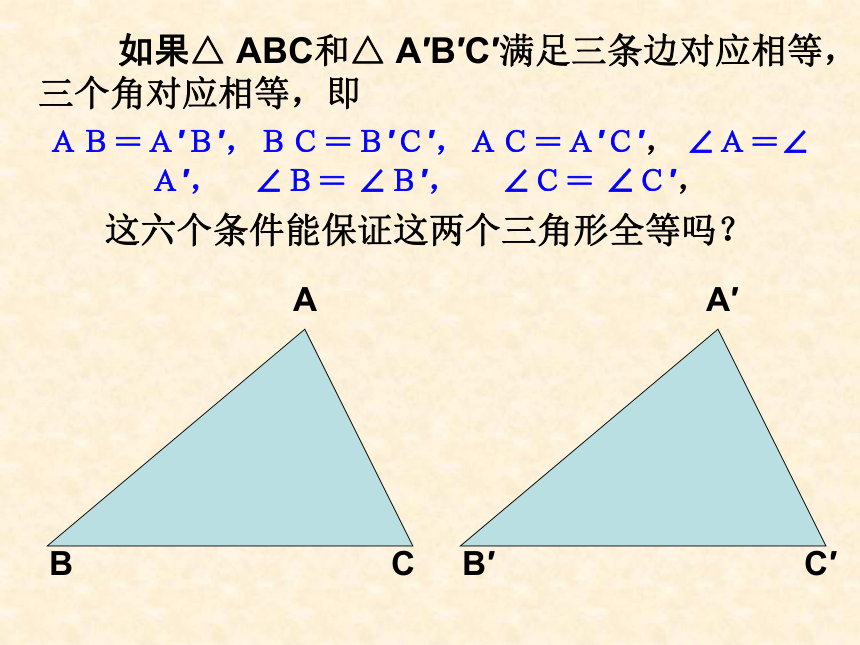
如果△ ABC和△ A′B′C′满足三条边对应相等,三个角对应相等,即
AB=A′B′,BC=B′C′,AC=A′C′, ∠A=∠A′, ∠B= ∠B′, ∠C= ∠C′,
这六个条件能保证这两个三角形全等吗?
1.一条边对应相等时;
如果只给一个条件:
2.一个角对应相等时;
结论:只有一条边或一个角对应相等的两个三角形 不一定全等.
如果给出两个条件画三角形,
你能说出有哪几种可能的情况?
①两边;
③一边一角。
②两角;
结论:满足两个条件时两个三角形不一定全等.
如果给出三个条件画三角形,
你能说出有哪几种可能的情况?
①三边;
②三角;
③两边一角;
④两角一边。
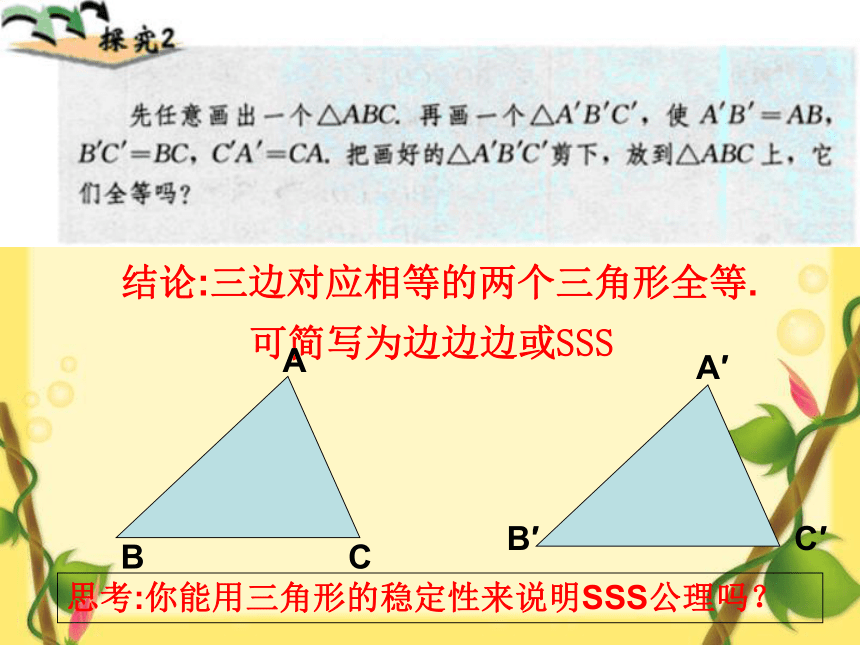
结论:三边对应相等的两个三角形全等.
可简写为边边边或SSS
思考:你能用三角形的稳定性来说明SSS公理吗?
A
B
C
C′
B′
A′
A
B
C
D
E
F
〃
〃
\
\
≡
≡
在△ABC和△DEF中,
一定要记住这种全等证明的书写格式哟!
△ABC≌△DEF
∴
(SSS)
数学语言:
判断两个三角形全等的推理过程,叫做证明三角形全等。
证明:∵D是BC的中点(已知)
∴BD=CD
在△ABD与△ACD中
AB=AC(已知)
BD=CD(已证)
AD=AD(公共边)
∴△ABD≌△ACD(SSS)
A
B
C
D
间接条件转化直接条件
指明三角形
列齐条件
得出结论
例1如图, △ABC是一个钢架,AB=AC,AD是连接A与BC中点D的支架,求证: △ABD≌△ACD
BC=DC ( )
练习:已知:如图,AB=AD,BC=DC,
求证: ∠B =∠D
A
B
C
D
∴ △ABC △ADC(SSS)
≌
AB=AD ( )
证明:在△ABC和△ADC中
AC
AC ( )
=
已知
已知
公共边
∴∠B =∠D(全等三角形的对应角相等)
如图四边形ABCD中,AB=CD,AD=BC,你能把四边形ABCD分成两个相互全等的三角形吗 你有几种方法 你能证明你的方法吗 试一试.
证法一:连接BD
∵ AB=CD
AD=BC
BD=BD(公共边)
∴ △ABD ≌ △BCD﹙SSS﹚
{
证法二:连接AC
∵ AB=CD
AD=BC
AC=AC(公共边)
∴ △ABC ≌ △ACD ﹙SSS﹚
{
探研时空
在△ABD 和△BCD中
在△ABD 和△BCD中
你有什么收获?
作业:必做题:
11.2第 1. 2 题
选做题:如图,D、F是线段BC上的两点,
AB=CE,AF=DE,要使△ABF≌△ECD ,还需要什么条件?
B D F C
E
A
再见
11.2 三角形全 等的判定(一)
A
B
C
D
E
F
1、 什么叫全等三角形?
能够完全重合的两个三角形叫 全等三角形。
2、 已知△ABC ≌△ DEF,找出其中相等的边与角
①AB=DE
③ CA=FD
② BC=EF
④ ∠A= ∠D
⑤ ∠B=∠E
⑥ ∠C= ∠F
A
B
C
A′
B′
C′
如果△ ABC和△ A′B′C′满足三条边对应相等,三个角对应相等,即
AB=A′B′,BC=B′C′,AC=A′C′, ∠A=∠A′, ∠B= ∠B′, ∠C= ∠C′,
这六个条件能保证这两个三角形全等吗?
1.一条边对应相等时;
如果只给一个条件:
2.一个角对应相等时;
结论:只有一条边或一个角对应相等的两个三角形 不一定全等.
如果给出两个条件画三角形,
你能说出有哪几种可能的情况?
①两边;
③一边一角。
②两角;
结论:满足两个条件时两个三角形不一定全等.
如果给出三个条件画三角形,
你能说出有哪几种可能的情况?
①三边;
②三角;
③两边一角;
④两角一边。
结论:三边对应相等的两个三角形全等.
可简写为边边边或SSS
思考:你能用三角形的稳定性来说明SSS公理吗?
A
B
C
C′
B′
A′
A
B
C
D
E
F
〃
〃
\
\
≡
≡
在△ABC和△DEF中,
一定要记住这种全等证明的书写格式哟!
△ABC≌△DEF
∴
(SSS)
数学语言:
判断两个三角形全等的推理过程,叫做证明三角形全等。
证明:∵D是BC的中点(已知)
∴BD=CD
在△ABD与△ACD中
AB=AC(已知)
BD=CD(已证)
AD=AD(公共边)
∴△ABD≌△ACD(SSS)
A
B
C
D
间接条件转化直接条件
指明三角形
列齐条件
得出结论
例1如图, △ABC是一个钢架,AB=AC,AD是连接A与BC中点D的支架,求证: △ABD≌△ACD
BC=DC ( )
练习:已知:如图,AB=AD,BC=DC,
求证: ∠B =∠D
A
B
C
D
∴ △ABC △ADC(SSS)
≌
AB=AD ( )
证明:在△ABC和△ADC中
AC
AC ( )
=
已知
已知
公共边
∴∠B =∠D(全等三角形的对应角相等)
如图四边形ABCD中,AB=CD,AD=BC,你能把四边形ABCD分成两个相互全等的三角形吗 你有几种方法 你能证明你的方法吗 试一试.
证法一:连接BD
∵ AB=CD
AD=BC
BD=BD(公共边)
∴ △ABD ≌ △BCD﹙SSS﹚
{
证法二:连接AC
∵ AB=CD
AD=BC
AC=AC(公共边)
∴ △ABC ≌ △ACD ﹙SSS﹚
{
探研时空
在△ABD 和△BCD中
在△ABD 和△BCD中
你有什么收获?
作业:必做题:
11.2第 1. 2 题
选做题:如图,D、F是线段BC上的两点,
AB=CE,AF=DE,要使△ABF≌△ECD ,还需要什么条件?
B D F C
E
A
再见
