八年级数学19.1.2 平行四边形的判定(一)教案
文档属性
| 名称 | 八年级数学19.1.2 平行四边形的判定(一)教案 | 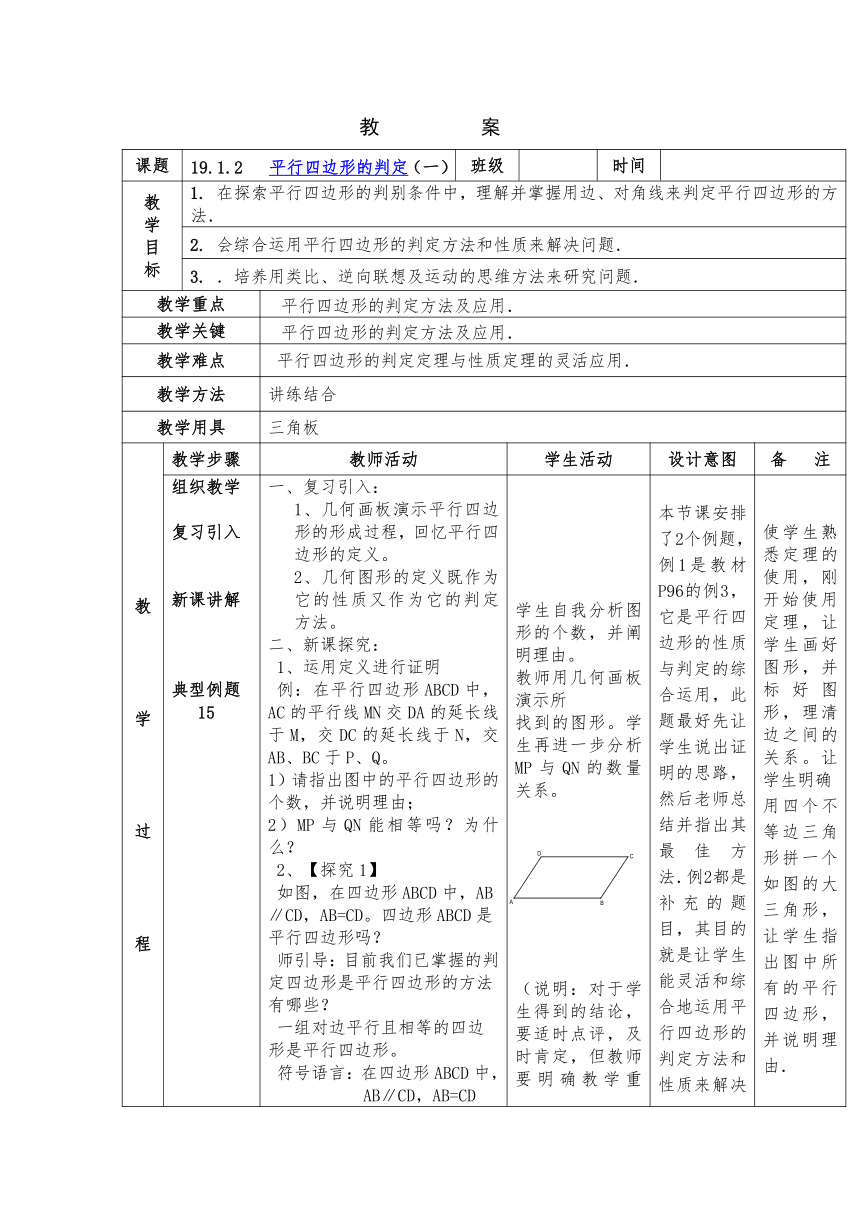 | |
| 格式 | zip | ||
| 文件大小 | 20.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-10-15 07:30:00 | ||
图片预览

文档简介
教 案
课题 19.1.2 平行四边形的判定 ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )(一) 班级 时间
教学目标 1. 在探索平行四边形的判别条件中,理解并掌握用边、对角线来判定平行四边形的方法.
2. 会综合运用平行四边形的判定方法和性质来解决问题.
3. .培养用类比、逆向联想及运动的思维方法来研究问题.
教学重点 平行四边形的判定方法及应用.
教学关键 平行四边形的判定方法及应用.
教学难点 平行四边形的判定定理与性质定理的灵活应用.
教学方法 讲练结合
教学用具 三角板
教学过程 教学步骤 教师活动 学生活动 设计意图 备 注
组织教学复习引入新课讲解典型例题 15定理应用:巩固提升归纳小结: 一、复习引入:1、几何画板演示平行四边形的形成过程,回忆平行四边形的定义。2、几何图形的定义既作为它的性质又作为它的判定方法。二、新课探究: 1、运用定义进行证明 例:在平行四边形ABCD中,AC的平行线MN交DA的延长线于M,交DC的延长线于N,交AB、BC于P、Q。1)请指出图中的平行四边形的个数,并说明理由;2)MP与QN能相等吗?为什么? 2、【探究1】 如图,在四边形ABCD中,AB∥CD,AB=CD。四边形ABCD是平行四边形吗? 师引导:目前我们已掌握的判定四边形是平行四边形的方法有哪些?一组对边平行且相等的四边形是平行四边形。符号语言:在四边形ABCD中, AB∥CD,AB=CD ∴四边形是ABCD平行四边形(一组对边平行且相等的四边形是平行四边形)例2:在ABCD中,E、F分别为CD、AB上的点,DE=BF。求证:四边形AFCE是平行四边形. 变式练习:1)将条件DE=BF更改为E、F分别为AB、CD的中点2)将条件DE=BF更改为∠DAB的平分线交CD于E,∠CBA的平分线交AB于F学生独立分析,比较这几个条件的联系与区别。1、已知,如图,在ABCD中,CN=AM,AE=CF求证:四边形MENF是平行四边形。1、已知,如图,在ABCD中,CN=AM,AE=CF求证:四边形MENF是平行四边形。1、知识方面:1)两组对边分别平行的四边形是平行四边形;2)一组对边平行且相等的四边形是平行四边形 3)两组对边分别相等的四边形是平行四边形2.思想方法方面:结合图形灵活选用判定方法 学生自我分析图形的个数,并阐明理由。教师用几何画板演示所找到的图形。学生再进一步分析MP与QN的数量关系。(说明:对于学生得到的结论,要适时点评,及时肯定,但教师要明确教学重点,进行取舍)分析:欲证四边形BFDE是平行四边形可以根据判定定理来证明.学生结合图形探究 。通过问题串的精心设计,引导学生对判定方法有深入的探究。 本节课安排了2个例题,例1是教材P96的例3,它是平行四边形的性质与判定的综合运用,此题最好先让学生说出证明的思路,然后老师总结并指出其最佳方法.例2都是补充的题目,其目的就是让学生能灵活和综合地运用平行四边形的判定方法和性质来解决问题.可以提高学生的动手能力和学生的思维能力,又可以提高学生的学习兴趣.本节课我们对平行四边形的判定进行了探究。通过这节课的学习,你有什么收获? 使学生熟悉定理的使用,刚开始使用定理,让学生画好图形,并标好图形,理清边之间的关系。让学生明确用四个不等边三角形拼一个如图的大三角形,让学生指出图中所有的平行四边形,并说明理由.引导学生自己小结本节课的知识要点及数学方法。
板书设计 19.1.2 平行四边形的判定 ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )(一)
例1 例2 练习 2
教学反思
课题 19.1.2 平行四边形的判定 ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )(一) 班级 时间
教学目标 1. 在探索平行四边形的判别条件中,理解并掌握用边、对角线来判定平行四边形的方法.
2. 会综合运用平行四边形的判定方法和性质来解决问题.
3. .培养用类比、逆向联想及运动的思维方法来研究问题.
教学重点 平行四边形的判定方法及应用.
教学关键 平行四边形的判定方法及应用.
教学难点 平行四边形的判定定理与性质定理的灵活应用.
教学方法 讲练结合
教学用具 三角板
教学过程 教学步骤 教师活动 学生活动 设计意图 备 注
组织教学复习引入新课讲解典型例题 15定理应用:巩固提升归纳小结: 一、复习引入:1、几何画板演示平行四边形的形成过程,回忆平行四边形的定义。2、几何图形的定义既作为它的性质又作为它的判定方法。二、新课探究: 1、运用定义进行证明 例:在平行四边形ABCD中,AC的平行线MN交DA的延长线于M,交DC的延长线于N,交AB、BC于P、Q。1)请指出图中的平行四边形的个数,并说明理由;2)MP与QN能相等吗?为什么? 2、【探究1】 如图,在四边形ABCD中,AB∥CD,AB=CD。四边形ABCD是平行四边形吗? 师引导:目前我们已掌握的判定四边形是平行四边形的方法有哪些?一组对边平行且相等的四边形是平行四边形。符号语言:在四边形ABCD中, AB∥CD,AB=CD ∴四边形是ABCD平行四边形(一组对边平行且相等的四边形是平行四边形)例2:在ABCD中,E、F分别为CD、AB上的点,DE=BF。求证:四边形AFCE是平行四边形. 变式练习:1)将条件DE=BF更改为E、F分别为AB、CD的中点2)将条件DE=BF更改为∠DAB的平分线交CD于E,∠CBA的平分线交AB于F学生独立分析,比较这几个条件的联系与区别。1、已知,如图,在ABCD中,CN=AM,AE=CF求证:四边形MENF是平行四边形。1、已知,如图,在ABCD中,CN=AM,AE=CF求证:四边形MENF是平行四边形。1、知识方面:1)两组对边分别平行的四边形是平行四边形;2)一组对边平行且相等的四边形是平行四边形 3)两组对边分别相等的四边形是平行四边形2.思想方法方面:结合图形灵活选用判定方法 学生自我分析图形的个数,并阐明理由。教师用几何画板演示所找到的图形。学生再进一步分析MP与QN的数量关系。(说明:对于学生得到的结论,要适时点评,及时肯定,但教师要明确教学重点,进行取舍)分析:欲证四边形BFDE是平行四边形可以根据判定定理来证明.学生结合图形探究 。通过问题串的精心设计,引导学生对判定方法有深入的探究。 本节课安排了2个例题,例1是教材P96的例3,它是平行四边形的性质与判定的综合运用,此题最好先让学生说出证明的思路,然后老师总结并指出其最佳方法.例2都是补充的题目,其目的就是让学生能灵活和综合地运用平行四边形的判定方法和性质来解决问题.可以提高学生的动手能力和学生的思维能力,又可以提高学生的学习兴趣.本节课我们对平行四边形的判定进行了探究。通过这节课的学习,你有什么收获? 使学生熟悉定理的使用,刚开始使用定理,让学生画好图形,并标好图形,理清边之间的关系。让学生明确用四个不等边三角形拼一个如图的大三角形,让学生指出图中所有的平行四边形,并说明理由.引导学生自己小结本节课的知识要点及数学方法。
板书设计 19.1.2 平行四边形的判定 ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )(一)
例1 例2 练习 2
教学反思
