九年级数学二次函数与反比例函数练习题
图片预览
文档简介
二次函数与反比例函数练习题
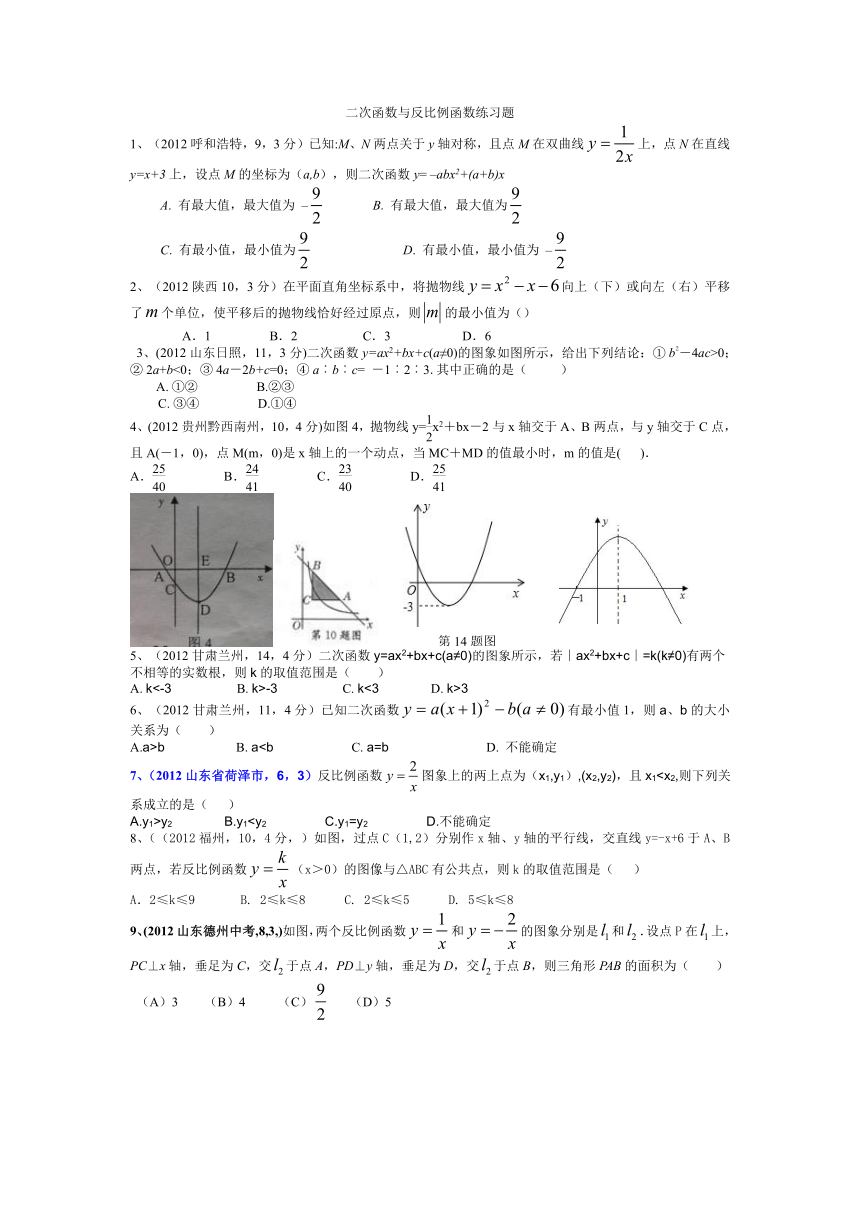
1、(2012呼和浩特,9,3分)已知:M、N两点关于y轴对称,且点M在双曲线上,点N在直线y=x+3上,设点M的坐标为(a,b),则二次函数y= –abx2+(a+b)x
A. 有最大值,最大值为 – B. 有最大值,最大值为
C. 有最小值,最小值为 D. 有最小值,最小值为 –
2、(2012陕西10,3分)在平面直角坐标系中,将抛物线向上(下)或向左(右)平移了个单位,使平移后的抛物线恰好经过原点,则的最小值为()
A.1 B.2 C.3 D.6
3、(2012山东日照,11,3分)二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出下列结论:① b2-4ac>0;② 2a+b<0;③ 4a-2b+c=0;④ a︰b︰c= -1︰2︰3.其中正确的是( )
A. ①② B.②③
C. ③④ D.①④
4、(2012贵州黔西南州,10,4分)如图4,抛物线y=x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(-1,0),点M(m,0)是x轴上的一个动点,当MC+MD的值最小时,m的值是( ).
A. B. C. D.
5、(2012甘肃兰州,14,4分)二次函数y=ax2+bx+c(a≠0)的图象所示,若∣ax2+bx+c∣=k(k≠0)有两个
不相等的实数根,则k的取值范围是( )
A. k<-3 B. k>-3 C. k<3 D. k>3
6、(2012甘肃兰州,11,4分)已知二次函数有最小值1,则a、b的大小关系为( )
A.a>b B. a7、(2012山东省荷泽市,6,3)反比例函数图象上的两上点为(x1,y1),(x2,y2),且x1A.y1>y2 B.y18、((2012福州,10,4分,)如图,过点C(1,2)分别作x轴、y轴的平行线,交直线y=-x+6于A、B两点,若反比例函数(x>0)的图像与△ABC有公共点,则k的取值范围是( )
A.2≤k≤9 B. 2≤k≤8 C. 2≤k≤5 D. 5≤k≤8
9、(2012山东德州中考,8,3,)如图,两个反比例函数和的图象分别是和.设点P在上,PC⊥x轴,垂足为C,交于点A,PD⊥y轴,垂足为D,交于点B,则三角形PAB的面积为( )
(A)3 (B)4 (C) (D)5
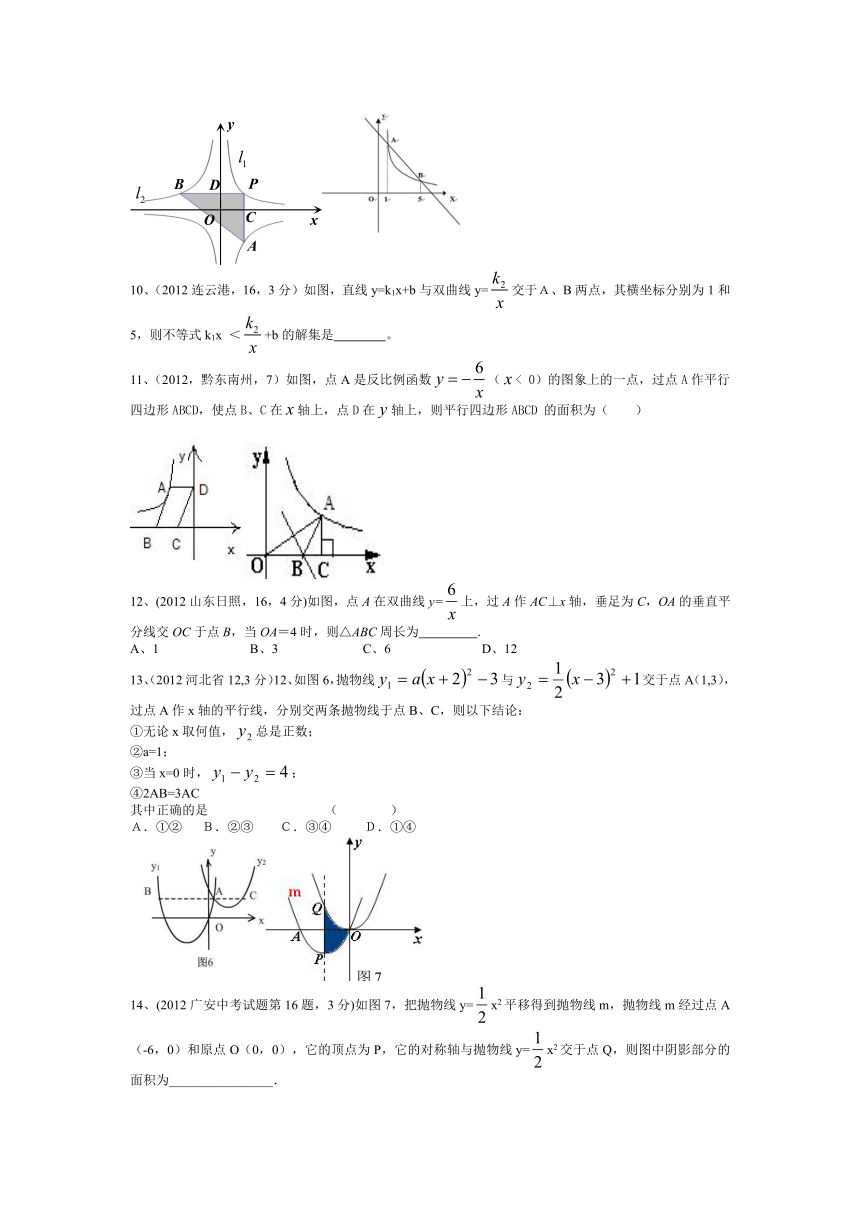
10、(2012连云港,16,3分)如图,直线y=k1x+b与双曲线y=交于A、B两点,其横坐标分别为1和5,则不等式k1x <+b的解集是 。
11、(2012,黔东南州,7)如图,点A是反比例函数(< 0)的图象上的一点,过点A作平行四边形ABCD,使点B、C在轴上,点D在轴上,则平行四边形ABCD 的面积为( )
12、(2012山东日照,16,4分)如图,点A在双曲线y=上,过A作AC⊥x轴,垂足为C,OA的垂直平分线交OC于点B,当OA=4时,则△ABC周长为 .
A、1 B、3 C、6 D、12
13、(2012河北省12,3分)12、如图6,抛物线与交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B、C,则以下结论:
①无论x取何值,总是正数;
②a=1;
③当x=0时,;
④2AB=3AC
其中正确的是 ( )
A.①② B.②③ C.③④ D.①④
14、(2012广安中考试题第16题,3分)如图7,把抛物线y=x2平移得到抛物线m,抛物线m经过点A(-6,0)和原点O(0,0),它的顶点为P,它的对称轴与抛物线y=x2交于点Q,则图中阴影部分的面积为________________.
15、(2012珠海,19,7分)如图,二次函数的图象与轴交于点C,点B是点C关于该二次函数图象的对称轴对称的点.已知一次函数y=kx+b的图象经过该二次函数图象上点A(1,0)及点B.
(1)求二次函数与一次函数的解析式;
(2)根据图象,写出满足kx+b≥的的取值范围.
16、(2012浙江省嘉兴市,21,10分)如图,一次函数=kx+b的图象与反比例函数=的图象相交于点A(2,3)和点B,与x轴相交于点C(8,0)。
(1)求这两个函数的解析式;
(2)当x取何值时, >.
17、(2012江西,19,8分)如图,等腰梯形ABCD放置在平面直角坐标系中,已知、、,反比例函数的图象经过点C.
(1)求C点坐标和反比例函数的解析式;
(2)将等腰梯形ABCD向上平移个单位后,使点B恰好落在双曲线上,求的值.
18、(2012浙江丽水8分,21题)(本题8分)如图,等边△OAB和等边△AFE的一边都在x轴上,双曲线y=(k>0)经过边OB的中点C和AE的中点D,已知等边△OAB的边长为4.
(1)求该双曲线所表示的函数解析式;
(2)求等边△AEF的边长.
19、(2012甘肃兰州,27,10分)若x1、x2是关于x一元二次方程ax2+bx+c=0(a≠0)的两个根,则方程的两个根x1、x2和系数a、b、c有如下关系:.把它们称为一元二次方程根与系数关系定理。如果设二次函数y=ax2+bx+c(a≠0)的图象与x轴的两个交点为A(x1,0),B(x2,0).利用根与系数关系定理可以得到A、B两个交点间的距离为:
参考以上定理和结论,解答下列问题:
设二次函数y=ax2+bx+c(a>0)的图象与x轴的两个交点A(x1,0),B(x2,0),抛物线的顶点为C,显然△ABC为等腰三角形.
(1)当△ABC为等腰直角三角形时,求的值;
(2)当△ABC为等边三角形时,求的值.
20、(2012安徽,21,12分)甲、乙两家商场进行促销活动,甲商场采用“慢200减100”的促销方式,即购买商品的总金额满200元但不足400元,少付100元;满400元但不足600元,少付200元;……,乙商场按顾客购买商品的总金额打6折促销。
(1)若顾客在甲商场购买了510元的商品,付款时应付多少钱?
解:
(2)若顾客在甲商场购买商品的总金额为x(400≤x<600)元,优惠后得到商家的优惠率为p(p=),写出p与x之间的函数关系式,并说明p随x的变化情况;
解:
(3)品牌、质量、规格等都相同的某种商品,在甲乙两商场的标价都是x(200≤x<400)元,你认为选择哪家商场购买商品花钱较少?请说明理由。
第14题图
x
y
A
P
B
D
C
O
图7
第27题图
1、(2012呼和浩特,9,3分)已知:M、N两点关于y轴对称,且点M在双曲线上,点N在直线y=x+3上,设点M的坐标为(a,b),则二次函数y= –abx2+(a+b)x
A. 有最大值,最大值为 – B. 有最大值,最大值为
C. 有最小值,最小值为 D. 有最小值,最小值为 –
2、(2012陕西10,3分)在平面直角坐标系中,将抛物线向上(下)或向左(右)平移了个单位,使平移后的抛物线恰好经过原点,则的最小值为()
A.1 B.2 C.3 D.6
3、(2012山东日照,11,3分)二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出下列结论:① b2-4ac>0;② 2a+b<0;③ 4a-2b+c=0;④ a︰b︰c= -1︰2︰3.其中正确的是( )
A. ①② B.②③
C. ③④ D.①④
4、(2012贵州黔西南州,10,4分)如图4,抛物线y=x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(-1,0),点M(m,0)是x轴上的一个动点,当MC+MD的值最小时,m的值是( ).
A. B. C. D.
5、(2012甘肃兰州,14,4分)二次函数y=ax2+bx+c(a≠0)的图象所示,若∣ax2+bx+c∣=k(k≠0)有两个
不相等的实数根,则k的取值范围是( )
A. k<-3 B. k>-3 C. k<3 D. k>3
6、(2012甘肃兰州,11,4分)已知二次函数有最小值1,则a、b的大小关系为( )
A.a>b B. a7、(2012山东省荷泽市,6,3)反比例函数图象上的两上点为(x1,y1),(x2,y2),且x1
A.2≤k≤9 B. 2≤k≤8 C. 2≤k≤5 D. 5≤k≤8
9、(2012山东德州中考,8,3,)如图,两个反比例函数和的图象分别是和.设点P在上,PC⊥x轴,垂足为C,交于点A,PD⊥y轴,垂足为D,交于点B,则三角形PAB的面积为( )
(A)3 (B)4 (C) (D)5
10、(2012连云港,16,3分)如图,直线y=k1x+b与双曲线y=交于A、B两点,其横坐标分别为1和5,则不等式k1x <+b的解集是 。
11、(2012,黔东南州,7)如图,点A是反比例函数(< 0)的图象上的一点,过点A作平行四边形ABCD,使点B、C在轴上,点D在轴上,则平行四边形ABCD 的面积为( )
12、(2012山东日照,16,4分)如图,点A在双曲线y=上,过A作AC⊥x轴,垂足为C,OA的垂直平分线交OC于点B,当OA=4时,则△ABC周长为 .
A、1 B、3 C、6 D、12
13、(2012河北省12,3分)12、如图6,抛物线与交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B、C,则以下结论:
①无论x取何值,总是正数;
②a=1;
③当x=0时,;
④2AB=3AC
其中正确的是 ( )
A.①② B.②③ C.③④ D.①④
14、(2012广安中考试题第16题,3分)如图7,把抛物线y=x2平移得到抛物线m,抛物线m经过点A(-6,0)和原点O(0,0),它的顶点为P,它的对称轴与抛物线y=x2交于点Q,则图中阴影部分的面积为________________.
15、(2012珠海,19,7分)如图,二次函数的图象与轴交于点C,点B是点C关于该二次函数图象的对称轴对称的点.已知一次函数y=kx+b的图象经过该二次函数图象上点A(1,0)及点B.
(1)求二次函数与一次函数的解析式;
(2)根据图象,写出满足kx+b≥的的取值范围.
16、(2012浙江省嘉兴市,21,10分)如图,一次函数=kx+b的图象与反比例函数=的图象相交于点A(2,3)和点B,与x轴相交于点C(8,0)。
(1)求这两个函数的解析式;
(2)当x取何值时, >.
17、(2012江西,19,8分)如图,等腰梯形ABCD放置在平面直角坐标系中,已知、、,反比例函数的图象经过点C.
(1)求C点坐标和反比例函数的解析式;
(2)将等腰梯形ABCD向上平移个单位后,使点B恰好落在双曲线上,求的值.
18、(2012浙江丽水8分,21题)(本题8分)如图,等边△OAB和等边△AFE的一边都在x轴上,双曲线y=(k>0)经过边OB的中点C和AE的中点D,已知等边△OAB的边长为4.
(1)求该双曲线所表示的函数解析式;
(2)求等边△AEF的边长.
19、(2012甘肃兰州,27,10分)若x1、x2是关于x一元二次方程ax2+bx+c=0(a≠0)的两个根,则方程的两个根x1、x2和系数a、b、c有如下关系:.把它们称为一元二次方程根与系数关系定理。如果设二次函数y=ax2+bx+c(a≠0)的图象与x轴的两个交点为A(x1,0),B(x2,0).利用根与系数关系定理可以得到A、B两个交点间的距离为:
参考以上定理和结论,解答下列问题:
设二次函数y=ax2+bx+c(a>0)的图象与x轴的两个交点A(x1,0),B(x2,0),抛物线的顶点为C,显然△ABC为等腰三角形.
(1)当△ABC为等腰直角三角形时,求的值;
(2)当△ABC为等边三角形时,求的值.
20、(2012安徽,21,12分)甲、乙两家商场进行促销活动,甲商场采用“慢200减100”的促销方式,即购买商品的总金额满200元但不足400元,少付100元;满400元但不足600元,少付200元;……,乙商场按顾客购买商品的总金额打6折促销。
(1)若顾客在甲商场购买了510元的商品,付款时应付多少钱?
解:
(2)若顾客在甲商场购买商品的总金额为x(400≤x<600)元,优惠后得到商家的优惠率为p(p=),写出p与x之间的函数关系式,并说明p随x的变化情况;
解:
(3)品牌、质量、规格等都相同的某种商品,在甲乙两商场的标价都是x(200≤x<400)元,你认为选择哪家商场购买商品花钱较少?请说明理由。
第14题图
x
y
A
P
B
D
C
O
图7
第27题图
