向量数量积的物理背景与定义
图片预览





文档简介
(共17张PPT)
F
位移S
O
A
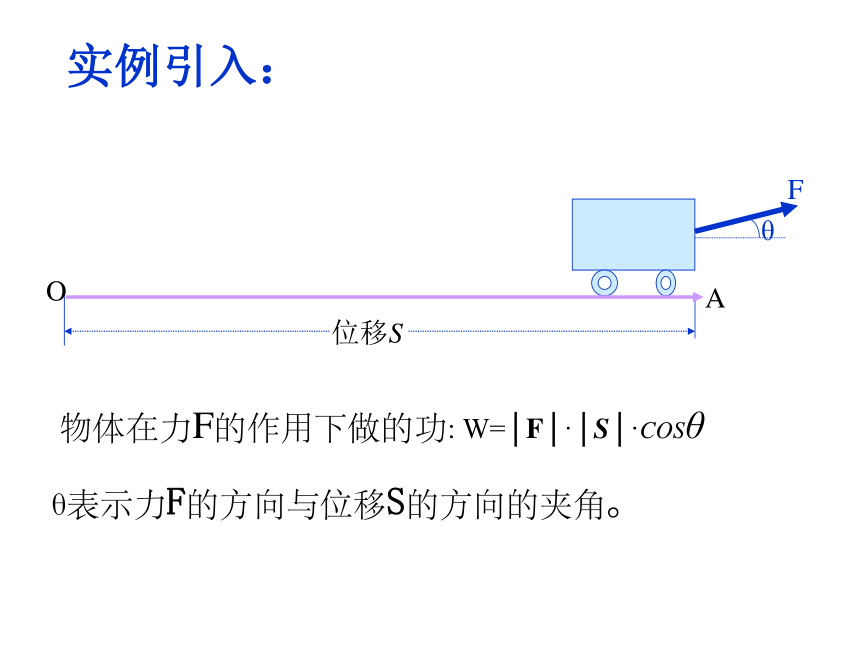
物体在力F的作用下做的功: W=│F│·│S│·COSθ
θ
θ表示力F的方向与位移S的方向的夹角。
实例引入:
一. 夹角的概念
已知两个非零向量 ,在平面上任取一点O,作OA= ,OB= ,则∠AOB叫做向量 与 的夹角。记作: 并规定:
说明:在两向量的夹角定义中,两相量必须是同起点的,对不是同起点的两个向量,要先将它们平移到同一起点。
O
A
B
(1)
O
B
A
(2)
练习:请指出下列图中两向量的夹角:
O
A
B
(4)
θ
(3)
A
O
B
O
A
B
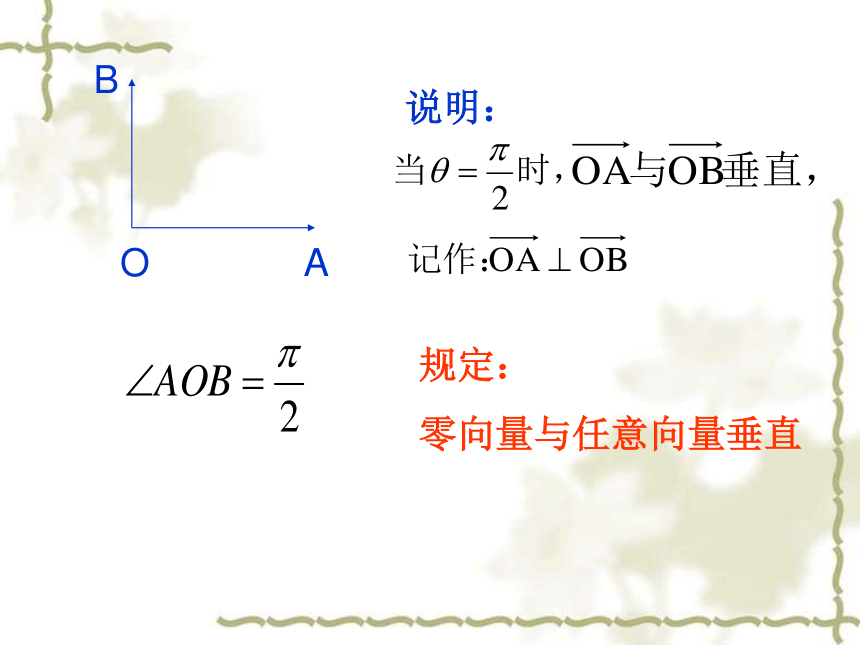
规定:
零向量与任意向量垂直
说明:
二、向量在轴上的正射影:
二、向量在轴上的正射影:
三.平面向量数量积(内积)的定义:
定义:
规定:零向量与任一向量的数量积为0
说明:(1)符号“.”在向量运算中不是实数运算中的乘 号,因此既不能省略也不能用“×”代替。
(2)两个向量的数量积是一个数量而不是向量。
_____________
________
____________
___________
____________
0
≤
课堂练习
判断下列各题是否正确
(1)若 ,则对任意向量 ,有
(2)若 ,则对任意非零向量 ,有
(3)若 ,且 ,则
(4)若 ,则
(5)对任意向量 有
(6)若 且 ,则
(√)
(× )
( ×)
(× )
(√ )
(× )
练习:
A
B
C
小结:
1、平面向量的数量积是一个实数,这个实数不仅与两个向量的模有关,还与这两个向量的夹角有关。
2、对于实际图形中的角,一定要确定是否是同一起点,是否为两个向量的夹角。
3、向量数量积的重要性质
作 业
P109:A组:1,2
B组:1(2)(3)
F
位移S
O
A
物体在力F的作用下做的功: W=│F│·│S│·COSθ
θ
θ表示力F的方向与位移S的方向的夹角。
实例引入:
一. 夹角的概念
已知两个非零向量 ,在平面上任取一点O,作OA= ,OB= ,则∠AOB叫做向量 与 的夹角。记作: 并规定:
说明:在两向量的夹角定义中,两相量必须是同起点的,对不是同起点的两个向量,要先将它们平移到同一起点。
O
A
B
(1)
O
B
A
(2)
练习:请指出下列图中两向量的夹角:
O
A
B
(4)
θ
(3)
A
O
B
O
A
B
规定:
零向量与任意向量垂直
说明:
二、向量在轴上的正射影:
二、向量在轴上的正射影:
三.平面向量数量积(内积)的定义:
定义:
规定:零向量与任一向量的数量积为0
说明:(1)符号“.”在向量运算中不是实数运算中的乘 号,因此既不能省略也不能用“×”代替。
(2)两个向量的数量积是一个数量而不是向量。
_____________
________
____________
___________
____________
0
≤
课堂练习
判断下列各题是否正确
(1)若 ,则对任意向量 ,有
(2)若 ,则对任意非零向量 ,有
(3)若 ,且 ,则
(4)若 ,则
(5)对任意向量 有
(6)若 且 ,则
(√)
(× )
( ×)
(× )
(√ )
(× )
练习:
A
B
C
小结:
1、平面向量的数量积是一个实数,这个实数不仅与两个向量的模有关,还与这两个向量的夹角有关。
2、对于实际图形中的角,一定要确定是否是同一起点,是否为两个向量的夹角。
3、向量数量积的重要性质
作 业
P109:A组:1,2
B组:1(2)(3)
