人教版数学七 年级上册4.1.1立体图形的展开图教案
文档属性
| 名称 | 人教版数学七 年级上册4.1.1立体图形的展开图教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 74.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-05 00:00:00 | ||
图片预览

文档简介
1.4 立体图形的展开图
教学目标:理解圆柱,圆锥,长方体,棱柱的展开图,掌握正方体的展开图的规律。
知识与技能:经历几何体表面展开的过程,认识几何体的表面展开图,并能根据所给几何体的表面展开图判定几何体的形状。
过程与方法:在操作活动中领悟表面展开图是用平面图形认识、研究几何体的重要手段,使学生体会转化的方法。
情感态度与价值观:通过有趣的几何体表面展开活动,培养学生的兴趣。
教学重点:了解基本几何体与其展开图的关系,体会一个立体图形可以有多种展开图。
教学难点:利用想象,把展开图叠成几何体。
教材分析:把立体图形展成平面图形是研究几何图形的重要手段,是学生意识中很陌生但又非常必要的过程,特别是同一立体图形可以展成不同形式的平面展开图,其间蕴藏着发散思维。要收到较好效果,一定要有深刻的体验、足量的练习。
教学方法:合作探究
课时安排:1课时
环节 教 师 活 动 学生活动 设 计 意 图
情景引入 复习提问:.立体图形都包括那些球体,柱体,椎体1.设疑:.小壁虎的难题:如图,一只圆桶的下方有一只壁虎,上方有一只蚊子,壁虎想要尽快吃到蚊子,应该走哪条路径? 2.立体图形展开成平面图形(1)生活中的精美包装(2)猜想立体图形的展开图观察 高 底的周长 学生回答观察,猜测思考,观看观察学生思考。 复习旧知识,为学习新内容做铺垫。自然引入新课。设置疑问,以激发学生的求知欲望。精美的图形,熟悉的事物,有悬念的问题,激起学生兴趣。通过课件展示使学生掌握常见圆柱的展开图
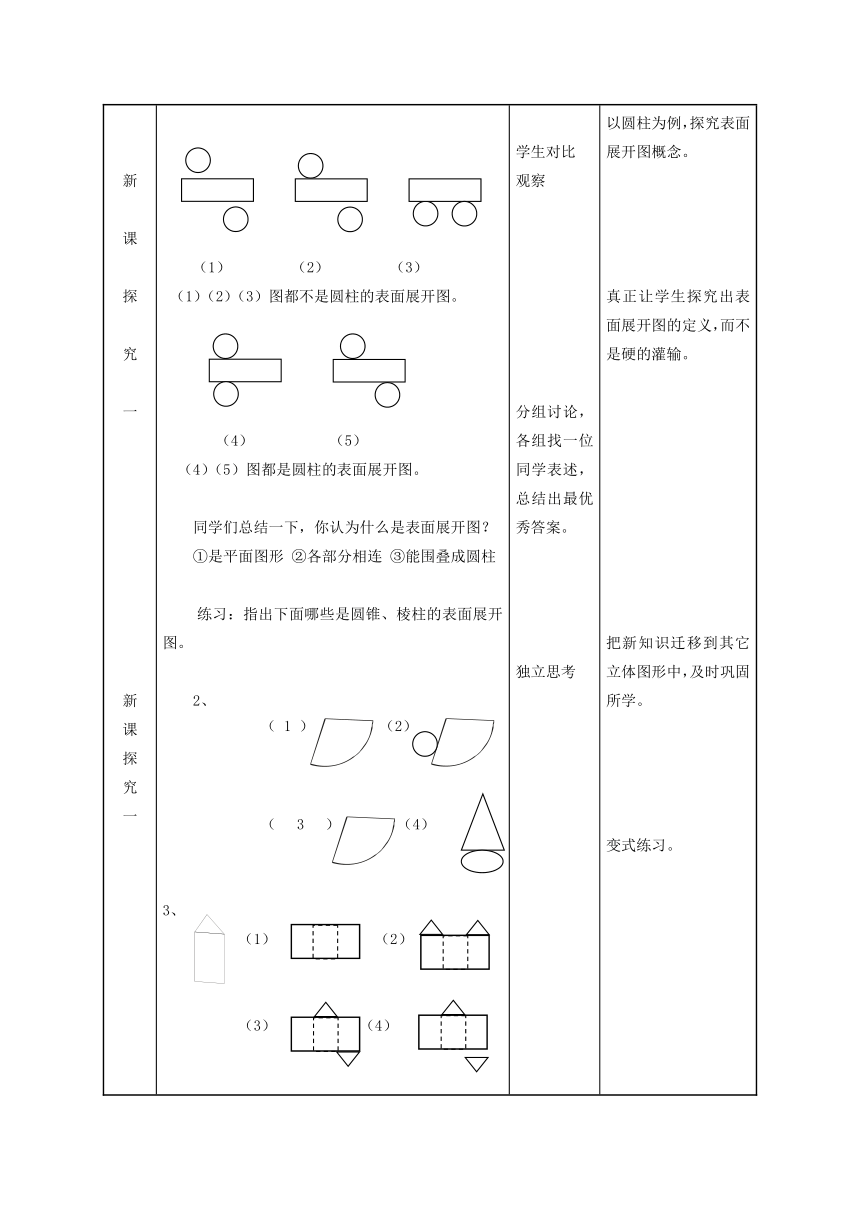
新课探究一新课探究一 1、用课件演示图:(1) (2) (3)(1)(2)(3)图都不是圆柱的表面展开图。(4) (5)(4)(5)图都是圆柱的表面展开图。同学们总结一下,你认为什么是表面展开图?①是平面图形 ②各部分相连 ③能围叠成圆柱练习:指出下面哪些是圆锥、棱柱的表面展开图。2、 (1) (2) (3) (4)3、 (1) (2) (3) (4) 学生对比观察分组讨论,各组找一位同学表述,总结出最优秀答案。独立思考 以圆柱为例,探究表面展开图概念。真正让学生探究出表面展开图的定义,而不是硬的灌输。把新知识迁移到其它立体图形中,及时巩固所学。变式练习。
新课探究二 1学生们拿出事先做好的m的立方体,把立方体展成表面展开图形式。(1)以四人为一组,看哪个组的展开图形式最多?(2)如何才能得到更多的形式?把各棱编上1—12的序号,剪开七条棱。各组选出代表展示,把展开图粘到黑板上用课件展示:①1.4.1型 ②2.3.1型③2.2.2 ④3.32大家能较容易的把手边的展开图折成立方体,你能辨别出下边的平面图形能否折成立方体吗?(1) (2)把正方体展开时,大家把棱编上号码,对研究起了很大作用,现在怎样在每个正方形上做标记呢?标上底、上、前、后、左、右。 学生动手操作。学生们合作交流。学生观察学生动手把得到的展开图折成立方体。展开想象。 分组便于讨论合作。学生经历从立体图形到平面图形的变化过程。正方体各棱上编号便于学生小组协作。完善逆向思维。加强空间观念。
课堂总
结 1、基础题组2.在没有数字的方格内填入数,使折成正方体后相对面上的数互为相反数3.下边的4个图形中,哪一个是由左边的盒子展开而成的4.下面是一多面体的展开图,折叠成立方体后使字在正方体的外表面。根据要求回答:5.解决课前设疑的问题 独立完成学生猜测,动手折一折,进而验证猜测,得出结论。学生独立解决 正方体的展开图的训练。体现从猜测—动手实践---讨论—得出结论,培养学生分析问题和解决问题的能力。收尾呼应
课堂总
结 请学生谈:1.收获2.质疑 回忆总结 学生反思
附:板书设计
教学反思:
本节课从学生学过的旧知识入手,充分利用学生已有的知识,让学生对圆柱展开图的分类,体验出展开图的定义,之后把所学进行横向推广,最后动手操作,对立方体进行展开,对展开图进行折叠,使学生亲历了三维空间与二维平面之间的联系,形成一个学习环。在学习过程中,多次启发学生寻找思考问题的方法,探究动手操作的规律,因此学生得到体验,感悟的同时,也完善了认知结构。在教学过中程中教师过分追求完美,结果造成面面俱到,反而有偏离重点。
侧 面
展开图
1.4 立体图形的展开图
立体图形 圆柱 圆锥 棱柱 正方体
折叠 展开
平面图形(相连) 两个圆 扇形 长方形 六个正方
+ + + 形相连
长方形 圆 长方形
教学目标:理解圆柱,圆锥,长方体,棱柱的展开图,掌握正方体的展开图的规律。
知识与技能:经历几何体表面展开的过程,认识几何体的表面展开图,并能根据所给几何体的表面展开图判定几何体的形状。
过程与方法:在操作活动中领悟表面展开图是用平面图形认识、研究几何体的重要手段,使学生体会转化的方法。
情感态度与价值观:通过有趣的几何体表面展开活动,培养学生的兴趣。
教学重点:了解基本几何体与其展开图的关系,体会一个立体图形可以有多种展开图。
教学难点:利用想象,把展开图叠成几何体。
教材分析:把立体图形展成平面图形是研究几何图形的重要手段,是学生意识中很陌生但又非常必要的过程,特别是同一立体图形可以展成不同形式的平面展开图,其间蕴藏着发散思维。要收到较好效果,一定要有深刻的体验、足量的练习。
教学方法:合作探究
课时安排:1课时
环节 教 师 活 动 学生活动 设 计 意 图
情景引入 复习提问:.立体图形都包括那些球体,柱体,椎体1.设疑:.小壁虎的难题:如图,一只圆桶的下方有一只壁虎,上方有一只蚊子,壁虎想要尽快吃到蚊子,应该走哪条路径? 2.立体图形展开成平面图形(1)生活中的精美包装(2)猜想立体图形的展开图观察 高 底的周长 学生回答观察,猜测思考,观看观察学生思考。 复习旧知识,为学习新内容做铺垫。自然引入新课。设置疑问,以激发学生的求知欲望。精美的图形,熟悉的事物,有悬念的问题,激起学生兴趣。通过课件展示使学生掌握常见圆柱的展开图
新课探究一新课探究一 1、用课件演示图:(1) (2) (3)(1)(2)(3)图都不是圆柱的表面展开图。(4) (5)(4)(5)图都是圆柱的表面展开图。同学们总结一下,你认为什么是表面展开图?①是平面图形 ②各部分相连 ③能围叠成圆柱练习:指出下面哪些是圆锥、棱柱的表面展开图。2、 (1) (2) (3) (4)3、 (1) (2) (3) (4) 学生对比观察分组讨论,各组找一位同学表述,总结出最优秀答案。独立思考 以圆柱为例,探究表面展开图概念。真正让学生探究出表面展开图的定义,而不是硬的灌输。把新知识迁移到其它立体图形中,及时巩固所学。变式练习。
新课探究二 1学生们拿出事先做好的m的立方体,把立方体展成表面展开图形式。(1)以四人为一组,看哪个组的展开图形式最多?(2)如何才能得到更多的形式?把各棱编上1—12的序号,剪开七条棱。各组选出代表展示,把展开图粘到黑板上用课件展示:①1.4.1型 ②2.3.1型③2.2.2 ④3.32大家能较容易的把手边的展开图折成立方体,你能辨别出下边的平面图形能否折成立方体吗?(1) (2)把正方体展开时,大家把棱编上号码,对研究起了很大作用,现在怎样在每个正方形上做标记呢?标上底、上、前、后、左、右。 学生动手操作。学生们合作交流。学生观察学生动手把得到的展开图折成立方体。展开想象。 分组便于讨论合作。学生经历从立体图形到平面图形的变化过程。正方体各棱上编号便于学生小组协作。完善逆向思维。加强空间观念。
课堂总
结 1、基础题组2.在没有数字的方格内填入数,使折成正方体后相对面上的数互为相反数3.下边的4个图形中,哪一个是由左边的盒子展开而成的4.下面是一多面体的展开图,折叠成立方体后使字在正方体的外表面。根据要求回答:5.解决课前设疑的问题 独立完成学生猜测,动手折一折,进而验证猜测,得出结论。学生独立解决 正方体的展开图的训练。体现从猜测—动手实践---讨论—得出结论,培养学生分析问题和解决问题的能力。收尾呼应
课堂总
结 请学生谈:1.收获2.质疑 回忆总结 学生反思
附:板书设计
教学反思:
本节课从学生学过的旧知识入手,充分利用学生已有的知识,让学生对圆柱展开图的分类,体验出展开图的定义,之后把所学进行横向推广,最后动手操作,对立方体进行展开,对展开图进行折叠,使学生亲历了三维空间与二维平面之间的联系,形成一个学习环。在学习过程中,多次启发学生寻找思考问题的方法,探究动手操作的规律,因此学生得到体验,感悟的同时,也完善了认知结构。在教学过中程中教师过分追求完美,结果造成面面俱到,反而有偏离重点。
侧 面
展开图
1.4 立体图形的展开图
立体图形 圆柱 圆锥 棱柱 正方体
折叠 展开
平面图形(相连) 两个圆 扇形 长方形 六个正方
+ + + 形相连
长方形 圆 长方形
