人教版数学九年级上册22.1.3二次函数y=a(x-h)2+k的图像和性质教学设计
文档属性
| 名称 | 人教版数学九年级上册22.1.3二次函数y=a(x-h)2+k的图像和性质教学设计 |  | |
| 格式 | doc | ||
| 文件大小 | 145.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-05 10:14:08 | ||
图片预览

文档简介
教学目标 知识技能 1.会画二次函数的顶点式y=a (x-h)2+k的图象;2.掌握二次函数y=a (x-h)2+k的性质;3.会应用二次函数y=a (x-h)2+k的性质解题.
数学思考 经历函数y=a (x-h)2+k图象画法与性质的探索过程,体会“数”“形”结合的数学思想。
解决问题 体会数形结合的数学思想在问题解决中的作用,并能运用性质、图象及数形结合思想解决相关函数问题。
情感态度 1.在动手操作过程中,培养学生的合作意识和大胆猜想、乐于探究的良好品质。2.体验“数”与“形”的转化过程,感受函数图象的简洁美。激发学生学数学的兴趣。
教学重点 掌握二次函数y=a (x-h)2+k的性质;
教学难点 掌握二次函数y=a (x-h)2+k的性质,并会应用;
教学方法 自主探究、合作交流
教学模式 引入问题——师生探究——得出结论——练习应用
课题:二次函数的图象与性质
教学流程安排
活动流程图 活动内容和目的
活动1. 旧知回顾,引入课题 由问题引入,创设情境。
活动2. 课前预习,成果展示 学生小组展示展示自己预习的成果。
活动3. 作图观察,总结规律 动手操作,猜想、验证,合作交流,给学生提供充分从事数学活动的机会,创造揭示数学规律的环境
活动4. 牛刀小试,成果展示 灵活运用所学知识,解决实际问题。
活动5. 课堂练习,小组竞争 学生限时练习,完成指定练习,小组竞争,合作交流。
活动6. 课堂小结,推荐作业 理清本节所学知识.总结情感收获,巩固应用。
教学过程设计
问题与情境 师生行为 设计意图
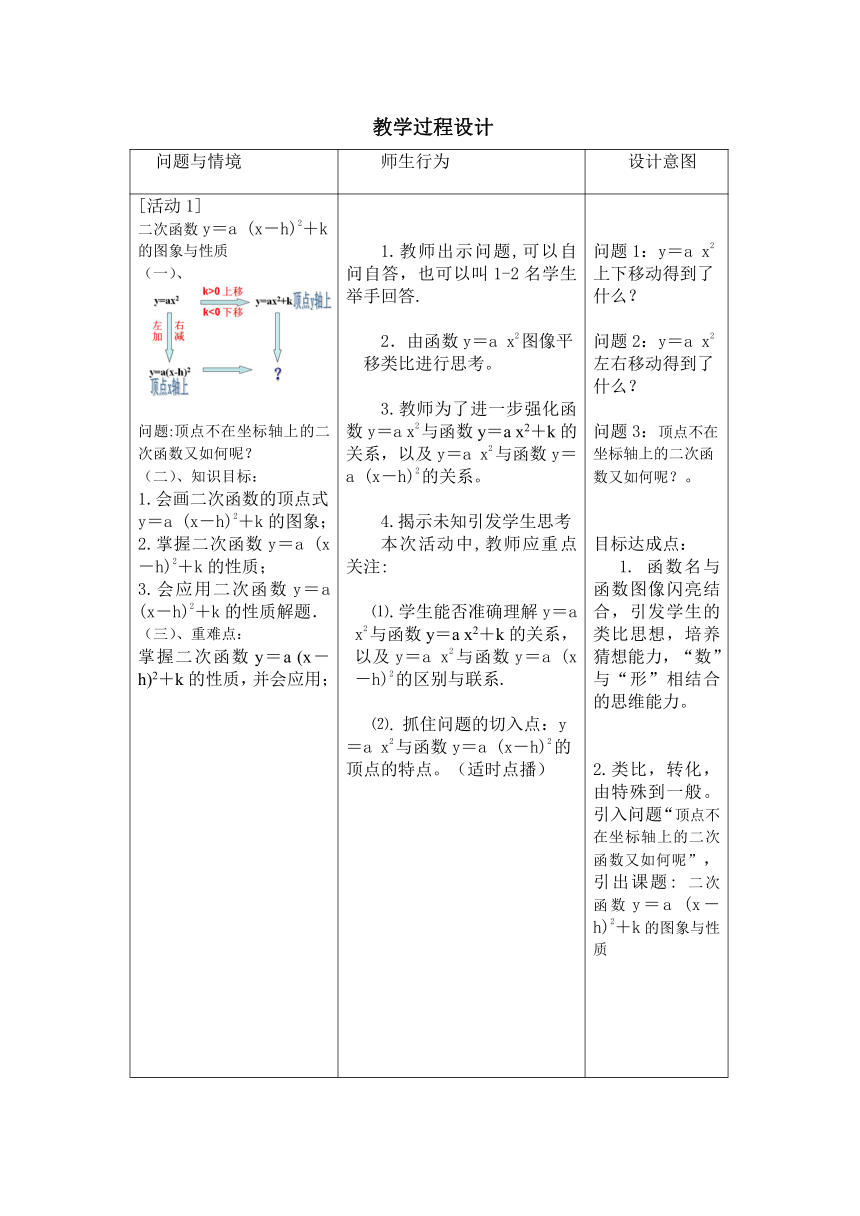
[活动1]二次函数y=a (x-h)2+k的图象与性质(一)、问题:顶点不在坐标轴上的二次函数又如何呢?(二)、知识目标:1.会画二次函数的顶点式y=a (x-h)2+k的图象;2.掌握二次函数y=a (x-h)2+k的性质;3.会应用二次函数y=a (x-h)2+k的性质解题.(三)、重难点:掌握二次函数y=a (x-h)2+k的性质,并会应用; 1.教师出示问题,可以自问自答,也可以叫1-2名学生举手回答.2.由函数y=a x2图像平移类比进行思考。3.教师为了进一步强化函数y=a x2与函数y=a x2+k的关系,以及y=a x2与函数y=a (x-h)2的关系。 4.揭示未知引发学生思考本次活动中,教师应重点关注:⑴.学生能否准确理解y=a x2与函数y=a x2+k的关系,以及y=a x2与函数y=a (x-h)2的区别与联系.⑵. 抓住问题的切入点:y=a x2与函数y=a (x-h)2的顶点的特点。(适时点播) 问题1:y=a x2上下移动得到了什么?问题2:y=a x2左右移动得到了什么?问题3:顶点不在坐标轴上的二次函数又如何呢?。目标达成点:1. 函数名与函数图像闪亮结合,引发学生的类比思想,培养猜想能力,“数”与“形”相结合的思维能力。2.类比,转化,由特殊到一般。引入问题“顶点不在坐标轴上的二次函数又如何呢”,引出课题: 二次函数y=a (x-h)2+k的图象与性质
问题与情境 师生行为 设计意图
[活动2] 小组预习成果展示旧知回顾:1、将二次函数的图象向上平移2个单位,所得图象的解析式为 。2、将抛物线的图象向左平移3个单位后的抛物线的解析式为 。教材助读:1、二次函数y=a (x-h)2+k与有怎样的联系?2、二次函数y=a (x-h)2+k有哪些性质? 1.本内容由学生事先完成,在课堂上进行成果展示。 2.给学生讨论时间,分工合作,小组展示。自学成果展示。3.学生点评,促进数学情商教育,激发学生的数学学习热情。本次活动中,教师应重点关注: (1). 学生能否呈现出y=a x2与函数y=a x2+k的关系,以及y=a x2与函数y=a (x-h)2的关系.(2).学生能否理解二次函数y=a (x-h)2+k与有什么“形”上联系?总结、归纳出y=a (x-h)2+k的性质.(对于五个性质不要求说全) 意图1:检查前面内容学生的学习情况. 意图2:调查了解学生对新课y=a (x-h)2+k的预习情况.意图3:学生在讲台的成果展示,更容易吸引学生的注意力,更容易激发学生学习的热情。目标达成点: 1.旧知回顾是学生承上启下的切入点,是整个课题的切入点,老师在有必要的情况下可以点播。2.性质的得出,知识为了促进学生去思考,给学生思考的方向,思维的空间,所以这里学生能答出多少都应该鼓励。
问题与情境 师生行为 设计意图
[活动3] 探究一、二次函数y=a (x-h)2+k的图象与性质一、你能作出的图象吗? 列表-描点-连线观察:问题1:开口方向,顶点坐标,对称轴情况?问题2:形状变化?值变化?平移关系如何?问题3:抛物线是由 如何平移得到的?三、知识梳理(一)抛物线的特点:1、 当时,开口向 ;当时,开口 ;2、顶点坐标是 ;3.对称轴是直线 。(二抛物线与形状 ,位置不同,是由平移得到的。二次函数图象的平移规律:左 右 ,上 下 。(三)平移前后的两条抛物线值 。 1.学生独立思考完成列表、描点、连线。 可以叫一个学生上黑板完成。2.学生观察图像,得出结论。3.学生根据自己所得,完成几个填空题。教师巡视,适时点播,4. 学生纠错,老师讲评。 5.师生进一步总结,得出结论。叫学生(一起)总结规律,得出结论(一起读) 本次活动中,教师应重点关注:(1).学生有充足的时间探索函数y=(x-1)2性质.(2). 后面几个填空,是引导学生去思考的,旨在“抛砖引玉”,使得学生产生思维的火花,层层推进,进而得出结论。 意图1、函数的性质引出的常规作法作图-观察-得出结论。意图2,几个填空题完成是学生思维的方向 意图3取点观察,帮助学生从感性认识上升到理性认识,形象直观的迁移到“形”与“数”转化。 意图4:理解性质结论的来龙去脉。目标达成点:1、作图观察,推动数形结合的思想。2、通过类比,转换,得出结论。提升学生整理归纳的能力。
问题与情境 师生行为 设计意图
[活动4]看预习自测探究二、二次函数y=a (x-h)2+k图像和性质应用例1、 已知二次函数y=2(x-3)2+1.下列说法:①其图象的开口向下;②其图象的对称轴为直线x=-3;③其图象顶点坐标为(3,-1);④当x<3时,y随x的增大而减小.则其中说法正确的有( )变式:已知为任意实数,则抛物线y=a(x-k)2+k的顶点在( )A.在轴上 B.在轴上 C.在直线y=x D.y=-x探究三、二次函数y=a (x-h)2+k图像的平移规律例2、若将抛物线向右平移3个单位,再向上平移1个单位后得到抛物线解析式为________________变式:抛物线y=2(x-n)2+m向右平移3个单位,再向下平移2个单位后得到抛物线y=2(x+1)2-3,则, 1.对事先完成的预习自测的答案,有争议的地方讲讲,否则不讲,给学生思维空间。 2.小组展示探究二、探究三,学生学习成果展示。 3.学生点评,加深学生认知碰撞。4.教师点评,给予学生积极的肯定,对题型做总结。本次活动中,教师应重点关注:(1)预习自测中学生全对的情况。 (2)学生在讲探究一探究二中解题思路的体现,有没有总结。 学完知识点,学生跃跃欲试终有机会一展身手1、对预习自测增大学生对自我预习成果的认知,提升学生预习的热情。 2.例题1及其变式主要是侧重于顶点式五个性质的应用。答案在其次,解题思路及其,规律总结还是重重之重。 3.例题2及其变式主要是侧重于顶点式与y=ax2之间的关系。解题的步骤还是关键所。4.探究二探究三不光是锤炼一下知识点,更是看学生对题型熟悉到了哪一步。
问题与情境 师生行为 设计意图
[活动5] 完成课堂练习A组 2.推荐作业教科书93第2、3题 1.独立完成定时课堂练习A组,分练习一、练习二随机抽二个组上黑板做题。 2.下面的同学做题,可以质疑台上同学的错误。 本次活动中,教师应重点关注:对于不同层次的学生速度有有快有慢,快的可以做一下B组和C组。结束后老师点评,对于错误的题型讲评,对于学生学习成果给予肯定。 1.学生独立完成习题自我检测。 2.小组竞争让学生体会成功的喜悦。3.老师及时给予学生肯定。
问题与情境 师生行为 设计意图
[活动6] 课堂检测课余完成。1.课堂小结:本节课你学到了那些知识,在知识的探究和运用过程中你有何体会?2.作业 课堂检测,练习B组C组教科书37页练习全品 1.教师引导学生积极思考,总结本节课的收获。时间允许的话可以叫学生总结。时间不够的话,老师带学生一同回顾。 2.教师布置作业,学生按层次完成作业. 本次活动中,教师应重点关注:(1)积极了解不同层次的学生对本节内容的认知情况。(2)理清本节所学知识,总结情感收获.数学知识与实际运用的密切关系. 1.帮助学生理清本节所学知识.总结情感收获. 2. 巩固所学知识,选做题,分层练习,给学生足够的自信心,又给学生发展的空间.
PAGE
数学思考 经历函数y=a (x-h)2+k图象画法与性质的探索过程,体会“数”“形”结合的数学思想。
解决问题 体会数形结合的数学思想在问题解决中的作用,并能运用性质、图象及数形结合思想解决相关函数问题。
情感态度 1.在动手操作过程中,培养学生的合作意识和大胆猜想、乐于探究的良好品质。2.体验“数”与“形”的转化过程,感受函数图象的简洁美。激发学生学数学的兴趣。
教学重点 掌握二次函数y=a (x-h)2+k的性质;
教学难点 掌握二次函数y=a (x-h)2+k的性质,并会应用;
教学方法 自主探究、合作交流
教学模式 引入问题——师生探究——得出结论——练习应用
课题:二次函数的图象与性质
教学流程安排
活动流程图 活动内容和目的
活动1. 旧知回顾,引入课题 由问题引入,创设情境。
活动2. 课前预习,成果展示 学生小组展示展示自己预习的成果。
活动3. 作图观察,总结规律 动手操作,猜想、验证,合作交流,给学生提供充分从事数学活动的机会,创造揭示数学规律的环境
活动4. 牛刀小试,成果展示 灵活运用所学知识,解决实际问题。
活动5. 课堂练习,小组竞争 学生限时练习,完成指定练习,小组竞争,合作交流。
活动6. 课堂小结,推荐作业 理清本节所学知识.总结情感收获,巩固应用。
教学过程设计
问题与情境 师生行为 设计意图
[活动1]二次函数y=a (x-h)2+k的图象与性质(一)、问题:顶点不在坐标轴上的二次函数又如何呢?(二)、知识目标:1.会画二次函数的顶点式y=a (x-h)2+k的图象;2.掌握二次函数y=a (x-h)2+k的性质;3.会应用二次函数y=a (x-h)2+k的性质解题.(三)、重难点:掌握二次函数y=a (x-h)2+k的性质,并会应用; 1.教师出示问题,可以自问自答,也可以叫1-2名学生举手回答.2.由函数y=a x2图像平移类比进行思考。3.教师为了进一步强化函数y=a x2与函数y=a x2+k的关系,以及y=a x2与函数y=a (x-h)2的关系。 4.揭示未知引发学生思考本次活动中,教师应重点关注:⑴.学生能否准确理解y=a x2与函数y=a x2+k的关系,以及y=a x2与函数y=a (x-h)2的区别与联系.⑵. 抓住问题的切入点:y=a x2与函数y=a (x-h)2的顶点的特点。(适时点播) 问题1:y=a x2上下移动得到了什么?问题2:y=a x2左右移动得到了什么?问题3:顶点不在坐标轴上的二次函数又如何呢?。目标达成点:1. 函数名与函数图像闪亮结合,引发学生的类比思想,培养猜想能力,“数”与“形”相结合的思维能力。2.类比,转化,由特殊到一般。引入问题“顶点不在坐标轴上的二次函数又如何呢”,引出课题: 二次函数y=a (x-h)2+k的图象与性质
问题与情境 师生行为 设计意图
[活动2] 小组预习成果展示旧知回顾:1、将二次函数的图象向上平移2个单位,所得图象的解析式为 。2、将抛物线的图象向左平移3个单位后的抛物线的解析式为 。教材助读:1、二次函数y=a (x-h)2+k与有怎样的联系?2、二次函数y=a (x-h)2+k有哪些性质? 1.本内容由学生事先完成,在课堂上进行成果展示。 2.给学生讨论时间,分工合作,小组展示。自学成果展示。3.学生点评,促进数学情商教育,激发学生的数学学习热情。本次活动中,教师应重点关注: (1). 学生能否呈现出y=a x2与函数y=a x2+k的关系,以及y=a x2与函数y=a (x-h)2的关系.(2).学生能否理解二次函数y=a (x-h)2+k与有什么“形”上联系?总结、归纳出y=a (x-h)2+k的性质.(对于五个性质不要求说全) 意图1:检查前面内容学生的学习情况. 意图2:调查了解学生对新课y=a (x-h)2+k的预习情况.意图3:学生在讲台的成果展示,更容易吸引学生的注意力,更容易激发学生学习的热情。目标达成点: 1.旧知回顾是学生承上启下的切入点,是整个课题的切入点,老师在有必要的情况下可以点播。2.性质的得出,知识为了促进学生去思考,给学生思考的方向,思维的空间,所以这里学生能答出多少都应该鼓励。
问题与情境 师生行为 设计意图
[活动3] 探究一、二次函数y=a (x-h)2+k的图象与性质一、你能作出的图象吗? 列表-描点-连线观察:问题1:开口方向,顶点坐标,对称轴情况?问题2:形状变化?值变化?平移关系如何?问题3:抛物线是由 如何平移得到的?三、知识梳理(一)抛物线的特点:1、 当时,开口向 ;当时,开口 ;2、顶点坐标是 ;3.对称轴是直线 。(二抛物线与形状 ,位置不同,是由平移得到的。二次函数图象的平移规律:左 右 ,上 下 。(三)平移前后的两条抛物线值 。 1.学生独立思考完成列表、描点、连线。 可以叫一个学生上黑板完成。2.学生观察图像,得出结论。3.学生根据自己所得,完成几个填空题。教师巡视,适时点播,4. 学生纠错,老师讲评。 5.师生进一步总结,得出结论。叫学生(一起)总结规律,得出结论(一起读) 本次活动中,教师应重点关注:(1).学生有充足的时间探索函数y=(x-1)2性质.(2). 后面几个填空,是引导学生去思考的,旨在“抛砖引玉”,使得学生产生思维的火花,层层推进,进而得出结论。 意图1、函数的性质引出的常规作法作图-观察-得出结论。意图2,几个填空题完成是学生思维的方向 意图3取点观察,帮助学生从感性认识上升到理性认识,形象直观的迁移到“形”与“数”转化。 意图4:理解性质结论的来龙去脉。目标达成点:1、作图观察,推动数形结合的思想。2、通过类比,转换,得出结论。提升学生整理归纳的能力。
问题与情境 师生行为 设计意图
[活动4]看预习自测探究二、二次函数y=a (x-h)2+k图像和性质应用例1、 已知二次函数y=2(x-3)2+1.下列说法:①其图象的开口向下;②其图象的对称轴为直线x=-3;③其图象顶点坐标为(3,-1);④当x<3时,y随x的增大而减小.则其中说法正确的有( )变式:已知为任意实数,则抛物线y=a(x-k)2+k的顶点在( )A.在轴上 B.在轴上 C.在直线y=x D.y=-x探究三、二次函数y=a (x-h)2+k图像的平移规律例2、若将抛物线向右平移3个单位,再向上平移1个单位后得到抛物线解析式为________________变式:抛物线y=2(x-n)2+m向右平移3个单位,再向下平移2个单位后得到抛物线y=2(x+1)2-3,则, 1.对事先完成的预习自测的答案,有争议的地方讲讲,否则不讲,给学生思维空间。 2.小组展示探究二、探究三,学生学习成果展示。 3.学生点评,加深学生认知碰撞。4.教师点评,给予学生积极的肯定,对题型做总结。本次活动中,教师应重点关注:(1)预习自测中学生全对的情况。 (2)学生在讲探究一探究二中解题思路的体现,有没有总结。 学完知识点,学生跃跃欲试终有机会一展身手1、对预习自测增大学生对自我预习成果的认知,提升学生预习的热情。 2.例题1及其变式主要是侧重于顶点式五个性质的应用。答案在其次,解题思路及其,规律总结还是重重之重。 3.例题2及其变式主要是侧重于顶点式与y=ax2之间的关系。解题的步骤还是关键所。4.探究二探究三不光是锤炼一下知识点,更是看学生对题型熟悉到了哪一步。
问题与情境 师生行为 设计意图
[活动5] 完成课堂练习A组 2.推荐作业教科书93第2、3题 1.独立完成定时课堂练习A组,分练习一、练习二随机抽二个组上黑板做题。 2.下面的同学做题,可以质疑台上同学的错误。 本次活动中,教师应重点关注:对于不同层次的学生速度有有快有慢,快的可以做一下B组和C组。结束后老师点评,对于错误的题型讲评,对于学生学习成果给予肯定。 1.学生独立完成习题自我检测。 2.小组竞争让学生体会成功的喜悦。3.老师及时给予学生肯定。
问题与情境 师生行为 设计意图
[活动6] 课堂检测课余完成。1.课堂小结:本节课你学到了那些知识,在知识的探究和运用过程中你有何体会?2.作业 课堂检测,练习B组C组教科书37页练习全品 1.教师引导学生积极思考,总结本节课的收获。时间允许的话可以叫学生总结。时间不够的话,老师带学生一同回顾。 2.教师布置作业,学生按层次完成作业. 本次活动中,教师应重点关注:(1)积极了解不同层次的学生对本节内容的认知情况。(2)理清本节所学知识,总结情感收获.数学知识与实际运用的密切关系. 1.帮助学生理清本节所学知识.总结情感收获. 2. 巩固所学知识,选做题,分层练习,给学生足够的自信心,又给学生发展的空间.
PAGE
同课章节目录
