人教版数学九年级上册23.1图形与变换——平移、旋转和轴对称教案
文档属性
| 名称 | 人教版数学九年级上册23.1图形与变换——平移、旋转和轴对称教案 |  | |
| 格式 | doc | ||
| 文件大小 | 304.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-05 10:36:53 | ||
图片预览

文档简介
图形与变换(1)——平移、旋转和轴对称
一、教学目标:
(1)能借助图形识别平移、旋转和轴对称三种基本变换的异同;
(2)能利用平移、旋转和轴对称三种变换认识基本图形并解决图形中的问题。
二、教学重点与难点
重点:利用变换认识图形的能力训练;
难点:应用变换找规律的能力训练。
三、教学过程:
1、借助图形,识别变换
如图,长方形ABCD中,对角线AC与BD
相交于O,DE∥AC,CE∥BD,那么△ABD
可以看作是由△__________旋转得到,旋转中心是_______,△DEC可以看作是由△__________经过 变换得到;有没有与△DEC成轴对称的三角形?中心对称呢?图中还有没有其它类似的图形变换?
通过回顾图形的三种变换,归纳总结如下
图形变换 共性 个性
轴对称 (1)形状不变、大小不变;(2)变换前后,两个图形全等,对应线段、对应角相等 对应点的连线段被对称轴垂直平分
平移 ①①对应线段平行(或在同一直线上)且相等;②对应点的连线段平行(或在同一直线上)且相等。
旋转 ①①对应点到旋转中心的距离相等. ②图形上的每个点都绕旋转中心沿相同方向转动了同样的角度.(即任意一对对应点与旋转中心的连线所成的角都是旋转角)
(意图:通过改编教材中的一道练习题,以题引入,借助图形帮助学生回顾图形的三种变换以及识别变换的异同)
2、训练与探索
环节1:动手练习,明确变换
1. 同学们曾玩过万花筒,它是由三块等宽等长的玻璃片围成的.
右图是看到的万花筒的一个图案,图中所有小三角形均是全等
的等边三角形,其中菱形AEFG可以看成是把菱形ABCD以点
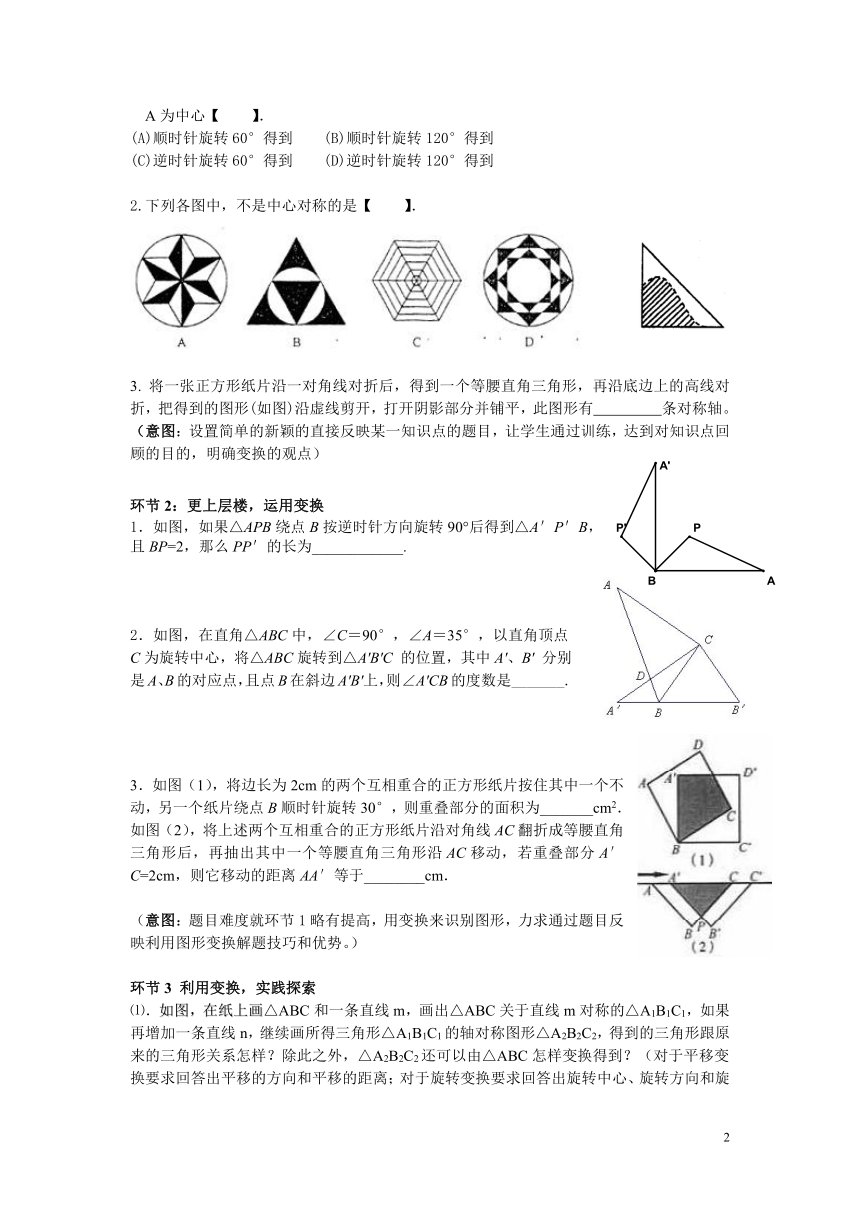
A为中心【 】.
(A)顺时针旋转60°得到 (B)顺时针旋转120°得到
(C)逆时针旋转60°得到 (D)逆时针旋转120°得到
2.下列各图中,不是中心对称的是【 】.
3. 将一张正方形纸片沿一对角线对折后,得到一个等腰直角三角形,再沿底边上的高线对折,把得到的图形(如图)沿虚线剪开,打开阴影部分并铺平,此图形有 条对称轴。
(意图:设置简单的新颖的直接反映某一知识点的题目,让学生通过训练,达到对知识点回顾的目的,明确变换的观点)
环节2:更上层楼,运用变换
1.如图,如果△APB绕点B按逆时针方向旋转90°后得到△A'P'B,且BP=2,那么PP'的长为____________.
2.如图,在直角△ABC中,∠C=90°,∠A=35°,以直角顶点C为旋转中心,将△ABC旋转到△A'B'C 的位置,其中A'、B' 分别是A、B的对应点,且点B在斜边A'B'上,则∠A'CB的度数是_______.
3.如图(1),将边长为2cm的两个互相重合的正方形纸片按住其中一个不动,另一个纸片绕点B顺时针旋转30°,则重叠部分的面积为_______cm2.
如图(2),将上述两个互相重合的正方形纸片沿对角线AC翻折成等腰直角三角形后,再抽出其中一个等腰直角三角形沿AC移动,若重叠部分A′C=2cm,则它移动的距离AA′等于________cm.
(意图:题目难度就环节1略有提高,用变换来识别图形,力求通过题目反映利用图形变换解题技巧和优势。)
环节3 利用变换,实践探索
⑴.如图,在纸上画△ABC和一条直线m,画出△ABC关于直线m对称的△A1B1C1,如果再增加一条直线n,继续画所得三角形△A1B1C1的轴对称图形△A2B2C2,得到的三角形跟原来的三角形关系怎样?除此之外,△A2B2C2还可以由△ABC怎样变换得到?(对于平移变换要求回答出平移的方向和平移的距离;对于旋转变换要求回答出旋转中心、旋转方向和旋转角度)学生可能不会回答旋转的情况,此时可提问:怎样构造直线n使得△A2B2C2可看成由 △ABC旋转得到?旋转的角度为多少?
①直线m与直线n平行时是什么情况?
②直线m与直线n不平行时是什么情况?
③直线m与直线n垂直呢?
⑵如图,四边形ABCD中,∠ADC=∠ABC=90°,AD=CD,DP⊥AB于P,若DP=5,则四边形ABCD的面积为 .
⑶.如图,正方形ABCD中,点P 是对角线BD上任意一点,过点P作PE⊥CD于E,PF⊥BC于F,连结EF,请问:EF与PA具有怎样的大小与位置关系?
(意图:经过环节1的基础训练和环节2的拓展训练后,本环节主要是通过实践探索发现平移、旋转和轴对称三种变换之间的联系,进一步强化平移、旋转和轴对称三种图形变换在解题中的应用。)
四、归纳小结
在图形的平移、旋转及轴对称作图中通过反映对应点的特征体现整个图形的特征。
平移的特征:①平移只改变图形的位置,不改变图形的形状与大小;
②对应线段平行(或在同一直线上)且相等;
③对应点的连线段平行(或在同一直线上)且相等。
旋转的特征:① (3)旋转的特征:①对应点到旋转中心的距离相等.
②图形上的每个点都绕旋转中心沿相同方向转动了同样的角度.(即任意一对对应点与旋转中心的连线所成的角都是旋转角)
③图形的形状、大小都不变对应线段相等,对应角相等.
轴对称的特征:①只改变图形的位置,不改变图形的形状与大小;
②对应点的连线被对称轴垂直平分。
五、课后作业
1.在梯形ABCD中,已知AB//CD,且AB+CD=5、AC=3、BD=4,则梯形ABCD的面积为 .
2、已知P是正方形ABCD内一点,PA=1、PB=3、PD=,求的大小
3、若由△ABC旋转得到△A/ B/ C/如图1所示,请做出它们的旋转中心.
A
B
C
O
D
E
PAGE
1
一、教学目标:
(1)能借助图形识别平移、旋转和轴对称三种基本变换的异同;
(2)能利用平移、旋转和轴对称三种变换认识基本图形并解决图形中的问题。
二、教学重点与难点
重点:利用变换认识图形的能力训练;
难点:应用变换找规律的能力训练。
三、教学过程:
1、借助图形,识别变换
如图,长方形ABCD中,对角线AC与BD
相交于O,DE∥AC,CE∥BD,那么△ABD
可以看作是由△__________旋转得到,旋转中心是_______,△DEC可以看作是由△__________经过 变换得到;有没有与△DEC成轴对称的三角形?中心对称呢?图中还有没有其它类似的图形变换?
通过回顾图形的三种变换,归纳总结如下
图形变换 共性 个性
轴对称 (1)形状不变、大小不变;(2)变换前后,两个图形全等,对应线段、对应角相等 对应点的连线段被对称轴垂直平分
平移 ①①对应线段平行(或在同一直线上)且相等;②对应点的连线段平行(或在同一直线上)且相等。
旋转 ①①对应点到旋转中心的距离相等. ②图形上的每个点都绕旋转中心沿相同方向转动了同样的角度.(即任意一对对应点与旋转中心的连线所成的角都是旋转角)
(意图:通过改编教材中的一道练习题,以题引入,借助图形帮助学生回顾图形的三种变换以及识别变换的异同)
2、训练与探索
环节1:动手练习,明确变换
1. 同学们曾玩过万花筒,它是由三块等宽等长的玻璃片围成的.
右图是看到的万花筒的一个图案,图中所有小三角形均是全等
的等边三角形,其中菱形AEFG可以看成是把菱形ABCD以点
A为中心【 】.
(A)顺时针旋转60°得到 (B)顺时针旋转120°得到
(C)逆时针旋转60°得到 (D)逆时针旋转120°得到
2.下列各图中,不是中心对称的是【 】.
3. 将一张正方形纸片沿一对角线对折后,得到一个等腰直角三角形,再沿底边上的高线对折,把得到的图形(如图)沿虚线剪开,打开阴影部分并铺平,此图形有 条对称轴。
(意图:设置简单的新颖的直接反映某一知识点的题目,让学生通过训练,达到对知识点回顾的目的,明确变换的观点)
环节2:更上层楼,运用变换
1.如图,如果△APB绕点B按逆时针方向旋转90°后得到△A'P'B,且BP=2,那么PP'的长为____________.
2.如图,在直角△ABC中,∠C=90°,∠A=35°,以直角顶点C为旋转中心,将△ABC旋转到△A'B'C 的位置,其中A'、B' 分别是A、B的对应点,且点B在斜边A'B'上,则∠A'CB的度数是_______.
3.如图(1),将边长为2cm的两个互相重合的正方形纸片按住其中一个不动,另一个纸片绕点B顺时针旋转30°,则重叠部分的面积为_______cm2.
如图(2),将上述两个互相重合的正方形纸片沿对角线AC翻折成等腰直角三角形后,再抽出其中一个等腰直角三角形沿AC移动,若重叠部分A′C=2cm,则它移动的距离AA′等于________cm.
(意图:题目难度就环节1略有提高,用变换来识别图形,力求通过题目反映利用图形变换解题技巧和优势。)
环节3 利用变换,实践探索
⑴.如图,在纸上画△ABC和一条直线m,画出△ABC关于直线m对称的△A1B1C1,如果再增加一条直线n,继续画所得三角形△A1B1C1的轴对称图形△A2B2C2,得到的三角形跟原来的三角形关系怎样?除此之外,△A2B2C2还可以由△ABC怎样变换得到?(对于平移变换要求回答出平移的方向和平移的距离;对于旋转变换要求回答出旋转中心、旋转方向和旋转角度)学生可能不会回答旋转的情况,此时可提问:怎样构造直线n使得△A2B2C2可看成由 △ABC旋转得到?旋转的角度为多少?
①直线m与直线n平行时是什么情况?
②直线m与直线n不平行时是什么情况?
③直线m与直线n垂直呢?
⑵如图,四边形ABCD中,∠ADC=∠ABC=90°,AD=CD,DP⊥AB于P,若DP=5,则四边形ABCD的面积为 .
⑶.如图,正方形ABCD中,点P 是对角线BD上任意一点,过点P作PE⊥CD于E,PF⊥BC于F,连结EF,请问:EF与PA具有怎样的大小与位置关系?
(意图:经过环节1的基础训练和环节2的拓展训练后,本环节主要是通过实践探索发现平移、旋转和轴对称三种变换之间的联系,进一步强化平移、旋转和轴对称三种图形变换在解题中的应用。)
四、归纳小结
在图形的平移、旋转及轴对称作图中通过反映对应点的特征体现整个图形的特征。
平移的特征:①平移只改变图形的位置,不改变图形的形状与大小;
②对应线段平行(或在同一直线上)且相等;
③对应点的连线段平行(或在同一直线上)且相等。
旋转的特征:① (3)旋转的特征:①对应点到旋转中心的距离相等.
②图形上的每个点都绕旋转中心沿相同方向转动了同样的角度.(即任意一对对应点与旋转中心的连线所成的角都是旋转角)
③图形的形状、大小都不变对应线段相等,对应角相等.
轴对称的特征:①只改变图形的位置,不改变图形的形状与大小;
②对应点的连线被对称轴垂直平分。
五、课后作业
1.在梯形ABCD中,已知AB//CD,且AB+CD=5、AC=3、BD=4,则梯形ABCD的面积为 .
2、已知P是正方形ABCD内一点,PA=1、PB=3、PD=,求的大小
3、若由△ABC旋转得到△A/ B/ C/如图1所示,请做出它们的旋转中心.
A
B
C
O
D
E
PAGE
1
同课章节目录
