人教版八年级上册数学14.3因式分解-十字相乘法 同步训练题(word版含简单答案)
文档属性
| 名称 | 人教版八年级上册数学14.3因式分解-十字相乘法 同步训练题(word版含简单答案) |  | |
| 格式 | doc | ||
| 文件大小 | 239.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-05 10:58:06 | ||
图片预览

文档简介
人教版八年级上册数学14.3十字相乘法因式分解训练题
一、单选题
1.因式分解m2-m-6正确的是( )
A.(m+2)(m-3) B.(m-2)(m+3) C.(m-2)(m-3) D.(m+2)(m+3)
2.如果多项式x2﹣5x+c可以用十字相乘法因式分解,那么下列c的取值正确的是( )
A.2 B.3 C.4 D.5
3.下列关于的二次三项式在实数范围内不能够因式分解的是( )
A.; B.; C.; D..
4.多项式的一个因式为( )
A. B. C. D.
5.若,则的值为( )
A. B. C. D.
6.若多项式可因式分解为,其中、、均为整数,则的值是( )
A.1 B.7 C.11 D.13
7.下列不可利用分解因式的是( )
A. B. C. D.
8.已知甲、乙、丙均为x的一次多项式,且其一次项的系数皆为正整数.若甲与乙相乘,积为,乙与丙相乘,积为,则甲与丙相加的结果是( )
A. B. C. D.
二、填空题
9.因式分解:
(1)___________;(2)___________;
(3)___________;(4)___________.
10.(________)(________);(________)(________);
(________)(________); (_______)(_______);
(______)(______); (______)(______).
11.若多项式可分解为.则的值为_____.
12.甲乙两人完成因式分解时,甲看错了a的值,分解的结果是,乙看错了b的值,分解的结果为,那么分解因式正确的结果为_________.
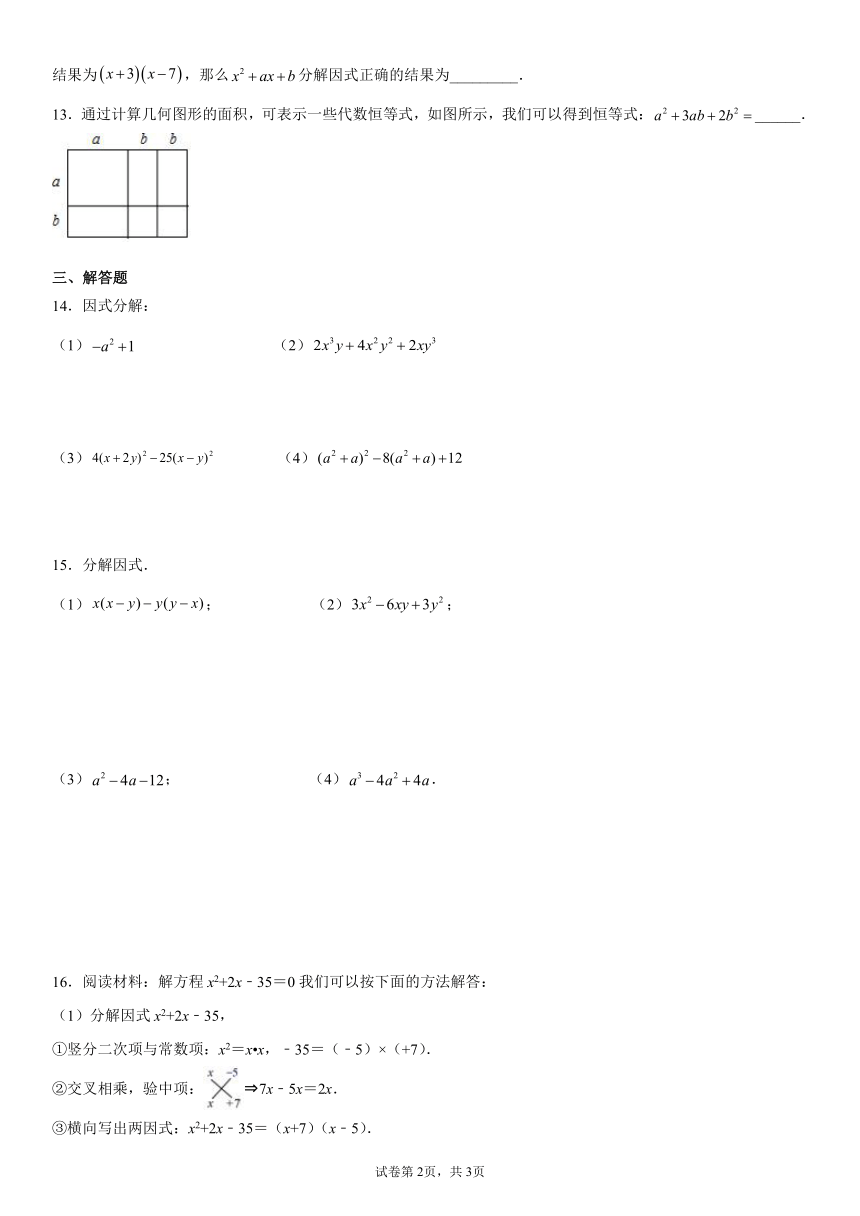
13.通过计算几何图形的面积,可表示一些代数恒等式,如图所示,我们可以得到恒等式:______.
三、解答题
14.因式分解:
(1) (2)
(3) (4)
15.分解因式.
(1); (2);
(3); (4).
16.阅读材料:解方程x2+2x﹣35=0我们可以按下面的方法解答:
(1)分解因式x2+2x﹣35,
①竖分二次项与常数项:x2=x x,﹣35=(﹣5)×(+7).
②交叉相乘,验中项: 7x﹣5x=2x.
③横向写出两因式:x2+2x﹣35=(x+7)(x﹣5).
(2)根据乘法原理:若ab=0,则a=0或b=0,则方程x2+2x﹣35=0可以这样求解x2+2x﹣35=0方程左边因式分解得(x+7)(x﹣5)=0所以原方程的解为x1=5,x2=﹣7
(3)试用上述方法和原理解下列方程:
①x2+5x+4=0;
②x2﹣6x﹣7=0;
③x2﹣6x+8=0;
④2x2+x﹣6=0.
参考答案
1.A
2.C
3.C
4.B
5.C
6.B
7.D
8.A
9.
10.
11.2
12.(x+2)(x-6)
13..
14.(1);(2);(3);(4)
15.(1)(x-y)(x+y);(2)3(x-y)2;(3)(a-6)(a+2);(4)a(a-2)2
16.①,;②,;③,;④,.
试卷第2页,共3页
试卷第3页,共3页
一、单选题
1.因式分解m2-m-6正确的是( )
A.(m+2)(m-3) B.(m-2)(m+3) C.(m-2)(m-3) D.(m+2)(m+3)
2.如果多项式x2﹣5x+c可以用十字相乘法因式分解,那么下列c的取值正确的是( )
A.2 B.3 C.4 D.5
3.下列关于的二次三项式在实数范围内不能够因式分解的是( )
A.; B.; C.; D..
4.多项式的一个因式为( )
A. B. C. D.
5.若,则的值为( )
A. B. C. D.
6.若多项式可因式分解为,其中、、均为整数,则的值是( )
A.1 B.7 C.11 D.13
7.下列不可利用分解因式的是( )
A. B. C. D.
8.已知甲、乙、丙均为x的一次多项式,且其一次项的系数皆为正整数.若甲与乙相乘,积为,乙与丙相乘,积为,则甲与丙相加的结果是( )
A. B. C. D.
二、填空题
9.因式分解:
(1)___________;(2)___________;
(3)___________;(4)___________.
10.(________)(________);(________)(________);
(________)(________); (_______)(_______);
(______)(______); (______)(______).
11.若多项式可分解为.则的值为_____.
12.甲乙两人完成因式分解时,甲看错了a的值,分解的结果是,乙看错了b的值,分解的结果为,那么分解因式正确的结果为_________.
13.通过计算几何图形的面积,可表示一些代数恒等式,如图所示,我们可以得到恒等式:______.
三、解答题
14.因式分解:
(1) (2)
(3) (4)
15.分解因式.
(1); (2);
(3); (4).
16.阅读材料:解方程x2+2x﹣35=0我们可以按下面的方法解答:
(1)分解因式x2+2x﹣35,
①竖分二次项与常数项:x2=x x,﹣35=(﹣5)×(+7).
②交叉相乘,验中项: 7x﹣5x=2x.
③横向写出两因式:x2+2x﹣35=(x+7)(x﹣5).
(2)根据乘法原理:若ab=0,则a=0或b=0,则方程x2+2x﹣35=0可以这样求解x2+2x﹣35=0方程左边因式分解得(x+7)(x﹣5)=0所以原方程的解为x1=5,x2=﹣7
(3)试用上述方法和原理解下列方程:
①x2+5x+4=0;
②x2﹣6x﹣7=0;
③x2﹣6x+8=0;
④2x2+x﹣6=0.
参考答案
1.A
2.C
3.C
4.B
5.C
6.B
7.D
8.A
9.
10.
11.2
12.(x+2)(x-6)
13..
14.(1);(2);(3);(4)
15.(1)(x-y)(x+y);(2)3(x-y)2;(3)(a-6)(a+2);(4)a(a-2)2
16.①,;②,;③,;④,.
试卷第2页,共3页
试卷第3页,共3页
