2021-2022学年高二上学期数学人教A版(2019)选择性必修第二4.1数列的概念训练题册(Word含解析)
文档属性
| 名称 | 2021-2022学年高二上学期数学人教A版(2019)选择性必修第二4.1数列的概念训练题册(Word含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 469.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-06 20:11:05 | ||
图片预览




文档简介
数列的概念训练题
一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知数列{an}的通项公式为an=(n+1),则该数列为( )
A.递增数列 B.递减数列
C.摇摆数列 D.先增后减数列
2.已知数列{an}的通项公式为an=n2﹣n,则可以作为这个数列的其中一项的数是( )
A.10 B.15 C.21 D.42
3.大衍数列,来源于《乾坤谱》中对易传“大衍之数五十”的推论,主要用于解释中国传统文化中的太极衍生原理,数列中的每一项都代表太极衍生过程,是中华传统文化中隐藏着的世界数学史上第一道数列题,其部分项如下:0,2,4,8,12,18,24,32,40,50,……,由此规律得到下列选项错误的是( )
A.a11=60 B.a12=72 C.a13=84 D.a14=94
4.猜想数列﹣,,﹣,, 的一个通项公式为an=( )
A. B.
C. D.
5.已知数列{an}的通项为an=n2+λn(n∈N*),则“a1<a2”是数列{an}递增的条件( )
A.充分非必要 B.必要非充分
C.充要条件 D.既非充分也非必要
6.数列,3,,,…,则是这个数列的第( )
A.8项 B.7项 C.6项 D.5项
7.已知数列{an}满足an=,且数列{an}是单调递增数列,则t的取值范围是( )
A.(,) B.(,+∞) C.(5,+∞) D.(1,4]
8.已知数列{an}的通项公式为,a5是数列{an}的最小项,则实数a的取值范围是( )
A.[﹣40,﹣25] B.[﹣40,0] C.[﹣25,25] D.[﹣25,0]
二、选择题:本题共4小题,每小题5分,共20分。在每小题给出的选项中,有多项符合题目要求。全部选对的得5分,部分选对的得2分,有选错的得0分。
9.下列四个选项中,正确的是( )
A.数列的图象是一群孤立的点
B.数列1,﹣1,1,﹣1,…与数列﹣1,1,﹣1,1,…是同一数列
C.数列,,,,…的一个通项公式是an=(n∈N*)
D.数列,…,是递减数列
10.若数列{an}的前4项依次为2,0,2,0,则数列{an}的通项公式可能是( )
A. B.
C. D.
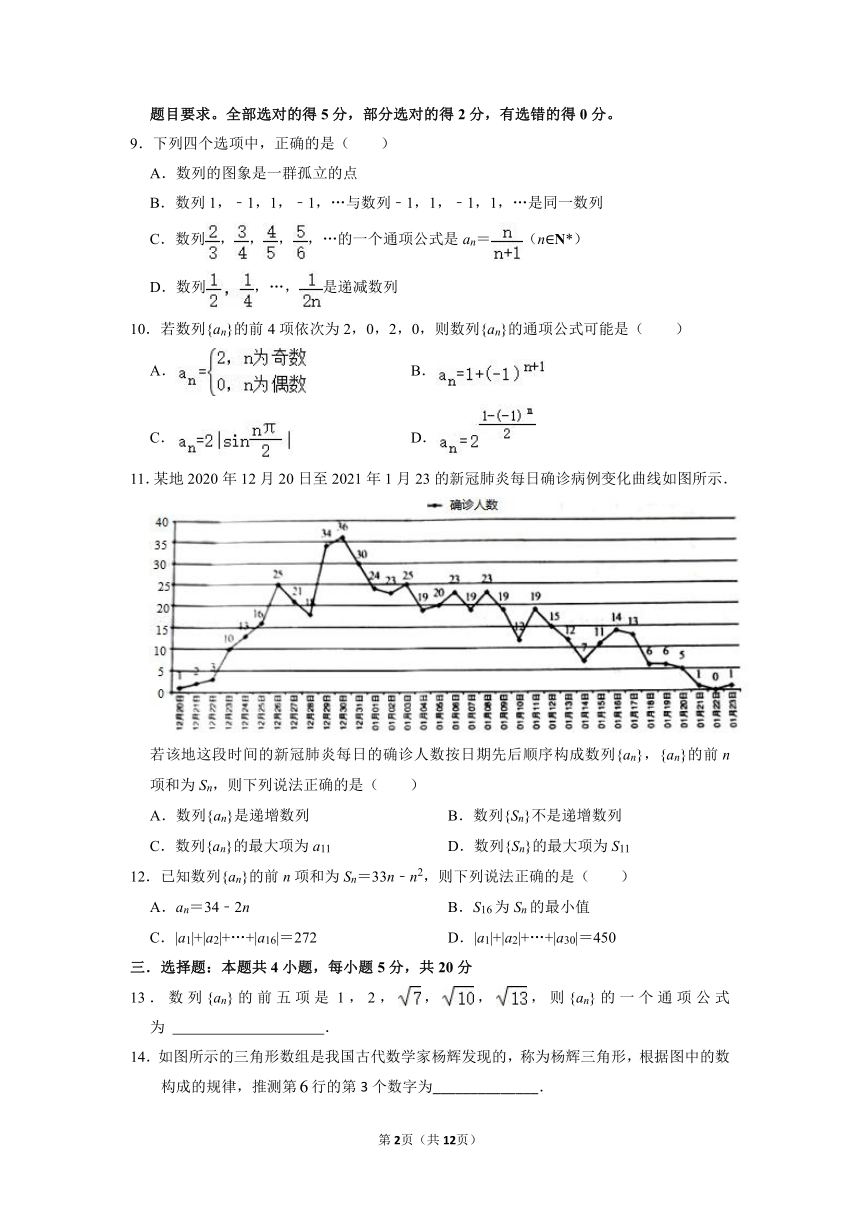
11.某地2020年12月20日至2021年1月23的新冠肺炎每日确诊病例变化曲线如图所示.
若该地这段时间的新冠肺炎每日的确诊人数按日期先后顺序构成数列{an},{an}的前n项和为Sn,则下列说法正确的是( )
A.数列{an}是递增数列 B.数列{Sn}不是递增数列
C.数列{an}的最大项为a11 D.数列{Sn}的最大项为S11
12.已知数列{an}的前n项和为Sn=33n﹣n2,则下列说法正确的是( )
A.an=34﹣2n B.S16为Sn的最小值
C.|a1|+|a2|+…+|a16|=272 D.|a1|+|a2|+…+|a30|=450
三.选择题:本题共4小题,每小题5分,共20分
13.数列{an}的前五项是1,2,,,,则{an}的一个通项公式为 .
14.如图所示的三角形数组是我国古代数学家杨辉发现的,称为杨辉三角形,根据图中的数构成的规律,推测第行的第3个数字为______________.
15.在数列{an}中,对任意n∈N*,an=k,当且仅当2k≤n<2k+1,k∈N,若满足am+a2m+a4m+a8m+a16m≥52,则m的最小值为 .
16.已知集合A={m|m=x2﹣y2,x、y∈Z},将A中的正整数从小到大排列为:a1,a2,a3,….若an=2015,则正整数n= .
四、解答题:本题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤。
17.根据下面数列的前几项,写出数列的一个通项公式:
(1),,,,,…;
(2)0,2,0,2,0,2,…;
(3)1,3,3,5,5,7,7,9,9,…;
18.已知数列{an}的通项公式为an=.
(1)求这个数列的第10项;
(2)在区间()内是否存在数列中的项?若有,有几项?若没有,说明理由.
19.已知数列{an}满足an=n2﹣5n﹣6,n∈N+
(Ⅰ)数列中有哪些项是负数?
(Ⅱ)当n为何值时,an取得最小值?并求出此最小值.
20.已知数列{an}的前n项和为Sn,且Sn=2n2﹣30n.
(1)求出它的通项公式;
(2)求使得Sn最小的序号n的值.
21.已知数列{an}满足:a1=m(m为正整数),an+1=若a4=4,求m所有可能的取值.
22.已知常数a≠0,数列{an}的前n项和为Sn,a1=1,an=+a(n﹣1).
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若bn=3n+(﹣1)nan,且{bn}是单调递增数列,求实数a的取值范围;
(Ⅲ)若a=,cn=,对于任意给定的正整数k,是否存在正整数p、q,使得ck=cpcq,?若存在,求出p、q的值(只要写出一组即可);若不存在,请说明理由.
数列的概念训练题
一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知数列{an}的通项公式为an=(n+1),则该数列为( )
A.递增数列 B.递减数列
C.摇摆数列 D.先增后减数列
【解答】解:an=(n+1),
则an+1﹣an=(n+2)()n+1﹣(n+1)=()()n,
易知0<()n<1,
所以当n≤9时,an+1﹣an≥0,n>9时,an+1﹣an<0,
故该数列为先增后减数列.
故选:D.
2.已知数列{an}的通项公式为an=n2﹣n,则可以作为这个数列的其中一项的数是( )
A.10 B.15 C.21 D.42
【解答】解:根据题意,依次分析选项:
对于A,若an=n2﹣n=n(n﹣1)=10,无正整数解,不是数列中的项;
对于B,若an=n2﹣n=n(n﹣1)=15,无正整数解,不是数列中的项;
对于C,若an=n2﹣n=n(n﹣1)=21,无正整数解,不是数列中的项;
对于D,若an=n2﹣n=n(n﹣1)=42,有正整数解n=7,则42是数列中的项;
故选:D.
3.大衍数列,来源于《乾坤谱》中对易传“大衍之数五十”的推论,主要用于解释中国传统文化中的太极衍生原理,数列中的每一项都代表太极衍生过程,是中华传统文化中隐藏着的世界数学史上第一道数列题,其部分项如下:0,2,4,8,12,18,24,32,40,50,……,由此规律得到下列选项错误的是( )
A.a11=60 B.a12=72 C.a13=84 D.a14=94
【解答】解:根据题意,数列0,2,4,8,12,18,24,32,40,50,……,
其通项公式可以为an=,
则a11=60,a12=72,a13=84,a14=98,
故选:D.
4.猜想数列﹣,,﹣,, 的一个通项公式为an=( )
A. B.
C. D.
【解答】解:∵数列﹣,,﹣,,
每一项的分母为项数的2倍加1,即2n+1,
每一项的分子为3的项数次方减1,即3n﹣1,
符号为﹣1的项数次方,即(﹣1)n,
故猜想该数列的一个通项公式为an=.
故选:D.
5.已知数列{an}的通项为an=n2+λn(n∈N*),则“a1<a2”是数列{an}递增的条件( )
A.充分非必要 B.必要非充分
C.充要条件 D.既非充分也非必要
【解答】解:a1<a2 1+λ<4+2λ λ>﹣3,
数列{an}递增 an+1﹣an>0恒成立 λ>﹣(2n+1) λ>﹣3.
因此“a1<a2”是数列{an}递增的充要条件.
故选:C.
6.数列,3,,,…,则是这个数列的第( )
A.8项 B.7项 C.6项 D.5项
【解答】解:由=,3=,,,…,则第n项,
∴为第第7项.
故选:B.
7.已知数列{an}满足an=,且数列{an}是单调递增数列,则t的取值范围是( )
A.(,) B.(,+∞) C.(5,+∞) D.(1,4]
【解答】解:∵数列{an}满足an=,且数列{an}是单调递增数列,
∴,求得<t<,
故选:A.
8.已知数列{an}的通项公式为,a5是数列{an}的最小项,则实数a的取值范围是( )
A.[﹣40,﹣25] B.[﹣40,0] C.[﹣25,25] D.[﹣25,0]
【解答】解:由条件有对任意的n∈N*,由an≥a5恒成立,即,整理得.
当n≤4时,不等式化简为a≥5n(n﹣6)恒成立,所以a≥﹣25;
当n≥6时,不等式化简为a≤5n(n﹣6)恒成立,所以a≤0;
综上:﹣25≤a≤0.
故选:D.
二、选择题:本题共4小题,每小题5分,共20分。在每小题给出的选项中,有多项符合题目要求。全部选对的得5分,部分选对的得2分,有选错的得0分。
9.下列四个选项中,正确的是( )
A.数列的图象是一群孤立的点
B.数列1,﹣1,1,﹣1,…与数列﹣1,1,﹣1,1,…是同一数列
C.数列,,,,…的一个通项公式是an=(n∈N*)
D.数列,…,是递减数列
【解答】解:对于A,由数列的通项公式以及n∈N*可知,数列的图象是一群孤立的点,故选项A正确;
对于B,由于两个数列中的数排列的次序不同,因此不是同一数列,故选项B错误;
对于C,an=,a1=≠,不符合题意,故选项C错误;
对于D,数列,…,递减数列,故选项D正确.
故选:AD.
10.若数列{an}的前4项依次为2,0,2,0,则数列{an}的通项公式可能是( )
A. B.
C. D.
【解答】解:根据题意,依次分析选项:
对于A,该数列的前4项为2,0,2,0,符合题意;
对于B,该数列的前4项为2,0,2,0,符合题意;
对于C,an=2|sin|,该数列的前4项为2,0,2,0,符合题意;
对于D,该数列的前4项为2,1,2,1,不符合题意;
故选:ABC.
11.某地2020年12月20日至2021年1月23的新冠肺炎每日确诊病例变化曲线如图所示.
若该地这段时间的新冠肺炎每日的确诊人数按日期先后顺序构成数列{an},{an}的前n项和为Sn,则下列说法正确的是( )
A.数列{an}是递增数列 B.数列{Sn}不是递增数列
C.数列{an}的最大项为a11 D.数列{Sn}的最大项为S11
【解答】解:因为12月27日新增确诊人数小于12月26日新增确证人数,即a7>a8,
所以{an}不是递增数列,所以A错误;
因为1月22日新增确诊病例为0,即S33=S34,
所以{Sn}不是递增数列,所以B正确;
因为12月31日新增确诊病例最多,从12月20日算起,12月31日是第11天,
所以数列{an}的最大项是a11,所以C选项正确,
数列{Sn}的最大项是最后一项,所以选项D错误,
故选:BC.
12.已知数列{an}的前n项和为Sn=33n﹣n2,则下列说法正确的是( )
A.an=34﹣2n B.S16为Sn的最小值
C.|a1|+|a2|+…+|a16|=272 D.|a1|+|a2|+…+|a30|=450
【解答】解:数列{an}的前n项和为Sn=33n﹣n2,
当n=1时,a1=32,
当n≥2时,an=Sn﹣Sn﹣1=33n﹣n2﹣33(n﹣1)+(n﹣1)2=﹣2n+34,
当n=1时也成立,
∴an=34﹣2n,故A正确;
由于Sn=33n﹣n2=﹣(n﹣)2+,当n=16或17时,Sn取得最大值,故B错误;
由于an=﹣2n+34≥0,解得n≤17,
∴|a1|+|a2|+…+|a16|=a1+a2+a3+…+a16==272,故C正确;
∴|a1|+|a2|+…+|a30|=a1+…+a16﹣(a17+a18+…+a30)=272﹣=454,故D错误.
故选:AC.
三.选择题:本题共4小题,每小题5分,共20分
13.数列{an}的前五项是1,2,,,,则{an}的一个通项公式为 an= .
【解答】解:根据题意,对于数列{an},a1==1,
a2===2,
a3==,
a4==,
……
故an=,
故答案为:an=.
14.如图所示的三角形数组是我国古代数学家杨辉发现的,称为杨辉三角形,根据图中的数构成的规律,推测第行的第3个数字为______________.
【解答】由题图可知,从第3行开始,每个数字都等于其“肩上”的两数之和,那么第行的数字为,故第3个数字为.
15.在数列{an}中,对任意n∈N*,an=k,当且仅当2k≤n<2k+1,k∈N,若满足am+a2m+a4m+a8m+a16m≥52,则m的最小值为 512 .
【解答】解:不妨设2k≤m<2k+1,k∈N*,m∈N*,
由题意可得,am=k,
因为2k+1≤2m<2k+2,
所以a2m=k+1,
同理可得,a4m=k+2,a8m=k+3,a16m=k+4,…
所以am+a2m+a4m+a8m+a16m=k+(k+1)+(k+2)+(k+3)+(k+4)=5k+10,
因为am+a2m+a4m+a8m+a16m≥52,
所以5k+10≥52,
解得,又k∈N*,
所以k的最小值整数解为9,
故m的最小值为29=512.
故答案为:512.
16.已知集合A={m|m=x2﹣y2,x、y∈Z},将A中的正整数从小到大排列为:a1,a2,a3,….若an=2015,则正整数n= 1511 .
【解答】解:m=x2﹣y2=(x﹣y)(x+y),
当x﹣y=1时,即m=x+y=y+1+y=2y+1(表示奇数),
当x﹣y=2时,即m=2x+2y=2×(y+2)+2y=4y+4(表示4的倍数),
∴将A中的正整数从小到大排列为,可得1,3,4,5,7,8, 即每4个正数,保留3个,不取第二个数,
∵2015÷4=503 3,
∴n=503×3+2=1511.
故答案为:1511.
四、解答题:本题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤。
17.根据下面数列的前几项,写出数列的一个通项公式:
(1),,,,,…;
(2)0,2,0,2,0,2,…;
(3)1,3,3,5,5,7,7,9,9,…;
【解析】(1)分子是连续的正偶数,分母为分子的平方减去1,它的一个通项公式为an=;
(2)将数列变形为,…,易知它的一个通项公式为an=;
(3)将数列变形为1+0,2+1,3+0,4+1,5+0,6+1,7+0,8+1,…,类似于(3)可得它的一个通项公式为an=n+;
18.已知数列{an}的通项公式为an=.
(1)求这个数列的第10项;
(2)在区间()内是否存在数列中的项?若有,有几项?若没有,说明理由.
【解答】解:(1)根据题意,数列{an}的通项公式为an=,
则a10==;
(2)根据题意,<<,解可得:<n<,
又由n为正整数,则n=2,
则在区间()内只存在数列的一项.
19.已知数列{an}满足an=n2﹣5n﹣6,n∈N+
(Ⅰ)数列中有哪些项是负数?
(Ⅱ)当n为何值时,an取得最小值?并求出此最小值.
【解答】解:(Ⅰ)an=n2﹣5n﹣6<0,解得0<n<6,
∵n∈N+,
∴数列中第1,2,3,4,5项为负数,即﹣10,﹣12,﹣12,﹣10,﹣6,
(Ⅱ)an=n2﹣5n﹣6=(n﹣)2﹣,当n=2,3时an取得最小值,最小值为﹣12.
20.已知数列{an}的前n项和为Sn,且Sn=2n2﹣30n.
(1)求出它的通项公式;
(2)求使得Sn最小的序号n的值.
【解答】解:(1)当n=1时,a1=S1=2﹣30=﹣28;
当n≥2时,an=Sn﹣Sn﹣1=2n2﹣30n﹣[2(n﹣1)2﹣30(n﹣1)]=4n﹣32.
当n=1时,上式成立.
∴an=4n﹣32.
(2)Sn=2n2﹣30n=.
∴当n=7或8时,Sn取得最小值.
21.已知数列{an}满足:a1=m(m为正整数),an+1=若a4=4,求m所有可能的取值.
【解答】若a3为奇数,则3a3+1=4,a3=1,若a2为奇数,则3a2+1=1,a2=0(舍去),若a2为偶数,则=1,a2=2.
若a1为奇数,则3a1+1=2,a1=(舍去),
若a1为偶数,=2,a1=4;
若a3为偶数,则=4,a3=8,
若a2为奇数,则3a2+1=8,a2=(舍去).
若a2为偶数,则=8,a2=16.
若a1为奇数,则3a1+1=16,a1=5.
若a1为偶数,则=16,a1=32.
故m所有可能的取值为4,5,32.
22.已知常数a≠0,数列{an}的前n项和为Sn,a1=1,an=+a(n﹣1).
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若bn=3n+(﹣1)nan,且{bn}是单调递增数列,求实数a的取值范围;
(Ⅲ)若a=,cn=,对于任意给定的正整数k,是否存在正整数p、q,使得ck=cpcq,?若存在,求出p、q的值(只要写出一组即可);若不存在,请说明理由.
【解答】解:(Ⅰ),
.
∴{an}是以a1=1为首项,d=2a为公差的等差数列,
∴an=1+2a(n﹣1);
(Ⅱ),即(﹣1)n[1+a(2n﹣1)]<3n
若n为奇数,则恒成立,
考察,
即f(1)>f(3)>f(5)>…,∴a>f(1)=﹣4;
若n为偶数,则恒成立,
考察,
即g(2)<g(4)<g(6)<…,
∴;综上所述,;
(Ⅲ)由(1).假设对任意k∈N*,总存在正整数p、q,使ck=cpcq,
则
令q=k+1,则p=k(k+2017)(或q=2k,则p=2k+2016;…)
∴ck=ck(k+2017)ck+1(或ck=c2k+2016c2k;…).
第1页(共3页)
一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知数列{an}的通项公式为an=(n+1),则该数列为( )
A.递增数列 B.递减数列
C.摇摆数列 D.先增后减数列
2.已知数列{an}的通项公式为an=n2﹣n,则可以作为这个数列的其中一项的数是( )
A.10 B.15 C.21 D.42
3.大衍数列,来源于《乾坤谱》中对易传“大衍之数五十”的推论,主要用于解释中国传统文化中的太极衍生原理,数列中的每一项都代表太极衍生过程,是中华传统文化中隐藏着的世界数学史上第一道数列题,其部分项如下:0,2,4,8,12,18,24,32,40,50,……,由此规律得到下列选项错误的是( )
A.a11=60 B.a12=72 C.a13=84 D.a14=94
4.猜想数列﹣,,﹣,, 的一个通项公式为an=( )
A. B.
C. D.
5.已知数列{an}的通项为an=n2+λn(n∈N*),则“a1<a2”是数列{an}递增的条件( )
A.充分非必要 B.必要非充分
C.充要条件 D.既非充分也非必要
6.数列,3,,,…,则是这个数列的第( )
A.8项 B.7项 C.6项 D.5项
7.已知数列{an}满足an=,且数列{an}是单调递增数列,则t的取值范围是( )
A.(,) B.(,+∞) C.(5,+∞) D.(1,4]
8.已知数列{an}的通项公式为,a5是数列{an}的最小项,则实数a的取值范围是( )
A.[﹣40,﹣25] B.[﹣40,0] C.[﹣25,25] D.[﹣25,0]
二、选择题:本题共4小题,每小题5分,共20分。在每小题给出的选项中,有多项符合题目要求。全部选对的得5分,部分选对的得2分,有选错的得0分。
9.下列四个选项中,正确的是( )
A.数列的图象是一群孤立的点
B.数列1,﹣1,1,﹣1,…与数列﹣1,1,﹣1,1,…是同一数列
C.数列,,,,…的一个通项公式是an=(n∈N*)
D.数列,…,是递减数列
10.若数列{an}的前4项依次为2,0,2,0,则数列{an}的通项公式可能是( )
A. B.
C. D.
11.某地2020年12月20日至2021年1月23的新冠肺炎每日确诊病例变化曲线如图所示.
若该地这段时间的新冠肺炎每日的确诊人数按日期先后顺序构成数列{an},{an}的前n项和为Sn,则下列说法正确的是( )
A.数列{an}是递增数列 B.数列{Sn}不是递增数列
C.数列{an}的最大项为a11 D.数列{Sn}的最大项为S11
12.已知数列{an}的前n项和为Sn=33n﹣n2,则下列说法正确的是( )
A.an=34﹣2n B.S16为Sn的最小值
C.|a1|+|a2|+…+|a16|=272 D.|a1|+|a2|+…+|a30|=450
三.选择题:本题共4小题,每小题5分,共20分
13.数列{an}的前五项是1,2,,,,则{an}的一个通项公式为 .
14.如图所示的三角形数组是我国古代数学家杨辉发现的,称为杨辉三角形,根据图中的数构成的规律,推测第行的第3个数字为______________.
15.在数列{an}中,对任意n∈N*,an=k,当且仅当2k≤n<2k+1,k∈N,若满足am+a2m+a4m+a8m+a16m≥52,则m的最小值为 .
16.已知集合A={m|m=x2﹣y2,x、y∈Z},将A中的正整数从小到大排列为:a1,a2,a3,….若an=2015,则正整数n= .
四、解答题:本题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤。
17.根据下面数列的前几项,写出数列的一个通项公式:
(1),,,,,…;
(2)0,2,0,2,0,2,…;
(3)1,3,3,5,5,7,7,9,9,…;
18.已知数列{an}的通项公式为an=.
(1)求这个数列的第10项;
(2)在区间()内是否存在数列中的项?若有,有几项?若没有,说明理由.
19.已知数列{an}满足an=n2﹣5n﹣6,n∈N+
(Ⅰ)数列中有哪些项是负数?
(Ⅱ)当n为何值时,an取得最小值?并求出此最小值.
20.已知数列{an}的前n项和为Sn,且Sn=2n2﹣30n.
(1)求出它的通项公式;
(2)求使得Sn最小的序号n的值.
21.已知数列{an}满足:a1=m(m为正整数),an+1=若a4=4,求m所有可能的取值.
22.已知常数a≠0,数列{an}的前n项和为Sn,a1=1,an=+a(n﹣1).
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若bn=3n+(﹣1)nan,且{bn}是单调递增数列,求实数a的取值范围;
(Ⅲ)若a=,cn=,对于任意给定的正整数k,是否存在正整数p、q,使得ck=cpcq,?若存在,求出p、q的值(只要写出一组即可);若不存在,请说明理由.
数列的概念训练题
一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知数列{an}的通项公式为an=(n+1),则该数列为( )
A.递增数列 B.递减数列
C.摇摆数列 D.先增后减数列
【解答】解:an=(n+1),
则an+1﹣an=(n+2)()n+1﹣(n+1)=()()n,
易知0<()n<1,
所以当n≤9时,an+1﹣an≥0,n>9时,an+1﹣an<0,
故该数列为先增后减数列.
故选:D.
2.已知数列{an}的通项公式为an=n2﹣n,则可以作为这个数列的其中一项的数是( )
A.10 B.15 C.21 D.42
【解答】解:根据题意,依次分析选项:
对于A,若an=n2﹣n=n(n﹣1)=10,无正整数解,不是数列中的项;
对于B,若an=n2﹣n=n(n﹣1)=15,无正整数解,不是数列中的项;
对于C,若an=n2﹣n=n(n﹣1)=21,无正整数解,不是数列中的项;
对于D,若an=n2﹣n=n(n﹣1)=42,有正整数解n=7,则42是数列中的项;
故选:D.
3.大衍数列,来源于《乾坤谱》中对易传“大衍之数五十”的推论,主要用于解释中国传统文化中的太极衍生原理,数列中的每一项都代表太极衍生过程,是中华传统文化中隐藏着的世界数学史上第一道数列题,其部分项如下:0,2,4,8,12,18,24,32,40,50,……,由此规律得到下列选项错误的是( )
A.a11=60 B.a12=72 C.a13=84 D.a14=94
【解答】解:根据题意,数列0,2,4,8,12,18,24,32,40,50,……,
其通项公式可以为an=,
则a11=60,a12=72,a13=84,a14=98,
故选:D.
4.猜想数列﹣,,﹣,, 的一个通项公式为an=( )
A. B.
C. D.
【解答】解:∵数列﹣,,﹣,,
每一项的分母为项数的2倍加1,即2n+1,
每一项的分子为3的项数次方减1,即3n﹣1,
符号为﹣1的项数次方,即(﹣1)n,
故猜想该数列的一个通项公式为an=.
故选:D.
5.已知数列{an}的通项为an=n2+λn(n∈N*),则“a1<a2”是数列{an}递增的条件( )
A.充分非必要 B.必要非充分
C.充要条件 D.既非充分也非必要
【解答】解:a1<a2 1+λ<4+2λ λ>﹣3,
数列{an}递增 an+1﹣an>0恒成立 λ>﹣(2n+1) λ>﹣3.
因此“a1<a2”是数列{an}递增的充要条件.
故选:C.
6.数列,3,,,…,则是这个数列的第( )
A.8项 B.7项 C.6项 D.5项
【解答】解:由=,3=,,,…,则第n项,
∴为第第7项.
故选:B.
7.已知数列{an}满足an=,且数列{an}是单调递增数列,则t的取值范围是( )
A.(,) B.(,+∞) C.(5,+∞) D.(1,4]
【解答】解:∵数列{an}满足an=,且数列{an}是单调递增数列,
∴,求得<t<,
故选:A.
8.已知数列{an}的通项公式为,a5是数列{an}的最小项,则实数a的取值范围是( )
A.[﹣40,﹣25] B.[﹣40,0] C.[﹣25,25] D.[﹣25,0]
【解答】解:由条件有对任意的n∈N*,由an≥a5恒成立,即,整理得.
当n≤4时,不等式化简为a≥5n(n﹣6)恒成立,所以a≥﹣25;
当n≥6时,不等式化简为a≤5n(n﹣6)恒成立,所以a≤0;
综上:﹣25≤a≤0.
故选:D.
二、选择题:本题共4小题,每小题5分,共20分。在每小题给出的选项中,有多项符合题目要求。全部选对的得5分,部分选对的得2分,有选错的得0分。
9.下列四个选项中,正确的是( )
A.数列的图象是一群孤立的点
B.数列1,﹣1,1,﹣1,…与数列﹣1,1,﹣1,1,…是同一数列
C.数列,,,,…的一个通项公式是an=(n∈N*)
D.数列,…,是递减数列
【解答】解:对于A,由数列的通项公式以及n∈N*可知,数列的图象是一群孤立的点,故选项A正确;
对于B,由于两个数列中的数排列的次序不同,因此不是同一数列,故选项B错误;
对于C,an=,a1=≠,不符合题意,故选项C错误;
对于D,数列,…,递减数列,故选项D正确.
故选:AD.
10.若数列{an}的前4项依次为2,0,2,0,则数列{an}的通项公式可能是( )
A. B.
C. D.
【解答】解:根据题意,依次分析选项:
对于A,该数列的前4项为2,0,2,0,符合题意;
对于B,该数列的前4项为2,0,2,0,符合题意;
对于C,an=2|sin|,该数列的前4项为2,0,2,0,符合题意;
对于D,该数列的前4项为2,1,2,1,不符合题意;
故选:ABC.
11.某地2020年12月20日至2021年1月23的新冠肺炎每日确诊病例变化曲线如图所示.
若该地这段时间的新冠肺炎每日的确诊人数按日期先后顺序构成数列{an},{an}的前n项和为Sn,则下列说法正确的是( )
A.数列{an}是递增数列 B.数列{Sn}不是递增数列
C.数列{an}的最大项为a11 D.数列{Sn}的最大项为S11
【解答】解:因为12月27日新增确诊人数小于12月26日新增确证人数,即a7>a8,
所以{an}不是递增数列,所以A错误;
因为1月22日新增确诊病例为0,即S33=S34,
所以{Sn}不是递增数列,所以B正确;
因为12月31日新增确诊病例最多,从12月20日算起,12月31日是第11天,
所以数列{an}的最大项是a11,所以C选项正确,
数列{Sn}的最大项是最后一项,所以选项D错误,
故选:BC.
12.已知数列{an}的前n项和为Sn=33n﹣n2,则下列说法正确的是( )
A.an=34﹣2n B.S16为Sn的最小值
C.|a1|+|a2|+…+|a16|=272 D.|a1|+|a2|+…+|a30|=450
【解答】解:数列{an}的前n项和为Sn=33n﹣n2,
当n=1时,a1=32,
当n≥2时,an=Sn﹣Sn﹣1=33n﹣n2﹣33(n﹣1)+(n﹣1)2=﹣2n+34,
当n=1时也成立,
∴an=34﹣2n,故A正确;
由于Sn=33n﹣n2=﹣(n﹣)2+,当n=16或17时,Sn取得最大值,故B错误;
由于an=﹣2n+34≥0,解得n≤17,
∴|a1|+|a2|+…+|a16|=a1+a2+a3+…+a16==272,故C正确;
∴|a1|+|a2|+…+|a30|=a1+…+a16﹣(a17+a18+…+a30)=272﹣=454,故D错误.
故选:AC.
三.选择题:本题共4小题,每小题5分,共20分
13.数列{an}的前五项是1,2,,,,则{an}的一个通项公式为 an= .
【解答】解:根据题意,对于数列{an},a1==1,
a2===2,
a3==,
a4==,
……
故an=,
故答案为:an=.
14.如图所示的三角形数组是我国古代数学家杨辉发现的,称为杨辉三角形,根据图中的数构成的规律,推测第行的第3个数字为______________.
【解答】由题图可知,从第3行开始,每个数字都等于其“肩上”的两数之和,那么第行的数字为,故第3个数字为.
15.在数列{an}中,对任意n∈N*,an=k,当且仅当2k≤n<2k+1,k∈N,若满足am+a2m+a4m+a8m+a16m≥52,则m的最小值为 512 .
【解答】解:不妨设2k≤m<2k+1,k∈N*,m∈N*,
由题意可得,am=k,
因为2k+1≤2m<2k+2,
所以a2m=k+1,
同理可得,a4m=k+2,a8m=k+3,a16m=k+4,…
所以am+a2m+a4m+a8m+a16m=k+(k+1)+(k+2)+(k+3)+(k+4)=5k+10,
因为am+a2m+a4m+a8m+a16m≥52,
所以5k+10≥52,
解得,又k∈N*,
所以k的最小值整数解为9,
故m的最小值为29=512.
故答案为:512.
16.已知集合A={m|m=x2﹣y2,x、y∈Z},将A中的正整数从小到大排列为:a1,a2,a3,….若an=2015,则正整数n= 1511 .
【解答】解:m=x2﹣y2=(x﹣y)(x+y),
当x﹣y=1时,即m=x+y=y+1+y=2y+1(表示奇数),
当x﹣y=2时,即m=2x+2y=2×(y+2)+2y=4y+4(表示4的倍数),
∴将A中的正整数从小到大排列为,可得1,3,4,5,7,8, 即每4个正数,保留3个,不取第二个数,
∵2015÷4=503 3,
∴n=503×3+2=1511.
故答案为:1511.
四、解答题:本题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤。
17.根据下面数列的前几项,写出数列的一个通项公式:
(1),,,,,…;
(2)0,2,0,2,0,2,…;
(3)1,3,3,5,5,7,7,9,9,…;
【解析】(1)分子是连续的正偶数,分母为分子的平方减去1,它的一个通项公式为an=;
(2)将数列变形为,…,易知它的一个通项公式为an=;
(3)将数列变形为1+0,2+1,3+0,4+1,5+0,6+1,7+0,8+1,…,类似于(3)可得它的一个通项公式为an=n+;
18.已知数列{an}的通项公式为an=.
(1)求这个数列的第10项;
(2)在区间()内是否存在数列中的项?若有,有几项?若没有,说明理由.
【解答】解:(1)根据题意,数列{an}的通项公式为an=,
则a10==;
(2)根据题意,<<,解可得:<n<,
又由n为正整数,则n=2,
则在区间()内只存在数列的一项.
19.已知数列{an}满足an=n2﹣5n﹣6,n∈N+
(Ⅰ)数列中有哪些项是负数?
(Ⅱ)当n为何值时,an取得最小值?并求出此最小值.
【解答】解:(Ⅰ)an=n2﹣5n﹣6<0,解得0<n<6,
∵n∈N+,
∴数列中第1,2,3,4,5项为负数,即﹣10,﹣12,﹣12,﹣10,﹣6,
(Ⅱ)an=n2﹣5n﹣6=(n﹣)2﹣,当n=2,3时an取得最小值,最小值为﹣12.
20.已知数列{an}的前n项和为Sn,且Sn=2n2﹣30n.
(1)求出它的通项公式;
(2)求使得Sn最小的序号n的值.
【解答】解:(1)当n=1时,a1=S1=2﹣30=﹣28;
当n≥2时,an=Sn﹣Sn﹣1=2n2﹣30n﹣[2(n﹣1)2﹣30(n﹣1)]=4n﹣32.
当n=1时,上式成立.
∴an=4n﹣32.
(2)Sn=2n2﹣30n=.
∴当n=7或8时,Sn取得最小值.
21.已知数列{an}满足:a1=m(m为正整数),an+1=若a4=4,求m所有可能的取值.
【解答】若a3为奇数,则3a3+1=4,a3=1,若a2为奇数,则3a2+1=1,a2=0(舍去),若a2为偶数,则=1,a2=2.
若a1为奇数,则3a1+1=2,a1=(舍去),
若a1为偶数,=2,a1=4;
若a3为偶数,则=4,a3=8,
若a2为奇数,则3a2+1=8,a2=(舍去).
若a2为偶数,则=8,a2=16.
若a1为奇数,则3a1+1=16,a1=5.
若a1为偶数,则=16,a1=32.
故m所有可能的取值为4,5,32.
22.已知常数a≠0,数列{an}的前n项和为Sn,a1=1,an=+a(n﹣1).
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若bn=3n+(﹣1)nan,且{bn}是单调递增数列,求实数a的取值范围;
(Ⅲ)若a=,cn=,对于任意给定的正整数k,是否存在正整数p、q,使得ck=cpcq,?若存在,求出p、q的值(只要写出一组即可);若不存在,请说明理由.
【解答】解:(Ⅰ),
.
∴{an}是以a1=1为首项,d=2a为公差的等差数列,
∴an=1+2a(n﹣1);
(Ⅱ),即(﹣1)n[1+a(2n﹣1)]<3n
若n为奇数,则恒成立,
考察,
即f(1)>f(3)>f(5)>…,∴a>f(1)=﹣4;
若n为偶数,则恒成立,
考察,
即g(2)<g(4)<g(6)<…,
∴;综上所述,;
(Ⅲ)由(1).假设对任意k∈N*,总存在正整数p、q,使ck=cpcq,
则
令q=k+1,则p=k(k+2017)(或q=2k,则p=2k+2016;…)
∴ck=ck(k+2017)ck+1(或ck=c2k+2016c2k;…).
第1页(共3页)
