2020-2021学年九年级数学人教版上册第二十三章旋转 解答题专题过关 试卷(word版无答案)
文档属性
| 名称 | 2020-2021学年九年级数学人教版上册第二十三章旋转 解答题专题过关 试卷(word版无答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-05 00:00:00 | ||
图片预览


文档简介
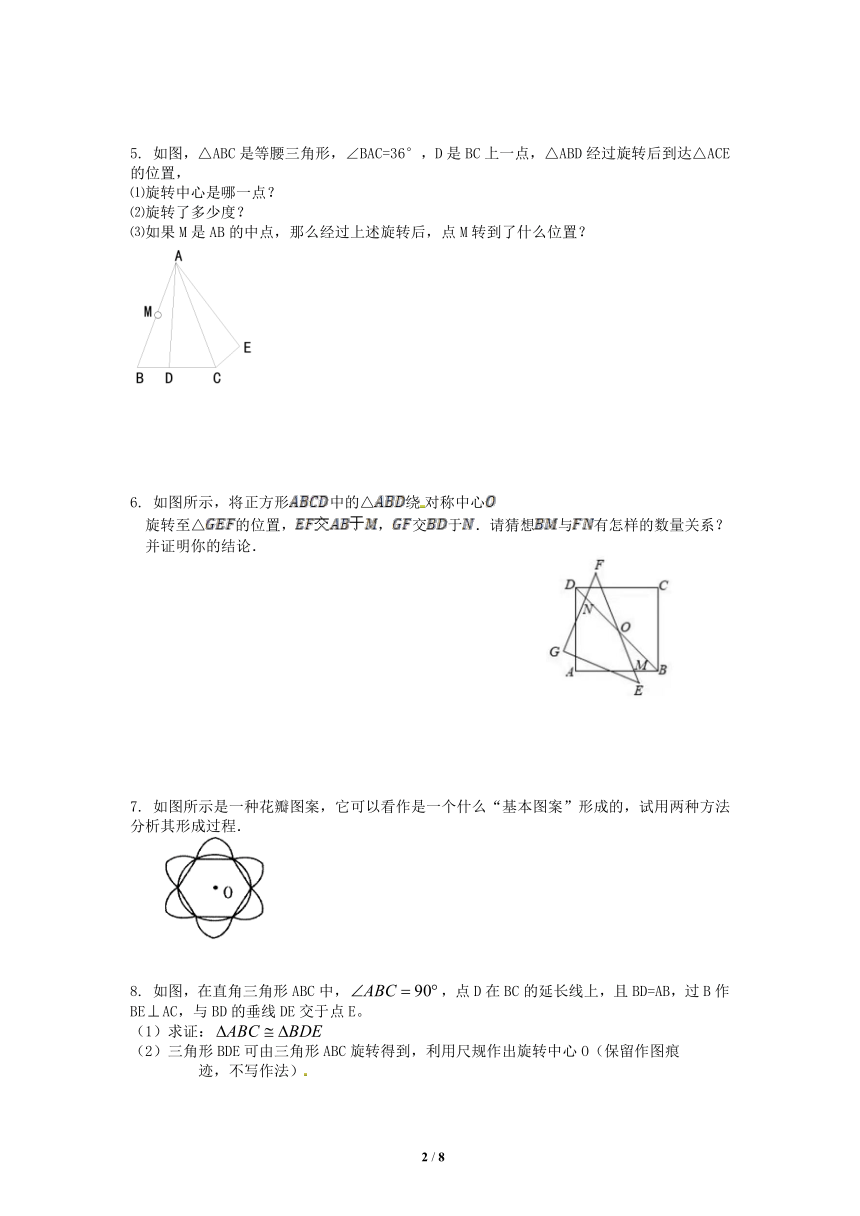
2020-2021学年九年级数学人教版(上)旋转 解答题专题过关
解答题
1. 按要求设计一个图形:所画图形中同时要有正方形和圆,并且这个图形既是轴对称图形又是中心对称图形.
2. 请你设计一幅平面图案满足以下几个要求:①由线段或圆组成;②是轴对称图形;③是中心对称图形.
3. 如图,在中,,,将绕点沿逆时
针方向旋转得到.
(1)线段的长是 ,
的度数是 ;
(2)连结,求证:四边形是平行四边形;
(3)求四边形的面积.
4. 图①②均为的正方形网格,点 在格点上.
(1)在图①中确定格点,并画出以 为顶点的四边形,使其为轴对称图形.(画出一个即可)
(2)在图②中确定格点,并画出以为顶点的四边形,使其为中心对称图形.(画出一个即可)
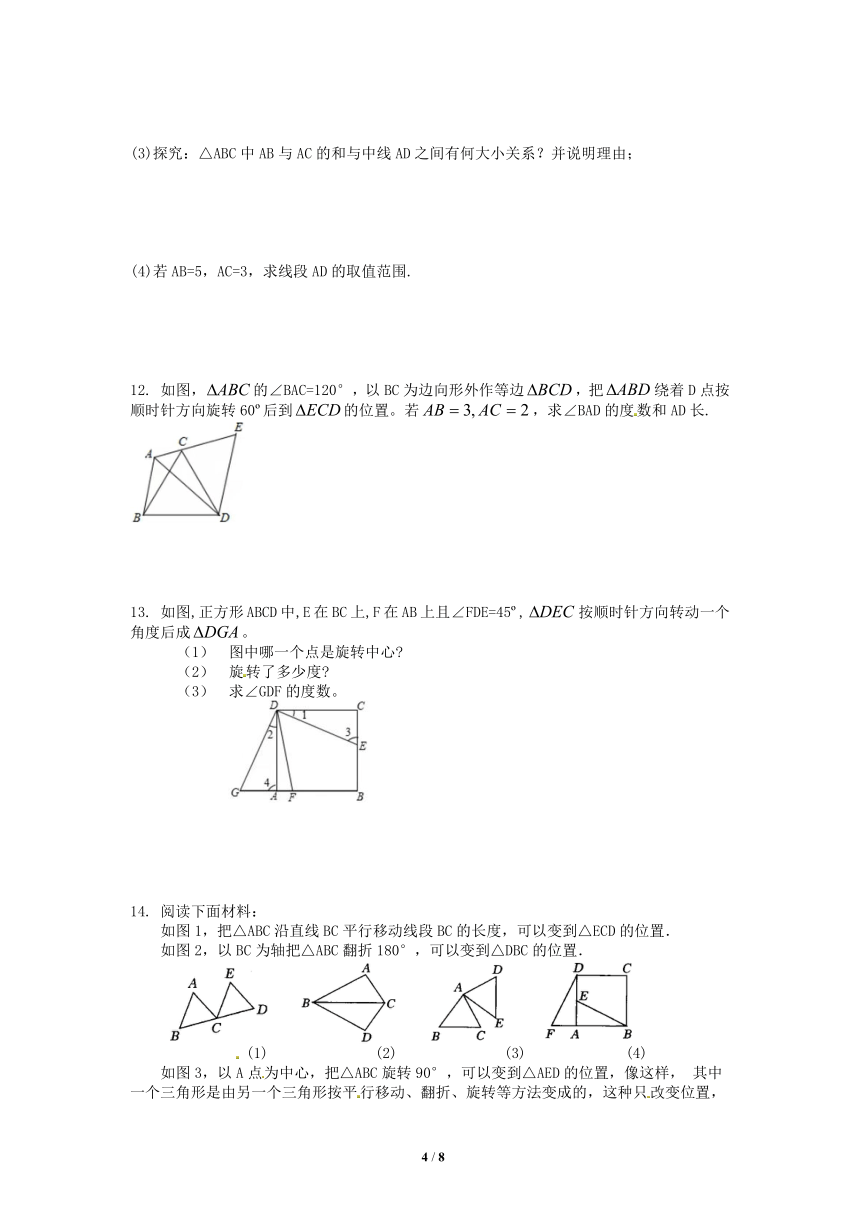
5. 如图,△ABC是等腰三角形,∠BAC=36°,D是BC上一点,△ABD经过旋转后到达△ACE的位置,
⑴旋转中心是哪一点?
⑵旋转了多少度?
⑶如果M是AB的中点,那么经过上述旋转后,点M转到了什么位置?
6. 如图所示,将正方形中的△绕对称中心
旋转至△的位置,,交于.请猜想与有怎样的数量关系?并证明你的结论.
7. 如图所示是一种花瓣图案,它可以看作是一个什么“基本图案”形成的,试用两种方法分析其形成过程.
如图,在直角三角形ABC中,,点D在BC的延长线上,且BD=AB,过B作BEAC,与BD的垂线DE交于点E。
(1)求证:
(2)三角形BDE可由三角形ABC旋转得到,利用尺规作出旋转中心O(保留作图痕
迹,不写作法)
9. 在△ABC中,∠B=10°,∠ACB=20°,AB=4cm,△ABC逆时针旋转一定角度后与△ADE重合,且点C恰好成为AD中点,如图,
⑴指出旋转中心,并求出旋转的度数。
⑵求出∠BAE的度数和AE的长。
10. 如图,在ΔABC中,AB=AC,若将ΔABC绕点C顺时针180 得到ΔFEC。
(1)试猜想AE与BF有何关系,并说明理由;
(2)若ΔABC的面积为3cm2,求四边形ABFE的面积;
(3)当∠ACB为多少度时,四边形ABFE为矩形?说明理由。
11. 如图,在△ABC中,AD是BC边上的中线.
(1)画出与△ACD关于点D成中心对称的三角形;
(2)找出与AC相等的线段;
(3)探究:△ABC中AB与AC的和与中线AD之间有何大小关系?并说明理由;
(4)若AB=5,AC=3,求线段AD的取值范围.
12. 如图,的∠BAC=120°,以BC为边向形外作等边,把绕着D点按顺时针方向旋转60 后到的位置。若,求∠BAD的度数和AD长.
13. 如图,正方形ABCD中,E在BC上,F在AB上且∠FDE=45 ,按顺时针方向转动一个角度后成。
图中哪一个点是旋转中心
旋转了多少度
求∠GDF的度数。
14. 阅读下面材料:
如图1,把△ABC沿直线BC平行移动线段BC的长度,可以变到△ECD的位置.
如图2,以BC为轴把△ABC翻折180°,可以变到△DBC的位置.
(1) (2) (3) (4)
如图3,以A点为中心,把△ABC旋转90°,可以变到△AED的位置,像这样,其中一个三角形是由另一个三角形按平行移动、翻折、旋转等方法变成的,这种只改变位置,不改变形状和大小的图形变换,叫做三角形的全等变换.
回答下列问题
如图4,在正方形ABCD中,E是AD的中点,F是BA延长线上一点,AF=AB.
(1)在如图4所示,可以通过平行移动、翻折、旋转中的哪一种方法,使△ABE移到△ADF的位置?
(2)指出如图4所示中的线段BE与DF之间的关系.
15. 如图,石头A和石头B相距80cm,且关于竹竿L对称,一只电动青蛙在距竹竿30cm,距石头A60cm的P1处,按图中顺序循环跳跃:
(1)请你画出青蛙跳跃的路径(画图工具不作限制).
(2)青蛙跳跃25次后停下,此时它与石头A相距________cm,与竹竿L相距_____cm.
16. 已知正方形ABCD和正方形AEFG有一个公共点A,点G、E分别在线段AD、AB上.
(1) 如图1, 连接DF、BF,若将正方形AEFG绕点A按顺时针方向旋转,判断命题:“在旋转的过程中线段DF与BF的长始终相等.”是否正确,若正确请说明理由,若不正确请举反例说明;
图1
(2) 若将正方形AEFG绕点A按顺时针方向旋转, 连接DG,在旋转的过程中,你能否找到一条线段的长与线段DG的长始终相等.并以图2为例说明理由.
图2
17. 已知,如图□ABCD中,AB⊥AC,AB=1,BC=,对角线AC、BD交于0点,将直线AC绕点0顺时针旋转,分别交BC、AD于点E、F
(1)证明:当旋转角为90°时,四边形ABEF是平行四边形;
(2)试说明在旋转过程中,线段AF与EC总保持相等;
(3)在旋转过程中,四边形BEDF可能是菱形吗 如果不能,请说明理由;如果能,说明理由并求出此时AC绕点0顺时针旋转的度数.
18. 把两个全等的等腰直角三角板ABC和EFG(其直角边长均为4)叠放在一起,如图(1),且三角板EFG的直角顶点G与三角板ABC的斜边的中点O重合,现将三角板EFG绕点O顺时针方向旋转(旋转角α满足的条件:0°<α<90°),四边形CHGK是旋转过程中两个三角板的重叠部分,如图(2).
在上述旋转过程中,BH与CK有怎样的数量关系?四边形CHGK的面积有何变化?证明你发现的结论。
19. 如图1,在正方形ABCD 中,E 是AD 的中点,F 是BA 延长线上的一点,AF=AB
(1)求证△ABE ≌△ADF ;
(2)阅读下列材料:
如图2,把△ABC 沿直线BC平行移动线段BC的长度,可以变到△ECD的位置;
如图3,以BC为轴把△ABC 翻折180o,可以变到△DBC的位置;
如图4,以A为中心把△ABC旋转180o,可以变到△AED的位置.
图2 图3 图4[
像这样,其中一个三角形是由另一个三角形按平行移动、翻折、旋转等方法变成的,这种只改变位置,不改变形状大小的图形变换,叫做三角形的全等变换.
(3)回答下列问题:
①在图1中,可以通过平行移动、翻折、旋转中的哪一种方法使△ 变到△ 的位置,
答:________________________________________________.
②指出图1中,线段BE 与DF 之间的关系
答:________________________________________________.
20. 我们知道:由于圆是中心对称图形,所以过圆心的任何一条直线都可以将圆分割成面积相等的两部分(如图)
探索下列问题:
(1)在图中给出的四个正方形中,各画出一条直线(依次是:水平方向的直线、竖直方向的直线、与水平方向成45°角的直线和任意的直线),将每个正方形都分割成面积相等的两部分;
(2)一条竖直方向的直线m以及任意的直线n,在由左向右平移的过程中,将正六边形分成左右两部分,其面积分别记为S1和S2.
①请你在图中相应图形下方的横线上分别填写S1与S2的数量关系式(用“<”,“=”,“>”连接);
②请你在图23-2-19中分别画出反映S1与S2三种大小关系的直线n,并在相应图形下方的横线上分别填写S1与S2的数量关系式(用“<”,“=”,“>”连接).
(3)是否存在一条直线,将一个任意的平面图形(如图23-2-20所示)分割成面积相等的两部分?请简略说出理由.
21. 一位同学拿了两块45 三角尺△MNK,△ACB做了一个探究活动:将△MNK的直角顶点M放在△ABC的斜边AB的中点处,设AC=BC=a.
如图(1),两三角尺的重叠部分为,则重叠部分的面积为 ,
周长为 .
(2)将图(1)中的绕顶点逆时针旋转,得到图(2),此时重叠部分面
积为 ,周长为 .
如果将绕旋转到不同于图(1)和图(2)的图形,如图(3),请你猜
想此时重叠部分的面积为多少?并试着加以验证.
1 / 3
解答题
1. 按要求设计一个图形:所画图形中同时要有正方形和圆,并且这个图形既是轴对称图形又是中心对称图形.
2. 请你设计一幅平面图案满足以下几个要求:①由线段或圆组成;②是轴对称图形;③是中心对称图形.
3. 如图,在中,,,将绕点沿逆时
针方向旋转得到.
(1)线段的长是 ,
的度数是 ;
(2)连结,求证:四边形是平行四边形;
(3)求四边形的面积.
4. 图①②均为的正方形网格,点 在格点上.
(1)在图①中确定格点,并画出以 为顶点的四边形,使其为轴对称图形.(画出一个即可)
(2)在图②中确定格点,并画出以为顶点的四边形,使其为中心对称图形.(画出一个即可)
5. 如图,△ABC是等腰三角形,∠BAC=36°,D是BC上一点,△ABD经过旋转后到达△ACE的位置,
⑴旋转中心是哪一点?
⑵旋转了多少度?
⑶如果M是AB的中点,那么经过上述旋转后,点M转到了什么位置?
6. 如图所示,将正方形中的△绕对称中心
旋转至△的位置,,交于.请猜想与有怎样的数量关系?并证明你的结论.
7. 如图所示是一种花瓣图案,它可以看作是一个什么“基本图案”形成的,试用两种方法分析其形成过程.
如图,在直角三角形ABC中,,点D在BC的延长线上,且BD=AB,过B作BEAC,与BD的垂线DE交于点E。
(1)求证:
(2)三角形BDE可由三角形ABC旋转得到,利用尺规作出旋转中心O(保留作图痕
迹,不写作法)
9. 在△ABC中,∠B=10°,∠ACB=20°,AB=4cm,△ABC逆时针旋转一定角度后与△ADE重合,且点C恰好成为AD中点,如图,
⑴指出旋转中心,并求出旋转的度数。
⑵求出∠BAE的度数和AE的长。
10. 如图,在ΔABC中,AB=AC,若将ΔABC绕点C顺时针180 得到ΔFEC。
(1)试猜想AE与BF有何关系,并说明理由;
(2)若ΔABC的面积为3cm2,求四边形ABFE的面积;
(3)当∠ACB为多少度时,四边形ABFE为矩形?说明理由。
11. 如图,在△ABC中,AD是BC边上的中线.
(1)画出与△ACD关于点D成中心对称的三角形;
(2)找出与AC相等的线段;
(3)探究:△ABC中AB与AC的和与中线AD之间有何大小关系?并说明理由;
(4)若AB=5,AC=3,求线段AD的取值范围.
12. 如图,的∠BAC=120°,以BC为边向形外作等边,把绕着D点按顺时针方向旋转60 后到的位置。若,求∠BAD的度数和AD长.
13. 如图,正方形ABCD中,E在BC上,F在AB上且∠FDE=45 ,按顺时针方向转动一个角度后成。
图中哪一个点是旋转中心
旋转了多少度
求∠GDF的度数。
14. 阅读下面材料:
如图1,把△ABC沿直线BC平行移动线段BC的长度,可以变到△ECD的位置.
如图2,以BC为轴把△ABC翻折180°,可以变到△DBC的位置.
(1) (2) (3) (4)
如图3,以A点为中心,把△ABC旋转90°,可以变到△AED的位置,像这样,其中一个三角形是由另一个三角形按平行移动、翻折、旋转等方法变成的,这种只改变位置,不改变形状和大小的图形变换,叫做三角形的全等变换.
回答下列问题
如图4,在正方形ABCD中,E是AD的中点,F是BA延长线上一点,AF=AB.
(1)在如图4所示,可以通过平行移动、翻折、旋转中的哪一种方法,使△ABE移到△ADF的位置?
(2)指出如图4所示中的线段BE与DF之间的关系.
15. 如图,石头A和石头B相距80cm,且关于竹竿L对称,一只电动青蛙在距竹竿30cm,距石头A60cm的P1处,按图中顺序循环跳跃:
(1)请你画出青蛙跳跃的路径(画图工具不作限制).
(2)青蛙跳跃25次后停下,此时它与石头A相距________cm,与竹竿L相距_____cm.
16. 已知正方形ABCD和正方形AEFG有一个公共点A,点G、E分别在线段AD、AB上.
(1) 如图1, 连接DF、BF,若将正方形AEFG绕点A按顺时针方向旋转,判断命题:“在旋转的过程中线段DF与BF的长始终相等.”是否正确,若正确请说明理由,若不正确请举反例说明;
图1
(2) 若将正方形AEFG绕点A按顺时针方向旋转, 连接DG,在旋转的过程中,你能否找到一条线段的长与线段DG的长始终相等.并以图2为例说明理由.
图2
17. 已知,如图□ABCD中,AB⊥AC,AB=1,BC=,对角线AC、BD交于0点,将直线AC绕点0顺时针旋转,分别交BC、AD于点E、F
(1)证明:当旋转角为90°时,四边形ABEF是平行四边形;
(2)试说明在旋转过程中,线段AF与EC总保持相等;
(3)在旋转过程中,四边形BEDF可能是菱形吗 如果不能,请说明理由;如果能,说明理由并求出此时AC绕点0顺时针旋转的度数.
18. 把两个全等的等腰直角三角板ABC和EFG(其直角边长均为4)叠放在一起,如图(1),且三角板EFG的直角顶点G与三角板ABC的斜边的中点O重合,现将三角板EFG绕点O顺时针方向旋转(旋转角α满足的条件:0°<α<90°),四边形CHGK是旋转过程中两个三角板的重叠部分,如图(2).
在上述旋转过程中,BH与CK有怎样的数量关系?四边形CHGK的面积有何变化?证明你发现的结论。
19. 如图1,在正方形ABCD 中,E 是AD 的中点,F 是BA 延长线上的一点,AF=AB
(1)求证△ABE ≌△ADF ;
(2)阅读下列材料:
如图2,把△ABC 沿直线BC平行移动线段BC的长度,可以变到△ECD的位置;
如图3,以BC为轴把△ABC 翻折180o,可以变到△DBC的位置;
如图4,以A为中心把△ABC旋转180o,可以变到△AED的位置.
图2 图3 图4[
像这样,其中一个三角形是由另一个三角形按平行移动、翻折、旋转等方法变成的,这种只改变位置,不改变形状大小的图形变换,叫做三角形的全等变换.
(3)回答下列问题:
①在图1中,可以通过平行移动、翻折、旋转中的哪一种方法使△ 变到△ 的位置,
答:________________________________________________.
②指出图1中,线段BE 与DF 之间的关系
答:________________________________________________.
20. 我们知道:由于圆是中心对称图形,所以过圆心的任何一条直线都可以将圆分割成面积相等的两部分(如图)
探索下列问题:
(1)在图中给出的四个正方形中,各画出一条直线(依次是:水平方向的直线、竖直方向的直线、与水平方向成45°角的直线和任意的直线),将每个正方形都分割成面积相等的两部分;
(2)一条竖直方向的直线m以及任意的直线n,在由左向右平移的过程中,将正六边形分成左右两部分,其面积分别记为S1和S2.
①请你在图中相应图形下方的横线上分别填写S1与S2的数量关系式(用“<”,“=”,“>”连接);
②请你在图23-2-19中分别画出反映S1与S2三种大小关系的直线n,并在相应图形下方的横线上分别填写S1与S2的数量关系式(用“<”,“=”,“>”连接).
(3)是否存在一条直线,将一个任意的平面图形(如图23-2-20所示)分割成面积相等的两部分?请简略说出理由.
21. 一位同学拿了两块45 三角尺△MNK,△ACB做了一个探究活动:将△MNK的直角顶点M放在△ABC的斜边AB的中点处,设AC=BC=a.
如图(1),两三角尺的重叠部分为,则重叠部分的面积为 ,
周长为 .
(2)将图(1)中的绕顶点逆时针旋转,得到图(2),此时重叠部分面
积为 ,周长为 .
如果将绕旋转到不同于图(1)和图(2)的图形,如图(3),请你猜
想此时重叠部分的面积为多少?并试着加以验证.
1 / 3
同课章节目录
