1.7.1《定积分在几何中的应用》人教版高中数学选修2-2 课件(共28张PPT)
文档属性
| 名称 | 1.7.1《定积分在几何中的应用》人教版高中数学选修2-2 课件(共28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-06 22:03:30 | ||
图片预览





文档简介
(共28张PPT)
讲解人:X X X 时间:20XX.XX.XX
PEOPLE'S EDUCATION PRESS HIGH SCHOOL MATHEMATICS ELECTIVE 2-2
1.7.1定积分在几何中的应用
第1章 导数及其应用
人教版高中数学选修2-2
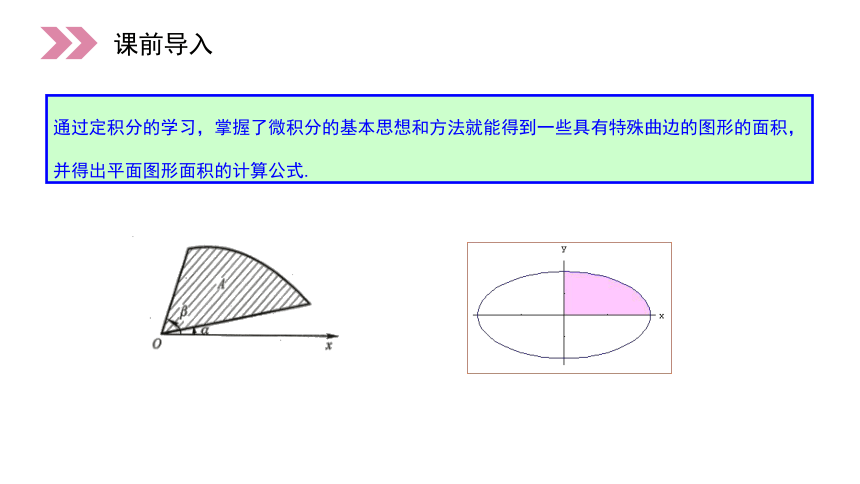
这些平面图形面积问题在几何中用初等数学方法能解决吗?
a
0
x
y
b
课前导入
通过定积分的学习,掌握了微积分的基本思想和方法就能得到一些具有特殊曲边的图形的面积,并得出平面图形面积的计算公式.
课前导入
第三步:写出整体量 的近似值,
第四步:取 时的 则得
第一步:将所求量 分为部分量之和,即: ;
第二步:求出每个部分量的近似值,
用定积分概念解决实际问题的四个步骤:
课前导入
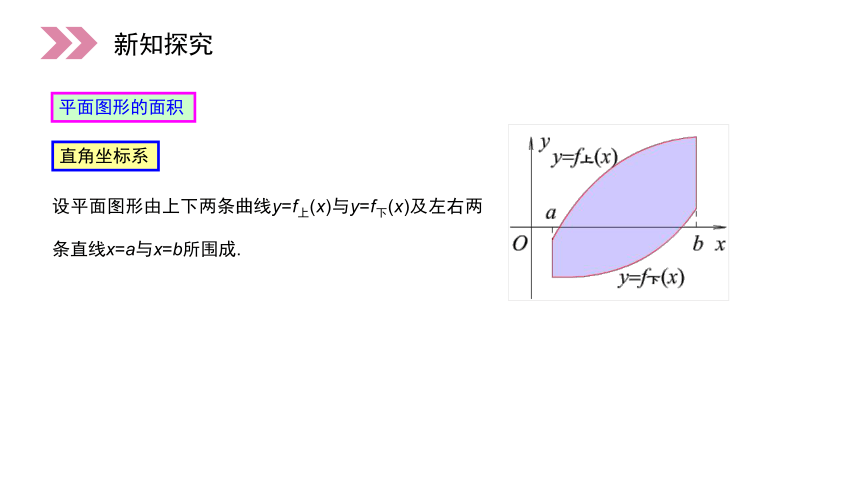
设平面图形由上下两条曲线y=f上(x)与y=f下(x)及左右两条直线x=a与x=b所围成.
直角坐标系
平面图形的面积
新知探究
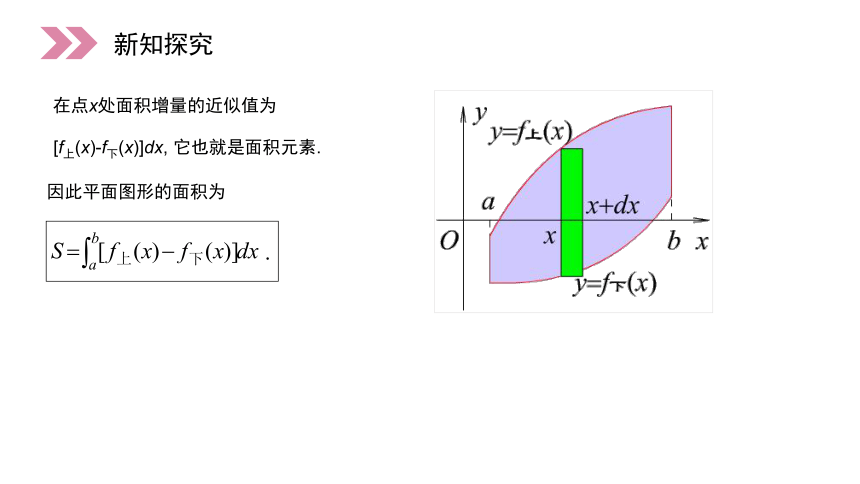
[f上(x)-f下(x)]dx, 它也就是面积元素.
因此平面图形的面积为
在点x处面积增量的近似值为
新知探究
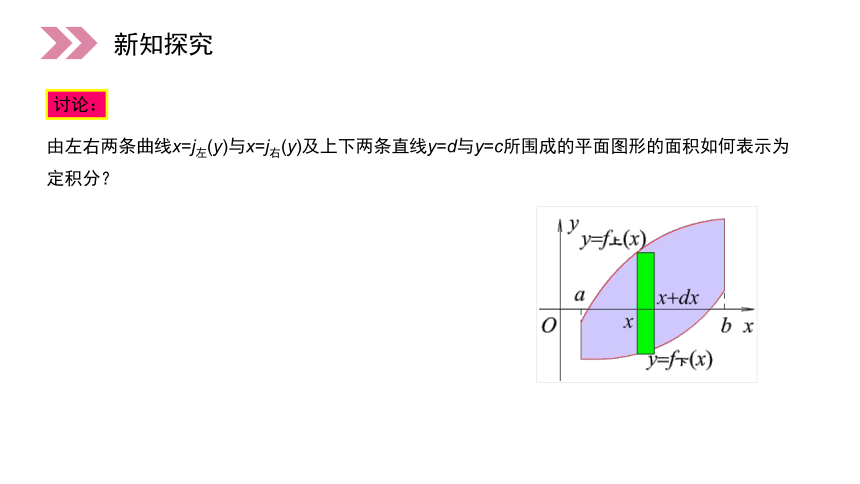
由左右两条曲线x=j左(y)与x=j右(y)及上下两条直线y=d与y=c所围成的平面图形的面积如何表示为定积分?
讨论:
新知探究
面积为
面积元素为[j右(y)-j左(y)]dy,
提示:
新知探究
首先根据题意画出曲线 的草图,在图中找出所求面积的区域,图形结合,直观解题;其次,为了确定出被积函数和积分的上、下限,我们需要求出两条曲线的交点的横坐标.
计算两条抛物线 在第一象限所围图形的面积 .
例1
新知探究
从图中可以看出,所求图形的面积可以为两个曲边梯形面积的差,进而可用定积分求面积S.
新知探究
解: 方程组:
得交点的横坐标
因此,所求图形的面积为
新知探究
计算抛物线y2= 、直线y=x-4和x轴所围成的图形的面积S.
首先画出草图,并设法把所求图形的面积问题转化为求曲边梯形的面积问题.其次,确定被积函数和积分的上、下限.
例2
新知探究
由图可知,我们需要把所求图形的面积分成两部分 .需要求出直线y=x-4 与曲线 的交点的横坐标,直线 y=x-4 与x轴的交点.
新知探究
得直线y=x-4与曲线y= 交点的坐标为(8,4).直线y=x-4与x轴的交点为(4,0).
解:所求面积为图中阴影部分的面积.
解方程组
新知探究
因此,所求图形面积为
新知探究
计算由曲线 和 所围成的图形的面积.
首先画出草图,并设法把所求图形的面积问题转化为求两部分的面积问题.其次,确定被积函数和积分的上、下限.
例3
新知探究
由图可知,我们需要把所求图形的面积分成两部分 .需要求出曲线 、曲线 两个交点.
新知探究
得两曲线的交点的坐标为(0,0),(-2,4),(3,9).
解:所求面积为图中阴影部分的面积.
解方程组
选x为积分变量x∈[-2,3]
于是所求面积
新知探究
平面图形的面积求法小结:
(1)画图
(2)确定图形范围,通过解方程组确定上下限
(3)确定被积函数(注意上下位置)
(4)写出平面图形面积的积分表达式
(5)利用微积分基本定理求出面积
新知探究
求由 相交围成的平面图形的面积
若函数 相交, 则两条曲线所围形的面积为
显然在具体的题目中,需要首先把函数的图形画出来,然后才写出具体的面积表达式.
新知探究
曲边扇形面积元素
曲边扇形的面积公式
极坐标方程的情形
设由曲线 及射线 围成一曲边扇形,求其面积.这里 在 上连续,且 .
新知探究
因为曲线关于x轴对称,所以只须考虑第一象限中的情况.
求曲线 围成的图形的面积.
例4
新知探究
取 为积分变量,则 设区间 ,所对应的曲边扇形的面积为 则面积元素 就是用区间 所对应的扇形面积代替曲边扇形的面积 .
新知探究
解:(1) 确定积分变量和积分区间:取 为积分变量,
(2) 求微元:任取 则面积元素 就是区间 所对应的扇形面积,
(3) 求定积分: 第一象限图形的面积表示为
则所求的几何面积为
新知探究
设函数 ,若 ,则 的值为__________.
1、
课堂练习
求由 所围成图形的面积.
2、
课堂练习
解:(1) 确定积分变量和积分区间:由于曲线 和 的交点为 和 .
取x为积分变量, 则
所求的几何图形的面积表示为
直角坐标方程给出的平面图形的面积一般以直角坐标为积分变量;
极坐标方程给出的平面图形的面积一般以由极坐标为积分变量;
曲边梯形的面积的计算一般以由直角坐标为积分变量;曲边扇形的面积的计算一般以由极坐标为积分变量.
课堂小结
讲解人:X X X 时间:20XX.XX.XX
PEOPLE'S EDUCATION PRESS HIGH SCHOOL MATHEMATICS ELECTIVE 2-2
感谢你的聆听
第1章 导数及其应用
人教版高中数学选修2-2
讲解人:X X X 时间:20XX.XX.XX
PEOPLE'S EDUCATION PRESS HIGH SCHOOL MATHEMATICS ELECTIVE 2-2
1.7.1定积分在几何中的应用
第1章 导数及其应用
人教版高中数学选修2-2
这些平面图形面积问题在几何中用初等数学方法能解决吗?
a
0
x
y
b
课前导入
通过定积分的学习,掌握了微积分的基本思想和方法就能得到一些具有特殊曲边的图形的面积,并得出平面图形面积的计算公式.
课前导入
第三步:写出整体量 的近似值,
第四步:取 时的 则得
第一步:将所求量 分为部分量之和,即: ;
第二步:求出每个部分量的近似值,
用定积分概念解决实际问题的四个步骤:
课前导入
设平面图形由上下两条曲线y=f上(x)与y=f下(x)及左右两条直线x=a与x=b所围成.
直角坐标系
平面图形的面积
新知探究
[f上(x)-f下(x)]dx, 它也就是面积元素.
因此平面图形的面积为
在点x处面积增量的近似值为
新知探究
由左右两条曲线x=j左(y)与x=j右(y)及上下两条直线y=d与y=c所围成的平面图形的面积如何表示为定积分?
讨论:
新知探究
面积为
面积元素为[j右(y)-j左(y)]dy,
提示:
新知探究
首先根据题意画出曲线 的草图,在图中找出所求面积的区域,图形结合,直观解题;其次,为了确定出被积函数和积分的上、下限,我们需要求出两条曲线的交点的横坐标.
计算两条抛物线 在第一象限所围图形的面积 .
例1
新知探究
从图中可以看出,所求图形的面积可以为两个曲边梯形面积的差,进而可用定积分求面积S.
新知探究
解: 方程组:
得交点的横坐标
因此,所求图形的面积为
新知探究
计算抛物线y2= 、直线y=x-4和x轴所围成的图形的面积S.
首先画出草图,并设法把所求图形的面积问题转化为求曲边梯形的面积问题.其次,确定被积函数和积分的上、下限.
例2
新知探究
由图可知,我们需要把所求图形的面积分成两部分 .需要求出直线y=x-4 与曲线 的交点的横坐标,直线 y=x-4 与x轴的交点.
新知探究
得直线y=x-4与曲线y= 交点的坐标为(8,4).直线y=x-4与x轴的交点为(4,0).
解:所求面积为图中阴影部分的面积.
解方程组
新知探究
因此,所求图形面积为
新知探究
计算由曲线 和 所围成的图形的面积.
首先画出草图,并设法把所求图形的面积问题转化为求两部分的面积问题.其次,确定被积函数和积分的上、下限.
例3
新知探究
由图可知,我们需要把所求图形的面积分成两部分 .需要求出曲线 、曲线 两个交点.
新知探究
得两曲线的交点的坐标为(0,0),(-2,4),(3,9).
解:所求面积为图中阴影部分的面积.
解方程组
选x为积分变量x∈[-2,3]
于是所求面积
新知探究
平面图形的面积求法小结:
(1)画图
(2)确定图形范围,通过解方程组确定上下限
(3)确定被积函数(注意上下位置)
(4)写出平面图形面积的积分表达式
(5)利用微积分基本定理求出面积
新知探究
求由 相交围成的平面图形的面积
若函数 相交, 则两条曲线所围形的面积为
显然在具体的题目中,需要首先把函数的图形画出来,然后才写出具体的面积表达式.
新知探究
曲边扇形面积元素
曲边扇形的面积公式
极坐标方程的情形
设由曲线 及射线 围成一曲边扇形,求其面积.这里 在 上连续,且 .
新知探究
因为曲线关于x轴对称,所以只须考虑第一象限中的情况.
求曲线 围成的图形的面积.
例4
新知探究
取 为积分变量,则 设区间 ,所对应的曲边扇形的面积为 则面积元素 就是用区间 所对应的扇形面积代替曲边扇形的面积 .
新知探究
解:(1) 确定积分变量和积分区间:取 为积分变量,
(2) 求微元:任取 则面积元素 就是区间 所对应的扇形面积,
(3) 求定积分: 第一象限图形的面积表示为
则所求的几何面积为
新知探究
设函数 ,若 ,则 的值为__________.
1、
课堂练习
求由 所围成图形的面积.
2、
课堂练习
解:(1) 确定积分变量和积分区间:由于曲线 和 的交点为 和 .
取x为积分变量, 则
所求的几何图形的面积表示为
直角坐标方程给出的平面图形的面积一般以直角坐标为积分变量;
极坐标方程给出的平面图形的面积一般以由极坐标为积分变量;
曲边梯形的面积的计算一般以由直角坐标为积分变量;曲边扇形的面积的计算一般以由极坐标为积分变量.
课堂小结
讲解人:X X X 时间:20XX.XX.XX
PEOPLE'S EDUCATION PRESS HIGH SCHOOL MATHEMATICS ELECTIVE 2-2
感谢你的聆听
第1章 导数及其应用
人教版高中数学选修2-2
