1.1.1《变化率问题》人教版高中数学选修2-2 课件(共29张PPT)
文档属性
| 名称 | 1.1.1《变化率问题》人教版高中数学选修2-2 课件(共29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 957.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-06 22:04:07 | ||
图片预览







文档简介
(共29张PPT)
讲解人:X X X 时间:20XX.XX.XX
PEOPLE'S EDUCATION PRESS HIGH SCHOOL MATHEMATICS ELECTIVE 2-2
1.1.1 变化率问题
第1章 导数及其应用
人教版高中数学选修2-2
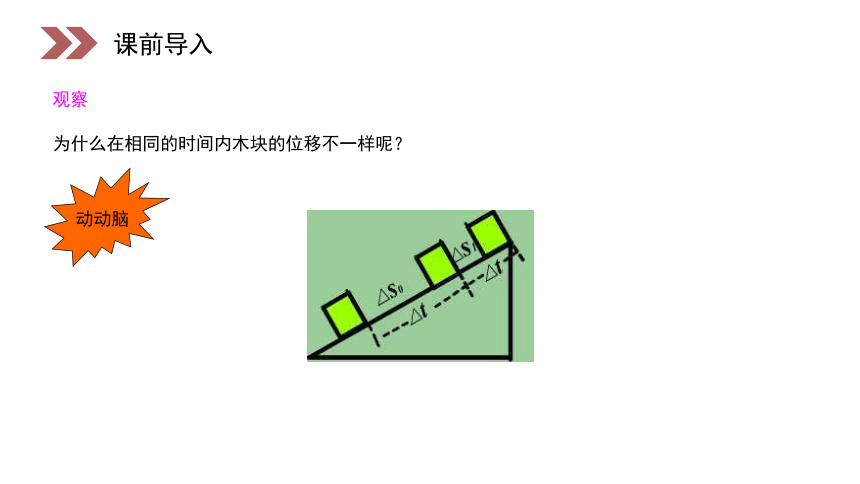
为什么在相同的时间内木块的位移不一样呢?
动动脑
观察
课前导入
观察
为什么跳水运动员的速度越来越快呢?
课前导入
课前导入
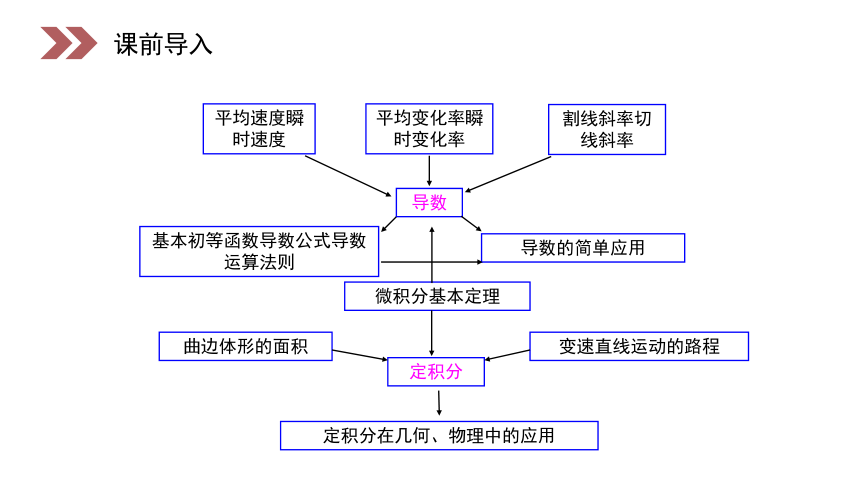
解决以上2个问题,就需要我们来学习一种新的函数来解释这种现象!
平均速度瞬时速度
平均变化率瞬时变化率
割线斜率切线斜率
导数
基本初等函数导数公式导数运算法则
导数的简单应用
微积分基本定理
定积分
曲边体形的面积
变速直线运动的路程
定积分在几何、物理中的应用
课前导入
问题1 气球膨胀率
新知探究
我们都吹过气球回忆一下吹气球的过程,可以发现,随着气球内空气容量的增加,气球的半径增加越来越慢.从数学角度,如何描述这种现象呢
我们来分析一下:
气球的体积V(单位:L)与半径r单位:(dm)
之间的函数关系是
如果将半径r表示为体积V的函数,那么
新知探究
当V从0增加到1时,气球半径增加气球的平均膨胀率为
当V从1增加到2时,气球半径增加气球的平均膨胀率为
显然0.62>0.16
我们来分析一下:
新知探究
思考
当空气容量从V1增加到V2时,气球的平均膨胀率是多少
你想对了吗?
新知探究
问题2 高台跳水
想想运动员跳水的过程?
新知探究
在高台跳水运动中,运动员相对于水面的高度h(单位:米)与起跳后的时间t(单位:秒)存在函数关系
h(t)=-4.9t2+6.5t+10.
如何用运动员在某些时间段内的平均速度粗略地描述其运动状态
请计算
0≦t≦0.5和1≦t≦2时的平均速度
在0 ≦t ≦0.5这段时间里
在1 ≦t ≦2这段时间里
新知探究
探究
计算运动员在 这段时间里的平均速度,并思考下面的问题:
(1)运动员在这段时间里是静止的吗?
(2)你认为用平均速度描述运动员运动状态有什么问题?
新知探究
平均速度不能反映他在这段时间里运动状态,需要用瞬时速度描述运动状态.
新知探究
同学们,从上面的问题中能够发现什么共同点呢?
总结
新知探究
以上两个问题都是求变化率,我们可以用函数关系式y=f(x)来表示. 那么变化率为
上述问题中的变化率可用式子 表示称为函数f(x)从x1到x2的平均变化率.
很重要!
知识要点
新知探究
一般我们用Δx 表示 , 即 .
新知探究
是一个整体符号,而不是 与 相乘.
注意!
很重要!
新知探究
例题1
1 、已知函数f(x)=-x2的图象上的一点A(-1,-1)及临近一点B(0,0),则Δy/Δx=( )
A. 3 B. 4 C. 1 D. -1
c
新知探究
解:
=0-(-1)=1;
=0-(-1)=1;
观察函数f(x)的图象
平均变化率
表示什么
O
A
B
x
y
Y=f(x)
x1
x2
f(x1)
f(x2)
X2-x1
f(x2)-f(x1)
直线AB的斜率
例题2
新知探究
汽车在前两秒内速度由0增加到10m/s,在后两秒内增至30m/s,其运动状态如何呢?
如果我们用平均速度描述其运动状态,
前两秒内: v=5 (m/s)
后两秒内:v=10 (m/s)
你想对了吗?
例题3
新知探究
想一想
你还能想到生活中类似的问题吗?举个例子吧!
新知探究
我们把式子 称为函数 f(x)从 到 的平均变化 率 . ( average rate of change)
课堂小结
平均变化率的求解步骤:
(1)求函数的增量Δf=Δy=f(x2)-f(x1);
(2)计算平均变化率
1 、已知函数f(x)=-x2+x的图象上的一点A(-1,-2)及临近一点B(-1+Δx,-2+Δy),
则Δy/Δx=( )
A . 3 B. 3Δx-(Δx)2
C. 3-(Δx)2 D. 3-Δx
D
课堂练习
2 、函数 在区间 上的平均变化率是( )
A.4 B.2
C.
D.
B
课堂练习
3、函数 在区间[1,1.5]上的平均变化率为_______________.
5
解:由平均变化率的公式
课堂练习
4、已知函数 ,则变化率可用式子_____________,此式称之为函数从 到 的___________. 平均变化率可以表示为_____________.
平均变化率
你做对了吗?
课堂练习
5、过曲线y=f(x)=x3上两点P(1,1)和Q (1+Δx,1+Δy)作曲线的割线,求出当Δx=0.1时割线的斜率.
解: K=3Δx+(Δx)2=3+3×0.1+(0.1)2=3.31.
课堂练习
6、已知一次函数 在区间[-2,6]上的平均变化率为2,且函数图象过点(0,2),试求此一次函数的表达式.
课堂练习
解:由平均变化率的含义可知该直线的斜率为2,设直线方程为y=2x+b,
又因为直线经过点(0,2),代入方程得b=2.
则直线方程为:y=2x+2.
讲解人:X X X 时间:20XX.XX.XX
PEOPLE'S EDUCATION PRESS HIGH SCHOOL MATHEMATICS ELECTIVE 2-2
感谢你的聆听
第1章 导数及其应用
人教版高中数学选修2-2
讲解人:X X X 时间:20XX.XX.XX
PEOPLE'S EDUCATION PRESS HIGH SCHOOL MATHEMATICS ELECTIVE 2-2
1.1.1 变化率问题
第1章 导数及其应用
人教版高中数学选修2-2
为什么在相同的时间内木块的位移不一样呢?
动动脑
观察
课前导入
观察
为什么跳水运动员的速度越来越快呢?
课前导入
课前导入
解决以上2个问题,就需要我们来学习一种新的函数来解释这种现象!
平均速度瞬时速度
平均变化率瞬时变化率
割线斜率切线斜率
导数
基本初等函数导数公式导数运算法则
导数的简单应用
微积分基本定理
定积分
曲边体形的面积
变速直线运动的路程
定积分在几何、物理中的应用
课前导入
问题1 气球膨胀率
新知探究
我们都吹过气球回忆一下吹气球的过程,可以发现,随着气球内空气容量的增加,气球的半径增加越来越慢.从数学角度,如何描述这种现象呢
我们来分析一下:
气球的体积V(单位:L)与半径r单位:(dm)
之间的函数关系是
如果将半径r表示为体积V的函数,那么
新知探究
当V从0增加到1时,气球半径增加气球的平均膨胀率为
当V从1增加到2时,气球半径增加气球的平均膨胀率为
显然0.62>0.16
我们来分析一下:
新知探究
思考
当空气容量从V1增加到V2时,气球的平均膨胀率是多少
你想对了吗?
新知探究
问题2 高台跳水
想想运动员跳水的过程?
新知探究
在高台跳水运动中,运动员相对于水面的高度h(单位:米)与起跳后的时间t(单位:秒)存在函数关系
h(t)=-4.9t2+6.5t+10.
如何用运动员在某些时间段内的平均速度粗略地描述其运动状态
请计算
0≦t≦0.5和1≦t≦2时的平均速度
在0 ≦t ≦0.5这段时间里
在1 ≦t ≦2这段时间里
新知探究
探究
计算运动员在 这段时间里的平均速度,并思考下面的问题:
(1)运动员在这段时间里是静止的吗?
(2)你认为用平均速度描述运动员运动状态有什么问题?
新知探究
平均速度不能反映他在这段时间里运动状态,需要用瞬时速度描述运动状态.
新知探究
同学们,从上面的问题中能够发现什么共同点呢?
总结
新知探究
以上两个问题都是求变化率,我们可以用函数关系式y=f(x)来表示. 那么变化率为
上述问题中的变化率可用式子 表示称为函数f(x)从x1到x2的平均变化率.
很重要!
知识要点
新知探究
一般我们用Δx 表示 , 即 .
新知探究
是一个整体符号,而不是 与 相乘.
注意!
很重要!
新知探究
例题1
1 、已知函数f(x)=-x2的图象上的一点A(-1,-1)及临近一点B(0,0),则Δy/Δx=( )
A. 3 B. 4 C. 1 D. -1
c
新知探究
解:
=0-(-1)=1;
=0-(-1)=1;
观察函数f(x)的图象
平均变化率
表示什么
O
A
B
x
y
Y=f(x)
x1
x2
f(x1)
f(x2)
X2-x1
f(x2)-f(x1)
直线AB的斜率
例题2
新知探究
汽车在前两秒内速度由0增加到10m/s,在后两秒内增至30m/s,其运动状态如何呢?
如果我们用平均速度描述其运动状态,
前两秒内: v=5 (m/s)
后两秒内:v=10 (m/s)
你想对了吗?
例题3
新知探究
想一想
你还能想到生活中类似的问题吗?举个例子吧!
新知探究
我们把式子 称为函数 f(x)从 到 的平均变化 率 . ( average rate of change)
课堂小结
平均变化率的求解步骤:
(1)求函数的增量Δf=Δy=f(x2)-f(x1);
(2)计算平均变化率
1 、已知函数f(x)=-x2+x的图象上的一点A(-1,-2)及临近一点B(-1+Δx,-2+Δy),
则Δy/Δx=( )
A . 3 B. 3Δx-(Δx)2
C. 3-(Δx)2 D. 3-Δx
D
课堂练习
2 、函数 在区间 上的平均变化率是( )
A.4 B.2
C.
D.
B
课堂练习
3、函数 在区间[1,1.5]上的平均变化率为_______________.
5
解:由平均变化率的公式
课堂练习
4、已知函数 ,则变化率可用式子_____________,此式称之为函数从 到 的___________. 平均变化率可以表示为_____________.
平均变化率
你做对了吗?
课堂练习
5、过曲线y=f(x)=x3上两点P(1,1)和Q (1+Δx,1+Δy)作曲线的割线,求出当Δx=0.1时割线的斜率.
解: K=3Δx+(Δx)2=3+3×0.1+(0.1)2=3.31.
课堂练习
6、已知一次函数 在区间[-2,6]上的平均变化率为2,且函数图象过点(0,2),试求此一次函数的表达式.
课堂练习
解:由平均变化率的含义可知该直线的斜率为2,设直线方程为y=2x+b,
又因为直线经过点(0,2),代入方程得b=2.
则直线方程为:y=2x+2.
讲解人:X X X 时间:20XX.XX.XX
PEOPLE'S EDUCATION PRESS HIGH SCHOOL MATHEMATICS ELECTIVE 2-2
感谢你的聆听
第1章 导数及其应用
人教版高中数学选修2-2
