1.7.2《定积分在物理中的应用》人教版高中数学选修2-2 课件(共19张PPT)
文档属性
| 名称 | 1.7.2《定积分在物理中的应用》人教版高中数学选修2-2 课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-06 22:07:34 | ||
图片预览






文档简介
(共19张PPT)
讲解人:X X X 时间:20XX.XX.XX
PEOPLE'S EDUCATION PRESS HIGH SCHOOL MATHEMATICS ELECTIVE 2-2
1.7.2定积分在物理中的应用
第1章 导数及其应用
人教版高中数学选修2-2
定积分的物理应用包括作功、水压力和引力等问题。本节仅给出作功、水压力和引力问题的例子.
课前导入
定积分的物理应用包括变速直线运动作功、水压力和引力等.本节仅给出变速直线运动作功、水压力和引力问题的例子.
变速直线运动的路程
做变速直线运动的物体所经过的路程s,等于其速度函数 在时间区间[a,b]上的定积分,即
新知探究
例1
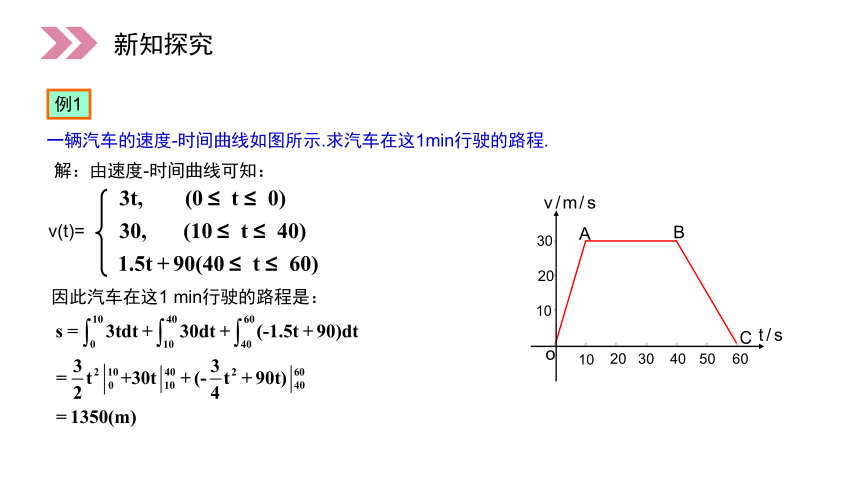
一辆汽车的速度-时间曲线如图所示.求汽车在这1min行驶的路程.
新知探究
解:由速度-时间曲线可知:
v(t)=
因此汽车在这1 min行驶的路程是:
变力做功
由物理学知道,如果一个物体在恒力F作用下,使得物体沿力的方向作直线运动 ,物体有位移 s 时,力F对物体所作的功为:W=F*s
新知探究
探究
如果物体在变力F(x)的作用下做直线运动,并且物体沿着与F(x)相同方向从x=a移动到x=b(a新知探究
与求曲边梯形的面积和求变速直线运动的路程一样,可以用“四步曲”解决变力作功问题可以得到
分割、近似代替、求和、取极限
如图,在弹性限度内,将一弹簧从平衡位置拉倒离平衡位置l m处,求克服弹力所作的功.
例2
新知探究
解:在弹性限度内,拉伸(或压缩)弹簧所需的力F(x)与弹簧拉伸(或压缩)的长度成正比,即F(x)=kx,其中常数k是比例系数.
由变力做功公式,得到
答:克服弹力所作的功为 .
两个质量分别为 ,相距为 r 的质点间的引力
万有引力定律
若要计算一细长杆对一质点的引力,此时由于细杆上各点与质点的距离是变化的,所以不能直接利用上述公式计算.
新知探究
例3
设有一长为 l 质量为 M 的均匀细杆,另有一质量为 m 的质点和杆在一条直线上,它到杆的近端距离为 a ,求细杆对质点的引力.
新知探究
取坐标系如图,取 x 为积分变量
0
l
·
m
a
该小段细杆的质量为
若把问题改为求细杆对位于它的一端垂线上距杆 a 处的质量为 m 质点的引力.
新知探究
解:如图建立坐标系
新知探究
将半径为 的半球形水池内注满水,若将满池水全部抽出,需作多少功?
例4
新知探究
分析:吸水作功是水的重力在作功问题,此问题可理解成将水一层一层吸出的.取坐标原点在水平面, 轴铅直向下 ,如果
设 所对应的薄层的体积为圆柱体体积, 那么在 上以直代曲,便得体积元素从而得到重力作功的功元素 .
(2) 分割 : 对 把区间 所对应的薄层的体积用圆柱体体积代替,得到
解: (1) 确定积分变量和积分区间:
建立如图所示的坐标系.
则半圆的方程为 取x为积分变量, 则
新知探究
由于将这一薄层水吸出是这一薄层水的重力在作功,设水的比重为 所以功的元素为
(3) 求定积分:将满池水全部抽出所作的功为
新知探究
1、
用铁锤把钉子钉入木板,设木板对铁钉的阻力与铁钉进入木板的深度成正比,铁锤在第一次锤击时将铁钉击入1厘米,若每次锤击所作的功相等,问第 次锤击时又将铁钉击入多少?
课堂练习
解:
设木板对铁钉的阻力为
第一次锤击时所作的功为
设 次击入的总深度为 厘米
次锤击所作的总功为
依题意知,每次锤击所作的功相等.
次击入的总深度为
第 次击入的深度为
2、
将直角边各为a及2a的直角三角形薄片垂直地浸入水中,斜边朝下,直角边的边长与水面平行,且该边到水面的距离恰等于该边的边长,求薄板所受的侧压力?
课堂练习
解:建立坐标系如图
面积微元
思考题
一球完全浸没水中,问该球面所受的总压力与球浸没的深度有无关系?它所受的总压力与它在水中受到的浮力有何关系?
3、
课堂练习
该球面所受的总压力方向向上(下半球面所受的压力大于上半球面),其值为该球排开水的重量,即球的体积,也就是它在水中受到的浮力.因此该球面所受的总压力与球浸没的深度无关.
一圆柱形蓄水池高为5米,底半径为3米,底半径为3米,池内盛满了水全部吸出,需作多少功?
4、
解:建立坐标系如图
这一薄层水的重力为
功元素为
(千焦).
讲解人:X X X 时间:20XX.XX.XX
PEOPLE'S EDUCATION PRESS HIGH SCHOOL MATHEMATICS ELECTIVE 2-2
感谢你的聆听
第1章 导数及其应用
人教版高中数学选修2-2
讲解人:X X X 时间:20XX.XX.XX
PEOPLE'S EDUCATION PRESS HIGH SCHOOL MATHEMATICS ELECTIVE 2-2
1.7.2定积分在物理中的应用
第1章 导数及其应用
人教版高中数学选修2-2
定积分的物理应用包括作功、水压力和引力等问题。本节仅给出作功、水压力和引力问题的例子.
课前导入
定积分的物理应用包括变速直线运动作功、水压力和引力等.本节仅给出变速直线运动作功、水压力和引力问题的例子.
变速直线运动的路程
做变速直线运动的物体所经过的路程s,等于其速度函数 在时间区间[a,b]上的定积分,即
新知探究
例1
一辆汽车的速度-时间曲线如图所示.求汽车在这1min行驶的路程.
新知探究
解:由速度-时间曲线可知:
v(t)=
因此汽车在这1 min行驶的路程是:
变力做功
由物理学知道,如果一个物体在恒力F作用下,使得物体沿力的方向作直线运动 ,物体有位移 s 时,力F对物体所作的功为:W=F*s
新知探究
探究
如果物体在变力F(x)的作用下做直线运动,并且物体沿着与F(x)相同方向从x=a移动到x=b(a
与求曲边梯形的面积和求变速直线运动的路程一样,可以用“四步曲”解决变力作功问题可以得到
分割、近似代替、求和、取极限
如图,在弹性限度内,将一弹簧从平衡位置拉倒离平衡位置l m处,求克服弹力所作的功.
例2
新知探究
解:在弹性限度内,拉伸(或压缩)弹簧所需的力F(x)与弹簧拉伸(或压缩)的长度成正比,即F(x)=kx,其中常数k是比例系数.
由变力做功公式,得到
答:克服弹力所作的功为 .
两个质量分别为 ,相距为 r 的质点间的引力
万有引力定律
若要计算一细长杆对一质点的引力,此时由于细杆上各点与质点的距离是变化的,所以不能直接利用上述公式计算.
新知探究
例3
设有一长为 l 质量为 M 的均匀细杆,另有一质量为 m 的质点和杆在一条直线上,它到杆的近端距离为 a ,求细杆对质点的引力.
新知探究
取坐标系如图,取 x 为积分变量
0
l
·
m
a
该小段细杆的质量为
若把问题改为求细杆对位于它的一端垂线上距杆 a 处的质量为 m 质点的引力.
新知探究
解:如图建立坐标系
新知探究
将半径为 的半球形水池内注满水,若将满池水全部抽出,需作多少功?
例4
新知探究
分析:吸水作功是水的重力在作功问题,此问题可理解成将水一层一层吸出的.取坐标原点在水平面, 轴铅直向下 ,如果
设 所对应的薄层的体积为圆柱体体积, 那么在 上以直代曲,便得体积元素从而得到重力作功的功元素 .
(2) 分割 : 对 把区间 所对应的薄层的体积用圆柱体体积代替,得到
解: (1) 确定积分变量和积分区间:
建立如图所示的坐标系.
则半圆的方程为 取x为积分变量, 则
新知探究
由于将这一薄层水吸出是这一薄层水的重力在作功,设水的比重为 所以功的元素为
(3) 求定积分:将满池水全部抽出所作的功为
新知探究
1、
用铁锤把钉子钉入木板,设木板对铁钉的阻力与铁钉进入木板的深度成正比,铁锤在第一次锤击时将铁钉击入1厘米,若每次锤击所作的功相等,问第 次锤击时又将铁钉击入多少?
课堂练习
解:
设木板对铁钉的阻力为
第一次锤击时所作的功为
设 次击入的总深度为 厘米
次锤击所作的总功为
依题意知,每次锤击所作的功相等.
次击入的总深度为
第 次击入的深度为
2、
将直角边各为a及2a的直角三角形薄片垂直地浸入水中,斜边朝下,直角边的边长与水面平行,且该边到水面的距离恰等于该边的边长,求薄板所受的侧压力?
课堂练习
解:建立坐标系如图
面积微元
思考题
一球完全浸没水中,问该球面所受的总压力与球浸没的深度有无关系?它所受的总压力与它在水中受到的浮力有何关系?
3、
课堂练习
该球面所受的总压力方向向上(下半球面所受的压力大于上半球面),其值为该球排开水的重量,即球的体积,也就是它在水中受到的浮力.因此该球面所受的总压力与球浸没的深度无关.
一圆柱形蓄水池高为5米,底半径为3米,底半径为3米,池内盛满了水全部吸出,需作多少功?
4、
解:建立坐标系如图
这一薄层水的重力为
功元素为
(千焦).
讲解人:X X X 时间:20XX.XX.XX
PEOPLE'S EDUCATION PRESS HIGH SCHOOL MATHEMATICS ELECTIVE 2-2
感谢你的聆听
第1章 导数及其应用
人教版高中数学选修2-2
