第一章专题强化练1 带电粒子在有界匀强磁场中的运动练习(Word含解析)
文档属性
| 名称 | 第一章专题强化练1 带电粒子在有界匀强磁场中的运动练习(Word含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 164.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁科版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-12-04 06:12:03 | ||
图片预览



文档简介
第1章 安培力与洛伦兹力
专题强化练1 带电粒子在有界匀强磁场中的运动
一、选择题
1.(2021河北高二学业水平考试,)如图所示,边长为L的正方形区域abdc中,ab、cd位置放置两块平行金属板,初始时平行金属板不带电,区域内充满垂直纸面的匀强磁场(未画出),磁感应强度大小为B。一个质量为m,电荷量为q的带电粒子,以某速度从ac边中点垂直磁场方向射入,粒子垂直打到cd板上;撤去磁场,让金属板带上等量异种电荷,让该粒子从原位置以原速度射入电场,粒子打到ab板上的位置与a点间的距离为L。若电场、磁场同时存在,仍让粒子从原位置以原速度射入,不计粒子重力,则 ( )
A.粒子打在ab板上的位置距射入位置更远些
B.粒子打在cd板上的位置距射入位置更远些
C.粒子做曲线运动从板间飞出
D.粒子做匀速直线运动
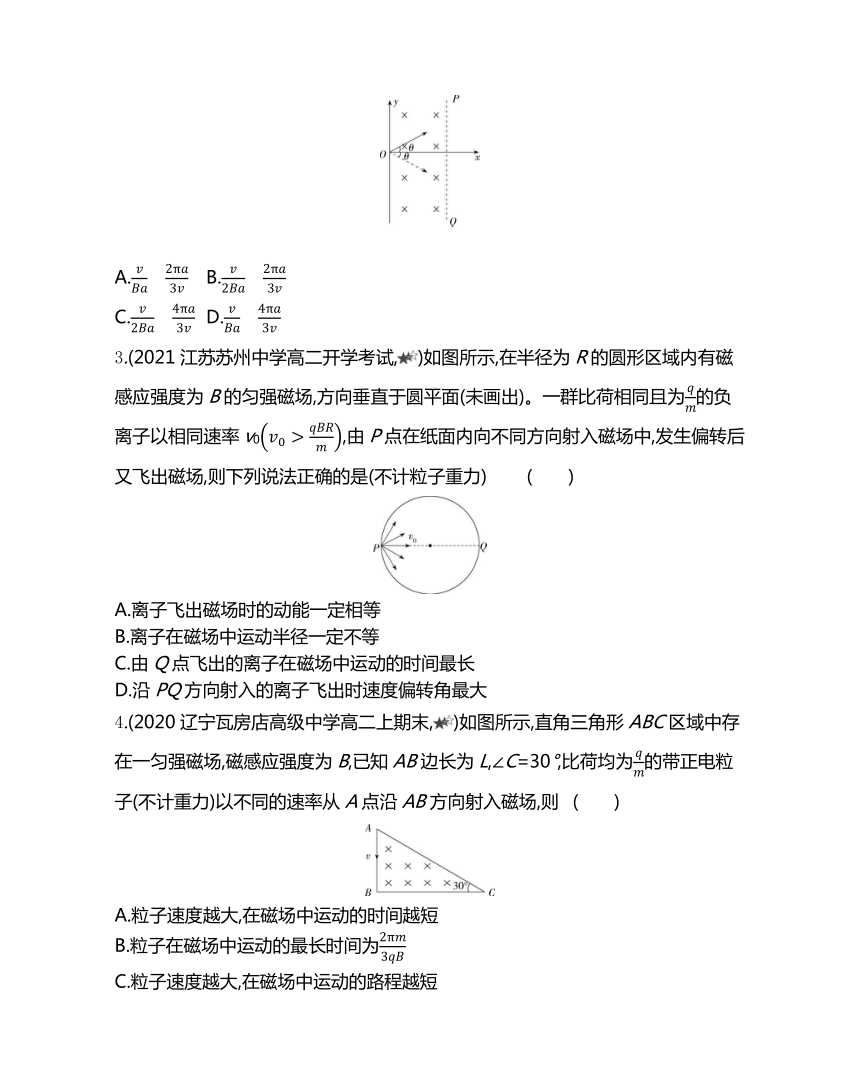
2.(2020山东潍坊高二上检测,)如图所示,直角坐标系中y轴右侧存在一垂直纸面向里、宽为a的有界匀强磁场,磁感应强度为B,右边界PQ平行于y轴,一粒子(重力不计)从原点O以与x轴正方向成θ角的速率v垂直射入磁场,当斜向上射入时,粒子恰好垂直PQ射出磁场,当斜向下射入时,粒子恰好不从右边界射出,则粒子的比荷及粒子恰好不从右边界射出时在磁场中运动的时间分别为 ( )
A. B.
C. D.
3.(2021江苏苏州中学高二开学考试,)如图所示,在半径为R的圆形区域内有磁感应强度为B的匀强磁场,方向垂直于圆平面(未画出)。一群比荷相同且为的负离子以相同速率v0,由P点在纸面内向不同方向射入磁场中,发生偏转后又飞出磁场,则下列说法正确的是(不计粒子重力) ( )
A.离子飞出磁场时的动能一定相等
B.离子在磁场中运动半径一定不等
C.由Q点飞出的离子在磁场中运动的时间最长
D.沿PQ方向射入的离子飞出时速度偏转角最大
4.(2020辽宁瓦房店高级中学高二上期末,)如图所示,直角三角形ABC区域中存在一匀强磁场,磁感应强度为B,已知AB边长为L,∠C=30°,比荷均为的带正电粒子(不计重力)以不同的速率从A点沿AB方向射入磁场,则 ( )
A.粒子速度越大,在磁场中运动的时间越短
B.粒子在磁场中运动的最长时间为
C.粒子速度越大,在磁场中运动的路程越短
D.粒子在磁场中运动的最长路程为πL
5.(2020四川蓉城名校联盟期末联考,)如图所示,两平行板间有垂直纸面向里的匀强磁场,磁感应强度为B,板长为L,两板间距离为L。有一个带电荷量为q、质量为m的粒子,以水平速度v从靠近上板边缘处进入该磁场,粒子恰能从下极板右侧边缘离开磁场,不计粒子重力。则 ( )
A.该粒子带正电
B.该粒子做匀变速曲线运动
C.该粒子在磁场中运动的时间为
D.该粒子离开磁场时速度偏转角为
6.(2021安徽临泉第一中学高二期末,)(多选)如图所示,边长为L的正方形区域内存在垂直纸面向里的匀强磁场。一个带电粒子静止在正方形的中心O处,某时刻该粒子分裂成两个带正电的粒子a、b,粒子a从中心O水平向左射出,经一段时间a、b两粒子同时射出磁场区域,已知粒子a恰从A处飞出磁场,粒子b从CD边某处飞出,飞出磁场时速度与CD边的夹角为60°。若忽略粒子重力和粒子间的相互作用力,则下列判断正确的是 ( )
A.a、b两带电粒子的运动半径之比为1∶2
B.a、b两带电粒子的速度大小之比为2∶3
C.a、b两带电粒子的质量之比为2∶3
D.a、b两带电粒子的比荷之比为2∶3
二、非选择题
7.(2021广东高三上八省联考模拟,)如图所示,在第一象限内有垂直于纸面向里的匀强磁场,磁感应强度为B,一个带正电的粒子质量为m,电荷量为q,由x轴上的P点垂直磁场射入,速度与x轴正方向夹角θ=45°,P点到坐标原点的距离为L,不计粒子的重力。
(1)若粒子恰好能从y轴上距原点L处的Q点飞出磁场,求粒子速度大小;
(2)若粒子在磁场中有最长的运动时间,求粒子速度大小的范围。
8.(2020江西高安中学高二上期末,)如图所示,在x轴的上方整个区域存在非匀强电场,PO之间的电压为U,在x轴的下方、半径为a的圆O1的区域内有垂直于xOy平面向外的匀强磁场,磁感应强度大小为B,其他区域无电场和磁场。现有带电粒子从P点由静止释放,沿y轴运动到O点,从O点进入磁场,经过一段时间后从N点离开磁场。已知∠OO1N=120°,不计带电粒子的重力与空气阻力。
(1)判断粒子的带电性质并比较P、O的电势高低;
(2)求带电粒子的比荷(电荷量与质量之比);
(3)若在粒子从O点运动到N点的过程中,某时刻磁感应强度大小突然变化为B',粒子不再离开磁场,求B'的最小值。
答案全解全析
第1章 安培力与洛伦兹力
专题强化练1 带电粒子在有界匀强磁场中的运动
1.D 粒子在磁场中做匀速圆周运动,轨道半径r==,得v=;粒子在电场中做类平抛运动,有L=vt,=·t2,得E=;当电场、磁场共同存在时,电场力F=Eq=,方向竖直向上,洛伦兹力F洛=qvB=,方向竖直向下,粒子所受合力为零,故粒子做匀速直线运动,选D。
2.C 粒子在磁场中运动轨迹如图所示,则由图知斜向上射入时有r sin θ=a,斜向下射入时有r sin θ+a=r,联立解得θ=30°,且r=2a,由洛伦兹力提供向心力得Bqv=m,解得r=,即粒子的比荷为=,粒子恰好不从右边界射出时在磁场中运动的圆心角为α=2×(90°-30°)=120°,运动时间为t==,选项C正确。
3.C 带电离子在磁场中运动时,洛伦兹力不做功,所以速度大小不发生变化,则射出时离子的动能不变,离子的动能Ek=m,虽然离子的比荷相同,但质量不一定相等,故离子飞出磁场时的动能不一定相等,A错误;离子在磁场中做匀速圆周运动,洛伦兹力提供向心力,由牛顿第二定律得qv0B=m,解得r=>R,因离子的速率相同,比荷相同,故运动半径一定相同,B错误;由圆的性质可知,轨迹圆半径一定时,当轨迹圆的弦长最大时,对应圆心角最大,速度偏转角最大,由于最长弦长为PQ,故由Q点飞出的离子对应的圆心角最大,运动时间最长,故C正确;由C选项的分析知道,从Q点飞出的粒子速度偏转角最大,此时离子一定不会沿PQ射入,故D错误。 故选C。
4.B 粒子在磁场中做匀速圆周运动,粒子可能由AC边射出,也可能由BC边射出,先分析从AC边射出的粒子,根据几何关系,这些粒子在磁场中偏转的圆心角相等,都为120°,根据粒子在磁场中运动的时间t=T,又因为粒子在磁场中做圆周运动的周期T=,所以粒子运动时间为t=×=,而从BC边射出的粒子在磁场中偏转的圆心角小于90°,所以A错误,B正确;粒子速度越大,根据公式r=可知半径越大,对于从AC边射出的粒子,速度越大,半径越大,对应的路程越长,C错误;当粒子轨迹与BC边相切时路程最长,根据几何知识可得此时的半径为r=L,则l=×r=L,D错误。
5.D 如图所示,粒子向下偏转,受洛伦兹力方向向下,故粒子带负电,A错误;带电粒子在匀强磁场中做匀速圆周运动,不是匀变速曲线运动,B错误;粒子在磁场中做匀速圆周运动的轨迹如图所示:
设粒子做圆周运动的半径为R,在磁场中运动转过的圆心角为θ,由图可知R2=(R-L)2+(L)2,解得R=2L,则sin θ=,圆心角为,运动时间为t==,由几何关系可知粒子离开磁场时速度偏角等于θ,即速度偏角为,选项C错误,D正确。
6.AC 由题意画出a、b两带电粒子在磁场中的运动轨迹如图所示,
由几何关系可知r2=2r1,所以a、b两带电粒子的运动半径之比为1∶2,A正确;由图可知a、b两带电粒子的运动时间为ta=Ta ,tb=Tb,由于ta=tb,则有Ta∶Tb=1∶3,根据周期公式T=可得a、b两带电粒子的比荷之比为3∶1,所以D错误;由动量守恒定律有mava=mbvb,根据半径公式有r=,则a、b两带电粒子的电荷量之比为2∶1,所以a、b两带电粒子的质量之比为2∶3,速度大小之比为3∶2,则B错误,则C正确。
7.答案 (1) (2)v≤
解析 (1)画出粒子在磁场中的轨迹如图甲所示:
设粒子速度为v1,有
qvB=m
由几何关系可得
r=L
解得v1=
(2)若粒子在磁场中运动时间最长,则应从x轴射出磁场,设其速度的最大值为v0, 此时粒子恰好与y轴相切,如图乙所示。由几何关系可知
r0+r0 cos 45°=L
解得r0=(2-)L
则v0=
故粒子的速度v≤。
8.答案 (1)粒子带正电 P的电势比O的高
(2) (3)(3+)B
解析 (1)粒子进入磁场向左偏转,根据左手定则,粒子带正电,在电场中被加速,所以P的电势比O的高;
(2)在电场中
qU=mv2,
在磁场中运动轨迹如图
由几何关系得运动半径
r=a,
由洛伦兹力提供向心力有
qvB=m,
联立解得
=;
(3)粒子不离开磁场时的运动轨迹如图所示
由几何关系可得不离开磁场运动的最大半径
rm=,
半径与磁感应强度成反比,故
Bmin=(3+)B。
专题强化练1 带电粒子在有界匀强磁场中的运动
一、选择题
1.(2021河北高二学业水平考试,)如图所示,边长为L的正方形区域abdc中,ab、cd位置放置两块平行金属板,初始时平行金属板不带电,区域内充满垂直纸面的匀强磁场(未画出),磁感应强度大小为B。一个质量为m,电荷量为q的带电粒子,以某速度从ac边中点垂直磁场方向射入,粒子垂直打到cd板上;撤去磁场,让金属板带上等量异种电荷,让该粒子从原位置以原速度射入电场,粒子打到ab板上的位置与a点间的距离为L。若电场、磁场同时存在,仍让粒子从原位置以原速度射入,不计粒子重力,则 ( )
A.粒子打在ab板上的位置距射入位置更远些
B.粒子打在cd板上的位置距射入位置更远些
C.粒子做曲线运动从板间飞出
D.粒子做匀速直线运动
2.(2020山东潍坊高二上检测,)如图所示,直角坐标系中y轴右侧存在一垂直纸面向里、宽为a的有界匀强磁场,磁感应强度为B,右边界PQ平行于y轴,一粒子(重力不计)从原点O以与x轴正方向成θ角的速率v垂直射入磁场,当斜向上射入时,粒子恰好垂直PQ射出磁场,当斜向下射入时,粒子恰好不从右边界射出,则粒子的比荷及粒子恰好不从右边界射出时在磁场中运动的时间分别为 ( )
A. B.
C. D.
3.(2021江苏苏州中学高二开学考试,)如图所示,在半径为R的圆形区域内有磁感应强度为B的匀强磁场,方向垂直于圆平面(未画出)。一群比荷相同且为的负离子以相同速率v0,由P点在纸面内向不同方向射入磁场中,发生偏转后又飞出磁场,则下列说法正确的是(不计粒子重力) ( )
A.离子飞出磁场时的动能一定相等
B.离子在磁场中运动半径一定不等
C.由Q点飞出的离子在磁场中运动的时间最长
D.沿PQ方向射入的离子飞出时速度偏转角最大
4.(2020辽宁瓦房店高级中学高二上期末,)如图所示,直角三角形ABC区域中存在一匀强磁场,磁感应强度为B,已知AB边长为L,∠C=30°,比荷均为的带正电粒子(不计重力)以不同的速率从A点沿AB方向射入磁场,则 ( )
A.粒子速度越大,在磁场中运动的时间越短
B.粒子在磁场中运动的最长时间为
C.粒子速度越大,在磁场中运动的路程越短
D.粒子在磁场中运动的最长路程为πL
5.(2020四川蓉城名校联盟期末联考,)如图所示,两平行板间有垂直纸面向里的匀强磁场,磁感应强度为B,板长为L,两板间距离为L。有一个带电荷量为q、质量为m的粒子,以水平速度v从靠近上板边缘处进入该磁场,粒子恰能从下极板右侧边缘离开磁场,不计粒子重力。则 ( )
A.该粒子带正电
B.该粒子做匀变速曲线运动
C.该粒子在磁场中运动的时间为
D.该粒子离开磁场时速度偏转角为
6.(2021安徽临泉第一中学高二期末,)(多选)如图所示,边长为L的正方形区域内存在垂直纸面向里的匀强磁场。一个带电粒子静止在正方形的中心O处,某时刻该粒子分裂成两个带正电的粒子a、b,粒子a从中心O水平向左射出,经一段时间a、b两粒子同时射出磁场区域,已知粒子a恰从A处飞出磁场,粒子b从CD边某处飞出,飞出磁场时速度与CD边的夹角为60°。若忽略粒子重力和粒子间的相互作用力,则下列判断正确的是 ( )
A.a、b两带电粒子的运动半径之比为1∶2
B.a、b两带电粒子的速度大小之比为2∶3
C.a、b两带电粒子的质量之比为2∶3
D.a、b两带电粒子的比荷之比为2∶3
二、非选择题
7.(2021广东高三上八省联考模拟,)如图所示,在第一象限内有垂直于纸面向里的匀强磁场,磁感应强度为B,一个带正电的粒子质量为m,电荷量为q,由x轴上的P点垂直磁场射入,速度与x轴正方向夹角θ=45°,P点到坐标原点的距离为L,不计粒子的重力。
(1)若粒子恰好能从y轴上距原点L处的Q点飞出磁场,求粒子速度大小;
(2)若粒子在磁场中有最长的运动时间,求粒子速度大小的范围。
8.(2020江西高安中学高二上期末,)如图所示,在x轴的上方整个区域存在非匀强电场,PO之间的电压为U,在x轴的下方、半径为a的圆O1的区域内有垂直于xOy平面向外的匀强磁场,磁感应强度大小为B,其他区域无电场和磁场。现有带电粒子从P点由静止释放,沿y轴运动到O点,从O点进入磁场,经过一段时间后从N点离开磁场。已知∠OO1N=120°,不计带电粒子的重力与空气阻力。
(1)判断粒子的带电性质并比较P、O的电势高低;
(2)求带电粒子的比荷(电荷量与质量之比);
(3)若在粒子从O点运动到N点的过程中,某时刻磁感应强度大小突然变化为B',粒子不再离开磁场,求B'的最小值。
答案全解全析
第1章 安培力与洛伦兹力
专题强化练1 带电粒子在有界匀强磁场中的运动
1.D 粒子在磁场中做匀速圆周运动,轨道半径r==,得v=;粒子在电场中做类平抛运动,有L=vt,=·t2,得E=;当电场、磁场共同存在时,电场力F=Eq=,方向竖直向上,洛伦兹力F洛=qvB=,方向竖直向下,粒子所受合力为零,故粒子做匀速直线运动,选D。
2.C 粒子在磁场中运动轨迹如图所示,则由图知斜向上射入时有r sin θ=a,斜向下射入时有r sin θ+a=r,联立解得θ=30°,且r=2a,由洛伦兹力提供向心力得Bqv=m,解得r=,即粒子的比荷为=,粒子恰好不从右边界射出时在磁场中运动的圆心角为α=2×(90°-30°)=120°,运动时间为t==,选项C正确。
3.C 带电离子在磁场中运动时,洛伦兹力不做功,所以速度大小不发生变化,则射出时离子的动能不变,离子的动能Ek=m,虽然离子的比荷相同,但质量不一定相等,故离子飞出磁场时的动能不一定相等,A错误;离子在磁场中做匀速圆周运动,洛伦兹力提供向心力,由牛顿第二定律得qv0B=m,解得r=>R,因离子的速率相同,比荷相同,故运动半径一定相同,B错误;由圆的性质可知,轨迹圆半径一定时,当轨迹圆的弦长最大时,对应圆心角最大,速度偏转角最大,由于最长弦长为PQ,故由Q点飞出的离子对应的圆心角最大,运动时间最长,故C正确;由C选项的分析知道,从Q点飞出的粒子速度偏转角最大,此时离子一定不会沿PQ射入,故D错误。 故选C。
4.B 粒子在磁场中做匀速圆周运动,粒子可能由AC边射出,也可能由BC边射出,先分析从AC边射出的粒子,根据几何关系,这些粒子在磁场中偏转的圆心角相等,都为120°,根据粒子在磁场中运动的时间t=T,又因为粒子在磁场中做圆周运动的周期T=,所以粒子运动时间为t=×=,而从BC边射出的粒子在磁场中偏转的圆心角小于90°,所以A错误,B正确;粒子速度越大,根据公式r=可知半径越大,对于从AC边射出的粒子,速度越大,半径越大,对应的路程越长,C错误;当粒子轨迹与BC边相切时路程最长,根据几何知识可得此时的半径为r=L,则l=×r=L,D错误。
5.D 如图所示,粒子向下偏转,受洛伦兹力方向向下,故粒子带负电,A错误;带电粒子在匀强磁场中做匀速圆周运动,不是匀变速曲线运动,B错误;粒子在磁场中做匀速圆周运动的轨迹如图所示:
设粒子做圆周运动的半径为R,在磁场中运动转过的圆心角为θ,由图可知R2=(R-L)2+(L)2,解得R=2L,则sin θ=,圆心角为,运动时间为t==,由几何关系可知粒子离开磁场时速度偏角等于θ,即速度偏角为,选项C错误,D正确。
6.AC 由题意画出a、b两带电粒子在磁场中的运动轨迹如图所示,
由几何关系可知r2=2r1,所以a、b两带电粒子的运动半径之比为1∶2,A正确;由图可知a、b两带电粒子的运动时间为ta=Ta ,tb=Tb,由于ta=tb,则有Ta∶Tb=1∶3,根据周期公式T=可得a、b两带电粒子的比荷之比为3∶1,所以D错误;由动量守恒定律有mava=mbvb,根据半径公式有r=,则a、b两带电粒子的电荷量之比为2∶1,所以a、b两带电粒子的质量之比为2∶3,速度大小之比为3∶2,则B错误,则C正确。
7.答案 (1) (2)v≤
解析 (1)画出粒子在磁场中的轨迹如图甲所示:
设粒子速度为v1,有
qvB=m
由几何关系可得
r=L
解得v1=
(2)若粒子在磁场中运动时间最长,则应从x轴射出磁场,设其速度的最大值为v0, 此时粒子恰好与y轴相切,如图乙所示。由几何关系可知
r0+r0 cos 45°=L
解得r0=(2-)L
则v0=
故粒子的速度v≤。
8.答案 (1)粒子带正电 P的电势比O的高
(2) (3)(3+)B
解析 (1)粒子进入磁场向左偏转,根据左手定则,粒子带正电,在电场中被加速,所以P的电势比O的高;
(2)在电场中
qU=mv2,
在磁场中运动轨迹如图
由几何关系得运动半径
r=a,
由洛伦兹力提供向心力有
qvB=m,
联立解得
=;
(3)粒子不离开磁场时的运动轨迹如图所示
由几何关系可得不离开磁场运动的最大半径
rm=,
半径与磁感应强度成反比,故
Bmin=(3+)B。
