人教高中数学必修四2.4.2-平面向量数量积的坐标表示、模、夹角-课件(18张ppt)
文档属性
| 名称 | 人教高中数学必修四2.4.2-平面向量数量积的坐标表示、模、夹角-课件(18张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 715.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-06 00:00:00 | ||
图片预览






文档简介
(共18张PPT)
2.4.2 平面向量数量积的坐标
表示、模、夹角
复习引入
1. 平面向量的数量积(内积)的定义:
2. 两个向量的数量积的性质:
3. 运算律:
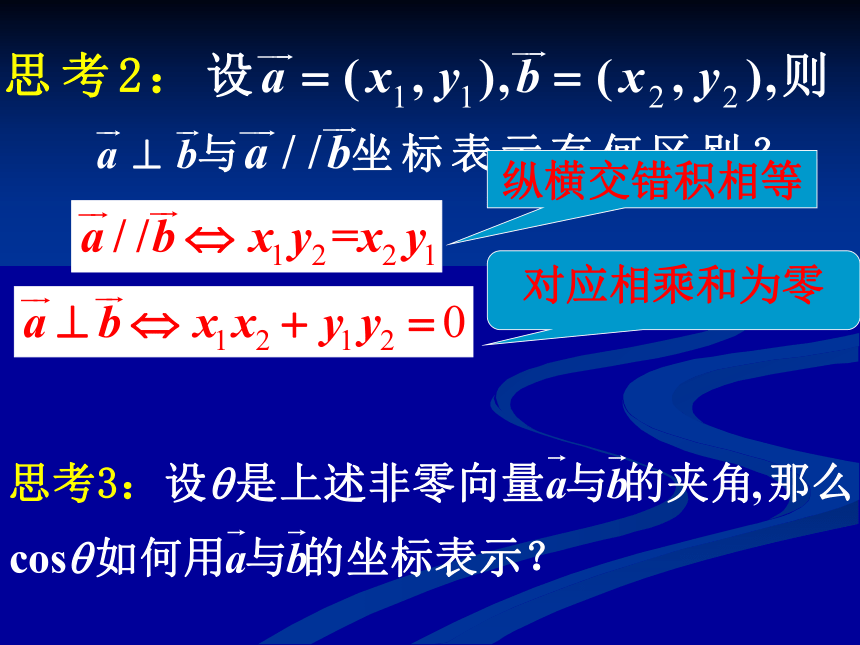
探究(一):平面向量数量积的坐标表示
探究(二):向量的模和夹角的坐标表示
纵横交错积相等
对应相乘和为零
三、应用巩固
例3:已知A(1、2),B(2,3),C( 2,5),求证ΔABC是直角三角形
证明:
∵AB = (2 1,3 2)= (1,1)
AC = ( 2 1,5 2)
= ( 3,3)
∴AB AC = 1╳( 3)+ 1╳ 3 = 0
∴AB⊥AC
∴ΔABC是直角三角形
注:两个向量的数量积是否为零是判断相应的两条直线是否垂直的重要方法之一。
A
B
C
O
X
Y
1、教材P107练习:1, 2
四、课堂练习
思考:
(1)已知 =(4,3),向量 是垂直于 的单位向量,求 .
小结与作业
小结:本节课学了什么?
作业:教材P108A组:5、6、7、10、11
5.已知a=(4,3),b=(-1,2).
(1)求a与b的夹角的余弦;
(2)若(a-λb)⊥(2a+b),求实数λ的值.
变式: 已知向量a=(λ,-2),b=(-3,5),若向量a 与b的夹角为钝角,求λ的取值范围.
4. 练习:
2.4.2 平面向量数量积的坐标
表示、模、夹角
复习引入
1. 平面向量的数量积(内积)的定义:
2. 两个向量的数量积的性质:
3. 运算律:
探究(一):平面向量数量积的坐标表示
探究(二):向量的模和夹角的坐标表示
纵横交错积相等
对应相乘和为零
三、应用巩固
例3:已知A(1、2),B(2,3),C( 2,5),求证ΔABC是直角三角形
证明:
∵AB = (2 1,3 2)= (1,1)
AC = ( 2 1,5 2)
= ( 3,3)
∴AB AC = 1╳( 3)+ 1╳ 3 = 0
∴AB⊥AC
∴ΔABC是直角三角形
注:两个向量的数量积是否为零是判断相应的两条直线是否垂直的重要方法之一。
A
B
C
O
X
Y
1、教材P107练习:1, 2
四、课堂练习
思考:
(1)已知 =(4,3),向量 是垂直于 的单位向量,求 .
小结与作业
小结:本节课学了什么?
作业:教材P108A组:5、6、7、10、11
5.已知a=(4,3),b=(-1,2).
(1)求a与b的夹角的余弦;
(2)若(a-λb)⊥(2a+b),求实数λ的值.
变式: 已知向量a=(λ,-2),b=(-3,5),若向量a 与b的夹角为钝角,求λ的取值范围.
4. 练习:
