2021-2022学年湘教版九年级数学下册2.3垂径定理 同步达标训练(word解析版)
文档属性
| 名称 | 2021-2022学年湘教版九年级数学下册2.3垂径定理 同步达标训练(word解析版) |

|
|
| 格式 | doc | ||
| 文件大小 | 466.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-05 00:00:00 | ||
图片预览




文档简介
2021-2022学年湘教版九年级数学下册《2.3垂径定理》同步达标训练(附答案)
1.我国著名的引滦工程的主干线输水管的截面如图所示,直径为2.6米,水最深为2.5米,则水面AB的宽为( )
A.0.9 米 B.1.0 米 C.1.1米 D.1.2米
2.如图,在5×5正方形网格中,一条圆弧经过A,B,C三点,已知点A的坐标是(﹣2,3),点C的坐标是(1,2),那么这条圆弧所在圆的圆心坐标是( )
A.(0,0) B.(﹣1,1) C.(﹣1,0) D.(﹣1,﹣1)
3.如图,3个正方形在⊙O直径的同侧,顶点B,C,G,H都在⊙O的直径上,正方形ABCD的顶点A在⊙O上,顶点D在PC上,正方形EFGH的顶点E在⊙O上,顶点F在QG上,正方形PCGQ的顶点P也在⊙O上,若BC=1,GH=2,则正方形PCGQ的面积为( )
A.5 B.6 C.7 D.10
4.如图,圆形纸片⊙O半径为,先在其内剪出2个边长相等的最大正方形,再在剩余部分剪出2个边长相等的最大正方形,则第二次剪出的正方形的边长是 .
5.如图,在半径为1的扇形AOB中,∠AOB=90°,点P是弧AB上任意一点(不与点A,B重合),OC⊥AP,OD⊥BP,垂足分别为C,D,则CD的长为 .
6.如图,在平面直角坐标系xOy中,以原点O为圆心的圆过点A(13,0),直线y=kx﹣3k+4(k≠0)与⊙O交于B、C两点,则弦BC的长的最小值为 .
7.如图,⊙O的直径为10,A、B、C、D是⊙O上四个动点,且AB=6,CD=8,若点E、F分别是弦AB、CD的中点,则线段EF的长度的取值范围是 .
8.如图,BC是⊙O的弦,以BC为边作等边三角形ABC,圆心O在△ABC的内部,若BC=6,OA=,则⊙O的半径为 .
9.如图所示,要把残破的轮片复制完整,已知弧上的三点A,B,C.
(1)用尺规作图法找出所在圆的圆心;(保留作图痕迹,不写作法)
(2)设△ABC是等腰三角形,底边BC=8cm,腰AB=5cm,求圆片的半径R.
10.已知:如图⊙O中,弦AB⊥CD,垂足为H,OG⊥BC,垂足为G,求证:弦AD=2OG.
11.如图,AB是⊙O的弦,C、D为直线AB上两点,OC=OD,求证:AC=BD.
12.如图,AB是⊙O的弦,半径OC、OD分别交AB于点E、F,AE=BF,请找出线段OE与OF的数量关系,并给予证明.
13.如图,两个圆都以点O为圆心,大圆的弦AB交小圆于C、D两点.
求证:AC=BD.
14.如图,某地有一座圆弧形拱桥,桥下水面宽度AB为12米,拱顶离水面的高CD为3米,现有一艘宽9米,船舱顶部为长方形,并且高出水面1.8米的货船要经过这里,此货船能顺利通过这座桥吗?(此图仅供参考)
15.如图,已知圆O的直径AB垂直于弦CD于点E,连接CO并延长交AD于点F,且CF⊥AD.
(1)证明:点E是OB的中点;
(2)若AE=8,求CD的长.
16.已知:如图,AB为⊙O的直径,OD∥AC.求证:点D平分.
17.如图,在正方形网格图中建立一直角坐标系,一条圆弧经过网格点A(0,2),B(4,2),C(6,0),解答下列问题:
(1)请在图中确定该圆弧所在圆心D点的位置,并写出D点坐标为 ;
(2)连接AD,CD,求⊙D的半径(结果保留根号).
18.如图所示,射线AM交一圆于点B,C,射线AN交该圆于点D,F,且BC=DE,求证:AC=AE.
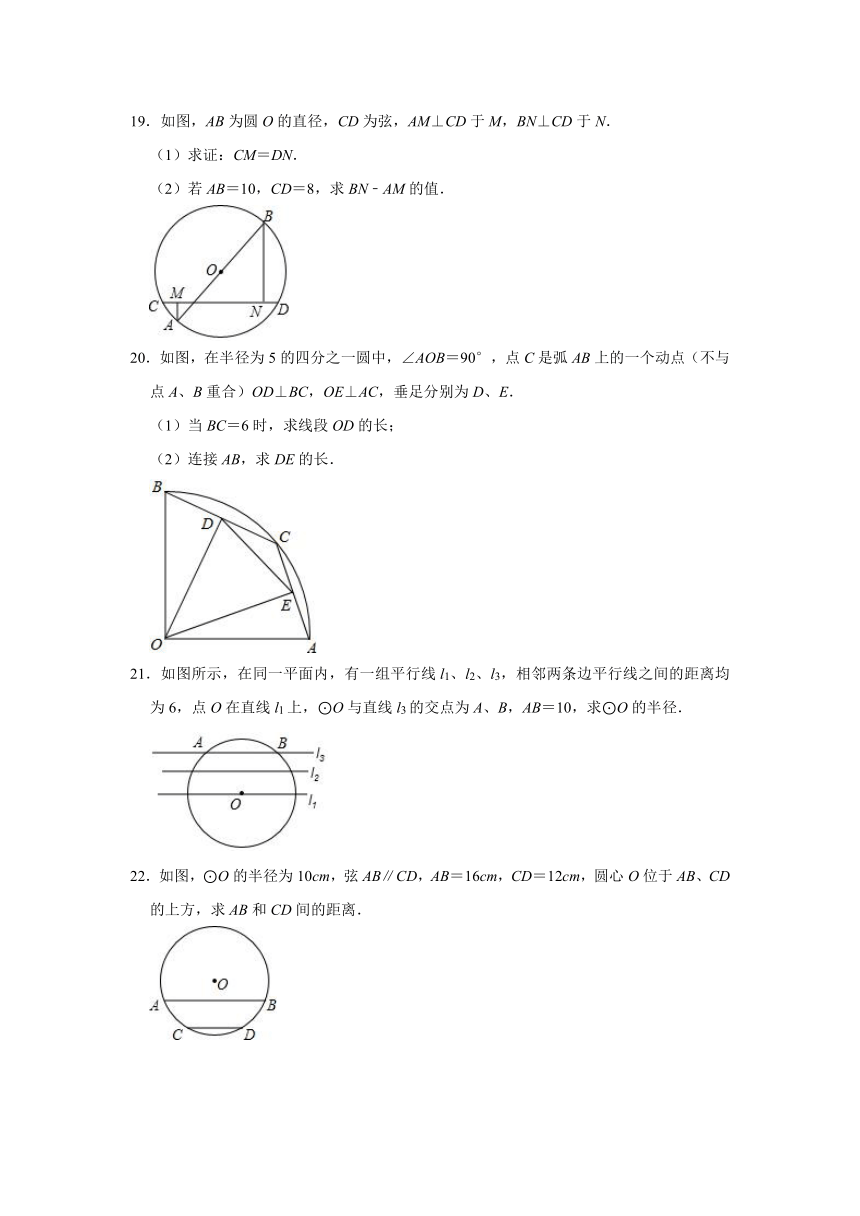
19.如图,AB为圆O的直径,CD为弦,AM⊥CD于M,BN⊥CD于N.
(1)求证:CM=DN.
(2)若AB=10,CD=8,求BN﹣AM的值.
20.如图,在半径为5的四分之一圆中,∠AOB=90°,点C是弧AB上的一个动点(不与点A、B重合)OD⊥BC,OE⊥AC,垂足分别为D、E.
(1)当BC=6时,求线段OD的长;
(2)连接AB,求DE的长.
21.如图所示,在同一平面内,有一组平行线l1、l2、l3,相邻两条边平行线之间的距离均为6,点O在直线l1上,⊙O与直线l3的交点为A、B,AB=10,求⊙O的半径.
22.如图,⊙O的半径为10cm,弦AB∥CD,AB=16cm,CD=12cm,圆心O位于AB、CD的上方,求AB和CD间的距离.
23.如图,∠P的两边分别与⊙O交于点A、B、C、D,且其平分线恰好过圆心O.求证:PA=PC.
24.如图,OA=OB,AB交⊙O于点C、D,AC与BD是否相等?为什么?
25.如图,⊙C经过原点且与两坐标轴分别交于点A和点B,点A的坐标为(0,2),D为⊙C在第一象限内的一点且∠ODB=60°,解答下列各题:
(1)求线段AB的长及⊙C的半径;
(2)求B点坐标及圆心C的坐标.
26.已知,∠EPF的角平分线上有一点O,以点O为圆心的圆与角的两边分别交于A,B和C,D.易证:AB=CD.
当点P在⊙O外(如图②),点P在⊙O内,(如图③)的位置时,请你猜想并写出AB与CD的数量关系?并选择其中一种情况加以证明.
参考答案
1.解:作OC⊥AB交圆于C,交AB于D,连接OA,
则OA=1.3,OD=1.2,
由勾股定理得,AD==0.5,
则AB=2AD=1.0(米),
故选:B.
2.解:如图线段AB的垂直平分线和线段CD的垂直平分线的交点M,
即圆心的坐标是(﹣1,1),
故选:B.
3.解:连接AO、PO、EO,设⊙O的半径为r,OC=x,OG=y,
由勾股定理可知:,
②﹣③得到:x2+(x+y)2﹣(y+2)2﹣22=0,
∴(x+y)2﹣22=(y+2)2﹣x2,
∴(x+y+2)(x+y﹣2)=(y+2+x)(y+2﹣x),
∵x+y+2≠0,
∴x+y﹣2=y+2﹣x,
∴x=2,代入①得到r2=10,代入②得到:10=4+(x+y)2,
∴(x+y)2=6,
∵x+y>0,
∴x+y=,
∴y=﹣2.
∴CG=x+y=,
∴正方形PCGQ的面积为6,
故选:B.
4.解:如图,连接AB、OE,过O作OF⊥DE于F,
则DF=EF,
设BC=x,DE=y,
由题意得:∠C=90°,AC=2BC=2x,
∴AB是直径,
∴AB=2OA=2,
在Rt△ABC中,由勾股定理得:x2+(2x)2=(2)2,
解得:x=2,
则BC=2,
在Rt△OEF中,由勾股定理得:(×2+y)2+(y)2=()2,
解得:y=(负值已舍去),
即第二次剪出的正方形的边长是,
故答案为:.
5.解:连接AB,如图,
∵OA=OB=1,∠AOB=90°,
∴AB=OA=,
∵OC⊥AP,OD⊥BP,
∴AC=PC,BD=PD,
∴CD为△PAB的中位线,
∴CD=AB=.
故答案为.
6.解:连接OB,
∵直线y=kx﹣3k+4必过点D(3,4),
∴最短的弦CB是过点D且与该圆直径垂直的弦,
∵点D的坐标是(3,4),
∴OD==5,
∵以原点O为圆心的圆过点A(13,0),
∴圆的半径为13,
∴OB=13,
∴BD===12,
∴BC=2BD=24,
∴BC的长的最小值为24;
故答案为:24.
7.解:连接OE、OF、OA、OC,如图所示:
∵⊙O的直径为10,
∴OA=OC=5,
∵点E、F分别是弦AB、CD的中点,AB=6,CD=8,
∴OE⊥AB,OF⊥CD,AE=AB=3,CF=CD=4,
∴OE===4,OF===3,
当AB∥CD时,E、O、F三点共线,
当AB、CD位于O的同侧时,线段EF的长度最短=OE﹣OF=1,
当AB、CD位于O的两侧时,线段EF的长度最长=OE+OF=7,
∴线段EF的长度的取值范围是1≤EF≤7,
故答案为:1≤EF≤7.
8.解:过O作OD⊥BC于D,连接OB,
∵BC是⊙O的一条弦,且BC=6,
∴BD=CD=BC=×6=3,
∴OD垂直平分BC,又AB=AC,
∴点A在BC的垂直平分线上,即A,O及D三点共线,
∵△ABC是等边三角形,
∴∠ABC=60°,
∴AD=BD=3,
∵OA=,
∴OD=AD﹣OA=2
在Rt△OBD中,OB===;
故答案为:.
9.解:(1)作法:分别作AB和AC的垂直平分线,设交点为O,则O为所求圆的圆心;
(2)连接AO、BO,AO交BC于E,
∵AB=AC,
∴AE⊥BC,
∴BE=BC=×8=4,
在Rt△ABE中,AE===3,
设⊙O的半径为R,在Rt△BEO中,
OB2=BE2+OE2,
即R2=42+(R﹣3)2,
R=,
答:圆片的半径R为cm.
10.证明:作直径CM,连接BM,DM,AM,
∵OG⊥BC,OG过O,
∴CG=BG,
∵CO=OM,
∴BM=2OG,
∵CM为⊙O直径,
∴∠CDM=90°,
∵AB⊥CD,
∴∠CHB=90°,
∴∠CHB=∠CDM,
∴AB∥DM,
∴∠BAM=∠AMD,
∴AD=BM,
∴AD=2OG.
11.证明:作OH⊥AB于H,如图,
则AH=BH,
∵OC=OD,OH⊥AB,
∴CH=DH,
∴CH﹣AH=DH﹣BH,
即AC=BD.
12.解:OE=OF
理由如下:过点O作OH⊥AB于点H,
∵OH过圆心,OH⊥AB
∴AH=BH,
又∵AE=BF
∴AH﹣AE=BH﹣BE
即EH=FH,
∵EH=FH,OH⊥EF
∴OH垂直平分EF,
∴OE=OF.
13.证明:过点O作OE⊥AB,
∵OA=OB,
∴AE=BE,
又∵在⊙O中,
∴CE=DE,
∴AC=BD
14.解:货船不能顺利通过这座拱桥.理由:
连接OA,
根据题意得:CD=3米,AB=12米,
则AD=AB=6(米),
设这座拱桥所在圆的半径为x米,
则OA=OC=x米,OD=OC﹣CD=(x﹣3)米,
在Rt△AOD中,OA2=OD2+AD2,
则x2=(x﹣3)2+62,
解得:x=7.5,
连接OM,
设MN=9米,
∵OC⊥MN,
∴MH=MN=4.5(米),
在Rt△OMH中,OH==6(米),
∵OD=OC﹣CD=7.5﹣3=4.5(米)
∵OH﹣OD=6﹣4.5=1.5(米)<1.8米,
∴货船不能顺利通过这座拱桥.
15.(1)证明:连接AC,如图,
∵直径AB垂直于弦CD于点E,
∴=,
∴AC=AD,
∵过圆心O的线段CF⊥AD,
∴AF=DF,即CF是AD的中垂线,
∴AC=CD,
∴AC=AD=CD.
即△ACD是等边三角形,
∴∠FCD=30°,
在Rt△COE中,OE=OC,
∴OE=OB,
∴点E为OB的中点;
(2)解:∵△ACD是等边三角形,AB⊥CD,
∴∠CAE=30°,
∴CE=AE×tan30°=8×=,
∵直径AB垂直于弦CD于点E,
∴CD=2CE=.
16.证明:连接CB,
∵AB为⊙O的直径,
∴∠ACB=90°,
∵OD∥AC,
∴∠OEB=∠ACB=90°,
即OD⊥BC,
∵OD过O,
∴点D平分.
17.解:(1)如图1,∵圆弧经过网格点A(0,2),B(4,2),
∴圆心的横坐标为2,
作BC的垂直平分线与AB的垂直平分线交于D,
则D(2,﹣2),
故答案为:(2,﹣2);
(2)如图2,过点D作DE⊥y轴,交y轴于点E,
在Rt△ADE中,AE=4,DE=2,
则r==2,
所以⊙D的半径为2.
18.证明:作OP⊥AC于P,OQ⊥AE于Q,连接OB、OD、OA,则PB=BC,DQ=DE,
∵BC=DE,
∴PB=DQ,PC=QE,
在RT△OPB和RT△OQD中,
,
∴RT△OPB≌RT△OQD(HL),
∴OP=OQ,
在RT△OPA和RT△OQA中,
,
∴RT△OPA≌RT△OQA(HL),
∴AP=AQ,
∴AP+PC=AQ+QE,
即AC=AE.
19.(1)证明:过O作OF⊥CD于F,
∵AM⊥CD于M,BN⊥CD于N,
∴AM∥FO∥NB,
∵OA=OB,
∴MF=NF,
∵OF⊥CD,O为圆心,
∴CF=FD,
∴CF﹣MF=FD﹣FN,即MC=ND;
(2)解:连接OD,
∵AB=10,CD=8,
∴OD=5,FD=4,
∴OF=3,
设OE=x,则EB=x+5,AE=5﹣x,
∵NB∥FO,
∴△EBN∽△EOF,
∴=,即BN:3=(5+x):x,
∴BN=,①
∵MA∥FO,
∴△AME∽△OFE,
∴AM:3=(5﹣x):x,
∴AM=②
两式相减即可得到,BN﹣AM=6.
20.解:(1)如图(1),
∵OD⊥BC,
∴BD=BC=×6=3,
∵∠BDO=90°,OB=5,BD=3,
∴OD==4,
即线段OD的长为4.
(2)如图(2),
∵∠AOB=90°,OA=OB=5,
∴AB==5,
∵OD⊥BC,OE⊥AC,
∴D和E分别是线段BC和AC的中点,
∴DE=AB=.
21.解:过O作OD⊥AB于D,则AD=5,OD=12,
连接OA,
由勾股定理得:
OA=,
∴⊙O的直径为26.
22.解:过点O作弦AB的垂线,垂足为E,延长OE交CD于点F,连接OA,OC,
∵AB∥CD,
∴OF⊥CD,
∵AB=16cm,CD=12cm,
∴AE=AB=×16=8cm,CF=CD=×12=6cm,
在Rt△AOE中,
OE===6cm,
在Rt△OCF中,
OF===8cm,
∴EF=OF﹣OE=8﹣6=2cm.
答:AB和CD的距离为2cm.
23.证明:作OE⊥PB于E,OF⊥PD于F,
∴AE=EB,CF=FD,
∵OP平分∠BPD,OE⊥PB,OF⊥PD,
∴OE=OF,
∴AB=CD,
∴AE=CF,
在△POE和△POF中,
,
∴△POE≌△POF,
∴PE=PF,
∴PE﹣AE=PF﹣CF,即PA=PC.
24.解:AC=BD,理由为:
证明:过O作OE⊥CD,∴E为CD的中点,即CE=DE,
又OA=OB,OE⊥AB,
∴E为AB的中点,即AE=BE,
∴AE﹣CE=BE﹣DE,即AC=BD.
25.解:(1)连接AB;∵∠ODB=∠OAB,∠ODB=60°
∴∠OAB=60°,
∵∠AOB是直角,
∴AB是⊙C的直径,∠OBA=30°;
∴AB=2OA=4,∴⊙C的半径r=2;(5分)
(2)在Rt△OAB中,由勾股定理得:OB2+OA2=AB2,
∴OB=,∴B的坐标为:(,0)(8分)
过C点作CE⊥OA于E,CF⊥OB于F,
由垂径定理得:OE=AE=1,OF=BF=,
∴CE=,CF=1,
∴C的坐标为(,1).(12分)
26.解:AB=CD.理由如下:
对于图②:作OG⊥AB于G,OH⊥CD于H,连接OB、OD,则AG=BG,CH=DH,
∵PO平分∠EPF,
∴OG=OH,
在Rt△OBG和△ODH中,
,
∴Rt△OBG≌Rt△ODH(HL),
∴BG=DH,
∴AB=CD;
对于图③:作OG⊥AB于G,OH⊥CD于H,则AG=GB,CH=HD,证明的方法与图②一样.
1.我国著名的引滦工程的主干线输水管的截面如图所示,直径为2.6米,水最深为2.5米,则水面AB的宽为( )
A.0.9 米 B.1.0 米 C.1.1米 D.1.2米
2.如图,在5×5正方形网格中,一条圆弧经过A,B,C三点,已知点A的坐标是(﹣2,3),点C的坐标是(1,2),那么这条圆弧所在圆的圆心坐标是( )
A.(0,0) B.(﹣1,1) C.(﹣1,0) D.(﹣1,﹣1)
3.如图,3个正方形在⊙O直径的同侧,顶点B,C,G,H都在⊙O的直径上,正方形ABCD的顶点A在⊙O上,顶点D在PC上,正方形EFGH的顶点E在⊙O上,顶点F在QG上,正方形PCGQ的顶点P也在⊙O上,若BC=1,GH=2,则正方形PCGQ的面积为( )
A.5 B.6 C.7 D.10
4.如图,圆形纸片⊙O半径为,先在其内剪出2个边长相等的最大正方形,再在剩余部分剪出2个边长相等的最大正方形,则第二次剪出的正方形的边长是 .
5.如图,在半径为1的扇形AOB中,∠AOB=90°,点P是弧AB上任意一点(不与点A,B重合),OC⊥AP,OD⊥BP,垂足分别为C,D,则CD的长为 .
6.如图,在平面直角坐标系xOy中,以原点O为圆心的圆过点A(13,0),直线y=kx﹣3k+4(k≠0)与⊙O交于B、C两点,则弦BC的长的最小值为 .
7.如图,⊙O的直径为10,A、B、C、D是⊙O上四个动点,且AB=6,CD=8,若点E、F分别是弦AB、CD的中点,则线段EF的长度的取值范围是 .
8.如图,BC是⊙O的弦,以BC为边作等边三角形ABC,圆心O在△ABC的内部,若BC=6,OA=,则⊙O的半径为 .
9.如图所示,要把残破的轮片复制完整,已知弧上的三点A,B,C.
(1)用尺规作图法找出所在圆的圆心;(保留作图痕迹,不写作法)
(2)设△ABC是等腰三角形,底边BC=8cm,腰AB=5cm,求圆片的半径R.
10.已知:如图⊙O中,弦AB⊥CD,垂足为H,OG⊥BC,垂足为G,求证:弦AD=2OG.
11.如图,AB是⊙O的弦,C、D为直线AB上两点,OC=OD,求证:AC=BD.
12.如图,AB是⊙O的弦,半径OC、OD分别交AB于点E、F,AE=BF,请找出线段OE与OF的数量关系,并给予证明.
13.如图,两个圆都以点O为圆心,大圆的弦AB交小圆于C、D两点.
求证:AC=BD.
14.如图,某地有一座圆弧形拱桥,桥下水面宽度AB为12米,拱顶离水面的高CD为3米,现有一艘宽9米,船舱顶部为长方形,并且高出水面1.8米的货船要经过这里,此货船能顺利通过这座桥吗?(此图仅供参考)
15.如图,已知圆O的直径AB垂直于弦CD于点E,连接CO并延长交AD于点F,且CF⊥AD.
(1)证明:点E是OB的中点;
(2)若AE=8,求CD的长.
16.已知:如图,AB为⊙O的直径,OD∥AC.求证:点D平分.
17.如图,在正方形网格图中建立一直角坐标系,一条圆弧经过网格点A(0,2),B(4,2),C(6,0),解答下列问题:
(1)请在图中确定该圆弧所在圆心D点的位置,并写出D点坐标为 ;
(2)连接AD,CD,求⊙D的半径(结果保留根号).
18.如图所示,射线AM交一圆于点B,C,射线AN交该圆于点D,F,且BC=DE,求证:AC=AE.
19.如图,AB为圆O的直径,CD为弦,AM⊥CD于M,BN⊥CD于N.
(1)求证:CM=DN.
(2)若AB=10,CD=8,求BN﹣AM的值.
20.如图,在半径为5的四分之一圆中,∠AOB=90°,点C是弧AB上的一个动点(不与点A、B重合)OD⊥BC,OE⊥AC,垂足分别为D、E.
(1)当BC=6时,求线段OD的长;
(2)连接AB,求DE的长.
21.如图所示,在同一平面内,有一组平行线l1、l2、l3,相邻两条边平行线之间的距离均为6,点O在直线l1上,⊙O与直线l3的交点为A、B,AB=10,求⊙O的半径.
22.如图,⊙O的半径为10cm,弦AB∥CD,AB=16cm,CD=12cm,圆心O位于AB、CD的上方,求AB和CD间的距离.
23.如图,∠P的两边分别与⊙O交于点A、B、C、D,且其平分线恰好过圆心O.求证:PA=PC.
24.如图,OA=OB,AB交⊙O于点C、D,AC与BD是否相等?为什么?
25.如图,⊙C经过原点且与两坐标轴分别交于点A和点B,点A的坐标为(0,2),D为⊙C在第一象限内的一点且∠ODB=60°,解答下列各题:
(1)求线段AB的长及⊙C的半径;
(2)求B点坐标及圆心C的坐标.
26.已知,∠EPF的角平分线上有一点O,以点O为圆心的圆与角的两边分别交于A,B和C,D.易证:AB=CD.
当点P在⊙O外(如图②),点P在⊙O内,(如图③)的位置时,请你猜想并写出AB与CD的数量关系?并选择其中一种情况加以证明.
参考答案
1.解:作OC⊥AB交圆于C,交AB于D,连接OA,
则OA=1.3,OD=1.2,
由勾股定理得,AD==0.5,
则AB=2AD=1.0(米),
故选:B.
2.解:如图线段AB的垂直平分线和线段CD的垂直平分线的交点M,
即圆心的坐标是(﹣1,1),
故选:B.
3.解:连接AO、PO、EO,设⊙O的半径为r,OC=x,OG=y,
由勾股定理可知:,
②﹣③得到:x2+(x+y)2﹣(y+2)2﹣22=0,
∴(x+y)2﹣22=(y+2)2﹣x2,
∴(x+y+2)(x+y﹣2)=(y+2+x)(y+2﹣x),
∵x+y+2≠0,
∴x+y﹣2=y+2﹣x,
∴x=2,代入①得到r2=10,代入②得到:10=4+(x+y)2,
∴(x+y)2=6,
∵x+y>0,
∴x+y=,
∴y=﹣2.
∴CG=x+y=,
∴正方形PCGQ的面积为6,
故选:B.
4.解:如图,连接AB、OE,过O作OF⊥DE于F,
则DF=EF,
设BC=x,DE=y,
由题意得:∠C=90°,AC=2BC=2x,
∴AB是直径,
∴AB=2OA=2,
在Rt△ABC中,由勾股定理得:x2+(2x)2=(2)2,
解得:x=2,
则BC=2,
在Rt△OEF中,由勾股定理得:(×2+y)2+(y)2=()2,
解得:y=(负值已舍去),
即第二次剪出的正方形的边长是,
故答案为:.
5.解:连接AB,如图,
∵OA=OB=1,∠AOB=90°,
∴AB=OA=,
∵OC⊥AP,OD⊥BP,
∴AC=PC,BD=PD,
∴CD为△PAB的中位线,
∴CD=AB=.
故答案为.
6.解:连接OB,
∵直线y=kx﹣3k+4必过点D(3,4),
∴最短的弦CB是过点D且与该圆直径垂直的弦,
∵点D的坐标是(3,4),
∴OD==5,
∵以原点O为圆心的圆过点A(13,0),
∴圆的半径为13,
∴OB=13,
∴BD===12,
∴BC=2BD=24,
∴BC的长的最小值为24;
故答案为:24.
7.解:连接OE、OF、OA、OC,如图所示:
∵⊙O的直径为10,
∴OA=OC=5,
∵点E、F分别是弦AB、CD的中点,AB=6,CD=8,
∴OE⊥AB,OF⊥CD,AE=AB=3,CF=CD=4,
∴OE===4,OF===3,
当AB∥CD时,E、O、F三点共线,
当AB、CD位于O的同侧时,线段EF的长度最短=OE﹣OF=1,
当AB、CD位于O的两侧时,线段EF的长度最长=OE+OF=7,
∴线段EF的长度的取值范围是1≤EF≤7,
故答案为:1≤EF≤7.
8.解:过O作OD⊥BC于D,连接OB,
∵BC是⊙O的一条弦,且BC=6,
∴BD=CD=BC=×6=3,
∴OD垂直平分BC,又AB=AC,
∴点A在BC的垂直平分线上,即A,O及D三点共线,
∵△ABC是等边三角形,
∴∠ABC=60°,
∴AD=BD=3,
∵OA=,
∴OD=AD﹣OA=2
在Rt△OBD中,OB===;
故答案为:.
9.解:(1)作法:分别作AB和AC的垂直平分线,设交点为O,则O为所求圆的圆心;
(2)连接AO、BO,AO交BC于E,
∵AB=AC,
∴AE⊥BC,
∴BE=BC=×8=4,
在Rt△ABE中,AE===3,
设⊙O的半径为R,在Rt△BEO中,
OB2=BE2+OE2,
即R2=42+(R﹣3)2,
R=,
答:圆片的半径R为cm.
10.证明:作直径CM,连接BM,DM,AM,
∵OG⊥BC,OG过O,
∴CG=BG,
∵CO=OM,
∴BM=2OG,
∵CM为⊙O直径,
∴∠CDM=90°,
∵AB⊥CD,
∴∠CHB=90°,
∴∠CHB=∠CDM,
∴AB∥DM,
∴∠BAM=∠AMD,
∴AD=BM,
∴AD=2OG.
11.证明:作OH⊥AB于H,如图,
则AH=BH,
∵OC=OD,OH⊥AB,
∴CH=DH,
∴CH﹣AH=DH﹣BH,
即AC=BD.
12.解:OE=OF
理由如下:过点O作OH⊥AB于点H,
∵OH过圆心,OH⊥AB
∴AH=BH,
又∵AE=BF
∴AH﹣AE=BH﹣BE
即EH=FH,
∵EH=FH,OH⊥EF
∴OH垂直平分EF,
∴OE=OF.
13.证明:过点O作OE⊥AB,
∵OA=OB,
∴AE=BE,
又∵在⊙O中,
∴CE=DE,
∴AC=BD
14.解:货船不能顺利通过这座拱桥.理由:
连接OA,
根据题意得:CD=3米,AB=12米,
则AD=AB=6(米),
设这座拱桥所在圆的半径为x米,
则OA=OC=x米,OD=OC﹣CD=(x﹣3)米,
在Rt△AOD中,OA2=OD2+AD2,
则x2=(x﹣3)2+62,
解得:x=7.5,
连接OM,
设MN=9米,
∵OC⊥MN,
∴MH=MN=4.5(米),
在Rt△OMH中,OH==6(米),
∵OD=OC﹣CD=7.5﹣3=4.5(米)
∵OH﹣OD=6﹣4.5=1.5(米)<1.8米,
∴货船不能顺利通过这座拱桥.
15.(1)证明:连接AC,如图,
∵直径AB垂直于弦CD于点E,
∴=,
∴AC=AD,
∵过圆心O的线段CF⊥AD,
∴AF=DF,即CF是AD的中垂线,
∴AC=CD,
∴AC=AD=CD.
即△ACD是等边三角形,
∴∠FCD=30°,
在Rt△COE中,OE=OC,
∴OE=OB,
∴点E为OB的中点;
(2)解:∵△ACD是等边三角形,AB⊥CD,
∴∠CAE=30°,
∴CE=AE×tan30°=8×=,
∵直径AB垂直于弦CD于点E,
∴CD=2CE=.
16.证明:连接CB,
∵AB为⊙O的直径,
∴∠ACB=90°,
∵OD∥AC,
∴∠OEB=∠ACB=90°,
即OD⊥BC,
∵OD过O,
∴点D平分.
17.解:(1)如图1,∵圆弧经过网格点A(0,2),B(4,2),
∴圆心的横坐标为2,
作BC的垂直平分线与AB的垂直平分线交于D,
则D(2,﹣2),
故答案为:(2,﹣2);
(2)如图2,过点D作DE⊥y轴,交y轴于点E,
在Rt△ADE中,AE=4,DE=2,
则r==2,
所以⊙D的半径为2.
18.证明:作OP⊥AC于P,OQ⊥AE于Q,连接OB、OD、OA,则PB=BC,DQ=DE,
∵BC=DE,
∴PB=DQ,PC=QE,
在RT△OPB和RT△OQD中,
,
∴RT△OPB≌RT△OQD(HL),
∴OP=OQ,
在RT△OPA和RT△OQA中,
,
∴RT△OPA≌RT△OQA(HL),
∴AP=AQ,
∴AP+PC=AQ+QE,
即AC=AE.
19.(1)证明:过O作OF⊥CD于F,
∵AM⊥CD于M,BN⊥CD于N,
∴AM∥FO∥NB,
∵OA=OB,
∴MF=NF,
∵OF⊥CD,O为圆心,
∴CF=FD,
∴CF﹣MF=FD﹣FN,即MC=ND;
(2)解:连接OD,
∵AB=10,CD=8,
∴OD=5,FD=4,
∴OF=3,
设OE=x,则EB=x+5,AE=5﹣x,
∵NB∥FO,
∴△EBN∽△EOF,
∴=,即BN:3=(5+x):x,
∴BN=,①
∵MA∥FO,
∴△AME∽△OFE,
∴AM:3=(5﹣x):x,
∴AM=②
两式相减即可得到,BN﹣AM=6.
20.解:(1)如图(1),
∵OD⊥BC,
∴BD=BC=×6=3,
∵∠BDO=90°,OB=5,BD=3,
∴OD==4,
即线段OD的长为4.
(2)如图(2),
∵∠AOB=90°,OA=OB=5,
∴AB==5,
∵OD⊥BC,OE⊥AC,
∴D和E分别是线段BC和AC的中点,
∴DE=AB=.
21.解:过O作OD⊥AB于D,则AD=5,OD=12,
连接OA,
由勾股定理得:
OA=,
∴⊙O的直径为26.
22.解:过点O作弦AB的垂线,垂足为E,延长OE交CD于点F,连接OA,OC,
∵AB∥CD,
∴OF⊥CD,
∵AB=16cm,CD=12cm,
∴AE=AB=×16=8cm,CF=CD=×12=6cm,
在Rt△AOE中,
OE===6cm,
在Rt△OCF中,
OF===8cm,
∴EF=OF﹣OE=8﹣6=2cm.
答:AB和CD的距离为2cm.
23.证明:作OE⊥PB于E,OF⊥PD于F,
∴AE=EB,CF=FD,
∵OP平分∠BPD,OE⊥PB,OF⊥PD,
∴OE=OF,
∴AB=CD,
∴AE=CF,
在△POE和△POF中,
,
∴△POE≌△POF,
∴PE=PF,
∴PE﹣AE=PF﹣CF,即PA=PC.
24.解:AC=BD,理由为:
证明:过O作OE⊥CD,∴E为CD的中点,即CE=DE,
又OA=OB,OE⊥AB,
∴E为AB的中点,即AE=BE,
∴AE﹣CE=BE﹣DE,即AC=BD.
25.解:(1)连接AB;∵∠ODB=∠OAB,∠ODB=60°
∴∠OAB=60°,
∵∠AOB是直角,
∴AB是⊙C的直径,∠OBA=30°;
∴AB=2OA=4,∴⊙C的半径r=2;(5分)
(2)在Rt△OAB中,由勾股定理得:OB2+OA2=AB2,
∴OB=,∴B的坐标为:(,0)(8分)
过C点作CE⊥OA于E,CF⊥OB于F,
由垂径定理得:OE=AE=1,OF=BF=,
∴CE=,CF=1,
∴C的坐标为(,1).(12分)
26.解:AB=CD.理由如下:
对于图②:作OG⊥AB于G,OH⊥CD于H,连接OB、OD,则AG=BG,CH=DH,
∵PO平分∠EPF,
∴OG=OH,
在Rt△OBG和△ODH中,
,
∴Rt△OBG≌Rt△ODH(HL),
∴BG=DH,
∴AB=CD;
对于图③:作OG⊥AB于G,OH⊥CD于H,则AG=GB,CH=HD,证明的方法与图②一样.
