2021-2022学年北师大版九年级数学下册2.4二次函数的应用同步达标测评(word解析版)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学下册2.4二次函数的应用同步达标测评(word解析版) |

|
|
| 格式 | doc | ||
| 文件大小 | 341.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-05 00:00:00 | ||
图片预览



文档简介
2021-2022学年北师大版九年级数学下册《2.4二次函数的应用》同步达标测评(附答案)
一.选择题(共9小题,满分27分)
1.如图是抛物线形的拱桥,当水面宽4m时,顶点离水面2m,当水面宽度增加到6m时,水面下降( )
A.1m B.1.5m C.2.5m D.2m
2.某超市销售一种商品,每件成本为50元,销售人员经调查发现,该商品每月的销售量y(件)与销售单价x(元)之间满足函数关系式y=﹣5x+550,若要求销售单价不得低于成本,为了每月所获利润最大,该商品销售单价应定为多少元?每月最大利润是多少?( )
A.90元,4500元 B.80元,4500元
C.90元,4000元 D.80元,4000元
3.某商品的进价为每件20元,现在的售价为每件40元,每星期可卖出200件.市场调查反映:如调整价格,每涨价1元,每星期要少卖出5件.则每星期售出商品的利润y(单位:元)与每件涨价x(单位:元)之间的函数关系式是( )
A.y=(200﹣5x)(40﹣20+x) B.y=(200+5x)(40﹣20﹣x)
C.y=200(40﹣20﹣x) D.y=200﹣5x
4.一次足球训练中,小明从球门正前方将球射向球门,球射向球门的路线呈抛物线.当球飞行的水平距离为6m时,球达到最高点,此时球离地面3m.已知球门高是2.44m,若足球能射入球门,则小明与球门的距离可能是( )
A.10m B.8m C.6m D.5m
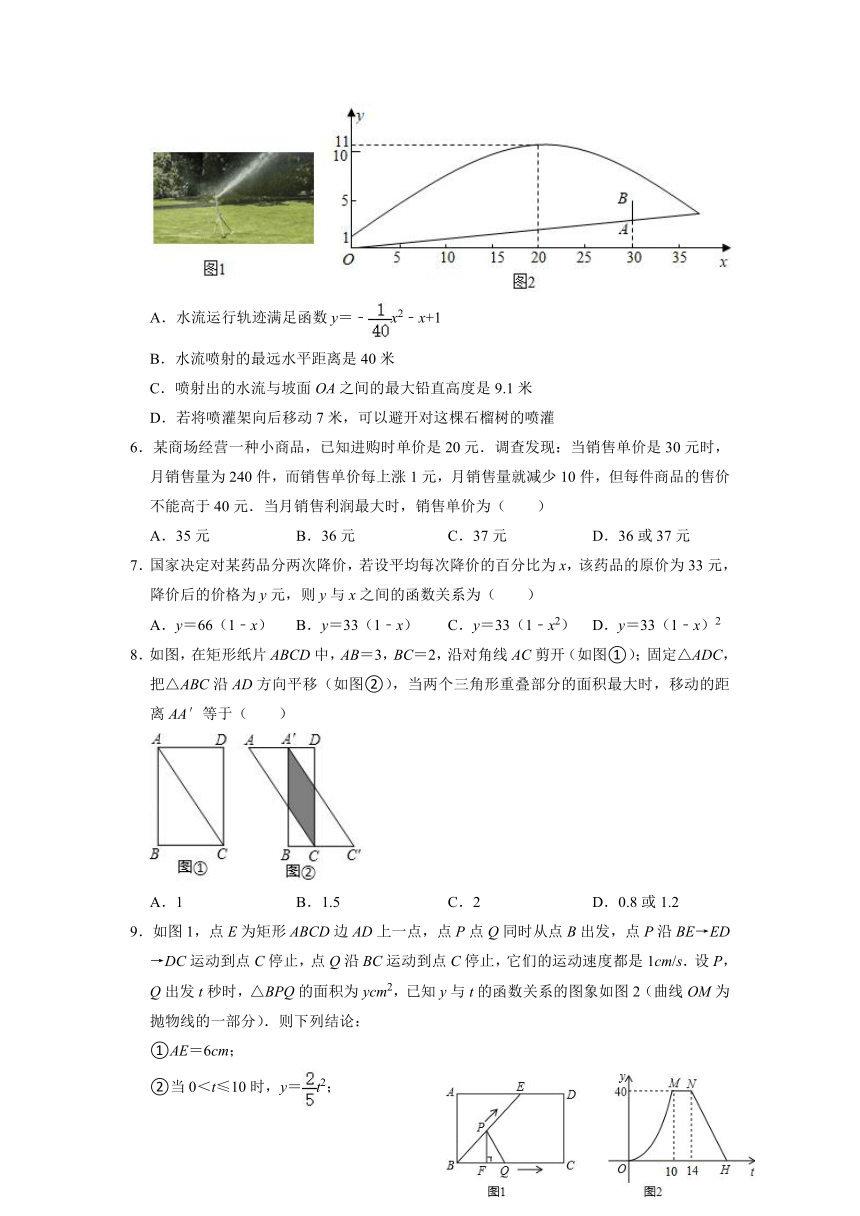
5.如图1,一个移动喷灌架喷射出的水流可以近似地看成抛物线.图2是喷灌架为一坡地草坪喷水的平面示意图,喷水头的高度(喷水头距喷灌架底部的距离)是1米.当喷射出的水流距离喷水头20米时,达到最大高度11米,现将喷灌架置于坡度为1:10的坡地底部点O处,草坡上距离O的水平距离为30米处有一棵高度约为2.3米的石榴树AB,因为刚刚被喷洒了农药,近期不能被喷灌.下列说法正确的是( )
A.水流运行轨迹满足函数y=﹣x2﹣x+1
B.水流喷射的最远水平距离是40米
C.喷射出的水流与坡面OA之间的最大铅直高度是9.1米
D.若将喷灌架向后移动7米,可以避开对这棵石榴树的喷灌
6.某商场经营一种小商品,已知进购时单价是20元.调查发现:当销售单价是30元时,月销售量为240件,而销售单价每上涨1元,月销售量就减少10件,但每件商品的售价不能高于40元.当月销售利润最大时,销售单价为( )
A.35元 B.36元 C.37元 D.36或37元
7.国家决定对某药品分两次降价,若设平均每次降价的百分比为x,该药品的原价为33元,降价后的价格为y元,则y与x之间的函数关系为( )
A.y=66(1﹣x) B.y=33(1﹣x) C.y=33(1﹣x2) D.y=33(1﹣x)2
8.如图,在矩形纸片ABCD中,AB=3,BC=2,沿对角线AC剪开(如图①);固定△ADC,把△ABC沿AD方向平移(如图②),当两个三角形重叠部分的面积最大时,移动的距离AA′等于( )
A.1 B.1.5 C.2 D.0.8或1.2
9.如图1,点E为矩形ABCD边AD上一点,点P点Q同时从点B出发,点P沿BE→ED→DC运动到点C停止,点Q沿BC运动到点C停止,它们的运动速度都是1cm/s.设P,Q出发t秒时,△BPQ的面积为ycm2,已知y与t的函数关系的图象如图2(曲线OM为抛物线的一部分).则下列结论:
①AE=6cm;
②当0<t≤10时,y=t2;
③直线NH的解析式为y=﹣5t+110;
④若△ABE与△QBP相似,则t=秒,
其中正确结论的个数为( )
A.1个 B.2个 C.3个 D.4个
二.填空题(共7小题,满分28分)
10.按照防疫要求,学生在进校时必须排队接受体温检测,某校统计了学生早晨到校情况,发现从7:00开始,在校门口的学生人数y随时间x(单位:分钟)的变化情况的图象是如图所示的某抛物线的一部分,则校门口排队等待体温检测的学生最多时有 人.
11.一名运动员在平地上推铅球,铅球出手时离地面的高度为米,出手后铅球离地面的高度y(米)与水平距离x(米)之间的函数关系式为,当铅球离地面的高度最大时,与出手点水平距离为5米,则该运动员推铅球的成绩为 米.
12.如图,一小球从斜坡O点处抛出,球的运行路线是抛物线y=4x﹣x2图象的一段,斜坡OA可以看成是一次函数y=x图象的一段.则小球在斜坡上的落点A的垂直高度为 .
13.如图,规格为60cm×60cm的正方形地砖在运输过程中受损,断去一角,量得AF=30cm,CE=45cm.现准备从五边形地砖ABCEF上截出一个面积为S的矩形地砖PMBN,则S最大值是 .
14.网络销售已经成为一种热门的销售方式,某网络平台为一服装厂直播代销一种服装(这里代销指厂家先免费提供货源,待货物销售后再进行结算,未售出的由厂家负责处理).销售中发现每件售价为250元时,日销售量为40件,当每件衣服每下降10元时,日销售量就会增加8件.已知每售出1件衣服,该平台需支付厂家和其它费用共100元.设每件衣服售价为x(元),该网络平台的日销售量为y(件).则下列结论正确的是 (填写所有正确结论序号).
①y与x的关系式是y=﹣x+240;
②y与x的关系式是y=x﹣160;
③设每天的利润为W元,则W与x的关系式是W=﹣+320x﹣24000;
④按照厂家规定,每件售价不得低于210元,若该经销商想要每天获得最大利润,当每件售价定为210元时,每天利润最大,此时最大利润为7920元.
15.某商场经营一种小商品,已知购进时单价是20元.调查发现:当销售单价是30元时,月销售量为280件.而销售单价每上涨1元,月销售量就减少10件,当月销售利润最大时,销售单价为 元.
16.某宾馆有50个房间供游客居住.当每个房间每天的定价为180元时,房间会全部住满;当每个房间每天的定价每增加10元时,就会有1个房间空闲.如果游客居住房间,宾馆需要对每个房间每天支出40元的各种费用.房价定为 元时,宾馆利润最大,最大利润是 元.
三.解答题(共8小题,满分65分)
17.甲、乙两汽车出租公司均有50辆汽车对外出租,下面是两公司经理的一段对话:
甲公司经理:如果我公司每辆汽车月租费3000元,那么50辆汽车可以全部租出,如果每辆汽车的月租费每增加50元,那么将少租出1辆汽车.另外,公司为每辆租出的汽车支付月维护费200元.
乙公司经理:我公司每辆汽车月租费3500元,无论是否租出汽车,公司均需一次性支付月维护费共计1850元.
说明:①汽车数量为整数;②月利润=月租车费﹣月维护费;③两公司月利润差=月利润较高公司的利润﹣月利润较低公司的利润.
在两公司租出的汽车数量相等的条件下,根据上述信息,解决下列问题:
(1)当每个公司租出的汽车为10辆时,甲公司的月利润是 元;
(2)当每个公司租出的汽车为 辆时,两公司的月利润相等;
(3)求两公司月利润差的最大值.
18.某网店经营一种热销的小商品,若该商品的售价为每件25元,第x天(x为正整数)的每件进价为y元,y与x的对应关系如下(为所学过的一次函数或二次函数中的一种):
第x天 1 2 3 4 …
每件进价(单位:元) 12 12.5 13 13.5 …
(1)直接写出y与x的函数关系式;
(2)统计发现该网店每天卖掉的件数m=4x+20,设该店每天的利润为w元;
①求该店每天利润的最大值;
②若该店每卖一件小商品就捐n元给某慈善组织(n>0),该店若想在第5天获得最大利润,求n的取值范围.
19.某商店经销一种销售成本为30元/kg的水产品,据市场分析:若按50元/kg销售,一个月能售出300kg,销售单价每涨1元,月销售量就减少10kg.设售价为x元/kg(x>50),月销售量为ykg;
(1)求月销售量y与售价x之间的函数解析式;
(2)当售价定为多少时,月销售利润最大?最大利润是多少?
(3)商店想在月销售成本不超过6000元的情况下,使得月销售利润不少于4000元,销售单价应定在什么范围?请直接写出售价x的取值范围.
20.如图,现有一块木板余料ABCED,它可以看作是缺了一个角的矩形,∠A=∠B=∠D=90°,AB=6dm,AD=10dm,BC=4dm,ED=2m,小天同学准备从这块余料中裁出一个矩形AFPQ(P为线段CE上一动点),设AF=xdm,矩形AFPQ的面积为ydm2.
(1)求y与x之间的函数关系式;
(2)小天认为矩形AFPQ的最大面积不会超过28dm2,请通过计算说明小天的想法是否正确?
21.某社区决定把一块长为50m、宽30m的矩形空地建为居民健身广场,设计方案如图所示,阴影区域为绿化区(四块绿化区均为大小、形状都相同的矩形),空白区域为活动区,且四周的四个出口宽度相同,其宽度不小于14m,不大于26m,设绿化区较长边为xm,活动区的面积为ym2.
(1)求y与x的函数表达式并求出自变量x的取值范围;
(2)求活动区最大面积.
22.鄂尔多斯旅游业的发展带动了当地的餐饮和住宿消费,某酒店房间实行淡、旺季两种价格标准收费,旺季每间的价格比淡季上涨.据统计,淡季时该酒店平均每天有10间房空余,每天总收入为4800元;旺季时所有房间能全部住满,每天总收入为8000元.
(1)该酒店共有房间多少间?淡季时每间房的日租金是多少元?
(2)经市场调查发现,旺季每个房间的价格每上涨10元,每天入住的房间就会减少1间,请写出每日房间的入住数y间与每个房间涨价x元的关系式;
(3)在(2)的条件下,不考虑其它因素,每个房间上涨多少元时,该酒店的日收入最高?最高收入是多少元?
23.某植物园有一块足够大的空地,其中有一堵长为6米的墙,现准备用20米的篱笆围两间矩形花圃,中间用篱笆隔开.小俊设计了如图所示的两种方案:
方案甲中AD的长不超过墙长;方案乙中AD的长大于墙长.
(1)若按方案甲施工,且围成面积为25平方米的花圃,则AD的长是多少米?
(2)按哪种方案施工,可以围成的矩形花圃的面积最大?最大面积是多少?
24.2020年一场突如其来的新冠病毒在全球蔓延,我国政府以人为本,领导全国人民打了一场卓越的抗疫阻击战,取得了阶段性的成果.在疫情期间,某市政府对销售防疫产品的商店进行补贴,该市规定销售某一消毒液销售价不高于45元/件可获政府补贴金5元/件,已知这种产品的成本价为30元/件.每天销售量y(件)与销售单价x(元/件)之间存在一次函数关系,如图所示.
(1)求这种产品每天的销售量(单位:件)与销售单价x(单位:元/件)之间的函数关系.
(2)这种产品销售单价定为多少元时,商店每天的销售利润既最大,又能获得政府补贴?商店共获利多少元?
参考答案
一.选择题(共9小题,满分27分)
1.解:建立平面直角坐标系,设横轴x通过AB,纵轴y通过AB中点O且通过C点,则通过画图可得知O为原点,
抛物线以y轴为对称轴,且经过A,B两点,可求出OA和OB为AB的一半2米,抛物线顶点C坐标为(0,2),
设顶点式y=ax2+2,代入A点坐标(﹣2,0),
得:a=﹣0.5,
所以抛物线解析式为y=﹣0.5x2+2,
把x=﹣3代入抛物线解析式得出:
y=﹣0.5×(﹣3)2+2=﹣2.5,
∴水面下降2.5米,
故选:C.
2.解:设每月总利润为w,依题意得w=y(x﹣50)=(﹣5x+550)(x﹣50)=﹣5x2+800x﹣27500=﹣5(x﹣80)2+4500,
∵﹣5<0,此图象开口向下,
∴当x=80时,w有最大值为4500元,
∴为了每月所获利润最大,该商品销售单价应定为80元.
故选:B.
3.解:∵每涨价1元,每星期要少卖出5件,每件涨价x元,
∴销售每件的利润为(40﹣20+x)元,每星期的销售量为(200﹣5x)件,
∴每星期售出商品的利润y=(200﹣5x)(40﹣20+x).
故选:A.
4.解:如图,建立直角坐标系,设抛物线解析式为y=a(x﹣6)2+3,
将(0,0)代入解析式得a=,
∴抛物线解析式为y=(x﹣6)2+3,
当x=10时,y=,<2.44,满足题意,
故选:A.
5.解:由题意可设抛物线的解析式为y=a(x﹣20)2+k,
将(0,1),(20,11)分别代入,得:,解得:,
∴y=﹣(x﹣20)2+11
=﹣x2+x+1,
故A错误;
∵坡度为1:10,
∴直线OA的解析式为y=0.1x,
当x=40时,y=0.1×40=4,
令y=4,得﹣x2+x+1=4,
∴x2﹣40x+120=0,
解得x=20±2≠40,
∴B错误;
设喷射出的水流与坡面OA之间的铅直高度为h米,
则h=﹣x2+x+1﹣0.1x=﹣x2+x+1,
∴对称轴为x=﹣=18,
∴hmax=9.1,故C正确;
将喷灌架向后移动7米,则图2中x=30时抛物线上的点的纵坐标值等于x=37时的函数值,
当x=37时,y=﹣×372+37+1=3.775,
在图2中,当x=30时,点B的纵坐标为:0.1×30+2.3=5.3,
则点A的纵坐标为5.3﹣2.3=3<3.775,故D错误.
故选:C.
6.解:设销售单价上涨x元,月销售利润为y元.
∵每件商品售价不能高于40元,
∴0≤x≤10,
依题意得:
y=(30﹣20+x)(240﹣10x)
=(10+x)(240﹣10x)
=﹣10x2+140x+2400
=﹣10(x﹣7)2+2890,
∴当x=7时,y最大=2890,
∴每件商品售价为30+7=37(元),
故选:C.
7.解:根据题意:平均每次降价的百分比为x,该药品的原价为33元,降价后的价格为y元,
可得y与x之间的函数关系为:y=33(1﹣x)2.
故选:D.
8.解:如图,设A′B交AC于点E,
tan∠DAC==,
设AA′=x,A′D=2﹣x,
∵AD=2,DC=3,
∴=,
∴A′E=x,
∵两个三角形重叠部分的面积是S=A′E×A′D=x(2﹣x)=﹣(x﹣1)2+,
当x=1时,阴影部分的面积最大,
AA′=1,
故选:A.
9.解:①观察图2可知:
当t=10时,点P、E重合,点Q、C重合;
当t=14时,点P、D重合.
∴BE=BC=10,DE=14﹣10=4,
∴AE=AD﹣DE=BC﹣DE=6,
∴①正确;
②设抛物线OM的函数解析式为y=ax2,
将点(10,40)代入y=ax2中,
得:40=100a,解得:a=,
∴当0<t≤10时,y=t2,②成立;
③在Rt△ABE中,∠BAE=90°,BE=10,AE=6,
∴AB==8,
∴点H的坐标为(14+8,0),即(22,0),
设直线NH的解析式为y=kt+b,
∴,解得:,
∴直线NH的解析式为y=﹣5t+110,③成立;
④当0<t≤10时,△QBP为等腰三角形,
△ABE为边长比为6:8:10的直角三角形,
∴当t=秒时,△ABE与△QBP不相似,④不正确.
综上可知:正确的结论有3个.
故选:C.
二.填空题(共7小题,满分28分)
10.解:设y与x之间的函数解析式为y=ax2+bx+c,
根据题意,得:,
解得:,
∴y=﹣x2+16x+34,
∵﹣<0,
∴y有最大值,y最大===162,
∴校门口排队等待体温检测的学生人数最多时有162人.
故答案为:162.
11.解:设铅球出手点为点A,根据题意建立平面直角坐标系,如图:
∵当铅球离地面的高度最大时,与出手点水平距离为5米,
∴抛物线的对称轴为直线x=5,
∴﹣=﹣==5,
则b=,
又∵抛物线经过(0,),
∴c=,
∴y=﹣x2+x+,
当x=0时,﹣x2+x+=0,
整理得:x2﹣10x﹣24=0,
解得:x1=﹣2(舍去),x2=12,
故答案安为:12.
12.解:由题意知,
﹣x2+4x=x,
解得:x=7,
把x=7代入抛物线y=﹣x2+4x中,
即y=﹣×72+4×7=﹣+28=,
小球在斜坡上的落点A的垂直高度为.
故答案为:.
13.解:延长MP交CD与点G,
则EG=y﹣45,PG=60﹣x.
∵PG∥FD,
∴△EPG∽△EFD,
∴y=﹣x+75(30≤x≤60),
∴S=xy=(﹣x+75)x=﹣x2+75x=﹣(x﹣75)2+,
∵﹣<0,
∴当x<75时,S随x的增大而增大,
∵30≤x≤60,
∴当x=60时,S最大,最大值为2700cm2.
故答案为:2700cm2.
14.解:∵y=40+=﹣x+240,
∴①正确,②错误;
∵w=(x﹣100)(﹣x+240)=﹣+320x﹣24000;
∴③正确;
∵w=(x﹣100)(﹣x+240)=﹣+320x﹣24000=﹣(x﹣200)2+8000,
a=﹣<0,每件售价不得低于210元,
所以当x=210时,每天利润最大是7920元,
∴④正确.
故答案为:①③④.
15.解:设销售单价为x元时,销售利润最大,
单价利润为(x﹣20)元,
销售数量为280﹣(x﹣30) 10,
∴利润总额为y=(x﹣20) [280﹣(x﹣30) 10],
化简得:y=﹣10x2+780x﹣11600,
配方得:y=﹣10(x﹣39)2+3160,
当单价为39元时,有最大利润3610元,
故答案为:39.
16.解:设空闲房间为x个,则定价增加了10x元,设宾馆的利润为y元,由题意得:
y=(180+10x﹣40)(50﹣x)
=﹣10x2+360x+7000
=﹣10(x﹣18)2+10240,
∵a=﹣10<0,抛物线开口向下,
∴当x=18时,y有最大值,为10240.
此时房间定价为180+10×18=360(元).
∴房间定价为360元时,利润最大,最大利润为10240元.
故答案为:360,10240.
三.解答题(共8小题,满分65分)
17.解:(1)[(50﹣10)×50+3000]×10﹣200×10=48000元,
当每个公司租出的汽车为10辆时,甲公司的月利润是48000元,
故答案为:48000;
(2)设每个公司租出的汽车为x辆,
由题意可得:[(50﹣x)×50+3000]x﹣200x=3500x﹣1850,
解得:x=37或x=﹣1(舍),
∴当每个公司租出的汽车为37辆时,两公司的月利润相等,
故答案为:37;
(3)设两公司的月利润分别为y甲,y乙,月利润差为y,
则y甲=[(50﹣x)×50+3000]x﹣200x,
y乙=3500x﹣1850,
当甲公司的利润大于乙公司时,0<x<37,
y=y甲﹣y乙=[(50﹣x)×50+3000]x﹣200x﹣(3500x﹣1850)
=﹣50x2+1800x+1850,
当x=﹣=18时,利润差最大,且为18050元;
当乙公司的利润大于甲公司时,37<x≤50,
y=y乙﹣y甲=3500x﹣1850﹣[(50﹣x)×50+3000]x+200x
=50x2﹣1800x﹣1850,
∵对称轴为直线x=﹣=18,50>0,
∴当37<x≤50时,y随x的增大而增大,
∴当x=50时,利润差最大,且为33150元,
综上:两公司月利润差的最大值为33150元.
18.解:(1)通过表中数据可知,y与x的函数关系为一次函数,
设y与x的函数关系式为y=kx+b,
把x=1,y=12和x=3,y=13代入y=kx+b得:
,
解得:,
∴y与x的函数关系式为y=x+;
(2)①根据题意,得:
w=25m﹣my
=(25﹣y) m
=(25﹣x﹣)(4x+20)
=﹣x2+44x+270
=﹣2(x﹣11)2+512,
∵﹣2<0,
∴当x=11时,w有最大值,最大值为512,
∴该店每天利润的最大值为512元;
②捐赠后的利润为w′=25m﹣my﹣nm
=﹣2x2+44x+270﹣4nx﹣20n,
第5天的利润为:440﹣40n,
第4天的利润为:414﹣36n,
第6天的利润为:462﹣44n,
要想在第5天利润最大,
则,
解得:,
∴n的取值范围为<n<.
19.解:(1)由题意可得,
y=300﹣(x﹣50)×10=﹣10x+800,
即月销售量y与售价x之间的函数解析式是y=﹣10x+800;
(2)设利润为w元,
由题意可得w=(x﹣30)(﹣10x+800)=﹣10(x﹣55)2+6250,
∴当x=55时,w取得最大值,此时w=6250,
答:当售价定为55元时,月销售利润最大,最大利润是6250元;
(3)∵月销售成本不超过6000元,月销售利润不少于4000元,
∴,
解得60≤x≤70,
即x的取值范围是60≤x≤70.
20.解:(1)分别延长DE,FP,与BC的延长线相交于G,H,
∵AF=x,
∴CH=x﹣4,
设AQ=z,PH=BQ=6﹣z,
∵PH∥EG,
∴=,即=,
化简得z=,
∴y= x=﹣x2+x (4≤x≤10);
(2)y=﹣x2+x=﹣(x﹣)2+,
当x=dm时,y取最大值,最大值是=28>28,
∵矩形AFPQ的最大面积超过28dm2.
∴小天的想法不正确.
21.解:(1)根据题意,绿化区的宽为:[30﹣(50﹣2x)]÷2=(x﹣10)m,
∴y=50×30﹣4x(x﹣10)=﹣4x2+40x+1500,
∵4个出口宽度相同,其宽度不小于14m,不大于26m,
即14≤50﹣2x≤26,
∴12≤x≤18,
∴y与x的函数表达式为y=﹣4x2+40x+1500(12≤x≤18);
(2)y=﹣4x2+40x+1500=﹣4(x﹣5)2+1600,
∵a=﹣4<0,抛物线的开口向下,
当x≥5时,y随x的增大而减小,
∵12≤x≤18,
∴当x=12时,y有最大值,最大值为1404,
答:活动区的最大面积为1404m2.
22.解:(1)设淡季每间的价格为a元,酒店房间有b间,
由题意,得:,
解得:,
答:该酒店有房间50间,淡季每间房的日租金是120元;
(2)设每个房间价格上涨x元,根据题意得,
y=50﹣=﹣x+50,
∴每日房间的入住数y间与每个房间涨价x元的关系式为y=﹣x+50;
(3)设该酒店的每日总收入为w元,由题意得:
w=(×120+x)(50﹣)=﹣x2+34x+8000=﹣(x﹣170)2+10890,
∵﹣<0,
∴当x=170时,y有最大值,最大值为10890,
∴每个房间上涨170元时,该酒店的日收入最高,最高收入是10890元.
23.解:(1)设AB的长是x米,则AD=20﹣3x,
根据题意得,x(20﹣3x)=25,
解得:x1=5,x2=,
当x=时,AD=15米>6米,
∴x=5,
∴AD=5米,
答:AD的长是5米;
(2)按甲方案:设BC的长是m米,矩形花圃的面积是y平方米,
则AB=(20﹣m)=(﹣m)米,
根据题意,得y=m(﹣m)=﹣(m﹣10)2+(0<m≤6),
∵﹣<0,
∴当m<10时,y随m的增大而增大,
∵0<m≤6,
当m=6时,y有最大值,最大值为28米.
按乙方案:设BC的长是n米,矩形花圃的最大面积是S平方米,则AB=[20﹣n﹣(n﹣6)]=(﹣n)米,
根据题意得,S=n(﹣n)=﹣(n﹣)2+(6<n<13),
∴当x=时,y有最大值为,
∵28<,
∴按图乙的方案施工,围成的矩形花圃的最大面积,最大面积是平方米.
24.解:(1)设y=kx+b,
∵图象过(40,20)与(50,10),
∴,
解得:,
∴y=﹣x+60;
(2)设销售利润为W元,
W=(x﹣30) y=(x﹣30)(﹣x+60)=﹣x2+90x﹣1800=﹣(x﹣45)2+225,
∵﹣1<0,
∴当x=45时,W有最大值,最大值为225,
∵45元没有高于45,
∴可以获补贴,
∴x=45时,y=15,
∴补贴总额:15×5=75(元),
∴共获利225+75=300(元).
∴这种产品销售单价定为45元时,商店每天的销售利润既最大,又能获得政府补贴,商店共获利300元.
一.选择题(共9小题,满分27分)
1.如图是抛物线形的拱桥,当水面宽4m时,顶点离水面2m,当水面宽度增加到6m时,水面下降( )
A.1m B.1.5m C.2.5m D.2m
2.某超市销售一种商品,每件成本为50元,销售人员经调查发现,该商品每月的销售量y(件)与销售单价x(元)之间满足函数关系式y=﹣5x+550,若要求销售单价不得低于成本,为了每月所获利润最大,该商品销售单价应定为多少元?每月最大利润是多少?( )
A.90元,4500元 B.80元,4500元
C.90元,4000元 D.80元,4000元
3.某商品的进价为每件20元,现在的售价为每件40元,每星期可卖出200件.市场调查反映:如调整价格,每涨价1元,每星期要少卖出5件.则每星期售出商品的利润y(单位:元)与每件涨价x(单位:元)之间的函数关系式是( )
A.y=(200﹣5x)(40﹣20+x) B.y=(200+5x)(40﹣20﹣x)
C.y=200(40﹣20﹣x) D.y=200﹣5x
4.一次足球训练中,小明从球门正前方将球射向球门,球射向球门的路线呈抛物线.当球飞行的水平距离为6m时,球达到最高点,此时球离地面3m.已知球门高是2.44m,若足球能射入球门,则小明与球门的距离可能是( )
A.10m B.8m C.6m D.5m
5.如图1,一个移动喷灌架喷射出的水流可以近似地看成抛物线.图2是喷灌架为一坡地草坪喷水的平面示意图,喷水头的高度(喷水头距喷灌架底部的距离)是1米.当喷射出的水流距离喷水头20米时,达到最大高度11米,现将喷灌架置于坡度为1:10的坡地底部点O处,草坡上距离O的水平距离为30米处有一棵高度约为2.3米的石榴树AB,因为刚刚被喷洒了农药,近期不能被喷灌.下列说法正确的是( )
A.水流运行轨迹满足函数y=﹣x2﹣x+1
B.水流喷射的最远水平距离是40米
C.喷射出的水流与坡面OA之间的最大铅直高度是9.1米
D.若将喷灌架向后移动7米,可以避开对这棵石榴树的喷灌
6.某商场经营一种小商品,已知进购时单价是20元.调查发现:当销售单价是30元时,月销售量为240件,而销售单价每上涨1元,月销售量就减少10件,但每件商品的售价不能高于40元.当月销售利润最大时,销售单价为( )
A.35元 B.36元 C.37元 D.36或37元
7.国家决定对某药品分两次降价,若设平均每次降价的百分比为x,该药品的原价为33元,降价后的价格为y元,则y与x之间的函数关系为( )
A.y=66(1﹣x) B.y=33(1﹣x) C.y=33(1﹣x2) D.y=33(1﹣x)2
8.如图,在矩形纸片ABCD中,AB=3,BC=2,沿对角线AC剪开(如图①);固定△ADC,把△ABC沿AD方向平移(如图②),当两个三角形重叠部分的面积最大时,移动的距离AA′等于( )
A.1 B.1.5 C.2 D.0.8或1.2
9.如图1,点E为矩形ABCD边AD上一点,点P点Q同时从点B出发,点P沿BE→ED→DC运动到点C停止,点Q沿BC运动到点C停止,它们的运动速度都是1cm/s.设P,Q出发t秒时,△BPQ的面积为ycm2,已知y与t的函数关系的图象如图2(曲线OM为抛物线的一部分).则下列结论:
①AE=6cm;
②当0<t≤10时,y=t2;
③直线NH的解析式为y=﹣5t+110;
④若△ABE与△QBP相似,则t=秒,
其中正确结论的个数为( )
A.1个 B.2个 C.3个 D.4个
二.填空题(共7小题,满分28分)
10.按照防疫要求,学生在进校时必须排队接受体温检测,某校统计了学生早晨到校情况,发现从7:00开始,在校门口的学生人数y随时间x(单位:分钟)的变化情况的图象是如图所示的某抛物线的一部分,则校门口排队等待体温检测的学生最多时有 人.
11.一名运动员在平地上推铅球,铅球出手时离地面的高度为米,出手后铅球离地面的高度y(米)与水平距离x(米)之间的函数关系式为,当铅球离地面的高度最大时,与出手点水平距离为5米,则该运动员推铅球的成绩为 米.
12.如图,一小球从斜坡O点处抛出,球的运行路线是抛物线y=4x﹣x2图象的一段,斜坡OA可以看成是一次函数y=x图象的一段.则小球在斜坡上的落点A的垂直高度为 .
13.如图,规格为60cm×60cm的正方形地砖在运输过程中受损,断去一角,量得AF=30cm,CE=45cm.现准备从五边形地砖ABCEF上截出一个面积为S的矩形地砖PMBN,则S最大值是 .
14.网络销售已经成为一种热门的销售方式,某网络平台为一服装厂直播代销一种服装(这里代销指厂家先免费提供货源,待货物销售后再进行结算,未售出的由厂家负责处理).销售中发现每件售价为250元时,日销售量为40件,当每件衣服每下降10元时,日销售量就会增加8件.已知每售出1件衣服,该平台需支付厂家和其它费用共100元.设每件衣服售价为x(元),该网络平台的日销售量为y(件).则下列结论正确的是 (填写所有正确结论序号).
①y与x的关系式是y=﹣x+240;
②y与x的关系式是y=x﹣160;
③设每天的利润为W元,则W与x的关系式是W=﹣+320x﹣24000;
④按照厂家规定,每件售价不得低于210元,若该经销商想要每天获得最大利润,当每件售价定为210元时,每天利润最大,此时最大利润为7920元.
15.某商场经营一种小商品,已知购进时单价是20元.调查发现:当销售单价是30元时,月销售量为280件.而销售单价每上涨1元,月销售量就减少10件,当月销售利润最大时,销售单价为 元.
16.某宾馆有50个房间供游客居住.当每个房间每天的定价为180元时,房间会全部住满;当每个房间每天的定价每增加10元时,就会有1个房间空闲.如果游客居住房间,宾馆需要对每个房间每天支出40元的各种费用.房价定为 元时,宾馆利润最大,最大利润是 元.
三.解答题(共8小题,满分65分)
17.甲、乙两汽车出租公司均有50辆汽车对外出租,下面是两公司经理的一段对话:
甲公司经理:如果我公司每辆汽车月租费3000元,那么50辆汽车可以全部租出,如果每辆汽车的月租费每增加50元,那么将少租出1辆汽车.另外,公司为每辆租出的汽车支付月维护费200元.
乙公司经理:我公司每辆汽车月租费3500元,无论是否租出汽车,公司均需一次性支付月维护费共计1850元.
说明:①汽车数量为整数;②月利润=月租车费﹣月维护费;③两公司月利润差=月利润较高公司的利润﹣月利润较低公司的利润.
在两公司租出的汽车数量相等的条件下,根据上述信息,解决下列问题:
(1)当每个公司租出的汽车为10辆时,甲公司的月利润是 元;
(2)当每个公司租出的汽车为 辆时,两公司的月利润相等;
(3)求两公司月利润差的最大值.
18.某网店经营一种热销的小商品,若该商品的售价为每件25元,第x天(x为正整数)的每件进价为y元,y与x的对应关系如下(为所学过的一次函数或二次函数中的一种):
第x天 1 2 3 4 …
每件进价(单位:元) 12 12.5 13 13.5 …
(1)直接写出y与x的函数关系式;
(2)统计发现该网店每天卖掉的件数m=4x+20,设该店每天的利润为w元;
①求该店每天利润的最大值;
②若该店每卖一件小商品就捐n元给某慈善组织(n>0),该店若想在第5天获得最大利润,求n的取值范围.
19.某商店经销一种销售成本为30元/kg的水产品,据市场分析:若按50元/kg销售,一个月能售出300kg,销售单价每涨1元,月销售量就减少10kg.设售价为x元/kg(x>50),月销售量为ykg;
(1)求月销售量y与售价x之间的函数解析式;
(2)当售价定为多少时,月销售利润最大?最大利润是多少?
(3)商店想在月销售成本不超过6000元的情况下,使得月销售利润不少于4000元,销售单价应定在什么范围?请直接写出售价x的取值范围.
20.如图,现有一块木板余料ABCED,它可以看作是缺了一个角的矩形,∠A=∠B=∠D=90°,AB=6dm,AD=10dm,BC=4dm,ED=2m,小天同学准备从这块余料中裁出一个矩形AFPQ(P为线段CE上一动点),设AF=xdm,矩形AFPQ的面积为ydm2.
(1)求y与x之间的函数关系式;
(2)小天认为矩形AFPQ的最大面积不会超过28dm2,请通过计算说明小天的想法是否正确?
21.某社区决定把一块长为50m、宽30m的矩形空地建为居民健身广场,设计方案如图所示,阴影区域为绿化区(四块绿化区均为大小、形状都相同的矩形),空白区域为活动区,且四周的四个出口宽度相同,其宽度不小于14m,不大于26m,设绿化区较长边为xm,活动区的面积为ym2.
(1)求y与x的函数表达式并求出自变量x的取值范围;
(2)求活动区最大面积.
22.鄂尔多斯旅游业的发展带动了当地的餐饮和住宿消费,某酒店房间实行淡、旺季两种价格标准收费,旺季每间的价格比淡季上涨.据统计,淡季时该酒店平均每天有10间房空余,每天总收入为4800元;旺季时所有房间能全部住满,每天总收入为8000元.
(1)该酒店共有房间多少间?淡季时每间房的日租金是多少元?
(2)经市场调查发现,旺季每个房间的价格每上涨10元,每天入住的房间就会减少1间,请写出每日房间的入住数y间与每个房间涨价x元的关系式;
(3)在(2)的条件下,不考虑其它因素,每个房间上涨多少元时,该酒店的日收入最高?最高收入是多少元?
23.某植物园有一块足够大的空地,其中有一堵长为6米的墙,现准备用20米的篱笆围两间矩形花圃,中间用篱笆隔开.小俊设计了如图所示的两种方案:
方案甲中AD的长不超过墙长;方案乙中AD的长大于墙长.
(1)若按方案甲施工,且围成面积为25平方米的花圃,则AD的长是多少米?
(2)按哪种方案施工,可以围成的矩形花圃的面积最大?最大面积是多少?
24.2020年一场突如其来的新冠病毒在全球蔓延,我国政府以人为本,领导全国人民打了一场卓越的抗疫阻击战,取得了阶段性的成果.在疫情期间,某市政府对销售防疫产品的商店进行补贴,该市规定销售某一消毒液销售价不高于45元/件可获政府补贴金5元/件,已知这种产品的成本价为30元/件.每天销售量y(件)与销售单价x(元/件)之间存在一次函数关系,如图所示.
(1)求这种产品每天的销售量(单位:件)与销售单价x(单位:元/件)之间的函数关系.
(2)这种产品销售单价定为多少元时,商店每天的销售利润既最大,又能获得政府补贴?商店共获利多少元?
参考答案
一.选择题(共9小题,满分27分)
1.解:建立平面直角坐标系,设横轴x通过AB,纵轴y通过AB中点O且通过C点,则通过画图可得知O为原点,
抛物线以y轴为对称轴,且经过A,B两点,可求出OA和OB为AB的一半2米,抛物线顶点C坐标为(0,2),
设顶点式y=ax2+2,代入A点坐标(﹣2,0),
得:a=﹣0.5,
所以抛物线解析式为y=﹣0.5x2+2,
把x=﹣3代入抛物线解析式得出:
y=﹣0.5×(﹣3)2+2=﹣2.5,
∴水面下降2.5米,
故选:C.
2.解:设每月总利润为w,依题意得w=y(x﹣50)=(﹣5x+550)(x﹣50)=﹣5x2+800x﹣27500=﹣5(x﹣80)2+4500,
∵﹣5<0,此图象开口向下,
∴当x=80时,w有最大值为4500元,
∴为了每月所获利润最大,该商品销售单价应定为80元.
故选:B.
3.解:∵每涨价1元,每星期要少卖出5件,每件涨价x元,
∴销售每件的利润为(40﹣20+x)元,每星期的销售量为(200﹣5x)件,
∴每星期售出商品的利润y=(200﹣5x)(40﹣20+x).
故选:A.
4.解:如图,建立直角坐标系,设抛物线解析式为y=a(x﹣6)2+3,
将(0,0)代入解析式得a=,
∴抛物线解析式为y=(x﹣6)2+3,
当x=10时,y=,<2.44,满足题意,
故选:A.
5.解:由题意可设抛物线的解析式为y=a(x﹣20)2+k,
将(0,1),(20,11)分别代入,得:,解得:,
∴y=﹣(x﹣20)2+11
=﹣x2+x+1,
故A错误;
∵坡度为1:10,
∴直线OA的解析式为y=0.1x,
当x=40时,y=0.1×40=4,
令y=4,得﹣x2+x+1=4,
∴x2﹣40x+120=0,
解得x=20±2≠40,
∴B错误;
设喷射出的水流与坡面OA之间的铅直高度为h米,
则h=﹣x2+x+1﹣0.1x=﹣x2+x+1,
∴对称轴为x=﹣=18,
∴hmax=9.1,故C正确;
将喷灌架向后移动7米,则图2中x=30时抛物线上的点的纵坐标值等于x=37时的函数值,
当x=37时,y=﹣×372+37+1=3.775,
在图2中,当x=30时,点B的纵坐标为:0.1×30+2.3=5.3,
则点A的纵坐标为5.3﹣2.3=3<3.775,故D错误.
故选:C.
6.解:设销售单价上涨x元,月销售利润为y元.
∵每件商品售价不能高于40元,
∴0≤x≤10,
依题意得:
y=(30﹣20+x)(240﹣10x)
=(10+x)(240﹣10x)
=﹣10x2+140x+2400
=﹣10(x﹣7)2+2890,
∴当x=7时,y最大=2890,
∴每件商品售价为30+7=37(元),
故选:C.
7.解:根据题意:平均每次降价的百分比为x,该药品的原价为33元,降价后的价格为y元,
可得y与x之间的函数关系为:y=33(1﹣x)2.
故选:D.
8.解:如图,设A′B交AC于点E,
tan∠DAC==,
设AA′=x,A′D=2﹣x,
∵AD=2,DC=3,
∴=,
∴A′E=x,
∵两个三角形重叠部分的面积是S=A′E×A′D=x(2﹣x)=﹣(x﹣1)2+,
当x=1时,阴影部分的面积最大,
AA′=1,
故选:A.
9.解:①观察图2可知:
当t=10时,点P、E重合,点Q、C重合;
当t=14时,点P、D重合.
∴BE=BC=10,DE=14﹣10=4,
∴AE=AD﹣DE=BC﹣DE=6,
∴①正确;
②设抛物线OM的函数解析式为y=ax2,
将点(10,40)代入y=ax2中,
得:40=100a,解得:a=,
∴当0<t≤10时,y=t2,②成立;
③在Rt△ABE中,∠BAE=90°,BE=10,AE=6,
∴AB==8,
∴点H的坐标为(14+8,0),即(22,0),
设直线NH的解析式为y=kt+b,
∴,解得:,
∴直线NH的解析式为y=﹣5t+110,③成立;
④当0<t≤10时,△QBP为等腰三角形,
△ABE为边长比为6:8:10的直角三角形,
∴当t=秒时,△ABE与△QBP不相似,④不正确.
综上可知:正确的结论有3个.
故选:C.
二.填空题(共7小题,满分28分)
10.解:设y与x之间的函数解析式为y=ax2+bx+c,
根据题意,得:,
解得:,
∴y=﹣x2+16x+34,
∵﹣<0,
∴y有最大值,y最大===162,
∴校门口排队等待体温检测的学生人数最多时有162人.
故答案为:162.
11.解:设铅球出手点为点A,根据题意建立平面直角坐标系,如图:
∵当铅球离地面的高度最大时,与出手点水平距离为5米,
∴抛物线的对称轴为直线x=5,
∴﹣=﹣==5,
则b=,
又∵抛物线经过(0,),
∴c=,
∴y=﹣x2+x+,
当x=0时,﹣x2+x+=0,
整理得:x2﹣10x﹣24=0,
解得:x1=﹣2(舍去),x2=12,
故答案安为:12.
12.解:由题意知,
﹣x2+4x=x,
解得:x=7,
把x=7代入抛物线y=﹣x2+4x中,
即y=﹣×72+4×7=﹣+28=,
小球在斜坡上的落点A的垂直高度为.
故答案为:.
13.解:延长MP交CD与点G,
则EG=y﹣45,PG=60﹣x.
∵PG∥FD,
∴△EPG∽△EFD,
∴y=﹣x+75(30≤x≤60),
∴S=xy=(﹣x+75)x=﹣x2+75x=﹣(x﹣75)2+,
∵﹣<0,
∴当x<75时,S随x的增大而增大,
∵30≤x≤60,
∴当x=60时,S最大,最大值为2700cm2.
故答案为:2700cm2.
14.解:∵y=40+=﹣x+240,
∴①正确,②错误;
∵w=(x﹣100)(﹣x+240)=﹣+320x﹣24000;
∴③正确;
∵w=(x﹣100)(﹣x+240)=﹣+320x﹣24000=﹣(x﹣200)2+8000,
a=﹣<0,每件售价不得低于210元,
所以当x=210时,每天利润最大是7920元,
∴④正确.
故答案为:①③④.
15.解:设销售单价为x元时,销售利润最大,
单价利润为(x﹣20)元,
销售数量为280﹣(x﹣30) 10,
∴利润总额为y=(x﹣20) [280﹣(x﹣30) 10],
化简得:y=﹣10x2+780x﹣11600,
配方得:y=﹣10(x﹣39)2+3160,
当单价为39元时,有最大利润3610元,
故答案为:39.
16.解:设空闲房间为x个,则定价增加了10x元,设宾馆的利润为y元,由题意得:
y=(180+10x﹣40)(50﹣x)
=﹣10x2+360x+7000
=﹣10(x﹣18)2+10240,
∵a=﹣10<0,抛物线开口向下,
∴当x=18时,y有最大值,为10240.
此时房间定价为180+10×18=360(元).
∴房间定价为360元时,利润最大,最大利润为10240元.
故答案为:360,10240.
三.解答题(共8小题,满分65分)
17.解:(1)[(50﹣10)×50+3000]×10﹣200×10=48000元,
当每个公司租出的汽车为10辆时,甲公司的月利润是48000元,
故答案为:48000;
(2)设每个公司租出的汽车为x辆,
由题意可得:[(50﹣x)×50+3000]x﹣200x=3500x﹣1850,
解得:x=37或x=﹣1(舍),
∴当每个公司租出的汽车为37辆时,两公司的月利润相等,
故答案为:37;
(3)设两公司的月利润分别为y甲,y乙,月利润差为y,
则y甲=[(50﹣x)×50+3000]x﹣200x,
y乙=3500x﹣1850,
当甲公司的利润大于乙公司时,0<x<37,
y=y甲﹣y乙=[(50﹣x)×50+3000]x﹣200x﹣(3500x﹣1850)
=﹣50x2+1800x+1850,
当x=﹣=18时,利润差最大,且为18050元;
当乙公司的利润大于甲公司时,37<x≤50,
y=y乙﹣y甲=3500x﹣1850﹣[(50﹣x)×50+3000]x+200x
=50x2﹣1800x﹣1850,
∵对称轴为直线x=﹣=18,50>0,
∴当37<x≤50时,y随x的增大而增大,
∴当x=50时,利润差最大,且为33150元,
综上:两公司月利润差的最大值为33150元.
18.解:(1)通过表中数据可知,y与x的函数关系为一次函数,
设y与x的函数关系式为y=kx+b,
把x=1,y=12和x=3,y=13代入y=kx+b得:
,
解得:,
∴y与x的函数关系式为y=x+;
(2)①根据题意,得:
w=25m﹣my
=(25﹣y) m
=(25﹣x﹣)(4x+20)
=﹣x2+44x+270
=﹣2(x﹣11)2+512,
∵﹣2<0,
∴当x=11时,w有最大值,最大值为512,
∴该店每天利润的最大值为512元;
②捐赠后的利润为w′=25m﹣my﹣nm
=﹣2x2+44x+270﹣4nx﹣20n,
第5天的利润为:440﹣40n,
第4天的利润为:414﹣36n,
第6天的利润为:462﹣44n,
要想在第5天利润最大,
则,
解得:,
∴n的取值范围为<n<.
19.解:(1)由题意可得,
y=300﹣(x﹣50)×10=﹣10x+800,
即月销售量y与售价x之间的函数解析式是y=﹣10x+800;
(2)设利润为w元,
由题意可得w=(x﹣30)(﹣10x+800)=﹣10(x﹣55)2+6250,
∴当x=55时,w取得最大值,此时w=6250,
答:当售价定为55元时,月销售利润最大,最大利润是6250元;
(3)∵月销售成本不超过6000元,月销售利润不少于4000元,
∴,
解得60≤x≤70,
即x的取值范围是60≤x≤70.
20.解:(1)分别延长DE,FP,与BC的延长线相交于G,H,
∵AF=x,
∴CH=x﹣4,
设AQ=z,PH=BQ=6﹣z,
∵PH∥EG,
∴=,即=,
化简得z=,
∴y= x=﹣x2+x (4≤x≤10);
(2)y=﹣x2+x=﹣(x﹣)2+,
当x=dm时,y取最大值,最大值是=28>28,
∵矩形AFPQ的最大面积超过28dm2.
∴小天的想法不正确.
21.解:(1)根据题意,绿化区的宽为:[30﹣(50﹣2x)]÷2=(x﹣10)m,
∴y=50×30﹣4x(x﹣10)=﹣4x2+40x+1500,
∵4个出口宽度相同,其宽度不小于14m,不大于26m,
即14≤50﹣2x≤26,
∴12≤x≤18,
∴y与x的函数表达式为y=﹣4x2+40x+1500(12≤x≤18);
(2)y=﹣4x2+40x+1500=﹣4(x﹣5)2+1600,
∵a=﹣4<0,抛物线的开口向下,
当x≥5时,y随x的增大而减小,
∵12≤x≤18,
∴当x=12时,y有最大值,最大值为1404,
答:活动区的最大面积为1404m2.
22.解:(1)设淡季每间的价格为a元,酒店房间有b间,
由题意,得:,
解得:,
答:该酒店有房间50间,淡季每间房的日租金是120元;
(2)设每个房间价格上涨x元,根据题意得,
y=50﹣=﹣x+50,
∴每日房间的入住数y间与每个房间涨价x元的关系式为y=﹣x+50;
(3)设该酒店的每日总收入为w元,由题意得:
w=(×120+x)(50﹣)=﹣x2+34x+8000=﹣(x﹣170)2+10890,
∵﹣<0,
∴当x=170时,y有最大值,最大值为10890,
∴每个房间上涨170元时,该酒店的日收入最高,最高收入是10890元.
23.解:(1)设AB的长是x米,则AD=20﹣3x,
根据题意得,x(20﹣3x)=25,
解得:x1=5,x2=,
当x=时,AD=15米>6米,
∴x=5,
∴AD=5米,
答:AD的长是5米;
(2)按甲方案:设BC的长是m米,矩形花圃的面积是y平方米,
则AB=(20﹣m)=(﹣m)米,
根据题意,得y=m(﹣m)=﹣(m﹣10)2+(0<m≤6),
∵﹣<0,
∴当m<10时,y随m的增大而增大,
∵0<m≤6,
当m=6时,y有最大值,最大值为28米.
按乙方案:设BC的长是n米,矩形花圃的最大面积是S平方米,则AB=[20﹣n﹣(n﹣6)]=(﹣n)米,
根据题意得,S=n(﹣n)=﹣(n﹣)2+(6<n<13),
∴当x=时,y有最大值为,
∵28<,
∴按图乙的方案施工,围成的矩形花圃的最大面积,最大面积是平方米.
24.解:(1)设y=kx+b,
∵图象过(40,20)与(50,10),
∴,
解得:,
∴y=﹣x+60;
(2)设销售利润为W元,
W=(x﹣30) y=(x﹣30)(﹣x+60)=﹣x2+90x﹣1800=﹣(x﹣45)2+225,
∵﹣1<0,
∴当x=45时,W有最大值,最大值为225,
∵45元没有高于45,
∴可以获补贴,
∴x=45时,y=15,
∴补贴总额:15×5=75(元),
∴共获利225+75=300(元).
∴这种产品销售单价定为45元时,商店每天的销售利润既最大,又能获得政府补贴,商店共获利300元.
