3.8圆内接正多边形 同步达标训练 2021-2022学年北师大版九年级数学下册(word版含答案)
文档属性
| 名称 | 3.8圆内接正多边形 同步达标训练 2021-2022学年北师大版九年级数学下册(word版含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 464.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-05 21:24:52 | ||
图片预览

文档简介
2021-2022学年北师大版九年级数学下册《3.8圆内接正多边形》同步达标训练(附答案)
1.一个适当大的正六边形,它的一个顶点与一个边长为定值的小正六边形ABCDEF的中心O重合,且与边AB、CD相交于G、H(如图).图中阴影部分的面积记为S,三条线段GB、BC、CH的长度之和记为l,在大正六边形绕点O旋转过程中,下列说法正确的是( )
A.S变化,l不变 B.S不变,l变化
C.S变化,l变化 D.S与l均不变
2.如图,一个正六边形的一边长与它的一边相外切的圆的周长相等,当这个圆按箭头方向从某一位置沿正六边形的六边滚动,直至回到原出发位置时,则这个圆共转了( )
A.6圈 B.7圈 C.8圈 D.9圈
3.如图,已知正五边形ABCDE中,点F是BC的中点,P是线段EF上的动点,连接AP,BP,当AP+BP的值最小时,∠BPF的度数为( )
A.36° B.45° C.54° D.60°
4.如图,⊙O是正六边形ABCDEF的外接圆,点P在⊙O上(P不与A,B重合),则∠APB的度数为( )
A.30°或150° B.60°或120° C.30° D.60°
5.如图,正方形ABCD内接于⊙O.点E为上一点,连接BE、CE,若∠CBE=15°,BE=3,则BC的长为( )
A. B. C. D.
6.如图,在圆内接正六边形ABCDEF中,BF,BD分别交AC于点G,H.若该圆的半径为15cm,则线段GH的长为( )
A.cm B.5cm C.3cm D.10cm
7.如图,以正六边形ABCDEF的对角线BD为边,向右作等边三角形BDG,若四边形BCDG的面积为4,则五边形ABDEF的面积为( )
A.6 B.8 C.10 D.12
8.如图,等边三角形ABC和正方形ADEF都内接于⊙O,则AD:AB=( )
A.2: B.: C.: D.:2
9.如图,点O为正六边形的中心,P,Q分别从点A(1,0)同时出发,沿正六边形按图示方向运动,点P的速度为每秒1个单位长度,点Q的速度为每秒2个单位长度,则第2020次相遇地点的坐标为( )
A. B.(1,0) C. D.(﹣1,0)
10.已知正方形MNKO和正六边形ABCDEF边长均为1,把正方形放在正六边形外边,使OK边与AB边重合,如图所示,按下列步骤操作:将正方形在正六边形外绕点B顺时针旋转,使KN边与BC边重合,完成第一次旋转;再绕点C顺时针旋转,使NM边与CD边重合,完成第二次旋转;………在这样连续6次旋转的过程中,点M在图中直角坐标系中的纵坐标可能是( )
A. B.﹣2.2 C.2.3 D.﹣2.3
11.如图,边长为a的正六边形内有斜边为a、锐角为60°两个直角三角形,则= .
12.如图,点O为正六边形ABCDEF的中心,连接AC,若正六边形的边长为2,则点O到AC的距离OG的长为 .
13.如图,AD是正五边形ABCDE的一条对角线,以C为圆心,CB为半径画弧交AD于点F,连接CF,则∠CFD= °.
14.如图,正方形ABCD内接于⊙O,其边长为4,则⊙O的内接正三角形EFG的边长为 .
15.如图,正六边形ABCDEF的边长为4,两顶点A,B分别在x轴和y轴上运动,则顶点D到原点O的距离的最大值为 ;最小值为 .
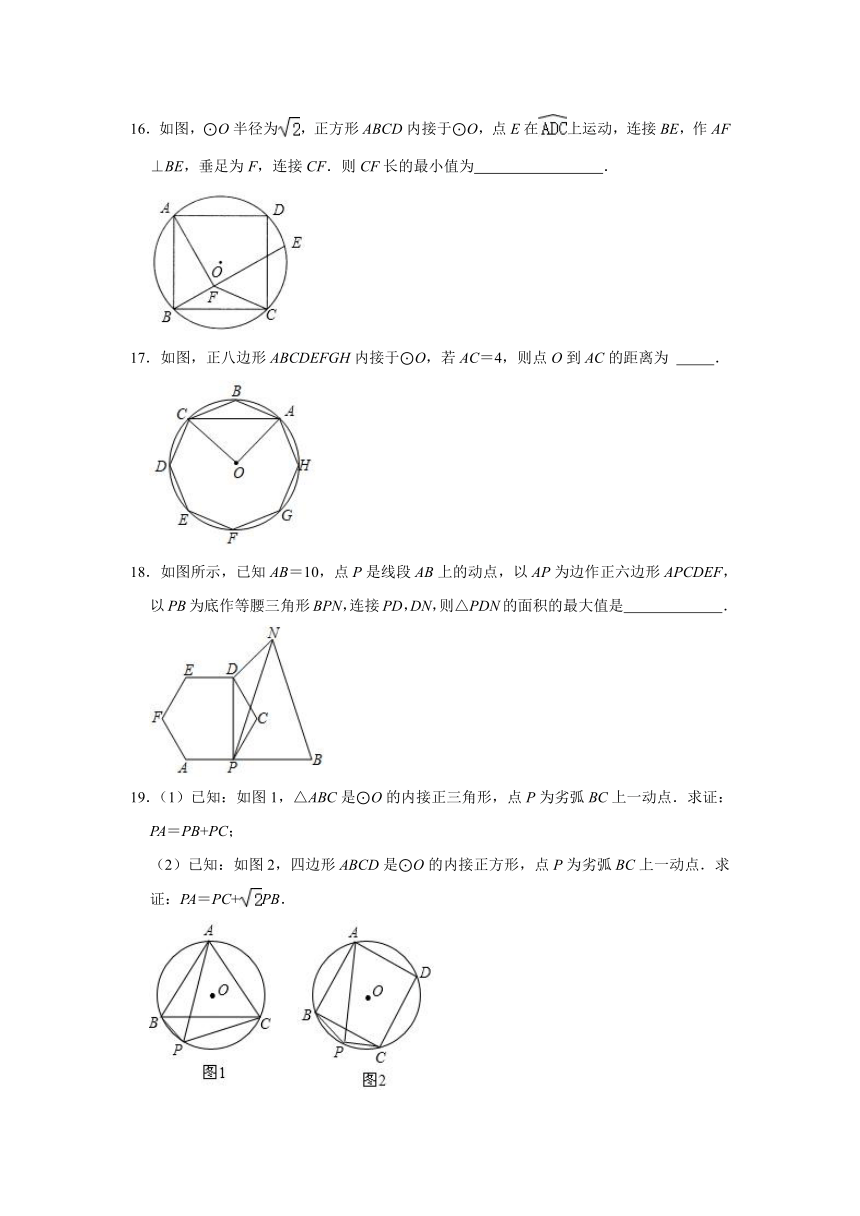
16.如图,⊙O半径为,正方形ABCD内接于⊙O,点E在上运动,连接BE,作AF⊥BE,垂足为F,连接CF.则CF长的最小值为 .
17.如图,正八边形ABCDEFGH内接于⊙O,若AC=4,则点O到AC的距离为 .
18.如图所示,已知AB=10,点P是线段AB上的动点,以AP为边作正六边形APCDEF,以PB为底作等腰三角形BPN,连接PD,DN,则△PDN的面积的最大值是 .
19.(1)已知:如图1,△ABC是⊙O的内接正三角形,点P为劣弧BC上一动点.求证:PA=PB+PC;
(2)已知:如图2,四边形ABCD是⊙O的内接正方形,点P为劣弧BC上一动点.求证:PA=PC+PB.
20.(1)已知:如图1,△ABC是⊙O的内接正三角形,点P为弧BC上一动点,求证:PA=PB+PC;
(2)如图2,四边形ABCD是⊙O的内接正方形,点P为弧BC上一动点,求证:;
(3)如图3,六边形ABCDEF是⊙O的内接正六边形,点P为弧BC上一动点,请探究PA、PB、PC三者之间有何数量关系,并给予证明.
参考答案
1.解:如图,连接OA,OC.
∵∠HOB=∠AOC=120°,∠OCH=∠OAG=60°,
∴∠HOC=∠GOA,
在△OHC和△OGA中,
,
∴△HOC≌△GOA(ASA),
∴AG=CH,
∴S阴=S四边形OABC=定值,l=GB+BC+CH=AG+BG+BC=2BC=定值,
故选:D.
2.解:如图所示:
由切线的性质得:圆从一边旋转到另一边时,圆心要绕六边形的顶点旋转60°,
则圆绕6个顶点一共旋转了360°,即转了1圈,
∵正六边形的一边长与它的一边相外切的圆的周长相等,
∴圆在正六边形的6条边上滚动时要转6圈,
∴这个圆共转了7圈,
故选:B.
3.解:如图,连接AC,PC,设AC交EF于点P′,连接BP′.
∵正五边形ABCDE中,点F是BC的中点,
∵EF⊥BC,
∴B,C关于EF对称,
∴PB=PB,
∵PA+PB=PA+PC≥AC,
∴当点P与P′重合时,PA+PB的值最小,
∵ABCDE是正五边形,
∴BA=BC,∠ABC=108°,
∴∠BAC=∠BCA=36°,
∵P′B=CP′,
∴∠P′BC=∠P′CB=36°,
∵∠EFB=90°,
∴∠BP′F=90°﹣36°=54°.
故选:C.
4.解:连接OA,OB,如图所示:
∵六边形ABCDEF是正六边形,
∴∠AOB==60°,
当点P不在上时,
∠APB=∠AOB=30°,
当点P在上时,
∠APB=180°﹣∠AOB=180°﹣30°=150°,
故选:A.
5.解:连接OA,OB,OE,
∵正方形ABCD内接于⊙O,
∴OA=OB=OE,∠AOB==90°,AB=BC,∠ABC=90°,
∴∠OAB=∠OBA=(180°﹣∠AOB)=45°,
∴∠OBC=∠ABC﹣∠OBA=45°,
∵∠CBE=15°,
∴∠OBE=∠OBC+∠CBE=60°,
∴△OBE是等边三角形,
∴OB=BE=3,
∴OA=3,
∴AB==3,
∴BC=3,
故选:D.
6.解:∵在圆内接正六边形ABCDEF中,AB=AF=BC=CD,∠BAF=∠ABC=∠BCD=120°,
∴∠AFB=∠ABF=∠BAC=∠ACB=∠CBD=∠BDC=30°,
∴AG=BG,BH=CH,
∵∠GBH=∠BGH=∠BHG=60°,
∴AG=GH=BG=BH=CH,
连接OA,OB交AC于N,
则OB⊥AC,∠AOB=60°,
∵OA=15cm,
∴AN=OA=(cm),
∴AC=2AN=15(cm),
∴GH=AC=5(cm),
故选:B.
7.解:如图,连接GC并延长交BD于点H,连接AE,
∵ABCDEF正六边形,
∴AB=BC=CD=DE=EF=AF,
∠F=∠FAB=∠ABC=∠BCD=∠CDE=∠DEF=120°,
∴∠CBD=∠CDB=30°
∵△BDG是等边三角形,
∴BG=DG=BD,∠GBD=∠GDB=60°,
又CG=CG,
∴△BCG≌△DCG(SSS),
∵∠GBC=∠DBC=60°﹣30°=30°,
∴△GBC≌△DBC(SAS),
∴S△BCG=S△DCG=S△BCD=2,
∴S△AEF=2,
设CH=x,则BC=CG=2x,BH=x,
∴BD=2x,
∴CG BH=2,
即2x×x=2,
∴x2=2,
∴S四边形ABDE=AB BD=2x 2x=4x2=8,
∴五边形ABDEF的面积为:2+8=10.
故选:C.
8.解:连接OA、OB、OD,过O作OH⊥AB于H,如图所示:
则AH=BH=AB,
∵等边三角形ABC和正方形ADEF,都内接于⊙O,
∴∠AOB=120°,∠AOD=90°,
∵OA=OD=OB,
∴△AOD是等腰直角三角形,∠AOH=∠BOH=×120°=60°,
∴AD=OA,AH=OA sin60°=OA,
∴AB=2AH=2×OA=OA,
∴==,
故选:B.
9.解:∵A(1,0),O为正六边形的中心,
∴OA=AB=1,
连接OB,作BG⊥OA于点G,
则AG=OA=,BG=,
∴B(,),
∴C(﹣,),
E(﹣,﹣),
∵正六边形的边长=1,
∴正六边形的周长=6,
∵点P的速度为每秒1个单位长度,点Q的速度为每秒2个单位长度,
∴第1次相遇需要的时间为:6÷(1+2)=2(秒),
此时点P的路程为1×2=2,点Q的路程为2×2=4,
此时P,Q相遇地点的坐标在点C(﹣,),
以此类推:第二次相遇地点在点E(﹣,﹣),
第三次相遇地点在点A(1,0),
…如此下去,
∵2020÷3=673……1,
∴第2020次相遇地点在点C,C的坐标为(﹣,).
故选:A.
10.解:如图,
∵正方形MNKO和正六边形ABCDEF边长均为1
∴第一次旋转后点M1 纵坐标为,第二次、第三次旋转后点M2(M3)的纵坐标为﹣,四次旋转后点M4的纵坐标为﹣﹣,第五次旋转后点M5的纵坐标为+,第六次旋转后的点M6的纵坐标为.
故选:A.
11.解:∵S正六边形=6× a2=a2,S空白=2× a a=a2,
∴S阴=a2,
∴=,
故答案为:.
12.解:连接OA、OC、OD,如图所示:
∵点O为正六边形ABCDEF的中心,边长为2,
∴∠B=∠BCD=(6﹣2)×180°÷6=120°,OC=OD,∠COD==60°,AB=BC=CD=2,
∴∠BCA=∠BAC=30°,△OCD是等边三角形,
∴OC=CD=2,∠OCD=60°,
∴∠OCG=120°﹣30°﹣60°=30°,
∵OG⊥AC,
∴OG=OC=1,
即点O到AC的距离OG的长为1,
故答案为:1.
13.解:∵五边形ABCDE是正五边形,
∴∠CDE=∠E==108°,AE=DE,
∴∠EDA=∠EAD=(180°﹣∠E)=54°,
∴∠CDF=∠CDE﹣∠EDA=108°﹣36°=72°,
∵CF=CD,
∴∠CFD=∠CDF=72°,
故答案为:72.
14.解;连接AC、OE、OF,作OM⊥EF于M,
∵四边形ABCD是正方形,
∴AB=BC=4,∠ABC=90°,
∴AC是直径,AC=4,
∴OE=OF=2,∵OM⊥EF,
∴EM=MF,
∵△EFG是等边三角形,
∴∠GEF=60°,
在RT△OME中,∵OE=2,∠OEM=∠GEF=30°,
∴OM=,EM=OM=,
∴EF=2.
故答案为2.
15.解:当O、D、AB中点共线时,OD有最大值和最小值,
如图,BD=4,BK=2,
∴DK===2,OK=BK=2,
∴OD的最大值为:2+2,
同理,当O、D、AB中点共线时,将正六边形绕AB中点K旋转180°取得最小值为:2﹣2,
故答案为:2+2,2﹣2.
16.解:如图,取AB的中点K,以AB为直径作⊙K,
∵AF⊥BE,
∴∠AFB=90°,
∵AK=BK,
∴KF=AK=BK,
∵正方形ABCD的外接圆的半径为,
∴AB=BC==2,
∴KF=AK=KB=1,
∵∠CBK=90°,
∴CK===,
∵CF≥CK﹣KF,
∴CF≥﹣1,
∴CF的最小值为﹣1.
故答案为﹣1.
17.解:连接OB交AC于M,
∵正八边形ABCDEFGH内接于⊙O,
∴∠AOB=∠BOC==45°,AB=BC,
∴=,∠AOC=90°,
∴AM=CM=AC=2,OM⊥AC,
∵OA=OC,
∠OAM=∠OCA=(180°﹣∠AOC)=45°,
∴∠OAM=∠AOB,
∴AM=OM,
在Rt△AOC中,
∵OA=OC,OA2+OC2=AC2,
∴2OA2=AC2=42=16,
∴OA=2,
在Rt△AOM中,
∵OM2+AM2=OA2,
∴2OM2=(2)2,
∴OM=2,
∴点O到AC距离为2,
故答案为:2.
18.解:连接AD,作NM⊥PB于M,
∵六边形APCDEF是正六边形,
∴EF∥AD,DP⊥AB,DP⊥ED,正六边形的每一个内角为120°,
∴∠ADE=60°,
∴∠ADP=30°
∴PD=PA,
∵DP⊥AB,NM⊥PB
∴PD∥MN,
∴PM就是△PDN的PD边的高,
设PA=x.则PB=10﹣x,
∵在等腰△BPN中,MN⊥PB,
∴PM=PB=(10﹣x),
∴S△PDN=PD PM=×x×(10﹣x)=﹣(x﹣5)2+(0<x<10),
∴△PDN的面积的最大值为:.
故答案为:.
19.证明:(1)延长BP至E,使PE=PC,连接CE,如图1,
∵A、B、P、C四点共圆,
∴∠BAC+∠BPC=180°,
∵∠BPC+∠EPC=180°,
∴∠BAC=∠CPE=60°,
∵PE=PC,
∴△PCE是等边三角形,
∴CE=PC,∠E=60°;
又∵∠BCE=60°+∠BCP,∠ACP=60°+∠BCP,
∴∠BCE=∠ACP,
∵△ABC、△ECP为等边三角形,
∴CE=PC,AC=BC,
在△BEC和△APC中,
,
∴△BEC≌△APC(SAS),
∴PA=BE=PB+PC;
(2)过点B作BE⊥PB交PA于E,连接OA,OB.如图2,
∵∠1+∠2=∠2+∠3=90°
∴∠1=∠3,
∵∠APB=∠AOB=45°,
∴BP=BE,
∴PE=PB,
在△ABE和△CBP中,
,
∴△ABE≌△CBP(SAS),
∴PC=AE,
∴PA=AE+PE=PC+PB;
20.证明:(1)延长BP至E,使PE=PC,
连接CE.∵A、B、P、C四点共圆,
∴∠BAC+∠BPC=180°,
∵∠BPC+∠EPC=180°,
∴∠BAC=∠CPE=60°,PE=PC,
∴△PCE是等边三角形,
∴CE=PC,∠E=60°;
又∵∠BCE=60°+∠BCP,∠ACP=60°+∠BCP,
∴∠BCE=∠ACP,
∵△ABC、△ECP为等边三角形,
∴CE=PC,AC=BC,
∴△BEC≌△APC(SAS),
∴PA=BE=PB+PC.
(2)过点B作BE⊥PB交PA于E.
∵∠1+∠2=∠2+∠3=90°
∴∠1=∠3,
∴∠APB=45°,
∴BP=BE,∴;
又∵AB=BC,
∴△ABE≌△CBP,
∴PC=AE.
∴.
(3)答:;
证明:过点B,作BM⊥AP,在AP上截取AQ=PC,
连接BQ,∵∠BAP=∠BCP,AB=BC,
∴△ABQ≌△CBP,
∴BQ=BP.
∴MP=QM,
又∵∠APB=30°,
∴cos30°=,
∴PM=PB,
∴
∴
1.一个适当大的正六边形,它的一个顶点与一个边长为定值的小正六边形ABCDEF的中心O重合,且与边AB、CD相交于G、H(如图).图中阴影部分的面积记为S,三条线段GB、BC、CH的长度之和记为l,在大正六边形绕点O旋转过程中,下列说法正确的是( )
A.S变化,l不变 B.S不变,l变化
C.S变化,l变化 D.S与l均不变
2.如图,一个正六边形的一边长与它的一边相外切的圆的周长相等,当这个圆按箭头方向从某一位置沿正六边形的六边滚动,直至回到原出发位置时,则这个圆共转了( )
A.6圈 B.7圈 C.8圈 D.9圈
3.如图,已知正五边形ABCDE中,点F是BC的中点,P是线段EF上的动点,连接AP,BP,当AP+BP的值最小时,∠BPF的度数为( )
A.36° B.45° C.54° D.60°
4.如图,⊙O是正六边形ABCDEF的外接圆,点P在⊙O上(P不与A,B重合),则∠APB的度数为( )
A.30°或150° B.60°或120° C.30° D.60°
5.如图,正方形ABCD内接于⊙O.点E为上一点,连接BE、CE,若∠CBE=15°,BE=3,则BC的长为( )
A. B. C. D.
6.如图,在圆内接正六边形ABCDEF中,BF,BD分别交AC于点G,H.若该圆的半径为15cm,则线段GH的长为( )
A.cm B.5cm C.3cm D.10cm
7.如图,以正六边形ABCDEF的对角线BD为边,向右作等边三角形BDG,若四边形BCDG的面积为4,则五边形ABDEF的面积为( )
A.6 B.8 C.10 D.12
8.如图,等边三角形ABC和正方形ADEF都内接于⊙O,则AD:AB=( )
A.2: B.: C.: D.:2
9.如图,点O为正六边形的中心,P,Q分别从点A(1,0)同时出发,沿正六边形按图示方向运动,点P的速度为每秒1个单位长度,点Q的速度为每秒2个单位长度,则第2020次相遇地点的坐标为( )
A. B.(1,0) C. D.(﹣1,0)
10.已知正方形MNKO和正六边形ABCDEF边长均为1,把正方形放在正六边形外边,使OK边与AB边重合,如图所示,按下列步骤操作:将正方形在正六边形外绕点B顺时针旋转,使KN边与BC边重合,完成第一次旋转;再绕点C顺时针旋转,使NM边与CD边重合,完成第二次旋转;………在这样连续6次旋转的过程中,点M在图中直角坐标系中的纵坐标可能是( )
A. B.﹣2.2 C.2.3 D.﹣2.3
11.如图,边长为a的正六边形内有斜边为a、锐角为60°两个直角三角形,则= .
12.如图,点O为正六边形ABCDEF的中心,连接AC,若正六边形的边长为2,则点O到AC的距离OG的长为 .
13.如图,AD是正五边形ABCDE的一条对角线,以C为圆心,CB为半径画弧交AD于点F,连接CF,则∠CFD= °.
14.如图,正方形ABCD内接于⊙O,其边长为4,则⊙O的内接正三角形EFG的边长为 .
15.如图,正六边形ABCDEF的边长为4,两顶点A,B分别在x轴和y轴上运动,则顶点D到原点O的距离的最大值为 ;最小值为 .
16.如图,⊙O半径为,正方形ABCD内接于⊙O,点E在上运动,连接BE,作AF⊥BE,垂足为F,连接CF.则CF长的最小值为 .
17.如图,正八边形ABCDEFGH内接于⊙O,若AC=4,则点O到AC的距离为 .
18.如图所示,已知AB=10,点P是线段AB上的动点,以AP为边作正六边形APCDEF,以PB为底作等腰三角形BPN,连接PD,DN,则△PDN的面积的最大值是 .
19.(1)已知:如图1,△ABC是⊙O的内接正三角形,点P为劣弧BC上一动点.求证:PA=PB+PC;
(2)已知:如图2,四边形ABCD是⊙O的内接正方形,点P为劣弧BC上一动点.求证:PA=PC+PB.
20.(1)已知:如图1,△ABC是⊙O的内接正三角形,点P为弧BC上一动点,求证:PA=PB+PC;
(2)如图2,四边形ABCD是⊙O的内接正方形,点P为弧BC上一动点,求证:;
(3)如图3,六边形ABCDEF是⊙O的内接正六边形,点P为弧BC上一动点,请探究PA、PB、PC三者之间有何数量关系,并给予证明.
参考答案
1.解:如图,连接OA,OC.
∵∠HOB=∠AOC=120°,∠OCH=∠OAG=60°,
∴∠HOC=∠GOA,
在△OHC和△OGA中,
,
∴△HOC≌△GOA(ASA),
∴AG=CH,
∴S阴=S四边形OABC=定值,l=GB+BC+CH=AG+BG+BC=2BC=定值,
故选:D.
2.解:如图所示:
由切线的性质得:圆从一边旋转到另一边时,圆心要绕六边形的顶点旋转60°,
则圆绕6个顶点一共旋转了360°,即转了1圈,
∵正六边形的一边长与它的一边相外切的圆的周长相等,
∴圆在正六边形的6条边上滚动时要转6圈,
∴这个圆共转了7圈,
故选:B.
3.解:如图,连接AC,PC,设AC交EF于点P′,连接BP′.
∵正五边形ABCDE中,点F是BC的中点,
∵EF⊥BC,
∴B,C关于EF对称,
∴PB=PB,
∵PA+PB=PA+PC≥AC,
∴当点P与P′重合时,PA+PB的值最小,
∵ABCDE是正五边形,
∴BA=BC,∠ABC=108°,
∴∠BAC=∠BCA=36°,
∵P′B=CP′,
∴∠P′BC=∠P′CB=36°,
∵∠EFB=90°,
∴∠BP′F=90°﹣36°=54°.
故选:C.
4.解:连接OA,OB,如图所示:
∵六边形ABCDEF是正六边形,
∴∠AOB==60°,
当点P不在上时,
∠APB=∠AOB=30°,
当点P在上时,
∠APB=180°﹣∠AOB=180°﹣30°=150°,
故选:A.
5.解:连接OA,OB,OE,
∵正方形ABCD内接于⊙O,
∴OA=OB=OE,∠AOB==90°,AB=BC,∠ABC=90°,
∴∠OAB=∠OBA=(180°﹣∠AOB)=45°,
∴∠OBC=∠ABC﹣∠OBA=45°,
∵∠CBE=15°,
∴∠OBE=∠OBC+∠CBE=60°,
∴△OBE是等边三角形,
∴OB=BE=3,
∴OA=3,
∴AB==3,
∴BC=3,
故选:D.
6.解:∵在圆内接正六边形ABCDEF中,AB=AF=BC=CD,∠BAF=∠ABC=∠BCD=120°,
∴∠AFB=∠ABF=∠BAC=∠ACB=∠CBD=∠BDC=30°,
∴AG=BG,BH=CH,
∵∠GBH=∠BGH=∠BHG=60°,
∴AG=GH=BG=BH=CH,
连接OA,OB交AC于N,
则OB⊥AC,∠AOB=60°,
∵OA=15cm,
∴AN=OA=(cm),
∴AC=2AN=15(cm),
∴GH=AC=5(cm),
故选:B.
7.解:如图,连接GC并延长交BD于点H,连接AE,
∵ABCDEF正六边形,
∴AB=BC=CD=DE=EF=AF,
∠F=∠FAB=∠ABC=∠BCD=∠CDE=∠DEF=120°,
∴∠CBD=∠CDB=30°
∵△BDG是等边三角形,
∴BG=DG=BD,∠GBD=∠GDB=60°,
又CG=CG,
∴△BCG≌△DCG(SSS),
∵∠GBC=∠DBC=60°﹣30°=30°,
∴△GBC≌△DBC(SAS),
∴S△BCG=S△DCG=S△BCD=2,
∴S△AEF=2,
设CH=x,则BC=CG=2x,BH=x,
∴BD=2x,
∴CG BH=2,
即2x×x=2,
∴x2=2,
∴S四边形ABDE=AB BD=2x 2x=4x2=8,
∴五边形ABDEF的面积为:2+8=10.
故选:C.
8.解:连接OA、OB、OD,过O作OH⊥AB于H,如图所示:
则AH=BH=AB,
∵等边三角形ABC和正方形ADEF,都内接于⊙O,
∴∠AOB=120°,∠AOD=90°,
∵OA=OD=OB,
∴△AOD是等腰直角三角形,∠AOH=∠BOH=×120°=60°,
∴AD=OA,AH=OA sin60°=OA,
∴AB=2AH=2×OA=OA,
∴==,
故选:B.
9.解:∵A(1,0),O为正六边形的中心,
∴OA=AB=1,
连接OB,作BG⊥OA于点G,
则AG=OA=,BG=,
∴B(,),
∴C(﹣,),
E(﹣,﹣),
∵正六边形的边长=1,
∴正六边形的周长=6,
∵点P的速度为每秒1个单位长度,点Q的速度为每秒2个单位长度,
∴第1次相遇需要的时间为:6÷(1+2)=2(秒),
此时点P的路程为1×2=2,点Q的路程为2×2=4,
此时P,Q相遇地点的坐标在点C(﹣,),
以此类推:第二次相遇地点在点E(﹣,﹣),
第三次相遇地点在点A(1,0),
…如此下去,
∵2020÷3=673……1,
∴第2020次相遇地点在点C,C的坐标为(﹣,).
故选:A.
10.解:如图,
∵正方形MNKO和正六边形ABCDEF边长均为1
∴第一次旋转后点M1 纵坐标为,第二次、第三次旋转后点M2(M3)的纵坐标为﹣,四次旋转后点M4的纵坐标为﹣﹣,第五次旋转后点M5的纵坐标为+,第六次旋转后的点M6的纵坐标为.
故选:A.
11.解:∵S正六边形=6× a2=a2,S空白=2× a a=a2,
∴S阴=a2,
∴=,
故答案为:.
12.解:连接OA、OC、OD,如图所示:
∵点O为正六边形ABCDEF的中心,边长为2,
∴∠B=∠BCD=(6﹣2)×180°÷6=120°,OC=OD,∠COD==60°,AB=BC=CD=2,
∴∠BCA=∠BAC=30°,△OCD是等边三角形,
∴OC=CD=2,∠OCD=60°,
∴∠OCG=120°﹣30°﹣60°=30°,
∵OG⊥AC,
∴OG=OC=1,
即点O到AC的距离OG的长为1,
故答案为:1.
13.解:∵五边形ABCDE是正五边形,
∴∠CDE=∠E==108°,AE=DE,
∴∠EDA=∠EAD=(180°﹣∠E)=54°,
∴∠CDF=∠CDE﹣∠EDA=108°﹣36°=72°,
∵CF=CD,
∴∠CFD=∠CDF=72°,
故答案为:72.
14.解;连接AC、OE、OF,作OM⊥EF于M,
∵四边形ABCD是正方形,
∴AB=BC=4,∠ABC=90°,
∴AC是直径,AC=4,
∴OE=OF=2,∵OM⊥EF,
∴EM=MF,
∵△EFG是等边三角形,
∴∠GEF=60°,
在RT△OME中,∵OE=2,∠OEM=∠GEF=30°,
∴OM=,EM=OM=,
∴EF=2.
故答案为2.
15.解:当O、D、AB中点共线时,OD有最大值和最小值,
如图,BD=4,BK=2,
∴DK===2,OK=BK=2,
∴OD的最大值为:2+2,
同理,当O、D、AB中点共线时,将正六边形绕AB中点K旋转180°取得最小值为:2﹣2,
故答案为:2+2,2﹣2.
16.解:如图,取AB的中点K,以AB为直径作⊙K,
∵AF⊥BE,
∴∠AFB=90°,
∵AK=BK,
∴KF=AK=BK,
∵正方形ABCD的外接圆的半径为,
∴AB=BC==2,
∴KF=AK=KB=1,
∵∠CBK=90°,
∴CK===,
∵CF≥CK﹣KF,
∴CF≥﹣1,
∴CF的最小值为﹣1.
故答案为﹣1.
17.解:连接OB交AC于M,
∵正八边形ABCDEFGH内接于⊙O,
∴∠AOB=∠BOC==45°,AB=BC,
∴=,∠AOC=90°,
∴AM=CM=AC=2,OM⊥AC,
∵OA=OC,
∠OAM=∠OCA=(180°﹣∠AOC)=45°,
∴∠OAM=∠AOB,
∴AM=OM,
在Rt△AOC中,
∵OA=OC,OA2+OC2=AC2,
∴2OA2=AC2=42=16,
∴OA=2,
在Rt△AOM中,
∵OM2+AM2=OA2,
∴2OM2=(2)2,
∴OM=2,
∴点O到AC距离为2,
故答案为:2.
18.解:连接AD,作NM⊥PB于M,
∵六边形APCDEF是正六边形,
∴EF∥AD,DP⊥AB,DP⊥ED,正六边形的每一个内角为120°,
∴∠ADE=60°,
∴∠ADP=30°
∴PD=PA,
∵DP⊥AB,NM⊥PB
∴PD∥MN,
∴PM就是△PDN的PD边的高,
设PA=x.则PB=10﹣x,
∵在等腰△BPN中,MN⊥PB,
∴PM=PB=(10﹣x),
∴S△PDN=PD PM=×x×(10﹣x)=﹣(x﹣5)2+(0<x<10),
∴△PDN的面积的最大值为:.
故答案为:.
19.证明:(1)延长BP至E,使PE=PC,连接CE,如图1,
∵A、B、P、C四点共圆,
∴∠BAC+∠BPC=180°,
∵∠BPC+∠EPC=180°,
∴∠BAC=∠CPE=60°,
∵PE=PC,
∴△PCE是等边三角形,
∴CE=PC,∠E=60°;
又∵∠BCE=60°+∠BCP,∠ACP=60°+∠BCP,
∴∠BCE=∠ACP,
∵△ABC、△ECP为等边三角形,
∴CE=PC,AC=BC,
在△BEC和△APC中,
,
∴△BEC≌△APC(SAS),
∴PA=BE=PB+PC;
(2)过点B作BE⊥PB交PA于E,连接OA,OB.如图2,
∵∠1+∠2=∠2+∠3=90°
∴∠1=∠3,
∵∠APB=∠AOB=45°,
∴BP=BE,
∴PE=PB,
在△ABE和△CBP中,
,
∴△ABE≌△CBP(SAS),
∴PC=AE,
∴PA=AE+PE=PC+PB;
20.证明:(1)延长BP至E,使PE=PC,
连接CE.∵A、B、P、C四点共圆,
∴∠BAC+∠BPC=180°,
∵∠BPC+∠EPC=180°,
∴∠BAC=∠CPE=60°,PE=PC,
∴△PCE是等边三角形,
∴CE=PC,∠E=60°;
又∵∠BCE=60°+∠BCP,∠ACP=60°+∠BCP,
∴∠BCE=∠ACP,
∵△ABC、△ECP为等边三角形,
∴CE=PC,AC=BC,
∴△BEC≌△APC(SAS),
∴PA=BE=PB+PC.
(2)过点B作BE⊥PB交PA于E.
∵∠1+∠2=∠2+∠3=90°
∴∠1=∠3,
∴∠APB=45°,
∴BP=BE,∴;
又∵AB=BC,
∴△ABE≌△CBP,
∴PC=AE.
∴.
(3)答:;
证明:过点B,作BM⊥AP,在AP上截取AQ=PC,
连接BQ,∵∠BAP=∠BCP,AB=BC,
∴△ABQ≌△CBP,
∴BQ=BP.
∴MP=QM,
又∵∠APB=30°,
∴cos30°=,
∴PM=PB,
∴
∴
