2021-2022学年冀教版七年级数学上册4.4 整式的加减 同步测试卷(word版含答案)
文档属性
| 名称 | 2021-2022学年冀教版七年级数学上册4.4 整式的加减 同步测试卷(word版含答案) | 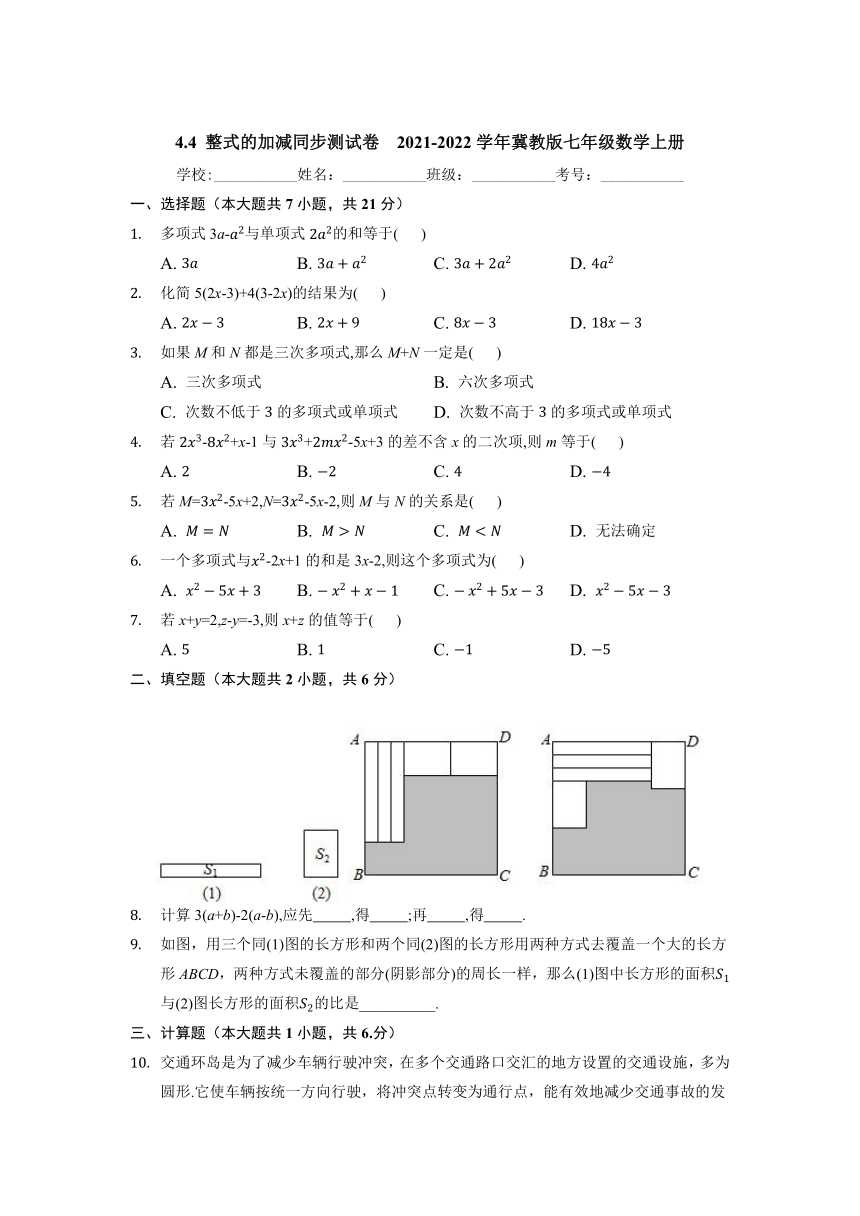 | |
| 格式 | docx | ||
| 文件大小 | 70.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-05 17:07:21 | ||
图片预览





文档简介
4.4 整式的加减同步测试卷 2021-2022学年冀教版七年级数学上册
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共7小题,共21分)
多项式3a-与单项式的和等于( )
A. B. C. D.
化简5(2x-3)+4(3-2x)的结果为( )
A. B. C. D.
如果M和N都是三次多项式,那么M+N一定是( )
A. 三次多项式 B. 六次多项式
C. 次数不低于的多项式或单项式 D. 次数不高于的多项式或单项式
若-+x-1与+-5x+3的差不含x的二次项,则m等于( )
A. B. C. D.
若M=-5x+2,N=-5x-2,则M与N的关系是( )
A. B. C. D. 无法确定
一个多项式与-2x+1的和是3x-2,则这个多项式为( )
A. B. C. D.
若x+y=2,z-y=-3,则x+z的值等于( )
A. B. C. D.
二、填空题(本大题共2小题,共6分)
计算3(a+b)-2(a-b),应先 ,得 ;再 ,得 .
如图,用三个同(1)图的长方形和两个同(2)图的长方形用两种方式去覆盖一个大的长方形ABCD,两种方式未覆盖的部分(阴影部分)的周长一样,那么(1)图中长方形的面积与(2)图长方形的面积的比是__________.
三、计算题(本大题共1小题,共6.分)
交通环岛是为了减少车辆行驶冲突,在多个交通路口交汇的地方设置的交通设施,多为圆形.它使车辆按统一方向行驶,将冲突点转变为通行点,能有效地减少交通事故的发生.如图所示的是某交通环岛的简化模型(因路段FG施工,禁止从路段EF行驶过来的车辆在环岛内通行,只能往环岛外行驶),某时段内该交通环岛的进出机动车辆数如图所示,图中箭头方向表示车辆的行驶方向.
(1)求该时段内路段AB上的机动车辆数x1;
(2)求该时段内从F口驶出的机动车辆数x2;
(3)若,,求该时段内路段CD上的机动车辆数x3.
四、解答题(本大题共10小题,共87分)
(1)当x=1时,多项式+qx+1的值为2023,求当x=-1时,多项式+qx+1的值;
(2)求当式子+5取最小值时,式子5x-[--(-5x+2)]的值.
先化简,再求值.
(1)已知:-2(mn-)+[-5(mn-)+2mn],其中m,n满足|m-1|+=0;
(2)-+(-)-2(-),其中a,b满足|a+1|与|b+2|互为相反数.
已知x+4y=-1,xy=-5,求(6xy+7y)+[9x-(5xy-y+7x)]的值.
当多项式--(2m-1)+(2-3n)x-1不含二次项和一次项时,求m-2n的值.
小明做一道数学题:“已知两个多项式A,B,A=B=+3x-2,计算3A+B.”小明误把“3A+B”看成“A+3B”,求得的结果为-2x+3,请求出3A+B的正确结果.
已知A=+xy+3y-1,B=-xy.
(1)若+|y-3|=0,求A-2B的值;
(2)若A-2B的值与y的值无关,求x的值.
已知k为常数,化简关于x的式子(+x)-[-(-x+1)],并求出当k为何值时,此式子的值为定值 定值是多少
为了加强公民的节水意识,合理利用水资源,某市采用价格调控的手段达到节水的目的,该市自来水收费的价目表如下(注:水费按月份结算,表示立方米):
价目表
每月用水量 价格
不超过的部分 2元/
超出不超出的部分 4元/
超出的部分 8元/
请根据上表的内容解答下列问题:
(1)填空:若某户居民2月份用水,则应收水费 元;
(2)若该户居民3月份用水(其中6< a 10),则应收水费多少元 (用含a的代数式表示,并化简)
(3)若该户居民4、5两个月共用水(5月份用水量超过了4月份),设4月份用水,求该户居民4、5两个月共交水费多少元.(用含x的代数式表示,并化简)
如图是某月的月历.
(1)带阴影的十字框中的5个数之和与十字框中心的数有什么关系
(2)不改变十字框的大小,如果将带阴影的十字框移至其他几个位置试一试,你能得出什么结论 你知道为什么吗
(3)这个结论对于任何一个月的月历都成立吗
20.某电器商销售一种微波炉和电磁炉,微波炉每台定价800元,电磁炉每台定价200元.“十一”期间商场决定开展促销活动,活动期间向客户提供两种优惠方案.
方案一:买一台微波炉送一台电磁炉;
方案二:微波炉和电磁炉都按定价的90%付款.
现某客户要到该卖场购买微波炉10台,电磁炉x台(x>10).
(1)若该客户按方案一购买,需付款______元.(用含x的代数式表示)若该客户按方案二购买,需付款______元.(用含x的代数式表示)
(2)若x=30,通过计算说明此时按哪种方案购买较为合算?
(3)当x=30时,你能给出一种更为省钱的购买方案吗?试写出你的购买方法.并计算需付款多少元?
1.【答案】B
2.【答案】A
3.【答案】D
4.【答案】D
5.【答案】B
6.【答案】C
7.【答案】C
8.【答案】去括号 3a+3b-2a+2b 合并同类项 a+5b
9.【答案】2:3
10.【答案】解:(1)根据题意得:a-b+a+b=2a,
则该时段内路段AB上的机动车辆数x1有2a台;
(2)根据题意得:x3=x1-(a-b)+2b=a+3b,x2=x3-a+2a=2a+3b,
则该时段内从F口驶出的机动车辆x2有(2a+3b);
(3)当a=10,b=4时,原式=10+12=22(台),
则该时段内路段CD上的机动车辆处x3有22台.
11.【答案】解:(1)因为当x=1时,多项式+qx+1的值为2023,所以p+q1+1=2023,
则p+q=2022.
当x=-1时,+qx+1=p+q(-1)+1
=-p-q+1=-(p+q)+1=-2022+1=-2021.
(2)因为+5取得最小值时,=0,
所以2x+4=0,
解得x=-2.
原式=5x-(-+5x-2)=5x+-5x+2=+2.
当x=-2时,原式=2+2=10.
12.【答案】解:(1)原式=-2mn++-5mn++2mn
=-5mn,
由|m-1|+=0,
得m-1=0,n+2=0,
即m=1,n=-2.
当m=1,n=-2时,
原式=-5mn
=12-51(-2)
=22.
(2)原式=-+--+
=-.
因为|a+1|与|b+2|互为相反数,
所以|a+1|+|b+2|=0,
即a+1=0,b+2=0,
即a=-1,b=-2.
当a=-1,b=-2时,
原式=-
=-(-1)
=4.
13.【答案】解:原式=6xy+7y+9x-5xy+y-7x
=xy+8y+2x
=xy+2(x+4y).
当x+4y=-1,xy=-5时,
原式=xy+2(x+4y)=-5-2=-7.
14.【答案】解:由题意,得2m-1=0,2-3n=0,
解得m=,n=.
当m=,n=时,
m-2n=-2=-.
15.【答案】解:A=-2x+3-3(+3x-2)
=-2x+3--9x+6
=-11x+9.
3A+B=3(-11x+9)++3x-2
=-33x+27++3x-2
=-30x+25.
16.【答案】解:(1)因为+|y-3|=0,
所以x+2=0,y-3=0,
即x=-2,y=3.
A-2B=+xy+3y-1-2(-xy)
=+xy+3y-1-+2xy
=3xy+3y-1.
当x=-2,y=3时,
原式=3xy+3y-1
=3(-2)3+33-1
=-10.
(2)因为A-2B=3xy+3y-1=(3x+3)y-1,A-2B的值与y的值无关,
所以3x+3=0,则x=-1,
即x的值是-1.
17.【答案】解:原式=+x-+-x+1=(3-k)+1,
当k=3时,
原式=1.
所以当k=3时,此式子的值为定值,此定值为1.
18.【答案】解:(1)8.
24=8(元).
(2)4(a-6)+62=(4a-12)元,所以应收水费(4a-12)元.
(3)因为5月份用水量超过了4月份,所以4月份用水量少于7..
当4月份用水量少于时,5月份用水量超过,
所以4、5月份共交水费2x+8(15-x-10)+44+62=(-6x+68)元;
当4月份用水量大于或等于但不超过时,5月份用水量不少于但不超过,
所以4、5月份共交水费2x+4(15-x-6)+62=(-2x+48)元;
当4月份用水量超过且少于7.时,5月份用水量超过7.但少于,
所以4、5月份共交水费4(x-6)+62+4(15-x-6)+62=36(元).
19.【答案】解:(1)带阴影的十字框中的5个数之和是十字框中心的数的5倍.
(2)带阴影的十字框中的5个数之和是十字框中心的数的5倍,
理由如下:设十字框中心的数为x,则其余4个数分别为x-7,x-1,x+1,x+7,带阴影的十字框中的5个数之和为(x-7)+(x-1)+x+(x+1)+(x+7)=5x,所以带阴影的十字框中的5个数之和是十字框中心的数的5倍.
(3)这个结论对于任何一个月的月历都成立.
20.【答案】(1)(200x+6000) (180x+7200)
(2) 当x=30时,方案一:200×30+6000=12000(元),
方案二:180×30+7200=12600(元),
所以,按方案一购买较合算.
(3)先按方案一购买10台微波炉送10台电磁炉,再按方案二购买20台微波炉,
共10×800+200×20×90%=11600(元).
第2页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共7小题,共21分)
多项式3a-与单项式的和等于( )
A. B. C. D.
化简5(2x-3)+4(3-2x)的结果为( )
A. B. C. D.
如果M和N都是三次多项式,那么M+N一定是( )
A. 三次多项式 B. 六次多项式
C. 次数不低于的多项式或单项式 D. 次数不高于的多项式或单项式
若-+x-1与+-5x+3的差不含x的二次项,则m等于( )
A. B. C. D.
若M=-5x+2,N=-5x-2,则M与N的关系是( )
A. B. C. D. 无法确定
一个多项式与-2x+1的和是3x-2,则这个多项式为( )
A. B. C. D.
若x+y=2,z-y=-3,则x+z的值等于( )
A. B. C. D.
二、填空题(本大题共2小题,共6分)
计算3(a+b)-2(a-b),应先 ,得 ;再 ,得 .
如图,用三个同(1)图的长方形和两个同(2)图的长方形用两种方式去覆盖一个大的长方形ABCD,两种方式未覆盖的部分(阴影部分)的周长一样,那么(1)图中长方形的面积与(2)图长方形的面积的比是__________.
三、计算题(本大题共1小题,共6.分)
交通环岛是为了减少车辆行驶冲突,在多个交通路口交汇的地方设置的交通设施,多为圆形.它使车辆按统一方向行驶,将冲突点转变为通行点,能有效地减少交通事故的发生.如图所示的是某交通环岛的简化模型(因路段FG施工,禁止从路段EF行驶过来的车辆在环岛内通行,只能往环岛外行驶),某时段内该交通环岛的进出机动车辆数如图所示,图中箭头方向表示车辆的行驶方向.
(1)求该时段内路段AB上的机动车辆数x1;
(2)求该时段内从F口驶出的机动车辆数x2;
(3)若,,求该时段内路段CD上的机动车辆数x3.
四、解答题(本大题共10小题,共87分)
(1)当x=1时,多项式+qx+1的值为2023,求当x=-1时,多项式+qx+1的值;
(2)求当式子+5取最小值时,式子5x-[--(-5x+2)]的值.
先化简,再求值.
(1)已知:-2(mn-)+[-5(mn-)+2mn],其中m,n满足|m-1|+=0;
(2)-+(-)-2(-),其中a,b满足|a+1|与|b+2|互为相反数.
已知x+4y=-1,xy=-5,求(6xy+7y)+[9x-(5xy-y+7x)]的值.
当多项式--(2m-1)+(2-3n)x-1不含二次项和一次项时,求m-2n的值.
小明做一道数学题:“已知两个多项式A,B,A=B=+3x-2,计算3A+B.”小明误把“3A+B”看成“A+3B”,求得的结果为-2x+3,请求出3A+B的正确结果.
已知A=+xy+3y-1,B=-xy.
(1)若+|y-3|=0,求A-2B的值;
(2)若A-2B的值与y的值无关,求x的值.
已知k为常数,化简关于x的式子(+x)-[-(-x+1)],并求出当k为何值时,此式子的值为定值 定值是多少
为了加强公民的节水意识,合理利用水资源,某市采用价格调控的手段达到节水的目的,该市自来水收费的价目表如下(注:水费按月份结算,表示立方米):
价目表
每月用水量 价格
不超过的部分 2元/
超出不超出的部分 4元/
超出的部分 8元/
请根据上表的内容解答下列问题:
(1)填空:若某户居民2月份用水,则应收水费 元;
(2)若该户居民3月份用水(其中6< a 10),则应收水费多少元 (用含a的代数式表示,并化简)
(3)若该户居民4、5两个月共用水(5月份用水量超过了4月份),设4月份用水,求该户居民4、5两个月共交水费多少元.(用含x的代数式表示,并化简)
如图是某月的月历.
(1)带阴影的十字框中的5个数之和与十字框中心的数有什么关系
(2)不改变十字框的大小,如果将带阴影的十字框移至其他几个位置试一试,你能得出什么结论 你知道为什么吗
(3)这个结论对于任何一个月的月历都成立吗
20.某电器商销售一种微波炉和电磁炉,微波炉每台定价800元,电磁炉每台定价200元.“十一”期间商场决定开展促销活动,活动期间向客户提供两种优惠方案.
方案一:买一台微波炉送一台电磁炉;
方案二:微波炉和电磁炉都按定价的90%付款.
现某客户要到该卖场购买微波炉10台,电磁炉x台(x>10).
(1)若该客户按方案一购买,需付款______元.(用含x的代数式表示)若该客户按方案二购买,需付款______元.(用含x的代数式表示)
(2)若x=30,通过计算说明此时按哪种方案购买较为合算?
(3)当x=30时,你能给出一种更为省钱的购买方案吗?试写出你的购买方法.并计算需付款多少元?
1.【答案】B
2.【答案】A
3.【答案】D
4.【答案】D
5.【答案】B
6.【答案】C
7.【答案】C
8.【答案】去括号 3a+3b-2a+2b 合并同类项 a+5b
9.【答案】2:3
10.【答案】解:(1)根据题意得:a-b+a+b=2a,
则该时段内路段AB上的机动车辆数x1有2a台;
(2)根据题意得:x3=x1-(a-b)+2b=a+3b,x2=x3-a+2a=2a+3b,
则该时段内从F口驶出的机动车辆x2有(2a+3b);
(3)当a=10,b=4时,原式=10+12=22(台),
则该时段内路段CD上的机动车辆处x3有22台.
11.【答案】解:(1)因为当x=1时,多项式+qx+1的值为2023,所以p+q1+1=2023,
则p+q=2022.
当x=-1时,+qx+1=p+q(-1)+1
=-p-q+1=-(p+q)+1=-2022+1=-2021.
(2)因为+5取得最小值时,=0,
所以2x+4=0,
解得x=-2.
原式=5x-(-+5x-2)=5x+-5x+2=+2.
当x=-2时,原式=2+2=10.
12.【答案】解:(1)原式=-2mn++-5mn++2mn
=-5mn,
由|m-1|+=0,
得m-1=0,n+2=0,
即m=1,n=-2.
当m=1,n=-2时,
原式=-5mn
=12-51(-2)
=22.
(2)原式=-+--+
=-.
因为|a+1|与|b+2|互为相反数,
所以|a+1|+|b+2|=0,
即a+1=0,b+2=0,
即a=-1,b=-2.
当a=-1,b=-2时,
原式=-
=-(-1)
=4.
13.【答案】解:原式=6xy+7y+9x-5xy+y-7x
=xy+8y+2x
=xy+2(x+4y).
当x+4y=-1,xy=-5时,
原式=xy+2(x+4y)=-5-2=-7.
14.【答案】解:由题意,得2m-1=0,2-3n=0,
解得m=,n=.
当m=,n=时,
m-2n=-2=-.
15.【答案】解:A=-2x+3-3(+3x-2)
=-2x+3--9x+6
=-11x+9.
3A+B=3(-11x+9)++3x-2
=-33x+27++3x-2
=-30x+25.
16.【答案】解:(1)因为+|y-3|=0,
所以x+2=0,y-3=0,
即x=-2,y=3.
A-2B=+xy+3y-1-2(-xy)
=+xy+3y-1-+2xy
=3xy+3y-1.
当x=-2,y=3时,
原式=3xy+3y-1
=3(-2)3+33-1
=-10.
(2)因为A-2B=3xy+3y-1=(3x+3)y-1,A-2B的值与y的值无关,
所以3x+3=0,则x=-1,
即x的值是-1.
17.【答案】解:原式=+x-+-x+1=(3-k)+1,
当k=3时,
原式=1.
所以当k=3时,此式子的值为定值,此定值为1.
18.【答案】解:(1)8.
24=8(元).
(2)4(a-6)+62=(4a-12)元,所以应收水费(4a-12)元.
(3)因为5月份用水量超过了4月份,所以4月份用水量少于7..
当4月份用水量少于时,5月份用水量超过,
所以4、5月份共交水费2x+8(15-x-10)+44+62=(-6x+68)元;
当4月份用水量大于或等于但不超过时,5月份用水量不少于但不超过,
所以4、5月份共交水费2x+4(15-x-6)+62=(-2x+48)元;
当4月份用水量超过且少于7.时,5月份用水量超过7.但少于,
所以4、5月份共交水费4(x-6)+62+4(15-x-6)+62=36(元).
19.【答案】解:(1)带阴影的十字框中的5个数之和是十字框中心的数的5倍.
(2)带阴影的十字框中的5个数之和是十字框中心的数的5倍,
理由如下:设十字框中心的数为x,则其余4个数分别为x-7,x-1,x+1,x+7,带阴影的十字框中的5个数之和为(x-7)+(x-1)+x+(x+1)+(x+7)=5x,所以带阴影的十字框中的5个数之和是十字框中心的数的5倍.
(3)这个结论对于任何一个月的月历都成立.
20.【答案】(1)(200x+6000) (180x+7200)
(2) 当x=30时,方案一:200×30+6000=12000(元),
方案二:180×30+7200=12600(元),
所以,按方案一购买较合算.
(3)先按方案一购买10台微波炉送10台电磁炉,再按方案二购买20台微波炉,
共10×800+200×20×90%=11600(元).
第2页,共2页
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
