2021-2022学年人教版数学八年级上册14.2.2完全平方公式课堂专练(word版、含解析)
文档属性
| 名称 | 2021-2022学年人教版数学八年级上册14.2.2完全平方公式课堂专练(word版、含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 167.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-05 16:59:51 | ||
图片预览

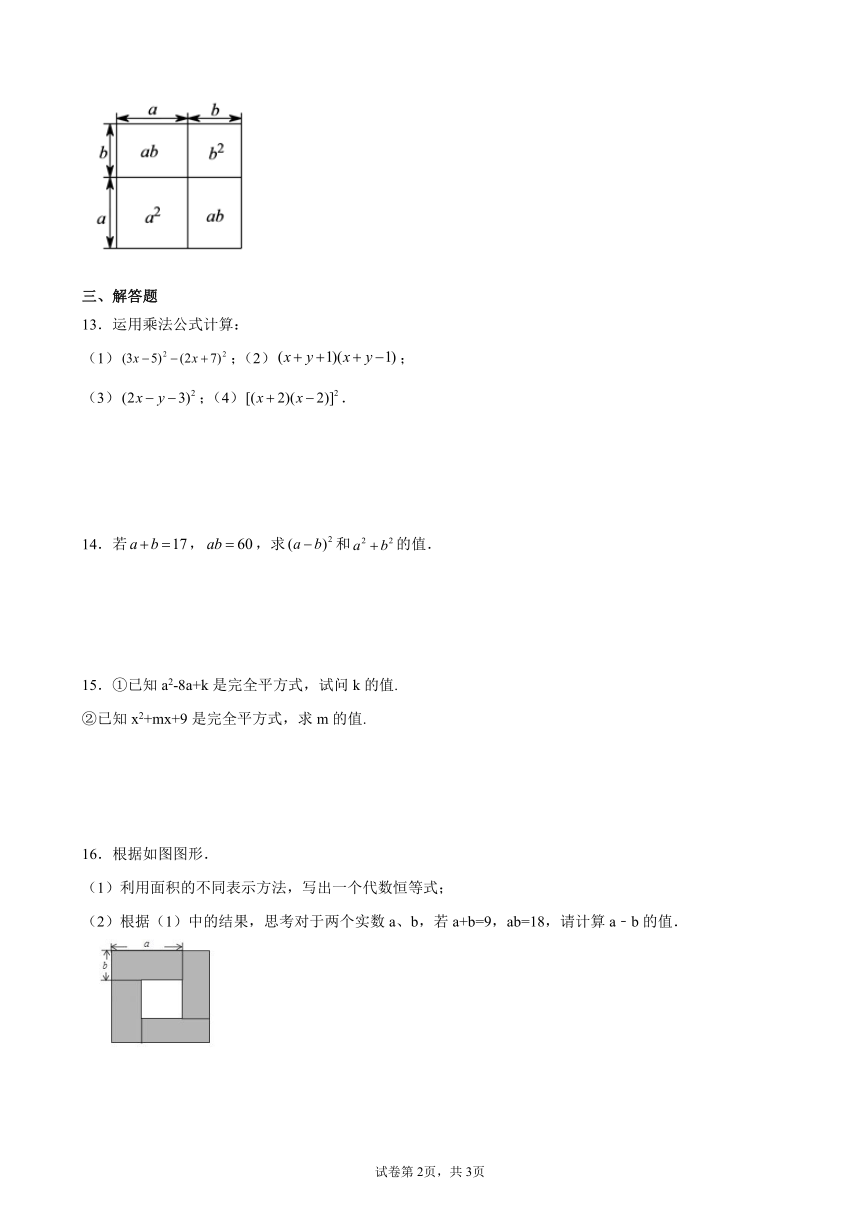

文档简介
2021-2022学年初中(人教版)数学八年级上册
14.2.2完全平方公式-课堂专练
时间:40分钟
一、单选题
1.已知,则代数式的值是( )
A. B. C. D.
2.若多项式是一个完全平方式,则m的值为( )
A.12 B. C.6 D.
3.已知无论x取何值,等式恒成立,则关于代数式的值有下列结论:①交换a,b的位置,代数式的值不变;②该代数式的值是非正数;③该代数式的值不会小于-2,上述结论正确的是( )
A.①② B.①③ C.②③ D.①②③
4.正方形的边长增加了,面积相应增加了,则这个正方形原来的面积是( )
A. B. C. D.
5.代数式(m﹣2)(m+2)(m2+4)﹣(m4﹣16)的结果为( )
A.0 B.4m C.﹣4m D.2m4
6.在Rt△ABC中,a,b为直角边,c为斜边.若a+b=21,c=15,则△ABC的面积是
A.25 B.54 C.63 D.无法确定
二、填空题
7.(1)________=(________-5)2;
(2)________=(x-________)2.
8.化简的结果是________.
9.已知正方形的面积是9a2+6a+1(a>0),则该正方形的边长是_________.
10. (3x+____)2=________________;
11.若,,则__________.
12.如图,最大正方形的面积可用两种形式表示:①__________;②__________,这两个代数式表示同一块面积,由此得到完全平方公式__________.
三、解答题
13.运用乘法公式计算:
(1);(2);
(3);(4).
14.若,,求和的值.
15.①已知a2-8a+k是完全平方式,试问k的值.
②已知x2+mx+9是完全平方式,求m的值.
16.根据如图图形.
(1)利用面积的不同表示方法,写出一个代数恒等式;
(2)根据(1)中的结果,思考对于两个实数a、b,若a+b=9,ab=18,请计算a﹣b的值.
17.如图所示,成都市青羊区有一块长为米,宽为米的长方形地块,角上有四个边长均为米的小正方形空地,开发商计划将阴影部分进行绿化.
(1)用含,的代数式表示绿化的面积是多少平方米?(结果写成最简形式)
(2)若,,求出绿化面积.
试卷第2页,共2页
试卷第1页,共1页
参考答案
1.A
【解析】解:
,
∵a+2b=m,
∴原式,
故选:A.
2.B
【解析】解:∵9x2-mx+4是一个完全平方式,
∴-m=±12,
∴m=±12.
故选:B.
3.A
【解析】解:∵等式(x+a)(x+b)=x2+2x+n恒成立,
即x2+(a+b)x+ab=x2+2x+n恒成立,
∴,
∴a3b+ab3-2
=ab(a2+b2)-2
=ab[(a+b)2-2ab]-2
=n[22-2n]-2
=4n-2n2-2
=-2n2+4n-2
=-2(n-1)2≤0,
∵-2(n-1)2中只与n有关,故①正确;
根据偶次幂为非负数得:-2(n-1)2≤0,故②正确,③错误;
故选:A.
4.B
【解析】设原来正方形的边长为xcm,增加后边长为(x+2)cm,
根据题意得:(x+2)2-x2=24,
x2+4x+4-x2=24,
4x=20
解得:x=5,
正方形原来的面积是5×5=25cm2.
故选B.
5.A
【解析】解:(m﹣2)(m+2)(m2+4)﹣(m4﹣16)
=(m2﹣4)(m2+4)﹣(m4﹣16)
=(m4﹣16)﹣(m4﹣16)
=0.
故选:A.
6.B
【解析】∵a+b=21,c=15,
∴(a+b)2=441,即a2+b2+2ab=441,
又∵a2+b2=c2=225,
∴2ab=216,
∴ab=54,
即S△ABC=54.
故选B.
7.25
【解析】解:(1),即:,
(2),即:,
故答案为:(1)25;;(2);.
8.-4x-8x+10
【解析】原式=-x+2x-3x-5x-5x+10=-4x-8x+10
故答案为-4x-8x+10
9.3a+1
【解析】解:∵9a2+6a+1=(3a+1)2,
由题可知9a2+6a+1(a>0)是正方形的面积,
∴该正方形的边长是3a+1.
10.2 4
【解析】,
故答案为:,,.
11.
【解析】∵,,
∴=9+4=13,
故答案为:13.
12.; ;
【解析】根据正方形面积公式可得:,正方形面积等于两个小正方形的面积和两个长方形面积之和,即,所以,答案为:, ,.
13.(1);(2);(3);(4).
【解析】解:(1)原式=[(3x 5)+(2x+7)][(3x 5) (2x+7)]
=(3x 5+2x+7)(3x 5 2x 7)
=(5x+2)(x 12)
=;
(2)原式=[(x+y)+1][(x+y) 1]
= 1
=;
(3)原式=
= 6(2x y)+9
=;
(4)原式=
=.
14.49,169
【解析】,,
15.①k=16; ②m=±6.
【解析】①设m2=k;因为a2-8a+k是完全平方式,
所以a2-8a+m2=(a-m)2= a2-2ma+m2,
所以8a=2ma,
解得m=4,
所以k=16;
②因为x2+mx+9是完全平方式,
所以x2+mx+9=(x±3)2,
所以m=±6.
16.(1)(a+b)2=(a﹣b)2+4ab;(2)a﹣b=3.
【解析】(1)根据题意得:
(a+b)2=(a﹣b)2+4ab.
(2)由(1)得(a+b)2=(a﹣b)2+4ab
∴(a﹣b)2=(a+b)2﹣4ab.
当a+b=9,ab=18时,(a﹣b)2=92﹣4×18=9,
∴a﹣b=±
∵a>b
∴a﹣b=3.
17.(1)-7b2+12ab;(2)1700平方米.
【解析】解:(1)(2a+3b)(2a-b)-4(a-b)2=4a2+4ab-3b2-4a2+8ab-4b2=-7b2+12ab;
答:绿化的面积是(-7b2+12ab)平方米;
(2)把a=20,b=10代入-7b2+12ab得,-7×102+12×20×10=1700平方米,
答:绿化面积为1700平方米.
答案第1页,共2页
答案第1页,共2页
14.2.2完全平方公式-课堂专练
时间:40分钟
一、单选题
1.已知,则代数式的值是( )
A. B. C. D.
2.若多项式是一个完全平方式,则m的值为( )
A.12 B. C.6 D.
3.已知无论x取何值,等式恒成立,则关于代数式的值有下列结论:①交换a,b的位置,代数式的值不变;②该代数式的值是非正数;③该代数式的值不会小于-2,上述结论正确的是( )
A.①② B.①③ C.②③ D.①②③
4.正方形的边长增加了,面积相应增加了,则这个正方形原来的面积是( )
A. B. C. D.
5.代数式(m﹣2)(m+2)(m2+4)﹣(m4﹣16)的结果为( )
A.0 B.4m C.﹣4m D.2m4
6.在Rt△ABC中,a,b为直角边,c为斜边.若a+b=21,c=15,则△ABC的面积是
A.25 B.54 C.63 D.无法确定
二、填空题
7.(1)________=(________-5)2;
(2)________=(x-________)2.
8.化简的结果是________.
9.已知正方形的面积是9a2+6a+1(a>0),则该正方形的边长是_________.
10. (3x+____)2=________________;
11.若,,则__________.
12.如图,最大正方形的面积可用两种形式表示:①__________;②__________,这两个代数式表示同一块面积,由此得到完全平方公式__________.
三、解答题
13.运用乘法公式计算:
(1);(2);
(3);(4).
14.若,,求和的值.
15.①已知a2-8a+k是完全平方式,试问k的值.
②已知x2+mx+9是完全平方式,求m的值.
16.根据如图图形.
(1)利用面积的不同表示方法,写出一个代数恒等式;
(2)根据(1)中的结果,思考对于两个实数a、b,若a+b=9,ab=18,请计算a﹣b的值.
17.如图所示,成都市青羊区有一块长为米,宽为米的长方形地块,角上有四个边长均为米的小正方形空地,开发商计划将阴影部分进行绿化.
(1)用含,的代数式表示绿化的面积是多少平方米?(结果写成最简形式)
(2)若,,求出绿化面积.
试卷第2页,共2页
试卷第1页,共1页
参考答案
1.A
【解析】解:
,
∵a+2b=m,
∴原式,
故选:A.
2.B
【解析】解:∵9x2-mx+4是一个完全平方式,
∴-m=±12,
∴m=±12.
故选:B.
3.A
【解析】解:∵等式(x+a)(x+b)=x2+2x+n恒成立,
即x2+(a+b)x+ab=x2+2x+n恒成立,
∴,
∴a3b+ab3-2
=ab(a2+b2)-2
=ab[(a+b)2-2ab]-2
=n[22-2n]-2
=4n-2n2-2
=-2n2+4n-2
=-2(n-1)2≤0,
∵-2(n-1)2中只与n有关,故①正确;
根据偶次幂为非负数得:-2(n-1)2≤0,故②正确,③错误;
故选:A.
4.B
【解析】设原来正方形的边长为xcm,增加后边长为(x+2)cm,
根据题意得:(x+2)2-x2=24,
x2+4x+4-x2=24,
4x=20
解得:x=5,
正方形原来的面积是5×5=25cm2.
故选B.
5.A
【解析】解:(m﹣2)(m+2)(m2+4)﹣(m4﹣16)
=(m2﹣4)(m2+4)﹣(m4﹣16)
=(m4﹣16)﹣(m4﹣16)
=0.
故选:A.
6.B
【解析】∵a+b=21,c=15,
∴(a+b)2=441,即a2+b2+2ab=441,
又∵a2+b2=c2=225,
∴2ab=216,
∴ab=54,
即S△ABC=54.
故选B.
7.25
【解析】解:(1),即:,
(2),即:,
故答案为:(1)25;;(2);.
8.-4x-8x+10
【解析】原式=-x+2x-3x-5x-5x+10=-4x-8x+10
故答案为-4x-8x+10
9.3a+1
【解析】解:∵9a2+6a+1=(3a+1)2,
由题可知9a2+6a+1(a>0)是正方形的面积,
∴该正方形的边长是3a+1.
10.2 4
【解析】,
故答案为:,,.
11.
【解析】∵,,
∴=9+4=13,
故答案为:13.
12.; ;
【解析】根据正方形面积公式可得:,正方形面积等于两个小正方形的面积和两个长方形面积之和,即,所以,答案为:, ,.
13.(1);(2);(3);(4).
【解析】解:(1)原式=[(3x 5)+(2x+7)][(3x 5) (2x+7)]
=(3x 5+2x+7)(3x 5 2x 7)
=(5x+2)(x 12)
=;
(2)原式=[(x+y)+1][(x+y) 1]
= 1
=;
(3)原式=
= 6(2x y)+9
=;
(4)原式=
=.
14.49,169
【解析】,,
15.①k=16; ②m=±6.
【解析】①设m2=k;因为a2-8a+k是完全平方式,
所以a2-8a+m2=(a-m)2= a2-2ma+m2,
所以8a=2ma,
解得m=4,
所以k=16;
②因为x2+mx+9是完全平方式,
所以x2+mx+9=(x±3)2,
所以m=±6.
16.(1)(a+b)2=(a﹣b)2+4ab;(2)a﹣b=3.
【解析】(1)根据题意得:
(a+b)2=(a﹣b)2+4ab.
(2)由(1)得(a+b)2=(a﹣b)2+4ab
∴(a﹣b)2=(a+b)2﹣4ab.
当a+b=9,ab=18时,(a﹣b)2=92﹣4×18=9,
∴a﹣b=±
∵a>b
∴a﹣b=3.
17.(1)-7b2+12ab;(2)1700平方米.
【解析】解:(1)(2a+3b)(2a-b)-4(a-b)2=4a2+4ab-3b2-4a2+8ab-4b2=-7b2+12ab;
答:绿化的面积是(-7b2+12ab)平方米;
(2)把a=20,b=10代入-7b2+12ab得,-7×102+12×20×10=1700平方米,
答:绿化面积为1700平方米.
答案第1页,共2页
答案第1页,共2页
