第五章 一元一次方程 同步测试卷 2021-2022学年冀教版七年级数学上册(word版含答案)
文档属性
| 名称 | 第五章 一元一次方程 同步测试卷 2021-2022学年冀教版七年级数学上册(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 94.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-05 21:27:36 | ||
图片预览



文档简介
第五章一元一次方程同步测试卷 2021-2022学年冀教版七年级数学上册
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共10小题,共30分)
下列方程中:-1=x+3;x-1=2:+=13;x-3;x+y=6.其中一元一次方程是( )
A. 个 B. 个 C. 个 D. 个
若a=b,则有下列式子:a-2=b-2;a=b;-a=-b;5a-1=5b-1.正确的有( )
A. 个 B. 个 C. 个 D. 个
下列方程的变形中,正确的是( )
A. 将方程移项,得
B. 将方程两边同除以,得
C. 将方程去括号,得
D. 将方程去分母,得
代数式x-的值等于1时,x的值是( )
A. B. C. D.
若关于x的一元一次方程-=1的解是x=-1,则k的值是( )
A. B. C. D.
粉刷一个房间甲单独做4天完成,乙单独做6天完成,丙单独做12天完成.甲先单独做2天后有事离开,接下来乙、丙共同完成,则乙、丙合作所需要的天数为( )
A. B. C. D.
小明在做解方程作业时,不小心将方程中的一个常数污染了看不清楚,被污染的方程是y-=y-*,怎么办呢 小明想了一想,便翻看了书后的答案,此方程的解是y=-6,小明很快补好了这个常数,并迅速完成了作业,这个常数应是( )
A. B. C. D.
某车间有工人85人,平均每人每天可加工大齿轮16个或小齿轮10个,又知2个大齿轮与3个小齿轮配成一套,若有x人生产大齿轮,则可列方程为( )
A. B.
C. D.
定义“*”运算为“a*b=ab+2a”,若(3*x)+(x*3)=14,则x=( )
A. B. C. D.
我们都知道,无限循环小数都可以转化为分数,例如:将转化为分数时,可设=x,则x=0.6+x,解得x=,即=,仿照这种方法,将化成分数是( )
A. B. C. D.
二、填空题(本大题共6小题,共18分)
方程-=1的解为 .
已知y=3是关于y的方程ay=-6的解,那么关于x的方程4(x-a)=a-(x-6)的解是 .
若(a-2)xa+3+2=0是关于x的一元一次方程,则a= ,方程的解是 .
如图,两根铁棒直立于桶底水平的木桶中,在木桶中加入水后,一根露出水面的长度是它的,另一根露出水面的长度是它的,两根铁棒长度之和为55 cm,此时木桶中水的深度是 .
已知关于x的方程x+3=2x+b的解为x=2,则关于y的一元一次方程-(y-1)+3=-2(y-1)+b的解为 .
有一系列方程,第1个方程是x+=3,解为x=2;第2个方程是+=5,解为x=6;第3个方程是+=7,解为x=12;按此规律:(1)第4个方程是 .(2)第10个方程是 .(3)第n个方程的解是 .
三、计算题(本大题共1小题,共12分)
解下列方程:
(1)5y-3=2y+6;
(2)2(x-2)-3(4x-1)=5(1-x);
(3)-=2-;
(4)-=.
四、解答题(本大题共6小题,共60分)
已知方程(m-3)+4=m-2是关于x的一元一次方程.
(1)求m的值.
(2)写出这个一元一次方程.
已知关于x的两个一元一次方程4x-3m=2的解比4x-2m=x-3的解大2,求m的值.
两地间的路程为360km,甲车从A地出发开往B地,每小时行驶72km;甲车出发25分钟后,乙车从B地出发开往A地,每小时行驶48km,两车相遇后,各自按原来速度继续行驶,直到两车相距100km.则此时甲车从出发开始共行驶了多少小时
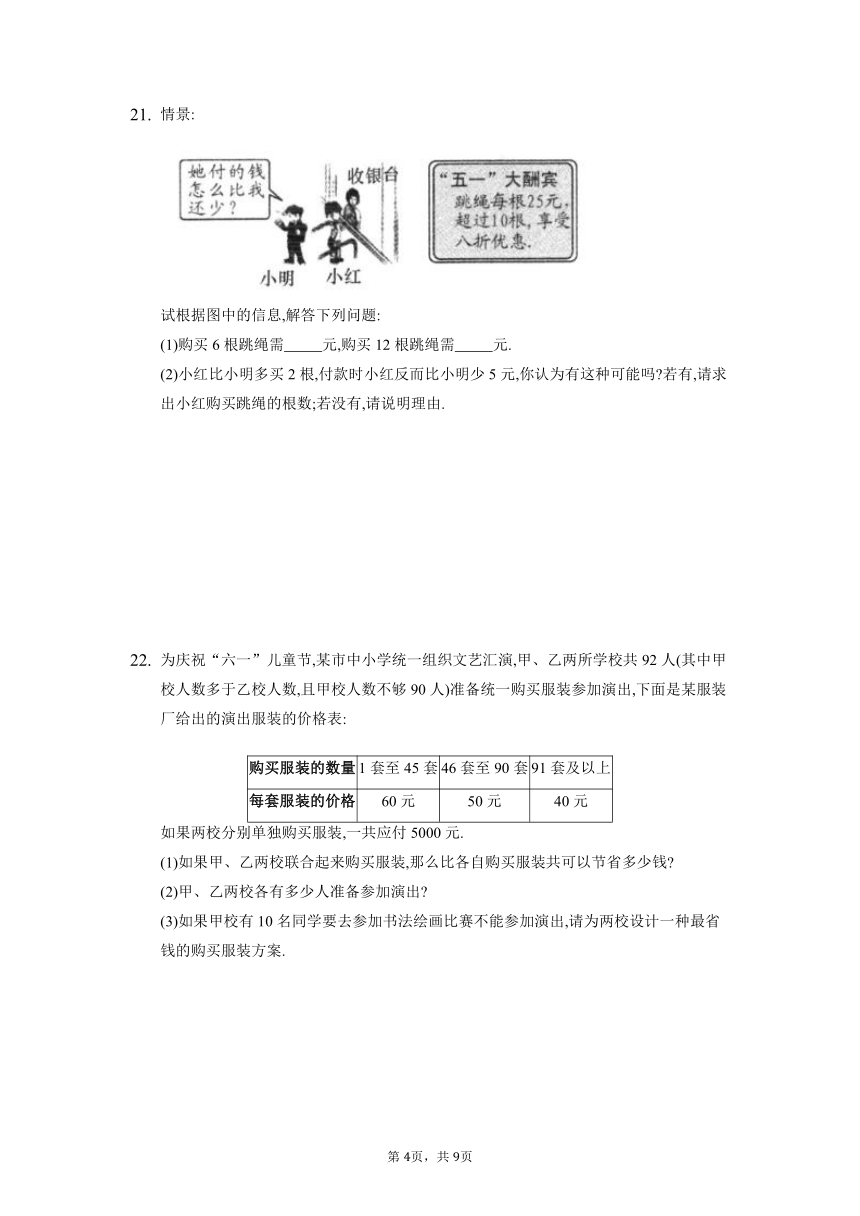
情景:
试根据图中的信息,解答下列问题:
(1)购买6根跳绳需 元,购买12根跳绳需 元.
(2)小红比小明多买2根,付款时小红反而比小明少5元,你认为有这种可能吗 若有,请求出小红购买跳绳的根数;若没有,请说明理由.
为庆祝“六一”儿童节,某市中小学统一组织文艺汇演,甲、乙两所学校共92人(其中甲校人数多于乙校人数,且甲校人数不够90人)准备统一购买服装参加演出,下面是某服装厂给出的演出服装的价格表:
购买服装的数量 1套至45套 46套至90套 91套及以上
每套服装的价格 60元 50元 40元
如果两校分别单独购买服装,一共应付5000元.
(1)如果甲、乙两校联合起来购买服装,那么比各自购买服装共可以节省多少钱
(2)甲、乙两校各有多少人准备参加演出
(3)如果甲校有10名同学要去参加书法绘画比赛不能参加演出,请为两校设计一种最省钱的购买服装方案.
如图,在长方形ABCD中,AB=6cm,BC=12cm,动点M从点A出发,沿线段AB,BC向点C运动,速度为2cm/s;动点N从点B出发,沿射线BC运动,速度为1cm/s,M,N同时运动,当点M到达终点C时,N也停止运动,设运动时间为ts.
(1)请用含t的代数式表示下列线段:当M在AB时,AM= cm,BM= cm,当M在BC上时,BM= cm,MC= cm;BN= cm.
(2)当点M在AB上运动,t为何值时,MB=NB
(3)点M能追上点N吗 若能,求出t的值;若不能,说明理由.
(4)当点M在BC上运动,t为何值时,MN=3cm
1.【答案】A
2.【答案】C
3.【答案】C
4.【答案】B
6.【答案】B
7.【答案】D
8.【答案】C
9.【答案】B
10.【答案】D
11.【答案】m=-18
12.【答案】x=-
13.【答案】-2 x=
14.【答案】20 cm
15.【答案】y=-1
16.【答案】+=9
+=21
n(n+1)
17.【答案】解:(1)移项,得5y-2y=6+3.
合并同类项,得3y=9.
系数化为1,得y=3.
(2)去括号,得2x-4-12x+3=5-5x,
移项,得2x-12x+5x=5+4-3,
合并同类项,得-5x=6,
系数化为1,得x=-.
(3)去分母,得4(7x-1)-6(5x+1)=212-3(3x+2),
去括号,得28x-4-30x-6=24-9x-6,
移项,得28x-30x+9x=24+6+4-6,
合并同类项,得7x=28,
系数化为1,得x=4.
(4)原方程可化为-=.
去分母,得
40x-(16-30x)=2(31x+8).
去括号,得40x-16+30x=62x+16.
移项,得40x+30x-62x=16+16.
合并同类项,得8x=32.
系数化为1,得x=4.
18.【答案】解:(1)由|m|-2=1,
且m-30,
得m=-3.
(2)一元一次方程是-6x+4=-5.
19.【答案】解:由4x-3m=2,得
x=,
由4x-2m=x-3,得
x=.
∵关于x的两个一元一次方程4x-3m=2的解比4x-2m=x-3的解大2,
∴-2=,
解得m=6.
20.【答案】解:甲车共行驶了4h.
21.【答案】解:(1)150;240;
(2)有这种可能.
设小红买了x根跳绳,
则250.8x=25(x-2)-5.
解得x=11.
所以小红买了11根跳绳.
22.【答案】解:(1)由题意得:5000-9240=1320(元)
答:甲、乙两校联合起来购买服装比各自购买服装共可以节省1320元.
(2)设甲校有x人准备参加演出,
则乙校有(92-x)人准备参加演出.
由题意,得
50x+60(92-x)=5000,
解得x=52,
则92-x=40.
答:甲、乙两校分别有52人、40人准备参加演出.
(3)因为甲校有10人不能参加演出,
所以甲校有52-10=42(人)参加演出,
所以两校参加演出的人数为42+40=82(人).
若两校联合购买82套服装,则需要5082=4100(元),
但如果两校联合购买91套服装,
只需4091=3640(元),
3640<4100,
因此,最省钱的购买服装方案是两校联合购买91套服装(即比实际人数多购买9套).
23.【答案】解:(1)2t (6-2 t) (2 t-6) (18-2 t) t
(2)6-2t=t,解得t=2.
所以当点M在AB上运动,t=2s时,MB=NB.
(3)点M能追上点N.
由题意,
得2t-6=t,解得t=6.
所以当点M追上点N时,t=6s.
(4)当BN-BM=MN时,
t-(2t-6)=3,
解得t=3;
当BM- BN=MN时,
2t-6-t=3,
解得t=9.
所以当点M在BC上运动,t=3s或9s时,MN= 3 cm.
第2页,共3页
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共10小题,共30分)
下列方程中:-1=x+3;x-1=2:+=13;x-3;x+y=6.其中一元一次方程是( )
A. 个 B. 个 C. 个 D. 个
若a=b,则有下列式子:a-2=b-2;a=b;-a=-b;5a-1=5b-1.正确的有( )
A. 个 B. 个 C. 个 D. 个
下列方程的变形中,正确的是( )
A. 将方程移项,得
B. 将方程两边同除以,得
C. 将方程去括号,得
D. 将方程去分母,得
代数式x-的值等于1时,x的值是( )
A. B. C. D.
若关于x的一元一次方程-=1的解是x=-1,则k的值是( )
A. B. C. D.
粉刷一个房间甲单独做4天完成,乙单独做6天完成,丙单独做12天完成.甲先单独做2天后有事离开,接下来乙、丙共同完成,则乙、丙合作所需要的天数为( )
A. B. C. D.
小明在做解方程作业时,不小心将方程中的一个常数污染了看不清楚,被污染的方程是y-=y-*,怎么办呢 小明想了一想,便翻看了书后的答案,此方程的解是y=-6,小明很快补好了这个常数,并迅速完成了作业,这个常数应是( )
A. B. C. D.
某车间有工人85人,平均每人每天可加工大齿轮16个或小齿轮10个,又知2个大齿轮与3个小齿轮配成一套,若有x人生产大齿轮,则可列方程为( )
A. B.
C. D.
定义“*”运算为“a*b=ab+2a”,若(3*x)+(x*3)=14,则x=( )
A. B. C. D.
我们都知道,无限循环小数都可以转化为分数,例如:将转化为分数时,可设=x,则x=0.6+x,解得x=,即=,仿照这种方法,将化成分数是( )
A. B. C. D.
二、填空题(本大题共6小题,共18分)
方程-=1的解为 .
已知y=3是关于y的方程ay=-6的解,那么关于x的方程4(x-a)=a-(x-6)的解是 .
若(a-2)xa+3+2=0是关于x的一元一次方程,则a= ,方程的解是 .
如图,两根铁棒直立于桶底水平的木桶中,在木桶中加入水后,一根露出水面的长度是它的,另一根露出水面的长度是它的,两根铁棒长度之和为55 cm,此时木桶中水的深度是 .
已知关于x的方程x+3=2x+b的解为x=2,则关于y的一元一次方程-(y-1)+3=-2(y-1)+b的解为 .
有一系列方程,第1个方程是x+=3,解为x=2;第2个方程是+=5,解为x=6;第3个方程是+=7,解为x=12;按此规律:(1)第4个方程是 .(2)第10个方程是 .(3)第n个方程的解是 .
三、计算题(本大题共1小题,共12分)
解下列方程:
(1)5y-3=2y+6;
(2)2(x-2)-3(4x-1)=5(1-x);
(3)-=2-;
(4)-=.
四、解答题(本大题共6小题,共60分)
已知方程(m-3)+4=m-2是关于x的一元一次方程.
(1)求m的值.
(2)写出这个一元一次方程.
已知关于x的两个一元一次方程4x-3m=2的解比4x-2m=x-3的解大2,求m的值.
两地间的路程为360km,甲车从A地出发开往B地,每小时行驶72km;甲车出发25分钟后,乙车从B地出发开往A地,每小时行驶48km,两车相遇后,各自按原来速度继续行驶,直到两车相距100km.则此时甲车从出发开始共行驶了多少小时
情景:
试根据图中的信息,解答下列问题:
(1)购买6根跳绳需 元,购买12根跳绳需 元.
(2)小红比小明多买2根,付款时小红反而比小明少5元,你认为有这种可能吗 若有,请求出小红购买跳绳的根数;若没有,请说明理由.
为庆祝“六一”儿童节,某市中小学统一组织文艺汇演,甲、乙两所学校共92人(其中甲校人数多于乙校人数,且甲校人数不够90人)准备统一购买服装参加演出,下面是某服装厂给出的演出服装的价格表:
购买服装的数量 1套至45套 46套至90套 91套及以上
每套服装的价格 60元 50元 40元
如果两校分别单独购买服装,一共应付5000元.
(1)如果甲、乙两校联合起来购买服装,那么比各自购买服装共可以节省多少钱
(2)甲、乙两校各有多少人准备参加演出
(3)如果甲校有10名同学要去参加书法绘画比赛不能参加演出,请为两校设计一种最省钱的购买服装方案.
如图,在长方形ABCD中,AB=6cm,BC=12cm,动点M从点A出发,沿线段AB,BC向点C运动,速度为2cm/s;动点N从点B出发,沿射线BC运动,速度为1cm/s,M,N同时运动,当点M到达终点C时,N也停止运动,设运动时间为ts.
(1)请用含t的代数式表示下列线段:当M在AB时,AM= cm,BM= cm,当M在BC上时,BM= cm,MC= cm;BN= cm.
(2)当点M在AB上运动,t为何值时,MB=NB
(3)点M能追上点N吗 若能,求出t的值;若不能,说明理由.
(4)当点M在BC上运动,t为何值时,MN=3cm
1.【答案】A
2.【答案】C
3.【答案】C
4.【答案】B
6.【答案】B
7.【答案】D
8.【答案】C
9.【答案】B
10.【答案】D
11.【答案】m=-18
12.【答案】x=-
13.【答案】-2 x=
14.【答案】20 cm
15.【答案】y=-1
16.【答案】+=9
+=21
n(n+1)
17.【答案】解:(1)移项,得5y-2y=6+3.
合并同类项,得3y=9.
系数化为1,得y=3.
(2)去括号,得2x-4-12x+3=5-5x,
移项,得2x-12x+5x=5+4-3,
合并同类项,得-5x=6,
系数化为1,得x=-.
(3)去分母,得4(7x-1)-6(5x+1)=212-3(3x+2),
去括号,得28x-4-30x-6=24-9x-6,
移项,得28x-30x+9x=24+6+4-6,
合并同类项,得7x=28,
系数化为1,得x=4.
(4)原方程可化为-=.
去分母,得
40x-(16-30x)=2(31x+8).
去括号,得40x-16+30x=62x+16.
移项,得40x+30x-62x=16+16.
合并同类项,得8x=32.
系数化为1,得x=4.
18.【答案】解:(1)由|m|-2=1,
且m-30,
得m=-3.
(2)一元一次方程是-6x+4=-5.
19.【答案】解:由4x-3m=2,得
x=,
由4x-2m=x-3,得
x=.
∵关于x的两个一元一次方程4x-3m=2的解比4x-2m=x-3的解大2,
∴-2=,
解得m=6.
20.【答案】解:甲车共行驶了4h.
21.【答案】解:(1)150;240;
(2)有这种可能.
设小红买了x根跳绳,
则250.8x=25(x-2)-5.
解得x=11.
所以小红买了11根跳绳.
22.【答案】解:(1)由题意得:5000-9240=1320(元)
答:甲、乙两校联合起来购买服装比各自购买服装共可以节省1320元.
(2)设甲校有x人准备参加演出,
则乙校有(92-x)人准备参加演出.
由题意,得
50x+60(92-x)=5000,
解得x=52,
则92-x=40.
答:甲、乙两校分别有52人、40人准备参加演出.
(3)因为甲校有10人不能参加演出,
所以甲校有52-10=42(人)参加演出,
所以两校参加演出的人数为42+40=82(人).
若两校联合购买82套服装,则需要5082=4100(元),
但如果两校联合购买91套服装,
只需4091=3640(元),
3640<4100,
因此,最省钱的购买服装方案是两校联合购买91套服装(即比实际人数多购买9套).
23.【答案】解:(1)2t (6-2 t) (2 t-6) (18-2 t) t
(2)6-2t=t,解得t=2.
所以当点M在AB上运动,t=2s时,MB=NB.
(3)点M能追上点N.
由题意,
得2t-6=t,解得t=6.
所以当点M追上点N时,t=6s.
(4)当BN-BM=MN时,
t-(2t-6)=3,
解得t=3;
当BM- BN=MN时,
2t-6-t=3,
解得t=9.
所以当点M在BC上运动,t=3s或9s时,MN= 3 cm.
第2页,共3页
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
