2.3 弹力(共43张PPT)

(共43张PPT)
第三节　 弹　力
第三节
核心要点突破
课堂互动讲练
课前自主学案
课标定位
课标定位：
应用：1. 分析弹力的方向．
2．利用胡克定律进行简单计算．
理解：1. 弹力产生的条件．
2．胡克定律．
认识：1. 弹性形变的概念及种类．
2．弹力的概念，判断弹力是否存在的方法．
课前自主学案
一、物体的形变
1．形变：物体_____或_______的变化．
2．弹性形变：撤去外力作用后物体___________的形变．
弹性限度：能够完全__________的物体的形变量的最大限度．
3．范性形变：撤去外力后物体的形变或多或少仍有保留而不能_______的形变．
形状
体积
能恢复原状
恢复形状
复原
二、什么是弹力
1．定义：发生弹性形变的物体由于要__________，对与它接触的物体产生的作用力．
2．方向：与引起形变的作用力的方向_______．
3．产生条件：物体间___________且接触处____________．
恢复原状
相反
直接接触
发生形变
思考感悟
相互接触的物体间一定存在弹力作用吗？
提示：弹力产生的条件有两个：相互接触和相互挤压，这两个条件必须同时具备才能产生弹力．因此两个相互接触的物体，如果不能判断它们是否相互挤压，则无法判断它们之间是否一定存在弹力作用．
三、常见的弹力
1．压力和支持力：方向垂直于物体的_______．
2．绳的拉力：方向沿着绳而指向绳_____的方向．
3．弹力的大小：与弹性形变的大小有关，弹性形变越大，弹力也_______，形变消失，弹力随着________．
4．实验探究：弹力与弹簧伸长的关系
接触面
收缩
越大
消失
(1)实验器材：铁架台、弹簧、_____________、钩码若干、坐标纸．
(2)实验过程
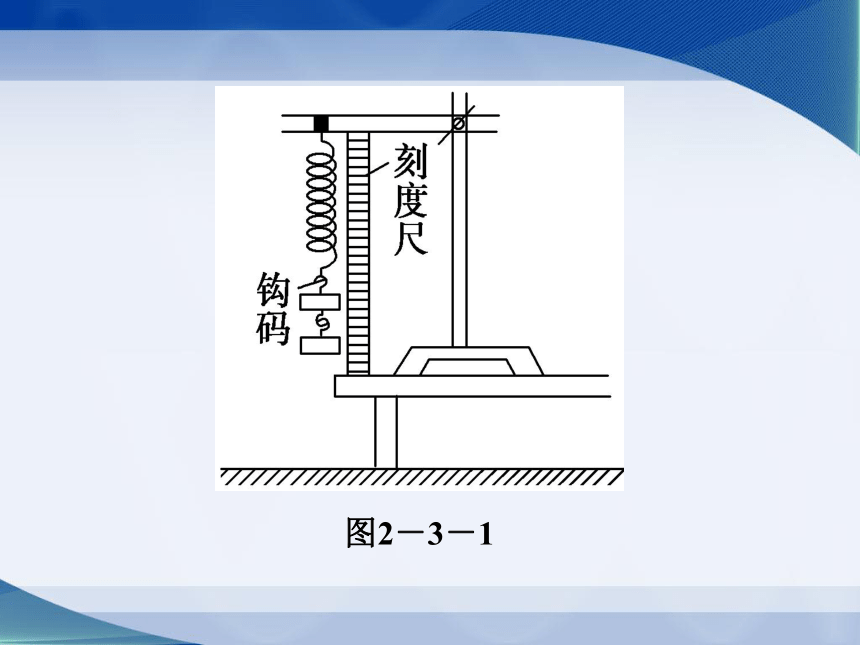
①将弹簧的一端挂在铁架台上，让其自然下垂，用刻度尺测出弹簧自然伸长状态时的长度，即原长．
②如图2－3－1所示，将已知质量的钩码挂在弹簧的下端，在平衡时测出弹簧的总长l并计算钩码的重力F及对应的伸长量x，填写在记录表格里．
毫米刻度尺
图2－3－1
1 2 3 4 5
F/N
l/m
x/m
(l－l0)
③以弹力F(大小等于所挂钩码的重力)为____坐标，以弹簧的伸长量x为____坐标，用描点法作图．连接各点，得出弹力F随弹簧伸长量x变化的图线．
纵
横
④分析图像得出结论．
(3)胡克定律
①内容：在___________内，弹力和弹簧形变大小
(伸长或缩短的量)成_______．
②公式：F＝kx，其中k称为弹簧的___________，单位是牛顿每米，符号是N/m.
弹性限度
正比
劲度系数
核心要点突破
一、弹力是否存在的判断方法
1．根据弹力产生的条件来判断，弹力产生的条件有两个：物体间相互接触并且发生弹性形变，两个条件必须同时满足才有弹力产生．
2．对于形变不明显的情况，可用以下两种方法来判断．
(1)利用假设法判断
可假设在该处把与物体接触的另一物体去掉．看此物体还能否在原位置保持原来的状态，若能保持原来的状态则说明物体间无弹力作用；否则，有弹力作用．
(2)利用力的作用效果分析
如果相互接触的物体间存在弹力，则必有相应的作用效果，或使受力物体发生形变或改变受力物体的运动状态，看物体的受力是否与物体的运动状态相符合，从而确定物体所受弹力的有无．
特别提醒：相互接触是产生弹力的首要条件，但相互接触的物体间不一定存在弹力，只有两个物体接触并产生弹性形变时，两物体间才有弹力产生．
即时应用(即时突破，小试牛刀)
1.下面关于弹力的说法中正确的是(　　)
A．两物体直接接触就一定有弹力作用
B．不直接接触的物体间一定没有弹力作用
C．直接接触的物体之间发生了弹性形变就一定有弹力产生
D．只要物体发生弹性形变就一定有弹力产生
答案：BC
二、弹力方向的确定
弹力的方向与施力物体形变方向相反，作用在受力物体上，几种常见情况如下表：
类型 方向 图示
接触
方式 面与面 垂直公共接触面
点与面 过点垂直于面
点与点 垂直于切面
类型 方向 图示
轻　绳 沿绳收缩方向
轻　杆 可沿杆
可不沿杆
轻弹簧 沿弹簧形变的反方向
特别提醒：判断弹力方向的方法是：先明确两物体之间作用的类型，再根据各种类型的特点来判断弹力的方向．
即时应用(即时突破，小试牛刀)
2.如图2－3－2球A在斜面上，被竖直挡板挡住而处于静止状态，关于球A所受的弹力，以下说法正确的是(　　)
图2－3－2
A．A物体仅受一个弹力作用，弹力的方向垂直斜面向上
B．A物体受两个弹力作用，一个水平向左，一个垂直斜面向下
C．A物体受两个弹力作用，一个水平向右，一个垂直斜面向上
D．A物体受三个弹力作用，一个水平向右，一个垂直斜面向上，一个竖直向下
解析：选C.球A受重力竖直向下，与竖直挡板和斜面都有挤压．斜面给它一个支持力，垂直斜面向上；挡板给它一个支持力，水平向右，故选项C正确．
三、弹力大小的计算
1．弹簧的弹力
(1)应用胡克定律F＝kx求解．
其中x为弹簧的形变量(可能为伸长量，也可能为缩短量)，k为弹簧的劲度系数，只与弹簧本身有关，由弹簧本身的材料、长度、粗细、匝数等因素决定．
(2)弹力与弹簧伸长量的关系可用F－x图像表示，如图2－3－3，图线的斜率即为弹簧的劲度系数．
图2－3－3
(3)弹簧上弹力的变化量ΔF与形变量的变化量也成正比关系，即ΔF＝kΔx.
2．除弹簧这样的弹性体之外的弹力大小的计算，一般要借助物体的运动状态所遵循的物理规律求解．比如悬挂在竖直细绳上的物体处于静止状态时，物体受绳向上的拉力和重力作用．根据二力平衡，可知绳的拉力大小等于物体重力的大小．
即时应用(即时突破，小试牛刀)
3.如图2－3－4所示，一劲度系数为k、原长为l0的轻弹簧，上端固定在天花板上，下端悬挂一个质量为m的小球，小球处于静止状态．弹簧的形变在弹性限度内．已知重力加速度为g.下列判断正确的是(　　)
图2－3－4
课堂互动讲练
弹力有无的判断
判断图2－3－5甲、乙、丙中小球是否受到弹力作用，若受到弹力，请指出其施力物体．
图2－3－5
例1
【思路点拨】　从弹力的产生条件和效果分析．
【精讲精析】　用“消除法”来判断小球是否受斜面的弹力，若将三个图中的斜面去掉，则甲图中小球无法在原位置静止，乙和丙两图中小球仍静止，甲图中小球受到斜面的弹力，施力物体是斜面，同时受细绳的弹力，施力物体是细绳；乙图中小球只受到细绳的弹力，不受斜面的弹力；丙图中小球只受水平面的弹力，不受斜面的弹力．
【答案】　甲图中小球受到绳的拉力和斜面的支持力；乙图中小球受到绳的拉力；丙图中小球受到水平面的支持力．
【方法总结】　在处理弹力问题时，判断接触面间是否挤压(或拉伸)是判断弹力有无的重要方法．一般地，判断接触面间是否存在挤压(或拉伸)的条件，也经常采用“假设法”，即如果物体间有挤压(或拉伸)，则受到某一弹力，当受到这一弹力后物体能否处于当时的状态，如果不能，则此弹力不存在．
变式训练1　在图2－3－6中，A、B两球间一定有弹力作用的是(　　)
图2－3－6
解析：选B.在具体判断有没有挤压时，我们用“拿去法”进行判断，在A中，若拿去A球，则B球静止不动，故A、B间没有挤压，故A、B间没有弹力．在B中，若拿去A球，则B球向左动，故A、B间存在相互挤压，存在弹力．在C中，若拿去A球，则B球静止，故A、B间没有挤压，没有弹力．在D中，若拿去A球及容器壁，则B球向右动，故B对容器右壁有挤压，而对A球没有挤压，A、B间没有弹力．
例2
弹力方向的判断
在图2－3－7所示图中画出物体P受到的各接触点或面对它的弹力的示意图，其中甲、乙、丙中物体P处于静止状态，丁中物体P(即球)在水平面上匀速滚动．
图2－3－7
【思路点拨】　判断弹力方向应把握以下三种情况：
(1)当面(或曲面)接触，弹力垂直于面．
(2)绳上弹力沿绳并指向绳收缩方向．
(3)与球面接触的弹力方向延长线或反向延长线过球心．
【精讲精析】　甲属于绳的拉力，应沿绳指向绳收缩的方向，因此弹力方向沿绳向上；乙中A点属于点与球面相接触，弹力应垂直于球面的切面斜向上，必过球心O，B点属于点与杆相接触，弹力应垂直于球面的切面斜向上；丙中A、B两点都是球面与平面相接触，弹力应垂直于平面，且必过球心，所以A处弹力方向水平向右，B处弹力垂直于斜面向左上方，且都过球心；丁中小球P不管运动与否，都是属于平面与球面相接触，弹力应垂直于平面，且过球心，即竖直向上．
它们所受弹力的示意图如图2－3－8所示．
图2－3－8
【答案】　见精讲精析
如图2－3－9所示，两木块质量分别为m1和m2，两轻质弹簧的劲度系数分别为k1和k2，上面木块压在上面的弹簧上(但不拴接)，整个系统处于平衡状态．试求两弹簧的压缩量x1和x2.
例3
胡克定律的应用
图2－3－9
【思路点拨】　解答此类问题时，应先根据物体的受力情况求出弹簧的弹力，然后再根据胡克定律求出弹簧的形变量．
【方法总结】　(1)本题在求解的过程中用到了二力平衡和“整体法”受力分析的知识，要注意这些知识的灵活应用．
(2)公式F＝kx中，x指的是弹簧的伸缩量，不是弹簧的长度，也不是弹簧长度的变化量．
变式训练2 如图2－3－10所示，A、B是两个相同的弹簧，原长x0＝10 cm，劲度系数k＝500 N/m，如果图中悬挂的两个物体均为m＝1 kg，则两个弹簧的总长度为(　　)
　
图2－3－10
A．22 cm　　　　　　　　B．24 cm
C．26 cm D．28 cm
解析：选C.对下面物体受力分析，由二力平衡得：kxB＝mg，求出xB＝0.02 m＝2 cm，把两个物体看成一个整体，由二力平衡得：kxA＝2mg，求出xA＝0.04 m＝4 cm，所以两个弹簧的总长度为：x0＋xA＋x0＋xB＝26 cm.故只有C项正确.