4.2 共点力平衡条件的应用(共33张PPT)
文档属性
| 名称 | 4.2 共点力平衡条件的应用(共33张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 665.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 教科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-12-04 00:00:00 | ||
图片预览









文档简介
(共33张PPT)
第二节 共点力平衡条件的应用
第二节
核心要点突破
课堂互动讲练
课前自主学案
课标定位
课标定位:
应用:利用平衡条件解决有关物体的平衡问题.
理解:共点力作用下物体的平衡条件.
课前自主学案
一、移动货箱问题
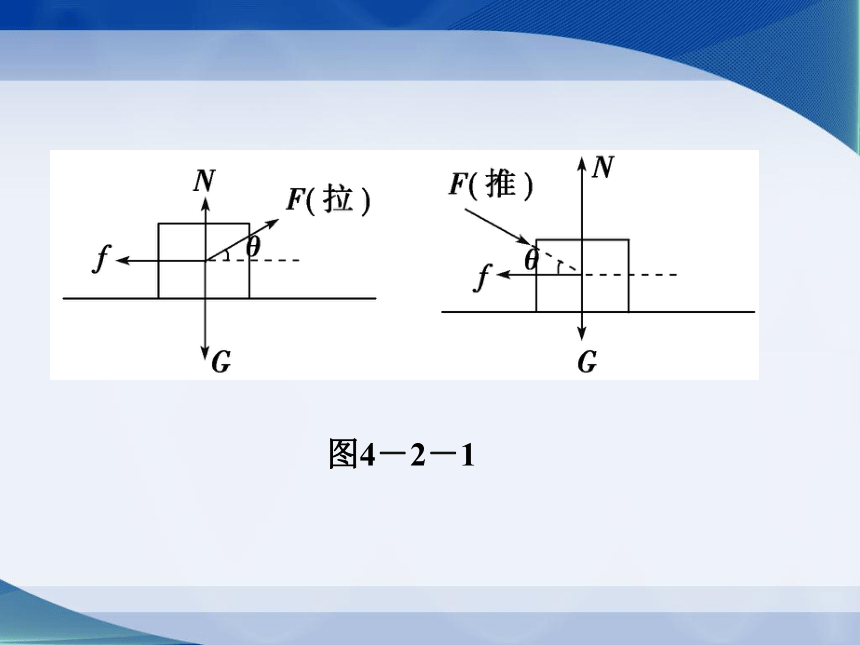
如图4-2-1所示,货箱重力为G,F为它受到的拉(推)力,N为地面支持力,f为摩擦力,货箱受到四个共点力的作用.若它与地面之间的动摩擦因数为μ,则在向前拉的情况下,向前的拉力是_________,地面的支持力是____,摩擦力是_____________,能拉动货箱的条件是______________.在向前推的情况下,向前推的力是________,地面的支持力是____,摩擦力是________,能推动货箱的条件是______________.
Fcosθ
N
μN或f
Fcosθ>μN
Fcosθ
μN或f
Fcosθ>μN
N
图4-2-1
二、绳子粗细的选择
如图4-2-2所示,用绳子把排球网架的直杆垂直于地面拉住三段绳在同一平面内,OA、OB两绳的拉力大小相同,夹角为60°.
图4-2-2 图4-2-3
FAcos30°+FBcos30°
核心要点突破
一、解决平衡问题的常用方法
1.整体法与隔离法:所谓整体法就是对物理问题的整个系统或整个过程进行分析、研究的方法.隔离法是从研究问题的方便性出发,将物体系统中的某一部分隔离出来单独分析研究的方法.
通过整体法分析物理问题,可以弄清系统的整体受力情况和全过程的受力情况,从整体上揭示事物的本质和变化规律,从而避开了中间环节的繁琐推算,能够灵巧地解决问题.
2.相似三角形法:利用表示力的矢量三角形与表示实物的几何三角形相似的关系,建立方程求解,应用这种方法,往往能收到简捷的效果.
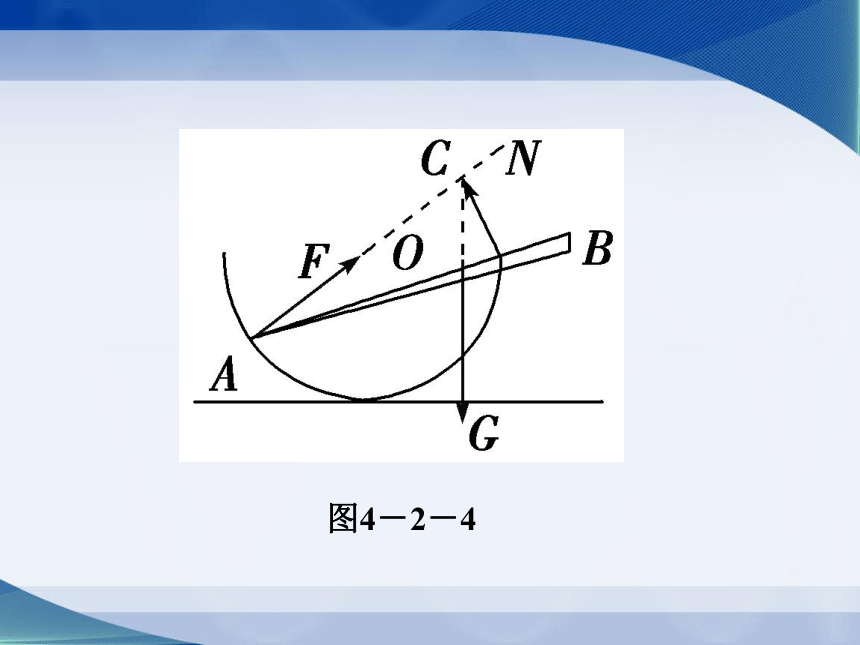
3.三力汇交原理解题法:物体受三个力处于平衡状态,不平行必共点.例如:有一半圆形光滑容器,圆心为O,有一均匀直杆AB如图4-2-4所示放置,若处于平衡状态,则杆所受的重力G、容器对杆的弹力F和N是非平行力,由三力汇交原理可知:G、F、N必相交于一点C.
图4-2-4
即时应用(即时突破,小试牛刀)
1.如图4-2-5所示,物体A、B叠放在水平桌面上,在水平向右的恒力F作用下,A、B正以共同的速度v向右做匀速直线运动,那么关于运动中物体受几个力的说法正确的是( )
图4-2-5
A.A受4个,B受2个
B.A受5个,B受3个
C.A受5个,B受2个
D.A受4个,B受3个
答案:C
二、解决共点力平衡问题的一般步骤
1.选取研究对象
根据题目要求,选取某物体(整体或局部)作为研究对象,在平衡问题中,研究对象常有三种情况:
(1)单个物体.将物体受到的各个力的作用点全都画到物体的几何中心上.
(2)多个物体(系统).在分析外力对系统的作用时,用整体法;在分析系统内各物体间的相互作用时,用隔离法.
(3)几个物体的结点.几根绳、绳和棒之间的结点常常是平衡问题的研究对象.
2.分析研究对象的受力情况,并作出受力图.
3.对研究对象所受的力进行处理,一般情况下利用正交分解法.
4.利用平衡条件建立方程.
5.解方程,必要时对解进行讨论.
特别提醒:(1)解三角形多数情况下是解直角三角形,如果力的三角形并不是直角三角形,能转化为直角三角形的尽量转化为直角三角形.
(2)对于整体法与隔离法一般是结合起来应用,根据题目条件灵活选取先隔离还是先整体,不可将两种方法对立起来.
即时应用(即时突破,小试牛刀)
2.用一轻绳将小球P系于光滑墙壁上的O点,在墙壁和球P之间夹有一矩形物块Q,如图4-2-6所示.P、Q均处于静止状态,则下列相关说法正确的是( )
图4-2- 6
A.P物体受4个力
B.Q受到3个力
C.若绳子变长,绳子的拉力将变小
D.若绳子变短,Q受到的静摩擦力将增大
解析:选AC.因墙壁光滑,故墙壁和Q之间无摩擦力,Q处于平衡状态,一定受重力、P对Q的压力、墙壁对Q的弹力,以及P对Q向上的静摩擦力等4个力作用,而P受重力、绳子的拉力、Q对P的弹力等4个力作用,A项正确,B项错.把P、Q视为一整体,竖直方向有Fcosθ=(mQ+mP)g,其中θ为绳子和墙壁的夹角,易知,绳子变长,拉力变小,P、Q之间的静摩擦力不变,C项正确,D项错.
课堂互动讲练
整体法和隔离法处理平衡问题
如图4-2-7所示,一根细绳上吊着A、B两个小球,当两个大小相等、方向相反的水平力分别作用在两个小球上时,可能形成图所示的哪种情况( )
例1
图4-2-7
图4-2-8
【思路点拨】 先以整体为研究对象判断上端悬线的位置情况,再以B球作为研究对象判断中间悬线的位置情况,不论是整体还是其中的一部分都应满足平衡条件.
【自主解答】 把A、B作为一个整体来研究,受到的水平方向的力等大、反向,故合力为零,因此A球上端的悬线应竖直;研究B球,受到水平向右的力,因此B球上端的悬线必偏离竖直方向向右.
【答案】 B
【方法总结】 当一个系统处于平衡状态时,组成系统的每一个物体都处于平衡状态.一般地,当求系统内各部分间的相互作用时用隔离法;求系统受到的外力作用时用整体法.整体法的优点是研究对象少,未知量少,方程数少,求解较简捷.在实际应用中往往将二者结合应用.
变式训练1 如图4-2-9所示,质量为M的楔形物块静置在水平地面上,其斜面的倾角为θ.斜面上有一质量为m的小物块,小物块与斜面之间存在摩擦.用恒力F沿斜面向上拉小物块,物块和楔形物块始终保持静止,则地面对楔形物块的支持力为( )
图4-2-9
A.(M+m)g
B.(M+m)g-F
C.(M+m)g+Fsinθ
D.(M+m)g-Fsinθ
解析:选D.F的分解情况如图所示,将M、m视为一个系统,F的作用产生两个效果:一是使系统相对地面有向左运动的趋势,相当于分力F1的作用;二是将系统向上提起,相当于分力F2的作用,F2=Fsinθ.地面对楔形物块的支持力N=(M+m)g-Fsinθ,故D正确.
例2
共点力的动态平衡问题
(2011年高考安徽卷)一质量为m的物块恰好静止在倾角为θ的斜面上,现对物块施加一个竖直向下的恒力F,如图4-2-10所示.则物块
( )
A.仍处于静止状态
B.沿斜面加速下滑
C.受到的摩擦力不变
D.受到的合外力增大
图4-2-10
【思路点拨】 物体不加力F时的受力情况,“恰好静止”物体所受静摩擦力等于滑动摩擦力,可求出摩擦因数,加力F后再进行受力分析,判断运动状态.
【精讲精析】 无力F时受力情况如图4-2-11甲,使物体下滑的力F1=mgsinθ,物体受到最大静摩擦力fmax=μN=μmgcosθ,“物体恰好静止”受最大静摩擦力可认为等于滑动摩擦力,mgsinθ=μmgcosθ,μ=tanθ;当施加恒力F后,受力情况如图乙,
图4-2-11
使物体下滑的力为:F2=mgsinθ+Fsinθ,物体所受最大静摩擦力为:f′max=μ(mgcosθ+Fcosθ)=mgsinθ+Fsinθ,即F2=f′max,两者相等,物体仍处于静止状态.A正确,B错误;由于f′max>fmax,故C错误;物体始终静止,则受到的合力始终为零,D错误.
【答案】 A
变式训练2 放在水平地面上的物块,受到一个与水平面方向成θ角斜向下的力F的作用,物块在水平地面上做匀速直线运动,如图4-2-12所示,如果保持力F的大小不变,而使力F与水平方向的夹角θ减小,那么地面受到的压力N和物块受到的摩擦力f的变化情况是( )
A.N变小,f变大
B.N变大,f变大
C.N变小,f变小
D.N变大,f变小
图4-2-12
解析:选C.对物体受力分析如图所示,物体在竖直方向上合力为零可得:N=mg+Fsinθ,N随θ的减小而减小,f为滑动摩擦力,f=μN,可见f随N的减小而减小,只有C正确.
第二节 共点力平衡条件的应用
第二节
核心要点突破
课堂互动讲练
课前自主学案
课标定位
课标定位:
应用:利用平衡条件解决有关物体的平衡问题.
理解:共点力作用下物体的平衡条件.
课前自主学案
一、移动货箱问题
如图4-2-1所示,货箱重力为G,F为它受到的拉(推)力,N为地面支持力,f为摩擦力,货箱受到四个共点力的作用.若它与地面之间的动摩擦因数为μ,则在向前拉的情况下,向前的拉力是_________,地面的支持力是____,摩擦力是_____________,能拉动货箱的条件是______________.在向前推的情况下,向前推的力是________,地面的支持力是____,摩擦力是________,能推动货箱的条件是______________.
Fcosθ
N
μN或f
Fcosθ>μN
Fcosθ
μN或f
Fcosθ>μN
N
图4-2-1
二、绳子粗细的选择
如图4-2-2所示,用绳子把排球网架的直杆垂直于地面拉住三段绳在同一平面内,OA、OB两绳的拉力大小相同,夹角为60°.
图4-2-2 图4-2-3
FAcos30°+FBcos30°
核心要点突破
一、解决平衡问题的常用方法
1.整体法与隔离法:所谓整体法就是对物理问题的整个系统或整个过程进行分析、研究的方法.隔离法是从研究问题的方便性出发,将物体系统中的某一部分隔离出来单独分析研究的方法.
通过整体法分析物理问题,可以弄清系统的整体受力情况和全过程的受力情况,从整体上揭示事物的本质和变化规律,从而避开了中间环节的繁琐推算,能够灵巧地解决问题.
2.相似三角形法:利用表示力的矢量三角形与表示实物的几何三角形相似的关系,建立方程求解,应用这种方法,往往能收到简捷的效果.
3.三力汇交原理解题法:物体受三个力处于平衡状态,不平行必共点.例如:有一半圆形光滑容器,圆心为O,有一均匀直杆AB如图4-2-4所示放置,若处于平衡状态,则杆所受的重力G、容器对杆的弹力F和N是非平行力,由三力汇交原理可知:G、F、N必相交于一点C.
图4-2-4
即时应用(即时突破,小试牛刀)
1.如图4-2-5所示,物体A、B叠放在水平桌面上,在水平向右的恒力F作用下,A、B正以共同的速度v向右做匀速直线运动,那么关于运动中物体受几个力的说法正确的是( )
图4-2-5
A.A受4个,B受2个
B.A受5个,B受3个
C.A受5个,B受2个
D.A受4个,B受3个
答案:C
二、解决共点力平衡问题的一般步骤
1.选取研究对象
根据题目要求,选取某物体(整体或局部)作为研究对象,在平衡问题中,研究对象常有三种情况:
(1)单个物体.将物体受到的各个力的作用点全都画到物体的几何中心上.
(2)多个物体(系统).在分析外力对系统的作用时,用整体法;在分析系统内各物体间的相互作用时,用隔离法.
(3)几个物体的结点.几根绳、绳和棒之间的结点常常是平衡问题的研究对象.
2.分析研究对象的受力情况,并作出受力图.
3.对研究对象所受的力进行处理,一般情况下利用正交分解法.
4.利用平衡条件建立方程.
5.解方程,必要时对解进行讨论.
特别提醒:(1)解三角形多数情况下是解直角三角形,如果力的三角形并不是直角三角形,能转化为直角三角形的尽量转化为直角三角形.
(2)对于整体法与隔离法一般是结合起来应用,根据题目条件灵活选取先隔离还是先整体,不可将两种方法对立起来.
即时应用(即时突破,小试牛刀)
2.用一轻绳将小球P系于光滑墙壁上的O点,在墙壁和球P之间夹有一矩形物块Q,如图4-2-6所示.P、Q均处于静止状态,则下列相关说法正确的是( )
图4-2- 6
A.P物体受4个力
B.Q受到3个力
C.若绳子变长,绳子的拉力将变小
D.若绳子变短,Q受到的静摩擦力将增大
解析:选AC.因墙壁光滑,故墙壁和Q之间无摩擦力,Q处于平衡状态,一定受重力、P对Q的压力、墙壁对Q的弹力,以及P对Q向上的静摩擦力等4个力作用,而P受重力、绳子的拉力、Q对P的弹力等4个力作用,A项正确,B项错.把P、Q视为一整体,竖直方向有Fcosθ=(mQ+mP)g,其中θ为绳子和墙壁的夹角,易知,绳子变长,拉力变小,P、Q之间的静摩擦力不变,C项正确,D项错.
课堂互动讲练
整体法和隔离法处理平衡问题
如图4-2-7所示,一根细绳上吊着A、B两个小球,当两个大小相等、方向相反的水平力分别作用在两个小球上时,可能形成图所示的哪种情况( )
例1
图4-2-7
图4-2-8
【思路点拨】 先以整体为研究对象判断上端悬线的位置情况,再以B球作为研究对象判断中间悬线的位置情况,不论是整体还是其中的一部分都应满足平衡条件.
【自主解答】 把A、B作为一个整体来研究,受到的水平方向的力等大、反向,故合力为零,因此A球上端的悬线应竖直;研究B球,受到水平向右的力,因此B球上端的悬线必偏离竖直方向向右.
【答案】 B
【方法总结】 当一个系统处于平衡状态时,组成系统的每一个物体都处于平衡状态.一般地,当求系统内各部分间的相互作用时用隔离法;求系统受到的外力作用时用整体法.整体法的优点是研究对象少,未知量少,方程数少,求解较简捷.在实际应用中往往将二者结合应用.
变式训练1 如图4-2-9所示,质量为M的楔形物块静置在水平地面上,其斜面的倾角为θ.斜面上有一质量为m的小物块,小物块与斜面之间存在摩擦.用恒力F沿斜面向上拉小物块,物块和楔形物块始终保持静止,则地面对楔形物块的支持力为( )
图4-2-9
A.(M+m)g
B.(M+m)g-F
C.(M+m)g+Fsinθ
D.(M+m)g-Fsinθ
解析:选D.F的分解情况如图所示,将M、m视为一个系统,F的作用产生两个效果:一是使系统相对地面有向左运动的趋势,相当于分力F1的作用;二是将系统向上提起,相当于分力F2的作用,F2=Fsinθ.地面对楔形物块的支持力N=(M+m)g-Fsinθ,故D正确.
例2
共点力的动态平衡问题
(2011年高考安徽卷)一质量为m的物块恰好静止在倾角为θ的斜面上,现对物块施加一个竖直向下的恒力F,如图4-2-10所示.则物块
( )
A.仍处于静止状态
B.沿斜面加速下滑
C.受到的摩擦力不变
D.受到的合外力增大
图4-2-10
【思路点拨】 物体不加力F时的受力情况,“恰好静止”物体所受静摩擦力等于滑动摩擦力,可求出摩擦因数,加力F后再进行受力分析,判断运动状态.
【精讲精析】 无力F时受力情况如图4-2-11甲,使物体下滑的力F1=mgsinθ,物体受到最大静摩擦力fmax=μN=μmgcosθ,“物体恰好静止”受最大静摩擦力可认为等于滑动摩擦力,mgsinθ=μmgcosθ,μ=tanθ;当施加恒力F后,受力情况如图乙,
图4-2-11
使物体下滑的力为:F2=mgsinθ+Fsinθ,物体所受最大静摩擦力为:f′max=μ(mgcosθ+Fcosθ)=mgsinθ+Fsinθ,即F2=f′max,两者相等,物体仍处于静止状态.A正确,B错误;由于f′max>fmax,故C错误;物体始终静止,则受到的合力始终为零,D错误.
【答案】 A
变式训练2 放在水平地面上的物块,受到一个与水平面方向成θ角斜向下的力F的作用,物块在水平地面上做匀速直线运动,如图4-2-12所示,如果保持力F的大小不变,而使力F与水平方向的夹角θ减小,那么地面受到的压力N和物块受到的摩擦力f的变化情况是( )
A.N变小,f变大
B.N变大,f变大
C.N变小,f变小
D.N变大,f变小
图4-2-12
解析:选C.对物体受力分析如图所示,物体在竖直方向上合力为零可得:N=mg+Fsinθ,N随θ的减小而减小,f为滑动摩擦力,f=μN,可见f随N的减小而减小,只有C正确.
同课章节目录
- 第一章 运动的描述
- 1 质点 参考系 空间 时间
- 2 位置变化的描述——位移
- 3 运动快慢与方向的描述——速度
- 4 速度变化快慢的描述——加速度
- 5 匀变速直线运动速度与时间的关系
- 6 匀变速直线运动位移与时间的关系
- 7 对自由落体运动的研究
- 8 匀变速直线运动规律的应用
- 9 测定匀变速直线运动的加速度
- 第二章 力
- 1 力
- 2 重力
- 3 弹力
- 4 摩擦力
- 5 力的合成
- 6 力的分解
- 第三章 牛顿运动定律
- 1 牛顿第一定律
- 2 探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 牛顿第三定律
- 5 牛顿运动定律的应用
- 6 超重与失重
- 第四章 物体的平衡
- 1 共点力作用下物体的平衡
- 2 共点力平衡条件的应用
- 3 平衡的稳定性(选学)
