人教版数学九上24.1.1圆(共40张PPT)
文档属性
| 名称 | 人教版数学九上24.1.1圆(共40张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 8.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-05 00:00:00 | ||
图片预览











文档简介
(共40张PPT)
圆
圆是一种基本的几何图形,圆形物体在生活中随处可见
圆是一种基本的几何图形,圆形物体在生活中随处可见
圆的历史
古代人最早是从太阳,阴历十五的月亮得到圆的概念的.
那么是什么人做出第一个圆的呢?
圆的历史
18 000 年前的山顶洞人用一种尖状的石器来钻孔,一面钻不透,再从另一面钻,石器的尖是圆心,它的宽度的一半就是半径,这样以同一个半径和圆心一圈圈地转,就可以钻出一个圆的孔.
到了陶器时代,许多陶器都是圆的,
圆的陶器是将泥土放在一个转盘上制成的.
圆的历史
圆的历史
我国古代,半坡人就已经会造圆形的房顶了.
圆的历史
大约在同一时代,美索不达米亚人做出了
世界上第一个轮子——圆的木轮。
圆的历史
很早之前,人们将圆的木轮固定在木架上,
这样就成了最初的车子.
圆的历史
2 000 多年前,墨子给出圆的定义“一中同长也”,
意思是说,圆有一个圆心,圆心到圆周的长都相等.
这个定义比古希腊数学家欧几里得给圆下的定义要早很多年.
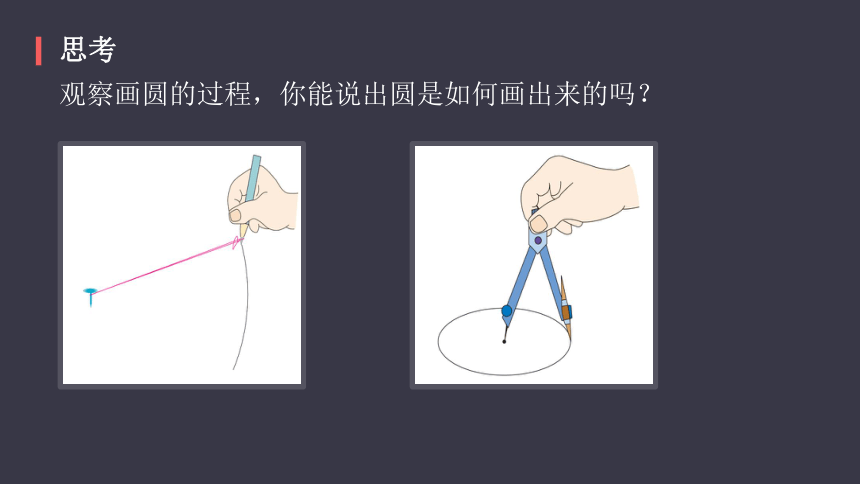
观察画圆的过程,你能说出圆是如何画出来的吗?
思考
如图,在一个平面内,线段 OA 绕它固定的一个端点O旋转一周,另一个端点 A 所形成的图形叫做圆.
圆的定义
固定的端点O,叫做圆心.
线段OA,叫做半径.
以点O为圆心的圆,记作“⊙O”,读作“圆O”.
战国时期的《墨经》就有“圆,一中同长也”的记载。
它的意思是圆上各点到圆心的距离都等于半径.
O
A
r
①“圆”指的是“圆周”,即一条封闭曲线.
注意事项
②确定圆的两要素:圆心和半径.
圆心定_____,半径定_____.
位置
大小
从画圆的过程可以看出:
思考
圆上各点到定点(圆心O)的距离都等于定长(半径r).
那反过来,到定点距离等于定长的点是否都在同一个圆上呢?
O
A
r
归纳
集合的观点
圆心为O、半径为r 的圆可以看成是到定点O 的距离等于定长r 的所有点组成的图形(集合).
运动的观点
在一个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点A所形成的图形叫做圆.
画一画
已知AB=3cm,作图说明满足下列要求的图形:
(1)到点A的距离等于2cm的所有点组成的图形.
(2)到点B的距离等于2cm的所有点组成的图形.
(3)到点A和B的距离都等于2cm的所有点组成的图形.
为什么车轮要做成圆形的呢?
思考
为什么车轮要做成圆形的呢?
思考
为什么车轮要做成圆形的呢?
思考
把车轮做成圆形,车轮上各点到车轮中心(圆心)的距离都等于车轮的半径,当车轮在平面上滚动时,车轮中心与平面的距离保持不变,
因此,当车辆在平坦的路上行驶时,坐车的人会感觉到非常平稳,
这也是车轮都做成圆形的数学道理.
为什么车轮要做成圆形的呢?
例题
A
B
C
D
O
矩形ABCD的对角线AC,BD相交于点O.
求证:A,B,C,D四个点在以O为圆心的同一个圆上.
证明:
∵四边形ABCD为矩形,
∴OA=OC=OB=OD.
∴A,B,C,D四个点在以点O为圆心,OA为半径的圆上.
弦
连接圆上任意两点的线段(如图AC),叫做弦.
经过圆心的弦(如图中的AB),叫做直径.
O
A
B
C
圆中的弦有没有最大值呢?
探究
小明和小强为了探究圆O 中有没有最长的弦,经过了大量的测量,最后得出一致结论,直径是圆中最长的弦,你认为他们的结论对吗?试说说你的理由.
如图,已知AB是圆O 的直径,CD是不过圆心的弦.求证:AB>CD.
证明:连接OC,OD,
由三角形的三边关系可知
OC+ OD>CD
∵ OC=OD=OA=OB
∴ OC+OD=AB
∴ AB>CD
A
B
C
D
O
弧
圆上任意两点间的部分叫做圆弧,简称弧.
圆的任意一条直径的两个端点把圆分成两条弧,
每一条弧都叫做半圆.
O
A
B
C
以A,B为端点的弧记作
,读作“圆弧AB”或“弧AB”.
小于半圆的弧(如图中的
优弧和劣弧
大于半圆的弧(用三个字母表示,如图中的
O
A
B
C
),叫做劣弧.
),叫做优弧.
能够重合的两个圆,叫做等圆.
等圆和等弧
在同圆或等圆中,能够互相重合的弧,叫做等弧.
判断下列说法的对错
等圆的半径相等
等弧的长度相等
半径相等的圆是等圆
长度相等的弧是等弧
长度相等不一定能重合
如图,半径有:_______________
若∠AOB=60°,
则△AOB是______三角形.
练习
OA,OB,OC
等边
A
B
C
O
A
B
C
O
练习
如图,劣弧有:__________
如图,优弧有:______________
还有其他弧吗?
还有半圆
如图,请正确的方式表示出以点A为端点的优弧及劣弧.
练习
优弧
劣弧
练习
1
3
4
4
如图,圆中有________条直径,_________条弦,圆中以 A 为一个端点的优弧有__________条,劣弧有_________条 .
练习——概念辨析
D
半径为 5 的圆的一条弦长不可能是 ( )
A.3
B.5
C.10
D.12
练习——概念辨析
判断下列说法的正误:
(1)弦是直径;( )
(2)半圆是弧; ( )
(3)过圆心的线段是直径; ( )
(4)过圆心的直线是直径;( )
(5)半圆是最长的弧;( )
(6)直径是最长的弦;( )
(7)圆心相同,半径相等的两个圆是同心圆;( )
(8)半径相等的两个圆是等圆.( )
练习——概念辨析
下列说法正确的是( )
A.长度相等的两条弧是等弧
B.优弧一定大于劣弧
C.不同的圆中不可能有相等的弦
D.直径是弦且是同一个圆中最长的弦
D
练习——概念辨析
下列说法:
① 优弧一定比劣弧长 ;
② 面积相等的两个圆是等圆 ;
③ 长度相等的弧是等弧;
④ 经过圆内的一个定点可以作无数条弦;
⑤ 经过圆内一定点可以作无数条直径 .
其中不正确的有_______个.
3
1.如何在操场上画一个半径是5m的圆?说出你的理由.
练习
2.你见过树木的年轮吗 从树木的年轮,可以很清楚的看出树木生长的年龄,如果一棵20年树龄的红杉树的树干直径是23cm,这棵红杉树的半径每年增加多少
练习
练习
3.△ABC中,∠C=90°.求证:A,B,C三点在同一个圆上.
如图,一根5m长的绳子,一端栓在柱子上,另一端栓着一只羊,请画出羊的活动区域.
小羊的活动范围
这节课我们学会了什么?
总结
1.圆的定义:
在一个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点A所形成的图形叫做圆.
2.确定圆的两要素:圆心和半径.
O
A
r
圆心定_____,半径定_____.
位置
大小
这节课我们学会了什么?
总结
3.弦和弧的相关概念:
圆上任意两点间的部分叫做圆弧,简称弧.
连接圆上任意两点的线段(如图AC),叫做弦.
经过圆心的弦(如图中的AB),叫做直径.
O
A
B
C
小于半圆的弧(如图中的
大于半圆的弧(用三个字母表示,如图中的
),叫做劣弧.
),
叫做优弧.
圆
圆是一种基本的几何图形,圆形物体在生活中随处可见
圆是一种基本的几何图形,圆形物体在生活中随处可见
圆的历史
古代人最早是从太阳,阴历十五的月亮得到圆的概念的.
那么是什么人做出第一个圆的呢?
圆的历史
18 000 年前的山顶洞人用一种尖状的石器来钻孔,一面钻不透,再从另一面钻,石器的尖是圆心,它的宽度的一半就是半径,这样以同一个半径和圆心一圈圈地转,就可以钻出一个圆的孔.
到了陶器时代,许多陶器都是圆的,
圆的陶器是将泥土放在一个转盘上制成的.
圆的历史
圆的历史
我国古代,半坡人就已经会造圆形的房顶了.
圆的历史
大约在同一时代,美索不达米亚人做出了
世界上第一个轮子——圆的木轮。
圆的历史
很早之前,人们将圆的木轮固定在木架上,
这样就成了最初的车子.
圆的历史
2 000 多年前,墨子给出圆的定义“一中同长也”,
意思是说,圆有一个圆心,圆心到圆周的长都相等.
这个定义比古希腊数学家欧几里得给圆下的定义要早很多年.
观察画圆的过程,你能说出圆是如何画出来的吗?
思考
如图,在一个平面内,线段 OA 绕它固定的一个端点O旋转一周,另一个端点 A 所形成的图形叫做圆.
圆的定义
固定的端点O,叫做圆心.
线段OA,叫做半径.
以点O为圆心的圆,记作“⊙O”,读作“圆O”.
战国时期的《墨经》就有“圆,一中同长也”的记载。
它的意思是圆上各点到圆心的距离都等于半径.
O
A
r
①“圆”指的是“圆周”,即一条封闭曲线.
注意事项
②确定圆的两要素:圆心和半径.
圆心定_____,半径定_____.
位置
大小
从画圆的过程可以看出:
思考
圆上各点到定点(圆心O)的距离都等于定长(半径r).
那反过来,到定点距离等于定长的点是否都在同一个圆上呢?
O
A
r
归纳
集合的观点
圆心为O、半径为r 的圆可以看成是到定点O 的距离等于定长r 的所有点组成的图形(集合).
运动的观点
在一个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点A所形成的图形叫做圆.
画一画
已知AB=3cm,作图说明满足下列要求的图形:
(1)到点A的距离等于2cm的所有点组成的图形.
(2)到点B的距离等于2cm的所有点组成的图形.
(3)到点A和B的距离都等于2cm的所有点组成的图形.
为什么车轮要做成圆形的呢?
思考
为什么车轮要做成圆形的呢?
思考
为什么车轮要做成圆形的呢?
思考
把车轮做成圆形,车轮上各点到车轮中心(圆心)的距离都等于车轮的半径,当车轮在平面上滚动时,车轮中心与平面的距离保持不变,
因此,当车辆在平坦的路上行驶时,坐车的人会感觉到非常平稳,
这也是车轮都做成圆形的数学道理.
为什么车轮要做成圆形的呢?
例题
A
B
C
D
O
矩形ABCD的对角线AC,BD相交于点O.
求证:A,B,C,D四个点在以O为圆心的同一个圆上.
证明:
∵四边形ABCD为矩形,
∴OA=OC=OB=OD.
∴A,B,C,D四个点在以点O为圆心,OA为半径的圆上.
弦
连接圆上任意两点的线段(如图AC),叫做弦.
经过圆心的弦(如图中的AB),叫做直径.
O
A
B
C
圆中的弦有没有最大值呢?
探究
小明和小强为了探究圆O 中有没有最长的弦,经过了大量的测量,最后得出一致结论,直径是圆中最长的弦,你认为他们的结论对吗?试说说你的理由.
如图,已知AB是圆O 的直径,CD是不过圆心的弦.求证:AB>CD.
证明:连接OC,OD,
由三角形的三边关系可知
OC+ OD>CD
∵ OC=OD=OA=OB
∴ OC+OD=AB
∴ AB>CD
A
B
C
D
O
弧
圆上任意两点间的部分叫做圆弧,简称弧.
圆的任意一条直径的两个端点把圆分成两条弧,
每一条弧都叫做半圆.
O
A
B
C
以A,B为端点的弧记作
,读作“圆弧AB”或“弧AB”.
小于半圆的弧(如图中的
优弧和劣弧
大于半圆的弧(用三个字母表示,如图中的
O
A
B
C
),叫做劣弧.
),叫做优弧.
能够重合的两个圆,叫做等圆.
等圆和等弧
在同圆或等圆中,能够互相重合的弧,叫做等弧.
判断下列说法的对错
等圆的半径相等
等弧的长度相等
半径相等的圆是等圆
长度相等的弧是等弧
长度相等不一定能重合
如图,半径有:_______________
若∠AOB=60°,
则△AOB是______三角形.
练习
OA,OB,OC
等边
A
B
C
O
A
B
C
O
练习
如图,劣弧有:__________
如图,优弧有:______________
还有其他弧吗?
还有半圆
如图,请正确的方式表示出以点A为端点的优弧及劣弧.
练习
优弧
劣弧
练习
1
3
4
4
如图,圆中有________条直径,_________条弦,圆中以 A 为一个端点的优弧有__________条,劣弧有_________条 .
练习——概念辨析
D
半径为 5 的圆的一条弦长不可能是 ( )
A.3
B.5
C.10
D.12
练习——概念辨析
判断下列说法的正误:
(1)弦是直径;( )
(2)半圆是弧; ( )
(3)过圆心的线段是直径; ( )
(4)过圆心的直线是直径;( )
(5)半圆是最长的弧;( )
(6)直径是最长的弦;( )
(7)圆心相同,半径相等的两个圆是同心圆;( )
(8)半径相等的两个圆是等圆.( )
练习——概念辨析
下列说法正确的是( )
A.长度相等的两条弧是等弧
B.优弧一定大于劣弧
C.不同的圆中不可能有相等的弦
D.直径是弦且是同一个圆中最长的弦
D
练习——概念辨析
下列说法:
① 优弧一定比劣弧长 ;
② 面积相等的两个圆是等圆 ;
③ 长度相等的弧是等弧;
④ 经过圆内的一个定点可以作无数条弦;
⑤ 经过圆内一定点可以作无数条直径 .
其中不正确的有_______个.
3
1.如何在操场上画一个半径是5m的圆?说出你的理由.
练习
2.你见过树木的年轮吗 从树木的年轮,可以很清楚的看出树木生长的年龄,如果一棵20年树龄的红杉树的树干直径是23cm,这棵红杉树的半径每年增加多少
练习
练习
3.△ABC中,∠C=90°.求证:A,B,C三点在同一个圆上.
如图,一根5m长的绳子,一端栓在柱子上,另一端栓着一只羊,请画出羊的活动区域.
小羊的活动范围
这节课我们学会了什么?
总结
1.圆的定义:
在一个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点A所形成的图形叫做圆.
2.确定圆的两要素:圆心和半径.
O
A
r
圆心定_____,半径定_____.
位置
大小
这节课我们学会了什么?
总结
3.弦和弧的相关概念:
圆上任意两点间的部分叫做圆弧,简称弧.
连接圆上任意两点的线段(如图AC),叫做弦.
经过圆心的弦(如图中的AB),叫做直径.
O
A
B
C
小于半圆的弧(如图中的
大于半圆的弧(用三个字母表示,如图中的
),叫做劣弧.
),
叫做优弧.
同课章节目录
