华师大版七年级数学上册2.6.1有理数的加法课件(共25张PPT)
文档属性
| 名称 | 华师大版七年级数学上册2.6.1有理数的加法课件(共25张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 825.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-05 15:32:11 | ||
图片预览







文档简介
(共25张PPT)
华东师范大学出版社
一、引入课题
同学们,现已金秋,秋高气爽,据网上气温资料显示,昨天早晨8点我们这里的气温是20℃,到了午后的13点气温上升了5℃,但是到了下午的17点气温又下降了4℃,你能知道13点和17点的气温各是多少吗?
二、学习目标
1.理解有理数加法法则的意义,掌握有理数的加法法则。
2. 能运用有理数的加法法则进行有理数的加法运算。??
重点、难点
1.重点:有理数加法法则。
2.难点:异号两数相加的法则 。
三、新知探究
问题:
小明在一条东西方向的直道上,先走了20米,又走了30米,能否确定他现在位于原来位置的哪个方向,与原来位置相距多少米?
(1)若两次都是向东走
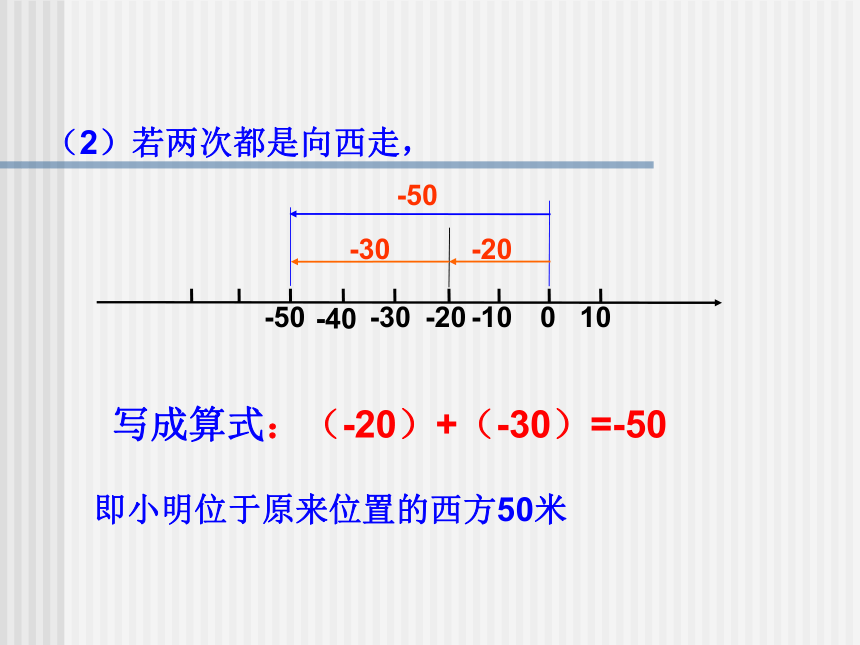
(2)若两次都是向西走
(3)若第一次向东走20米,第二次向西走了30米
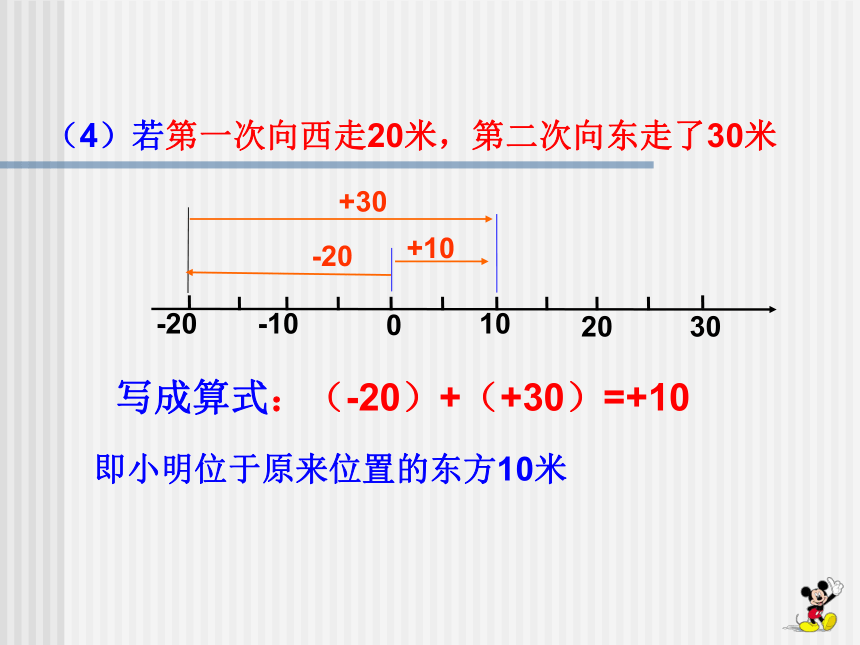
(4)若第一次向西走20米,第二次向东走了30米
试验:
因为这个问题涉及到方向,不妨规定向东为正,向西为负。
(1)若两次都是向东走,
10
30
40
+30
50
-10
0
20
+20
+50
即小明位于原来位置的东方50米
写成算式:(+20)+(+30)=+50
(2)若两次都是向西走,
10
-30
-40
-30
-50
-10
0
-20
-20
-50
即小明位于原来位置的西方50米
写成算式:(-20)+(-30)=-50
(3)若第一次向东走20米,第二次向西走了30米
10
30
-30
-20
-10
0
20
+20
-10
即小明位于原来位置的西方10米
写成算式:(+20)+(-30)=-10
(4)若第一次向西走20米,第二次向东走了30米
10
30
-20
+30
-10
0
20
-20
+10
即小明位于原来位置的东方10米
写成算式:(-20)+(+30)=+10
(1)若两次都是向东走,共向东走了50米
算式:(+20)+(+30)=+50
(2)若两次都是向西走,则共向西走了50米
算式:(-20)+(-30)=-50
(3)若第一次向东走20米,第二次向西走了30米
算式:(+20)+(-30)=-10
(4)若第一次向西走20米,第二次向东走了30米
算式:(-20)+(+30)=+10
从以上几种情况你能发现什么?
请你再举出像这样有理数加法的事例,并列出算式。
1.同号两数相加,
取与加数相同的正负号,并把绝对值相加。
2.绝对值不等的异号两数相加,
取绝对值较大的加数的正负号,并用较大的绝对值减去较小的绝对值。
四、归纳法则
再看下面的特殊情况
(5)若第一次向西走30米,第二次向东走了30 米。
+30
-30
10
-30
-20
-10
0
20
写成算式:(-30)+(+30)=( )
0
(6)若第一次向西走30米,第二次没走。
即小明回到原来的位置
写成算式:(-30)+(0)=( )
-30
即小明位于原来位置的西方30米
有理数的加法法则:
(1)同号两数相加,取与加数相同的正负号,并把绝对值相加。
(2)绝对值不等的异号两数相加,取绝对值较大的加 数的正负号,并用较大的绝对值减去较小的绝对值。
(3)互为相反数的两数相加得零。
(4)一个数与零相加,仍得这个数。
通过以上探索,想一下,两个有理数相加 “和的正负号”怎样确定?“和的绝对值”怎样确定?一个有理数同0相加,和是多少?
赶快动脑筋,说说自己的想法
注意:一个有理数由正负号和绝对值两部分组成,进行加法运算时,应注意先确定和的正负号,再确定和绝对值.
计算 1、(+3)+(-5)
2 、(-2)+(-4)
1、解:(+3)+(-5)
五、示范运用
2、解:(-2) + (-4)
=-(5-3)
=-2
=-(2 + 4)
=-6
加数
加数 和的组成
和
符号 绝对值
-12 3 - 12-3 -9
18 8
-9 16
-9 -5
+
18+8
+26
+
16-9
+7
-
9+5
-14
例题:1计算:
(1) (+2)+(-11) (2)(+20)+(+12)
(3) ( )+( ) (4) ( -3.2 )+4.3
六、强化训练
1、(+4)+(+3)= 2、(+4)+(-3)=
3、(+3)+(-10)= 4、(-5)+(+7)=
5、(-6)+(+2) = 6、(-4)+(-11)=
7、(+30)+(-30)= 8、(-2)+(+2)=
9、 0+(-23)= 10、(+16)+0=
+7
+1
-7
+2
-4
-15
0
0
-23
+16
七、快速检测
计算
现在我们可以来回答课堂开始的气温问题了吧。
1、两个正数,和是否一定大于每个加数?
2、两个有理数,和是否一定大于每个加数?
3、若∣a+1∣ +∣b-2∣=0,则a+b的值是多少?若∣a+1∣ +∣b-2∣+ ∣c+3∣ =0,则a+b+c的值呢?
八、拓展提升
4.两数相加,如果和比每个加数都小,那么这两个数( )
A、 同为负数 B、异号 C、同为正数
D、零或负数
5、如果两数的和为正数,那么一定有( )
A、一个加数为正,另一个加数为0
B、这两个加数都是正数
C、一个为正数,另一个为负数,且正数的绝对值较大
D、至少有一个加数为正数
A
D
6、两数相加,如果和比其中一个加数大,而比另一个加数小,那么这两个数( )
A、同为负数 B、异号
C、同为正数 D、有一个是0
B
九、小结与回顾
这节课的收获是……
1.这节课我们从实例出发,经过比较、归纳,得出了有理数加法的法则.今后我们经常要用类似的思想方法研究其他问题。
2.我们知道了有理数法则并能用有理数法则进行有理数加法运算。
3.应用有理数加法法则进行计算时,要同时注意确定“和”的符号,计算“和”的绝对值两件事。?
1.课本P34页,习题2.6 1,2,
2.预习课本P32—P33
十、布置作业
同学们,今天我们在数学上学习了有理数的加法运算法则,其实我们的人生、学习等方面从某些意义上来讲也是在做加法运算,如果某一天我们不努力,我们加的收获加数就小,或者说是0,甚至可能是负数,我们的收获积累就会或是增长很小,或是停止不前,或是倒退。因此,为了我们有丰富的学识和辉煌的人生,我们每一天都应该积极努力,尽力增大我们的每一个成长加数。
结束语:
华东师范大学出版社
一、引入课题
同学们,现已金秋,秋高气爽,据网上气温资料显示,昨天早晨8点我们这里的气温是20℃,到了午后的13点气温上升了5℃,但是到了下午的17点气温又下降了4℃,你能知道13点和17点的气温各是多少吗?
二、学习目标
1.理解有理数加法法则的意义,掌握有理数的加法法则。
2. 能运用有理数的加法法则进行有理数的加法运算。??
重点、难点
1.重点:有理数加法法则。
2.难点:异号两数相加的法则 。
三、新知探究
问题:
小明在一条东西方向的直道上,先走了20米,又走了30米,能否确定他现在位于原来位置的哪个方向,与原来位置相距多少米?
(1)若两次都是向东走
(2)若两次都是向西走
(3)若第一次向东走20米,第二次向西走了30米
(4)若第一次向西走20米,第二次向东走了30米
试验:
因为这个问题涉及到方向,不妨规定向东为正,向西为负。
(1)若两次都是向东走,
10
30
40
+30
50
-10
0
20
+20
+50
即小明位于原来位置的东方50米
写成算式:(+20)+(+30)=+50
(2)若两次都是向西走,
10
-30
-40
-30
-50
-10
0
-20
-20
-50
即小明位于原来位置的西方50米
写成算式:(-20)+(-30)=-50
(3)若第一次向东走20米,第二次向西走了30米
10
30
-30
-20
-10
0
20
+20
-10
即小明位于原来位置的西方10米
写成算式:(+20)+(-30)=-10
(4)若第一次向西走20米,第二次向东走了30米
10
30
-20
+30
-10
0
20
-20
+10
即小明位于原来位置的东方10米
写成算式:(-20)+(+30)=+10
(1)若两次都是向东走,共向东走了50米
算式:(+20)+(+30)=+50
(2)若两次都是向西走,则共向西走了50米
算式:(-20)+(-30)=-50
(3)若第一次向东走20米,第二次向西走了30米
算式:(+20)+(-30)=-10
(4)若第一次向西走20米,第二次向东走了30米
算式:(-20)+(+30)=+10
从以上几种情况你能发现什么?
请你再举出像这样有理数加法的事例,并列出算式。
1.同号两数相加,
取与加数相同的正负号,并把绝对值相加。
2.绝对值不等的异号两数相加,
取绝对值较大的加数的正负号,并用较大的绝对值减去较小的绝对值。
四、归纳法则
再看下面的特殊情况
(5)若第一次向西走30米,第二次向东走了30 米。
+30
-30
10
-30
-20
-10
0
20
写成算式:(-30)+(+30)=( )
0
(6)若第一次向西走30米,第二次没走。
即小明回到原来的位置
写成算式:(-30)+(0)=( )
-30
即小明位于原来位置的西方30米
有理数的加法法则:
(1)同号两数相加,取与加数相同的正负号,并把绝对值相加。
(2)绝对值不等的异号两数相加,取绝对值较大的加 数的正负号,并用较大的绝对值减去较小的绝对值。
(3)互为相反数的两数相加得零。
(4)一个数与零相加,仍得这个数。
通过以上探索,想一下,两个有理数相加 “和的正负号”怎样确定?“和的绝对值”怎样确定?一个有理数同0相加,和是多少?
赶快动脑筋,说说自己的想法
注意:一个有理数由正负号和绝对值两部分组成,进行加法运算时,应注意先确定和的正负号,再确定和绝对值.
计算 1、(+3)+(-5)
2 、(-2)+(-4)
1、解:(+3)+(-5)
五、示范运用
2、解:(-2) + (-4)
=-(5-3)
=-2
=-(2 + 4)
=-6
加数
加数 和的组成
和
符号 绝对值
-12 3 - 12-3 -9
18 8
-9 16
-9 -5
+
18+8
+26
+
16-9
+7
-
9+5
-14
例题:1计算:
(1) (+2)+(-11) (2)(+20)+(+12)
(3) ( )+( ) (4) ( -3.2 )+4.3
六、强化训练
1、(+4)+(+3)= 2、(+4)+(-3)=
3、(+3)+(-10)= 4、(-5)+(+7)=
5、(-6)+(+2) = 6、(-4)+(-11)=
7、(+30)+(-30)= 8、(-2)+(+2)=
9、 0+(-23)= 10、(+16)+0=
+7
+1
-7
+2
-4
-15
0
0
-23
+16
七、快速检测
计算
现在我们可以来回答课堂开始的气温问题了吧。
1、两个正数,和是否一定大于每个加数?
2、两个有理数,和是否一定大于每个加数?
3、若∣a+1∣ +∣b-2∣=0,则a+b的值是多少?若∣a+1∣ +∣b-2∣+ ∣c+3∣ =0,则a+b+c的值呢?
八、拓展提升
4.两数相加,如果和比每个加数都小,那么这两个数( )
A、 同为负数 B、异号 C、同为正数
D、零或负数
5、如果两数的和为正数,那么一定有( )
A、一个加数为正,另一个加数为0
B、这两个加数都是正数
C、一个为正数,另一个为负数,且正数的绝对值较大
D、至少有一个加数为正数
A
D
6、两数相加,如果和比其中一个加数大,而比另一个加数小,那么这两个数( )
A、同为负数 B、异号
C、同为正数 D、有一个是0
B
九、小结与回顾
这节课的收获是……
1.这节课我们从实例出发,经过比较、归纳,得出了有理数加法的法则.今后我们经常要用类似的思想方法研究其他问题。
2.我们知道了有理数法则并能用有理数法则进行有理数加法运算。
3.应用有理数加法法则进行计算时,要同时注意确定“和”的符号,计算“和”的绝对值两件事。?
1.课本P34页,习题2.6 1,2,
2.预习课本P32—P33
十、布置作业
同学们,今天我们在数学上学习了有理数的加法运算法则,其实我们的人生、学习等方面从某些意义上来讲也是在做加法运算,如果某一天我们不努力,我们加的收获加数就小,或者说是0,甚至可能是负数,我们的收获积累就会或是增长很小,或是停止不前,或是倒退。因此,为了我们有丰富的学识和辉煌的人生,我们每一天都应该积极努力,尽力增大我们的每一个成长加数。
结束语:
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
