华师大版七年级数学上册3.4.2合并同类项课件(共15张PPT)
文档属性
| 名称 | 华师大版七年级数学上册3.4.2合并同类项课件(共15张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 332.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-05 15:38:09 | ||
图片预览






文档简介
(共15张PPT)
3.4.2 合并同类项
5
n
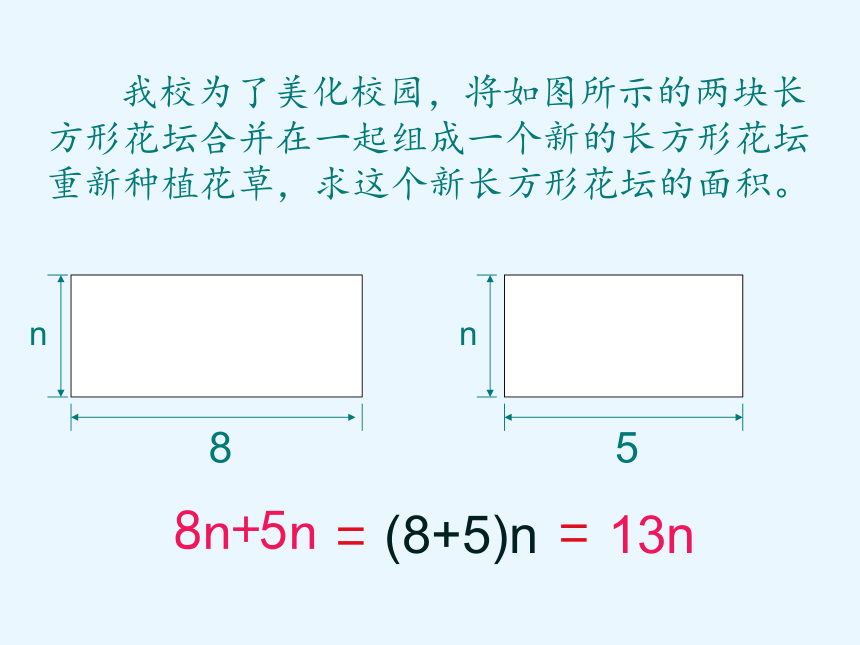
我校为了美化校园,将如图所示的两块长方形花坛合并在一起组成一个新的长方形花坛重新种植花草,求这个新长方形花坛的面积。
8
n
8n+5n
(8+5)n
13n
=
=
思考:(1)观察上面的式子,你发现了什么?
(2)你能归纳出合并同类项的法则吗?
定义:把同类项合成一项,叫做合并同类项。
8n+5n
(8+5)n
13n
=
=
合并同类
项的法则
把同类项的系数相加,所得的结果作为系数,字母和字母的指数保持不变。
系数来相加,其它不变样。
我来帮你
记一记
如:
×
×
×
√
辨一辨:下列各题合并同类项的结果对不对?对的打 ,错的打 请指出错在哪里?
√
×
一、找出
二、交换
三、合并
解:原式=
例:合并下列多项式中的同类项
结合
合并下列多项式中的同类项。
(1)
(2)
解:(1)原式=
(2)
找出
交换结合
合并
注意:
(1)用画线的方法标出各多项式中的同类
项,以减少运算的错误。
(2)移项时要带着原来的符号一起移动。
(3)把同类项用括号放在一起时用加号连接。
(4 )两个同类项的系数互为相反数时,合并同类项,结果为零。
先标出下列各多项式中的同类项,
再合并同类项。
解:原式=
(1)
解:原式=
(2)
求多项式3x +4x-2x -x+x -3x-1的值,
其中x=-3.
2
2
2
解:
3x +4x-2x -x+x -3x-1
2
2
2
=(3-2+1)x +(4-1-3)x-1
2
=2x -1
2
当x=-3时,原式=2x(-3) -1=17
2
想一想:如果x=0如何求值比较简便?
先合并同类项,再求值比较简便
1:当k= 时,多项式2x2+7kxy+3y2+x-7xy+5y
中不含xy项
解:原式=2x2+(7kxy-7xy)+3y2+x+5y
=2x2+(7k-7)xy+3y2+x+5y
∵多项式中不含xy项,
∴其系数为0,即(7k-7)=0
∴k=1
1
2 :
若 ,则( )
A.a=1,b=3 B.a=3,b=2
C.a=2,b=2 D.以上答案都不对。
B
解此类题关键在于,能识别出题中的同类项,这是一个隐含条件,需要深入分析才能找出。
合并同类项法则:
把同类项的系数相加,所得的结果作
为系数,字母和字母的指数保持不变.
注意:
(1)合并的前提是有同类项,不是同类项不能合并。
(2)移项时要带着原来的符号一起移动。
(3)把同类项用括号放在一起时用加号连接。
(4)只是系数相加,其它不变样。
说一说本节课的收获:
作业布置:
课本P112,第5、6题
谢谢!
3.4.2 合并同类项
5
n
我校为了美化校园,将如图所示的两块长方形花坛合并在一起组成一个新的长方形花坛重新种植花草,求这个新长方形花坛的面积。
8
n
8n+5n
(8+5)n
13n
=
=
思考:(1)观察上面的式子,你发现了什么?
(2)你能归纳出合并同类项的法则吗?
定义:把同类项合成一项,叫做合并同类项。
8n+5n
(8+5)n
13n
=
=
合并同类
项的法则
把同类项的系数相加,所得的结果作为系数,字母和字母的指数保持不变。
系数来相加,其它不变样。
我来帮你
记一记
如:
×
×
×
√
辨一辨:下列各题合并同类项的结果对不对?对的打 ,错的打 请指出错在哪里?
√
×
一、找出
二、交换
三、合并
解:原式=
例:合并下列多项式中的同类项
结合
合并下列多项式中的同类项。
(1)
(2)
解:(1)原式=
(2)
找出
交换结合
合并
注意:
(1)用画线的方法标出各多项式中的同类
项,以减少运算的错误。
(2)移项时要带着原来的符号一起移动。
(3)把同类项用括号放在一起时用加号连接。
(4 )两个同类项的系数互为相反数时,合并同类项,结果为零。
先标出下列各多项式中的同类项,
再合并同类项。
解:原式=
(1)
解:原式=
(2)
求多项式3x +4x-2x -x+x -3x-1的值,
其中x=-3.
2
2
2
解:
3x +4x-2x -x+x -3x-1
2
2
2
=(3-2+1)x +(4-1-3)x-1
2
=2x -1
2
当x=-3时,原式=2x(-3) -1=17
2
想一想:如果x=0如何求值比较简便?
先合并同类项,再求值比较简便
1:当k= 时,多项式2x2+7kxy+3y2+x-7xy+5y
中不含xy项
解:原式=2x2+(7kxy-7xy)+3y2+x+5y
=2x2+(7k-7)xy+3y2+x+5y
∵多项式中不含xy项,
∴其系数为0,即(7k-7)=0
∴k=1
1
2 :
若 ,则( )
A.a=1,b=3 B.a=3,b=2
C.a=2,b=2 D.以上答案都不对。
B
解此类题关键在于,能识别出题中的同类项,这是一个隐含条件,需要深入分析才能找出。
合并同类项法则:
把同类项的系数相加,所得的结果作
为系数,字母和字母的指数保持不变.
注意:
(1)合并的前提是有同类项,不是同类项不能合并。
(2)移项时要带着原来的符号一起移动。
(3)把同类项用括号放在一起时用加号连接。
(4)只是系数相加,其它不变样。
说一说本节课的收获:
作业布置:
课本P112,第5、6题
谢谢!
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
