2021华师大版七年级数学上册4.5.2线段的长短比较课件(16张)
文档属性
| 名称 | 2021华师大版七年级数学上册4.5.2线段的长短比较课件(16张) |  | |
| 格式 | ppt | ||
| 文件大小 | 383.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-06 08:27:37 | ||
图片预览

文档简介
(共16张PPT)
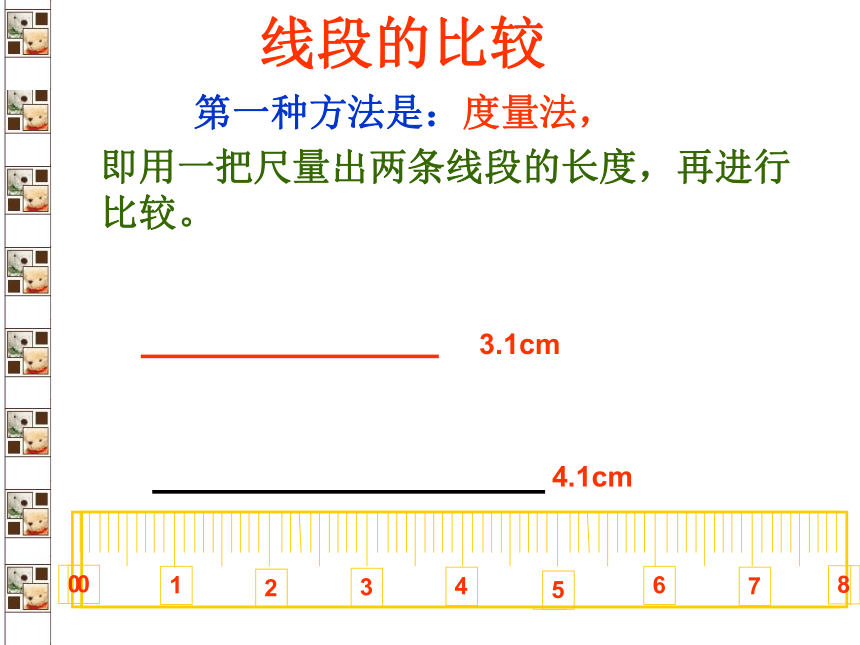
第一种方法是:度量法,
1
2
3
5
4
6
7
8
0
3.1cm
4.1cm
1
2
3
5
4
6
7
8
0
线段的比较
即用一把尺量出两条线段的长度,再进行比较。
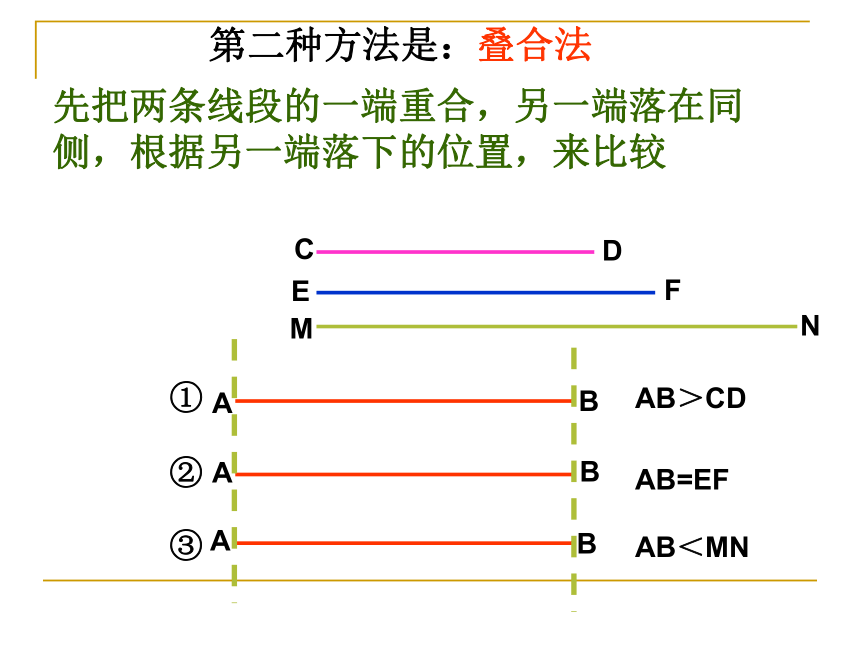
第二种方法是:叠合法
①
②
③
A
B
B
A
A
B
C
D
E
F
M
N
AB>CD
AB=EF
AB<MN
先把两条线段的一端重合,另一端落在同侧,根据另一端落下的位置,来比较
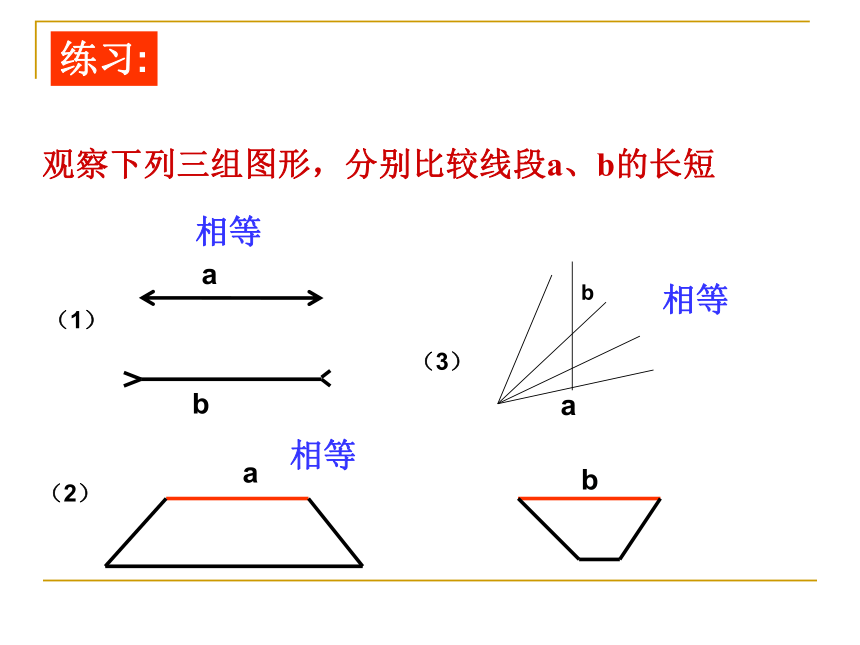
练习:
观察下列三组图形,分别比较线段a、b的长短
(1)
a
b
(3)
(2)
a
b
a
b
相等
相等
相等
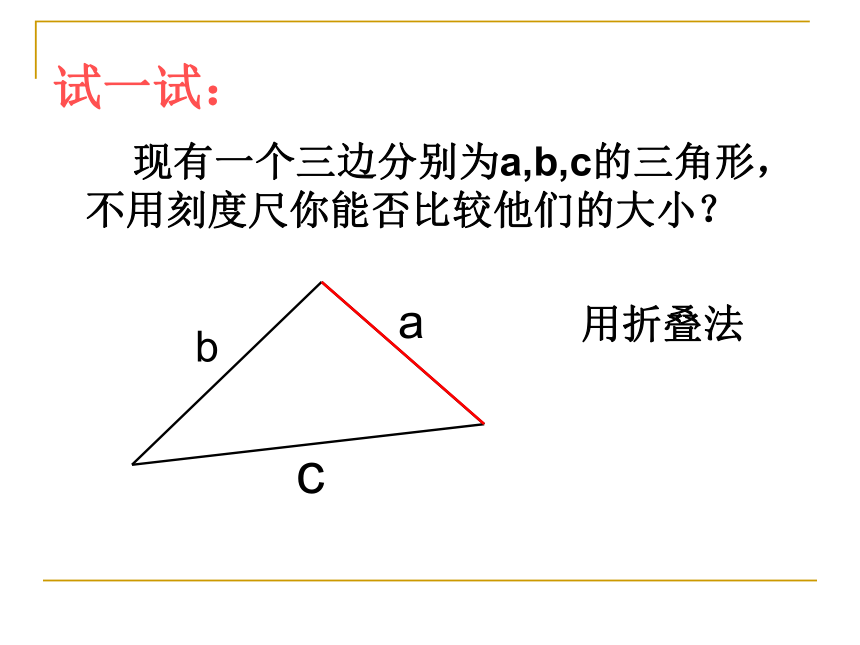
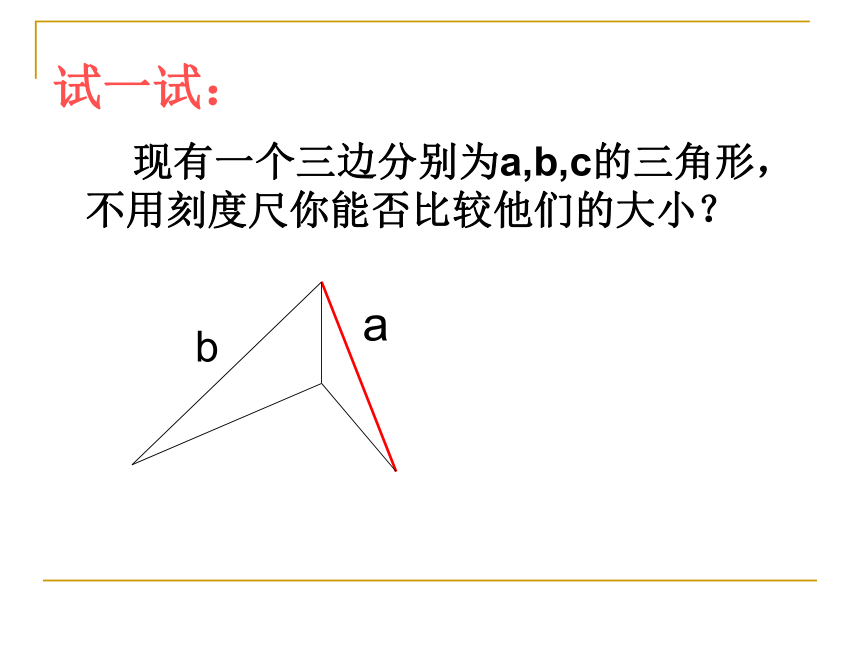
试一试:
现有一个三边分别为a,b,c的三角形,不用刻度尺你能否比较他们的大小?
a
b
c
用折叠法
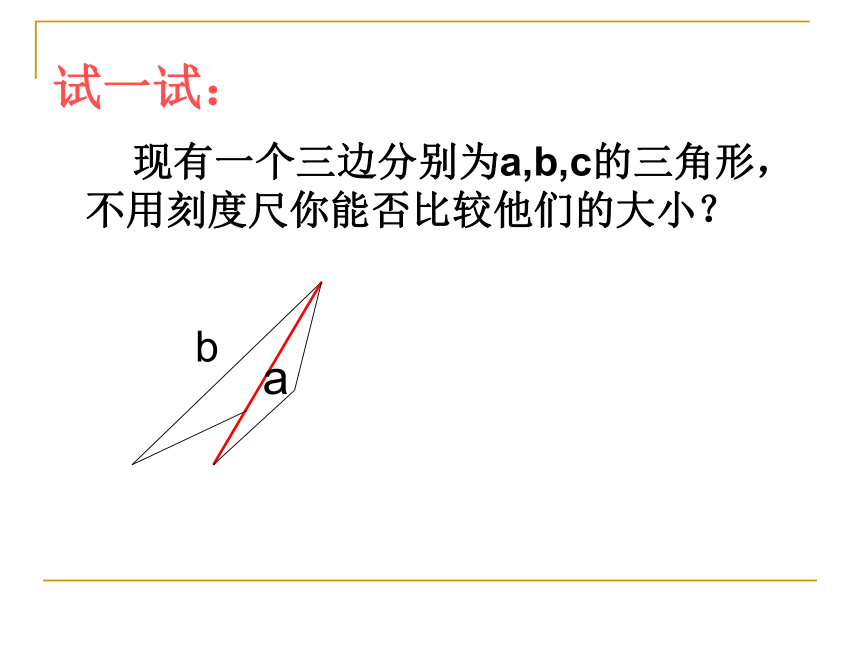
试一试:
现有一个三边分别为a,b,c的三角形,不用刻度尺你能否比较他们的大小?
a
b
试一试:
现有一个三边分别为a,b,c的三角形,不用刻度尺你能否比较他们的大小?
a
b
试一试:
现有一个三边分别为a,b,c的三角形,不用刻度尺你能否比较他们的大小?
a
b
试一试:
现有一个三边分别为a,b,c的三角形,不用刻度尺你能否比较他们的大小?
a
b
c
试一试:
现有一个三边分别为a,b,c的三角形,不用刻度尺你能否比较他们的大小?
b
c
试一试:
现有一个三边分别为a,b,c的三角形,不用刻度尺你能否比较他们的大小?
b
c
试一试:
现有一个三边分别为a,b,c的三角形,不用刻度尺你能否比较他们的大小?
b
c
把一条线段分成两条相等线段的点,叫做这条线段的中点。
线段的中点
A
B
C
如图,若C为线段AB的中点,则有如下等式成立:
(1)AC=CB
(2)AC=CB= AB
(3)AB=2AC=2CB
例3. 如图,AB=6cm,点C是线段AB的中点,点D是线段CB的中点,那么AD有多长呢?
∴AC=CB=
A
D
C
B
解:∵点C是线段AB的中点
中点应用
答:AD的长度为4.5cm
∵点D是线段CB的中点
还有其他的解法吗?
解法二:
∵点C是线段AB的中点
∴ AC=CB=
A
D
C
B
答:AD的长度为4.5cm
∵点D是线段CB的中点
如何比较两条线段的大小。
2. 了解两条线段的和与差仍是线段。
3. 学会线段的中点定义及相关计算。
第一种方法是:度量法,
1
2
3
5
4
6
7
8
0
3.1cm
4.1cm
1
2
3
5
4
6
7
8
0
线段的比较
即用一把尺量出两条线段的长度,再进行比较。
第二种方法是:叠合法
①
②
③
A
B
B
A
A
B
C
D
E
F
M
N
AB>CD
AB=EF
AB<MN
先把两条线段的一端重合,另一端落在同侧,根据另一端落下的位置,来比较
练习:
观察下列三组图形,分别比较线段a、b的长短
(1)
a
b
(3)
(2)
a
b
a
b
相等
相等
相等
试一试:
现有一个三边分别为a,b,c的三角形,不用刻度尺你能否比较他们的大小?
a
b
c
用折叠法
试一试:
现有一个三边分别为a,b,c的三角形,不用刻度尺你能否比较他们的大小?
a
b
试一试:
现有一个三边分别为a,b,c的三角形,不用刻度尺你能否比较他们的大小?
a
b
试一试:
现有一个三边分别为a,b,c的三角形,不用刻度尺你能否比较他们的大小?
a
b
试一试:
现有一个三边分别为a,b,c的三角形,不用刻度尺你能否比较他们的大小?
a
b
c
试一试:
现有一个三边分别为a,b,c的三角形,不用刻度尺你能否比较他们的大小?
b
c
试一试:
现有一个三边分别为a,b,c的三角形,不用刻度尺你能否比较他们的大小?
b
c
试一试:
现有一个三边分别为a,b,c的三角形,不用刻度尺你能否比较他们的大小?
b
c
把一条线段分成两条相等线段的点,叫做这条线段的中点。
线段的中点
A
B
C
如图,若C为线段AB的中点,则有如下等式成立:
(1)AC=CB
(2)AC=CB= AB
(3)AB=2AC=2CB
例3. 如图,AB=6cm,点C是线段AB的中点,点D是线段CB的中点,那么AD有多长呢?
∴AC=CB=
A
D
C
B
解:∵点C是线段AB的中点
中点应用
答:AD的长度为4.5cm
∵点D是线段CB的中点
还有其他的解法吗?
解法二:
∵点C是线段AB的中点
∴ AC=CB=
A
D
C
B
答:AD的长度为4.5cm
∵点D是线段CB的中点
如何比较两条线段的大小。
2. 了解两条线段的和与差仍是线段。
3. 学会线段的中点定义及相关计算。
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
