陕西省咸阳市三原县城关北城高级中学2021-2022学年高二上学期11月月考数学试卷(Word版,含答案)
文档属性
| 名称 | 陕西省咸阳市三原县城关北城高级中学2021-2022学年高二上学期11月月考数学试卷(Word版,含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 557.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-06 16:01:58 | ||
图片预览




文档简介
北城高级中学2021-2022学年高二上学期11月月考
数学试卷
一、单选题
1.已知命题 , ;命题 , ,则命题 是命题 的( )
A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件
2.已知等差数列 的前n项和 有最大值,且 ,则满足 的最大正整数 的值为( )
A. 6 B. 7 C. 11 D. 12
3.设 ,若 ,则展开式中二项式系数最大的项为( )
A. 第4项 B. 第5项 C. 第4项和第5项 D. 第7项
4.直线 恒过定点A,若点A是双曲线 的一条弦的中点,则此弦所在的直线方程为( )
A. B.
C. D.
5.椭圆 : 的左右焦点分别为 , ,抛物线 以 为焦点,且椭圆与抛物线在第一象限交于点 ,若 ,则椭圆C的离心率为( )
A. B. C. D.
6.已知点P(1,0)及圆C: ,点M,N在圆C上,若PM⊥PN,则 的取值范围为( )
A. B.
C. D.
7.设 ,那么“ ”是“ ”的( )
A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分又不必要条件
8.已知直线 ,圆 ,圆心为点C. 点 为直线l上的动点,过点 作圆 的切线 , ,切点分别为 , ,则四边形 面积的最小值为( )
A. B. C. D.
9.《莱因德纸草书》是世界上最古老的数学著作之一,书中有一道这样的题目:把100个面包分给五个人,使每个人所得成等差数列,最大的三份之和的 是最小的两份之和,则最小的一份的量是( )
A. B. C. D.
10.已知 为两条不同的直线, 为两个不同的平面,下列四个命题中正确的是( )
A. 若 且 则 B. 若 在 上,且 则
C. 若 且 在 上,则 D. 若 且 在 外,则
11.若某公司从五位大学毕业生甲、乙、丙、丁、戌中录用三人,这五人被录用的机会均等,则甲或乙被 录用的概率为( )
A. B. C. D.
12.在空间直角坐标系 中, , , , ,则 与平面 所成角的正弦值为( )
A. B. C. D.
13.三棱锥 的各棱长都相等, 分别是 的中点,下列四个结论中不成立的是( )
A. 平面 B. 平面
C. 平面 平面 D. 平面 平面
14.若方程 表示焦点在 轴上的椭圆,则实数 的取值范围是( ).
A. B.
C. D.
15.已知等腰梯形的上底长为7,腰长为2,那么该等腰梯形面积最大时的下底长为( )
A. 7.5 B. 8 C. 8.5 D. 9
16.已知椭圆 的左焦点为 ,点 是椭圆 的上顶点,直线 与椭圆 交于 、 两点.若点 到直线 的距离是1,且 ,则椭圆 的离心率是( )
A. B. C. D.
17.不等式 的解集是( )
A. , B. ,
C. D.
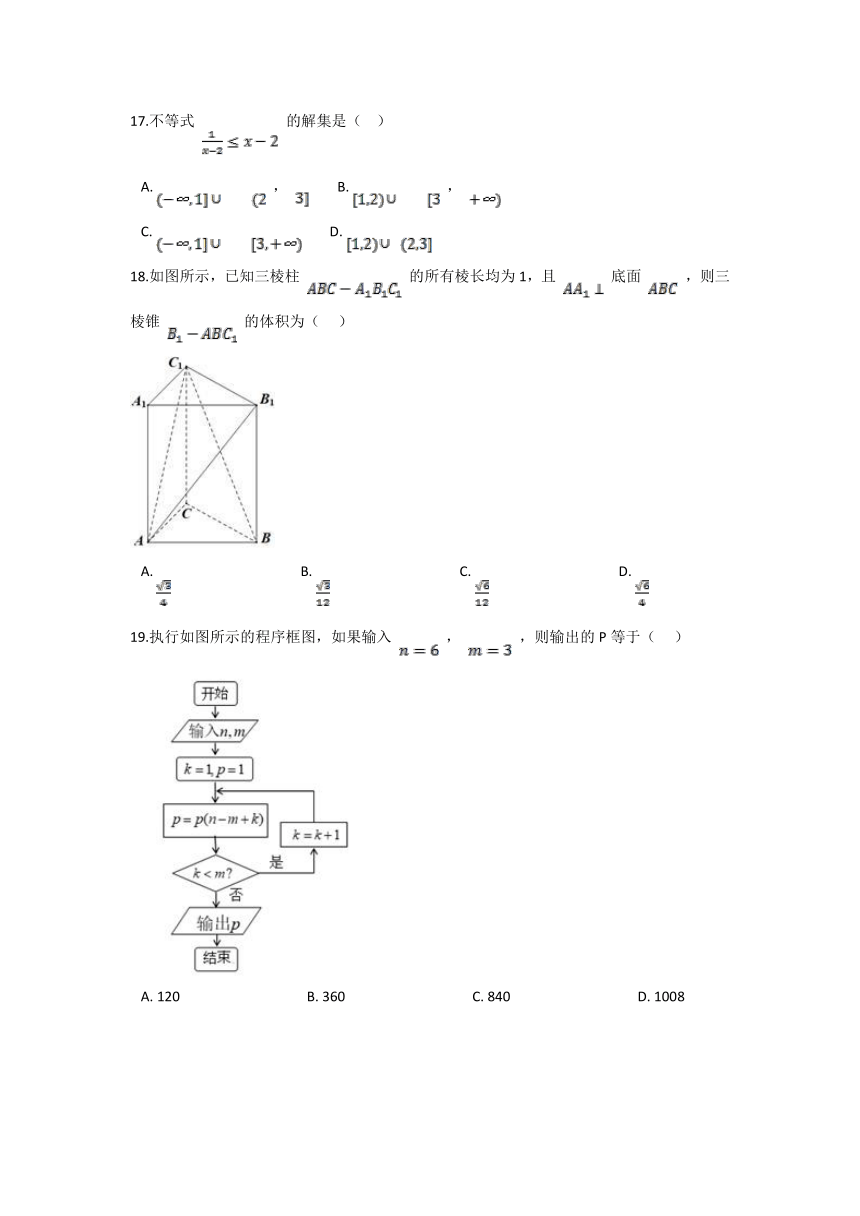
18.如图所示,已知三棱柱 的所有棱长均为1,且 底面 ,则三棱锥 的体积为( )
A. B. C. D.
19.执行如图所示的程序框图,如果输入 , ,则输出的P等于( )
A. 120 B. 360 C. 840 D. 1008
20.在四棱锥 中,底面ABCD是正方形,E为PD中点,若 , , ,则
A. ; B. C. D.
二、多选题
21.下列说法正确的是( )
A. 过 , 两点的直线方程为
B. 点 关于直线 的对称点为
C. 直线 与两坐标轴围成的三角形的面积是4
D. 经过点 且在 轴和 轴上截距都相等的直线方程为
22.下列命题中,正确的是( )
A.已知随机变量 服从正态分布 ,若 ,则
B.已知随机变量 的分布列为 ,则
C.用 表示 次独立重复试验中事件 发生的次数, 为每次试验中事件 发生的概率,若 ,则
D.已知某家系有甲和乙两种遗传病,该家系成员 患甲病的概率为 ,患乙病的概率为 ,甲乙两种病都不患的概率为 .则家系成员 在患甲病的条件下,患乙病的概率为
23.在2020年3月15日,某市物价部门对本市的5家商场的某商品的一天销售量及其价格进行调查,5家商场的售价 元和销售量 件之间的一组数据如表所示:
价格 9 9.5 10 10.5 11
销售量 11 10 8 6 5
根据公式计算得相关系数 ,其线性回归直线方程是: ,则下列说法正确的有( )
参考:
A. 有 的把握认为变量 具有线性相关关系 B. 回归直线恒过定点
C. D. 当 时, 的估计值为12.8
24.已知某三棱锥的三视图如图所示,则下列结论正确的是( )
A. 该三棱锥的所有棱长都相等 B. 该三棱锥的体积为
C. 该三棱锥的外接球表面积为 D. 该三棱锥内任意一点到各个面的距离之和等于它的高
25.已知双曲线 的离心率为2,点 , 是 上关于原点对称的两点,点 是 的右支上位于第一象限的动点(不与点 、 重合),记直线 , 的斜率分别为 , ,则下列结论正确的是( )
A. 以线段 为直径的圆与 可能有两条公切线
B.
C. 存在点 ,使得
D. 当 时,点 到 的两条渐近线的距离之积为3
三、填空题
26.焦点坐标为 和 ,且点 在椭圆上,那么这个椭圆的标准方程 .
27.在全运会期间,4名志愿者被安排参加三个不同比赛项目的接待服务工作,则每个项目至少有一人参加的安排方法有 .
28.在等比数列{an}中,若a4a6a8a10a12=243,则 的值为________.
29.我们知道:在长方形ABCD中,如果设AB=a,BC=b,那么长方形ABCD的外接圆的半径R满足:4R2=a2+b2 , 类比上述结论回答:在长方体ABCD﹣A1B1C1D1中,如果设AB=a,AD=b,AA1=c,那么长方体ABCD﹣A1B1C1D1的外接球的半径R满足的关系式是 .
30.已知向量 =3 ﹣4 , =(1﹣n) +3n ,若 ∥ ,则n的值为________.
四、解答题
31.设 ,g(x)=x3﹣x2﹣3.
(1)当a=2时,求曲线y=f(x)在x=1处的切线方程;
(2)如果存在x1 , x2∈[0,2],使得g(x1)﹣g(x2)≥M成立,求满足上述条件的最大整数M;
(3)如果对任意的 ,都有f(s)≥g(t)成立,求实数a的取值范围.
32.如图,在四面体ABCD中,CB=CD,AD⊥BD,点E,F分别是AB,BD的中点.
求证:
(Ⅰ)直线EF∥平面ACD;
(Ⅱ)平面EFC⊥平面BCD.
33.已知在 的展开式中,第5项的系数与第3项的系数之比是14∶1.
(1)求展开式中 的系数;
(2)求展开式中系数绝对值最大的项;
(3)求 的值.
34.等差数列 的前 项和为 ,且 , .
(1)求数列 的通项公式;
(2)若数列 满足 且 ,求数列 的前 项和 .
答案解析部分
一、单选题
1.【答案】 A
2.【答案】 C
3.【答案】 C
4.【答案】 D
5.【答案】 B
6.【答案】 A
7.【答案】 A
8.【答案】 B
9.【答案】 D
10.【答案】 D
11.【答案】 D
12.【答案】 A
13.【答案】 C
14.【答案】 B
15.【答案】 B
16.【答案】 D
17.【答案】 B
18.【答案】 B
19.【答案】 A
20.【答案】 C
二、多选题
21.【答案】 B,C
22.【答案】 A,C,D
23.【答案】 A,B,C,D
24.【答案】 A,B,D
25.【答案】 A,B,D
三、填空题
26.【答案】
27.【答案】 36
28.【答案】3
29.【答案】 4R2=a2+b2+c2
30.【答案】 或n∈R
四、解答题
31.【答案】 (1)解:当a=2时, , ,f(1)=2,f'(1)=﹣1,所以曲线y=f(x)在x=1处的切线方程为y=﹣x+3
(2)解:存在x1 , x2∈[0,2],使得g(x1)﹣g(x2)≥M成立
等价于:[g(x1)﹣g(x2)]max≥M,
考察g(x)=x3﹣x2﹣3, ,
由上表可知: ,
,
所以满足条件的最大整数M=4
(3)解:当 时, 恒成立
等价于a≥x﹣x2lnx恒成立,
记h(x)=x﹣x2lnx,h'(x)=1﹣2xlnx﹣x,h'(1)=0.
记m(x)=1﹣2xlnx﹣x,m'(x)=﹣3﹣2lnx,
由于 ,m'(x)=﹣3﹣2lnx<0,
所以m(x)=h'(x)=1﹣2xlnx﹣x在 上递减,
当 时,h'(x)>0,x∈(1,2]时,h'(x)<0,
即函数h(x)=x﹣x2lnx在区间 上递增,在区间(1,2]上递减,
所以h(x)max=h(1)=1,所以a≥1
32.【答案】 证明:(1)∵点E,F分别是AB,BD的中点.
∴EF∥AD,
又EF 面ACD,AD 面ACD,
∴EF∥面ACD;
(2)∵CB=CD,点F是BD的中点.
∴BD⊥CF,
又AD⊥BD,EF∥AD,
∴EF⊥BD,
CF∩EF=F,
∴BD⊥面CEF,
BD 面BCD,
∴平面EFC⊥平面BCD.
33.【答案】 (1)解:由题意得 ,解得 .
通项为 ,令 ,得 ,
于是系数为
(2)解:设第 项系数的绝对值最大,则 解得 ,于是 只能为6,所以系数绝对值最大的项为
(3)解:原式
34.【答案】 (1)解:设等差数列 的公差为 ,
∵ ∴ ,
解得 .∴
(2)解:∵ , ,
当 时,
当 时, 适合上式,所以
.
.
数学试卷
一、单选题
1.已知命题 , ;命题 , ,则命题 是命题 的( )
A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件
2.已知等差数列 的前n项和 有最大值,且 ,则满足 的最大正整数 的值为( )
A. 6 B. 7 C. 11 D. 12
3.设 ,若 ,则展开式中二项式系数最大的项为( )
A. 第4项 B. 第5项 C. 第4项和第5项 D. 第7项
4.直线 恒过定点A,若点A是双曲线 的一条弦的中点,则此弦所在的直线方程为( )
A. B.
C. D.
5.椭圆 : 的左右焦点分别为 , ,抛物线 以 为焦点,且椭圆与抛物线在第一象限交于点 ,若 ,则椭圆C的离心率为( )
A. B. C. D.
6.已知点P(1,0)及圆C: ,点M,N在圆C上,若PM⊥PN,则 的取值范围为( )
A. B.
C. D.
7.设 ,那么“ ”是“ ”的( )
A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分又不必要条件
8.已知直线 ,圆 ,圆心为点C. 点 为直线l上的动点,过点 作圆 的切线 , ,切点分别为 , ,则四边形 面积的最小值为( )
A. B. C. D.
9.《莱因德纸草书》是世界上最古老的数学著作之一,书中有一道这样的题目:把100个面包分给五个人,使每个人所得成等差数列,最大的三份之和的 是最小的两份之和,则最小的一份的量是( )
A. B. C. D.
10.已知 为两条不同的直线, 为两个不同的平面,下列四个命题中正确的是( )
A. 若 且 则 B. 若 在 上,且 则
C. 若 且 在 上,则 D. 若 且 在 外,则
11.若某公司从五位大学毕业生甲、乙、丙、丁、戌中录用三人,这五人被录用的机会均等,则甲或乙被 录用的概率为( )
A. B. C. D.
12.在空间直角坐标系 中, , , , ,则 与平面 所成角的正弦值为( )
A. B. C. D.
13.三棱锥 的各棱长都相等, 分别是 的中点,下列四个结论中不成立的是( )
A. 平面 B. 平面
C. 平面 平面 D. 平面 平面
14.若方程 表示焦点在 轴上的椭圆,则实数 的取值范围是( ).
A. B.
C. D.
15.已知等腰梯形的上底长为7,腰长为2,那么该等腰梯形面积最大时的下底长为( )
A. 7.5 B. 8 C. 8.5 D. 9
16.已知椭圆 的左焦点为 ,点 是椭圆 的上顶点,直线 与椭圆 交于 、 两点.若点 到直线 的距离是1,且 ,则椭圆 的离心率是( )
A. B. C. D.
17.不等式 的解集是( )
A. , B. ,
C. D.
18.如图所示,已知三棱柱 的所有棱长均为1,且 底面 ,则三棱锥 的体积为( )
A. B. C. D.
19.执行如图所示的程序框图,如果输入 , ,则输出的P等于( )
A. 120 B. 360 C. 840 D. 1008
20.在四棱锥 中,底面ABCD是正方形,E为PD中点,若 , , ,则
A. ; B. C. D.
二、多选题
21.下列说法正确的是( )
A. 过 , 两点的直线方程为
B. 点 关于直线 的对称点为
C. 直线 与两坐标轴围成的三角形的面积是4
D. 经过点 且在 轴和 轴上截距都相等的直线方程为
22.下列命题中,正确的是( )
A.已知随机变量 服从正态分布 ,若 ,则
B.已知随机变量 的分布列为 ,则
C.用 表示 次独立重复试验中事件 发生的次数, 为每次试验中事件 发生的概率,若 ,则
D.已知某家系有甲和乙两种遗传病,该家系成员 患甲病的概率为 ,患乙病的概率为 ,甲乙两种病都不患的概率为 .则家系成员 在患甲病的条件下,患乙病的概率为
23.在2020年3月15日,某市物价部门对本市的5家商场的某商品的一天销售量及其价格进行调查,5家商场的售价 元和销售量 件之间的一组数据如表所示:
价格 9 9.5 10 10.5 11
销售量 11 10 8 6 5
根据公式计算得相关系数 ,其线性回归直线方程是: ,则下列说法正确的有( )
参考:
A. 有 的把握认为变量 具有线性相关关系 B. 回归直线恒过定点
C. D. 当 时, 的估计值为12.8
24.已知某三棱锥的三视图如图所示,则下列结论正确的是( )
A. 该三棱锥的所有棱长都相等 B. 该三棱锥的体积为
C. 该三棱锥的外接球表面积为 D. 该三棱锥内任意一点到各个面的距离之和等于它的高
25.已知双曲线 的离心率为2,点 , 是 上关于原点对称的两点,点 是 的右支上位于第一象限的动点(不与点 、 重合),记直线 , 的斜率分别为 , ,则下列结论正确的是( )
A. 以线段 为直径的圆与 可能有两条公切线
B.
C. 存在点 ,使得
D. 当 时,点 到 的两条渐近线的距离之积为3
三、填空题
26.焦点坐标为 和 ,且点 在椭圆上,那么这个椭圆的标准方程 .
27.在全运会期间,4名志愿者被安排参加三个不同比赛项目的接待服务工作,则每个项目至少有一人参加的安排方法有 .
28.在等比数列{an}中,若a4a6a8a10a12=243,则 的值为________.
29.我们知道:在长方形ABCD中,如果设AB=a,BC=b,那么长方形ABCD的外接圆的半径R满足:4R2=a2+b2 , 类比上述结论回答:在长方体ABCD﹣A1B1C1D1中,如果设AB=a,AD=b,AA1=c,那么长方体ABCD﹣A1B1C1D1的外接球的半径R满足的关系式是 .
30.已知向量 =3 ﹣4 , =(1﹣n) +3n ,若 ∥ ,则n的值为________.
四、解答题
31.设 ,g(x)=x3﹣x2﹣3.
(1)当a=2时,求曲线y=f(x)在x=1处的切线方程;
(2)如果存在x1 , x2∈[0,2],使得g(x1)﹣g(x2)≥M成立,求满足上述条件的最大整数M;
(3)如果对任意的 ,都有f(s)≥g(t)成立,求实数a的取值范围.
32.如图,在四面体ABCD中,CB=CD,AD⊥BD,点E,F分别是AB,BD的中点.
求证:
(Ⅰ)直线EF∥平面ACD;
(Ⅱ)平面EFC⊥平面BCD.
33.已知在 的展开式中,第5项的系数与第3项的系数之比是14∶1.
(1)求展开式中 的系数;
(2)求展开式中系数绝对值最大的项;
(3)求 的值.
34.等差数列 的前 项和为 ,且 , .
(1)求数列 的通项公式;
(2)若数列 满足 且 ,求数列 的前 项和 .
答案解析部分
一、单选题
1.【答案】 A
2.【答案】 C
3.【答案】 C
4.【答案】 D
5.【答案】 B
6.【答案】 A
7.【答案】 A
8.【答案】 B
9.【答案】 D
10.【答案】 D
11.【答案】 D
12.【答案】 A
13.【答案】 C
14.【答案】 B
15.【答案】 B
16.【答案】 D
17.【答案】 B
18.【答案】 B
19.【答案】 A
20.【答案】 C
二、多选题
21.【答案】 B,C
22.【答案】 A,C,D
23.【答案】 A,B,C,D
24.【答案】 A,B,D
25.【答案】 A,B,D
三、填空题
26.【答案】
27.【答案】 36
28.【答案】3
29.【答案】 4R2=a2+b2+c2
30.【答案】 或n∈R
四、解答题
31.【答案】 (1)解:当a=2时, , ,f(1)=2,f'(1)=﹣1,所以曲线y=f(x)在x=1处的切线方程为y=﹣x+3
(2)解:存在x1 , x2∈[0,2],使得g(x1)﹣g(x2)≥M成立
等价于:[g(x1)﹣g(x2)]max≥M,
考察g(x)=x3﹣x2﹣3, ,
由上表可知: ,
,
所以满足条件的最大整数M=4
(3)解:当 时, 恒成立
等价于a≥x﹣x2lnx恒成立,
记h(x)=x﹣x2lnx,h'(x)=1﹣2xlnx﹣x,h'(1)=0.
记m(x)=1﹣2xlnx﹣x,m'(x)=﹣3﹣2lnx,
由于 ,m'(x)=﹣3﹣2lnx<0,
所以m(x)=h'(x)=1﹣2xlnx﹣x在 上递减,
当 时,h'(x)>0,x∈(1,2]时,h'(x)<0,
即函数h(x)=x﹣x2lnx在区间 上递增,在区间(1,2]上递减,
所以h(x)max=h(1)=1,所以a≥1
32.【答案】 证明:(1)∵点E,F分别是AB,BD的中点.
∴EF∥AD,
又EF 面ACD,AD 面ACD,
∴EF∥面ACD;
(2)∵CB=CD,点F是BD的中点.
∴BD⊥CF,
又AD⊥BD,EF∥AD,
∴EF⊥BD,
CF∩EF=F,
∴BD⊥面CEF,
BD 面BCD,
∴平面EFC⊥平面BCD.
33.【答案】 (1)解:由题意得 ,解得 .
通项为 ,令 ,得 ,
于是系数为
(2)解:设第 项系数的绝对值最大,则 解得 ,于是 只能为6,所以系数绝对值最大的项为
(3)解:原式
34.【答案】 (1)解:设等差数列 的公差为 ,
∵ ∴ ,
解得 .∴
(2)解:∵ , ,
当 时,
当 时, 适合上式,所以
.
.
同课章节目录
