2.4 线段 角的轴对称性(3)课件(共15张PPT)
文档属性
| 名称 | 2.4 线段 角的轴对称性(3)课件(共15张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-05 00:00:00 | ||
图片预览




文档简介
(共15张PPT)
苏科版 八年级上
苏科版八年级上册
2.4线段角的轴对称性(3)
1、使学生掌握角是轴对称图形,角平分线的性质.
2、使学生通过类比的思想和方法掌握本节课的内容,培养学生主动探索学习的能力
3、通过类比方法,掌握了新的知识,提高学生自学的兴趣和信心.
学习目标
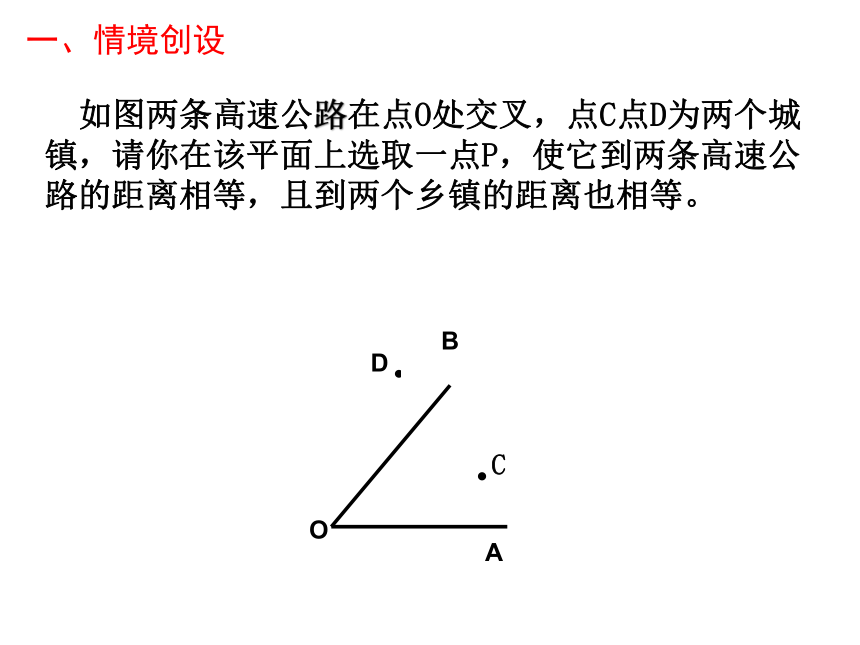
如图两条高速公路在点O处交叉,点C点D为两个城镇,请你在该平面上选取一点P,使它到两条高速公路的距离相等,且到两个乡镇的距离也相等。
O
A
B
C
D
一、情境创设
1、请同学们将事先准备的薄纸拿出来,在上面任意画一个角
(∠AOB),折纸使两边OA、OB重合,你发现折痕与∠AOB
有什么关系?你有什么结论:
二. 自主探究
问题1 角是轴对称图形吗?对称轴是什么?
角是轴对称图形,角平分线所在的直线是它的对称轴.
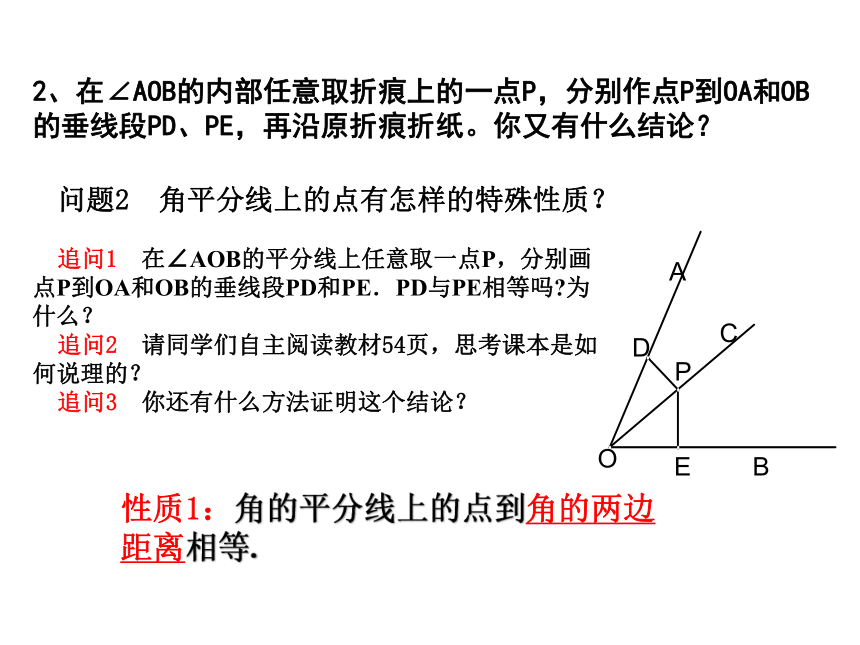
2、在∠AOB的内部任意取折痕上的一点P,分别作点P到OA和OB的垂线段PD、PE,再沿原折痕折纸。你又有什么结论?
问题2 角平分线上的点有怎样的特殊性质?
追问1 在∠AOB的平分线上任意取一点P,分别画点P到OA和OB的垂线段PD和PE.PD与PE相等吗 为什么?
追问2 请同学们自主阅读教材54页,思考课本是如何说理的?
追问3 你还有什么方法证明这个结论?
性质1:角的平分线上的点到角的两边距离相等.
O
D
E
A
B
P
C
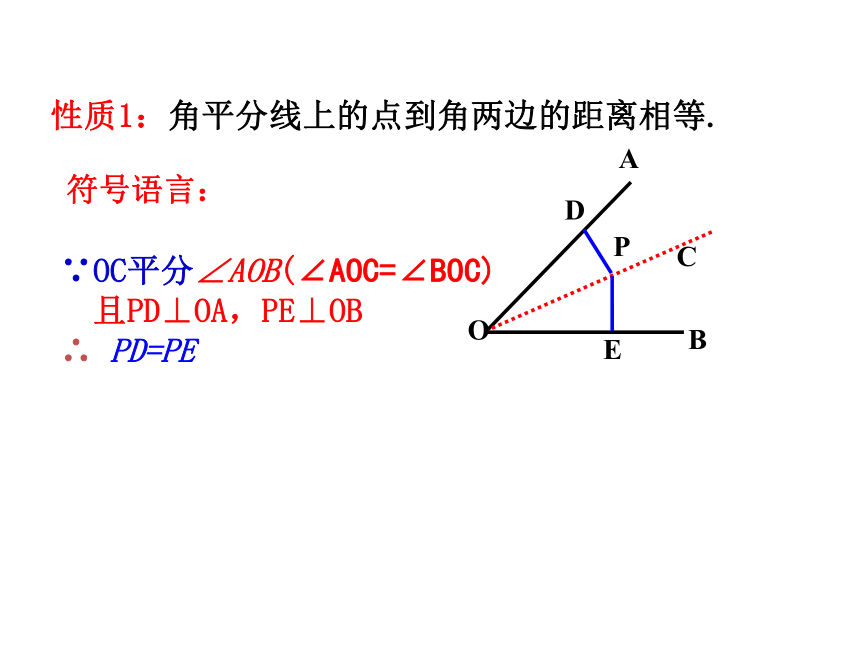
性质1:角平分线上的点到角两边的距离相等.
∵OC平分∠AOB(∠AOC=∠BOC)
且PD⊥OA,PE⊥OB
∴ PD=PE
符号语言:
在上面第二个结论中,有两个条件(1)OC是∠AOB的平分线;
(2)点P在OC上,PD⊥OA,PE⊥OB,才能得出PD=PE,两者缺一不可.下图中PD=PE吗?各缺少了什么条件?
问题3 角平分线的性质定理的逆命题是什么?
它成立吗?
追问1 你能画出图形吗?
追问2 根据前面的经验,你如何探究?
讨论:
如果一点在一个角的平分线上,那么这个点到这个角的两边距离相等;反过来,如果一个点到一个角的两边的距离相等,那么这个点在这个角的平分线上吗?
如图,点P在∠AOB内,且PD⊥OA,PE⊥OB,垂足分别为D、E,PD=PE。
O
D
P
A
E
B
证明:点P在∠AOB的平分线上。
角的内部到角两边距离相等的点在角的平分线上。
符号语言:
∵PD⊥OA,PE⊥OB,
且PD=PE
∴OP平分∠AOB.
角的内部到角两边距离相等的点在角的平分线上。
判定定理
O
D
E
A
B
P
C
例1、任意画∠O,在∠O的两边上分别截取OA、OB,使OA=OB,过点A画OA的垂线,过点B画OB的垂线,设2条垂线相交于点P,点O在∠APB的平分线上吗?为什么?
三、例题:
1、角是轴对称图形,它的角平分线是它的对称轴;
2、角平分线定理:
角平分线上的点到角两边的距离相等;
3、角平分线的逆定理:
角的内部到角两边距离相等的点
在角的平分线上。
四:课堂小结:
https://www.21cnjy.com/help/help_extract.php
苏科版 八年级上
苏科版八年级上册
2.4线段角的轴对称性(3)
1、使学生掌握角是轴对称图形,角平分线的性质.
2、使学生通过类比的思想和方法掌握本节课的内容,培养学生主动探索学习的能力
3、通过类比方法,掌握了新的知识,提高学生自学的兴趣和信心.
学习目标
如图两条高速公路在点O处交叉,点C点D为两个城镇,请你在该平面上选取一点P,使它到两条高速公路的距离相等,且到两个乡镇的距离也相等。
O
A
B
C
D
一、情境创设
1、请同学们将事先准备的薄纸拿出来,在上面任意画一个角
(∠AOB),折纸使两边OA、OB重合,你发现折痕与∠AOB
有什么关系?你有什么结论:
二. 自主探究
问题1 角是轴对称图形吗?对称轴是什么?
角是轴对称图形,角平分线所在的直线是它的对称轴.
2、在∠AOB的内部任意取折痕上的一点P,分别作点P到OA和OB的垂线段PD、PE,再沿原折痕折纸。你又有什么结论?
问题2 角平分线上的点有怎样的特殊性质?
追问1 在∠AOB的平分线上任意取一点P,分别画点P到OA和OB的垂线段PD和PE.PD与PE相等吗 为什么?
追问2 请同学们自主阅读教材54页,思考课本是如何说理的?
追问3 你还有什么方法证明这个结论?
性质1:角的平分线上的点到角的两边距离相等.
O
D
E
A
B
P
C
性质1:角平分线上的点到角两边的距离相等.
∵OC平分∠AOB(∠AOC=∠BOC)
且PD⊥OA,PE⊥OB
∴ PD=PE
符号语言:
在上面第二个结论中,有两个条件(1)OC是∠AOB的平分线;
(2)点P在OC上,PD⊥OA,PE⊥OB,才能得出PD=PE,两者缺一不可.下图中PD=PE吗?各缺少了什么条件?
问题3 角平分线的性质定理的逆命题是什么?
它成立吗?
追问1 你能画出图形吗?
追问2 根据前面的经验,你如何探究?
讨论:
如果一点在一个角的平分线上,那么这个点到这个角的两边距离相等;反过来,如果一个点到一个角的两边的距离相等,那么这个点在这个角的平分线上吗?
如图,点P在∠AOB内,且PD⊥OA,PE⊥OB,垂足分别为D、E,PD=PE。
O
D
P
A
E
B
证明:点P在∠AOB的平分线上。
角的内部到角两边距离相等的点在角的平分线上。
符号语言:
∵PD⊥OA,PE⊥OB,
且PD=PE
∴OP平分∠AOB.
角的内部到角两边距离相等的点在角的平分线上。
判定定理
O
D
E
A
B
P
C
例1、任意画∠O,在∠O的两边上分别截取OA、OB,使OA=OB,过点A画OA的垂线,过点B画OB的垂线,设2条垂线相交于点P,点O在∠APB的平分线上吗?为什么?
三、例题:
1、角是轴对称图形,它的角平分线是它的对称轴;
2、角平分线定理:
角平分线上的点到角两边的距离相等;
3、角平分线的逆定理:
角的内部到角两边距离相等的点
在角的平分线上。
四:课堂小结:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
