2021-2022学年高二上学期数学人教B版(2019)必修第四册9.2正弦定理与余弦定理的应用课件(共26张PPT)
文档属性
| 名称 | 2021-2022学年高二上学期数学人教B版(2019)必修第四册9.2正弦定理与余弦定理的应用课件(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-06 20:36:54 | ||
图片预览




文档简介
(共26张PPT)
9.2 正弦定理与余弦定理的应用
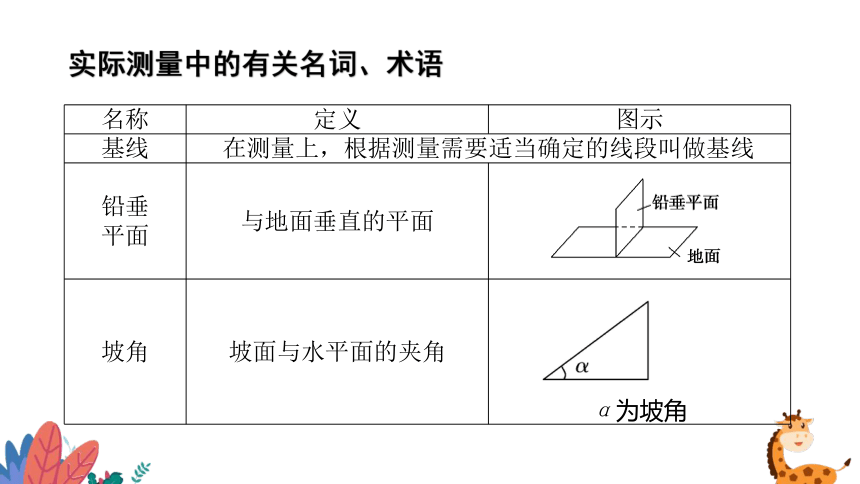
实际测量中的有关名词、术语
名称 定义 图示
基线 在测量上,根据测量需要适当确定的线段叫做基线 铅垂 平面 与地面垂直的平面
坡角 坡面与水平面的夹角
α为坡角
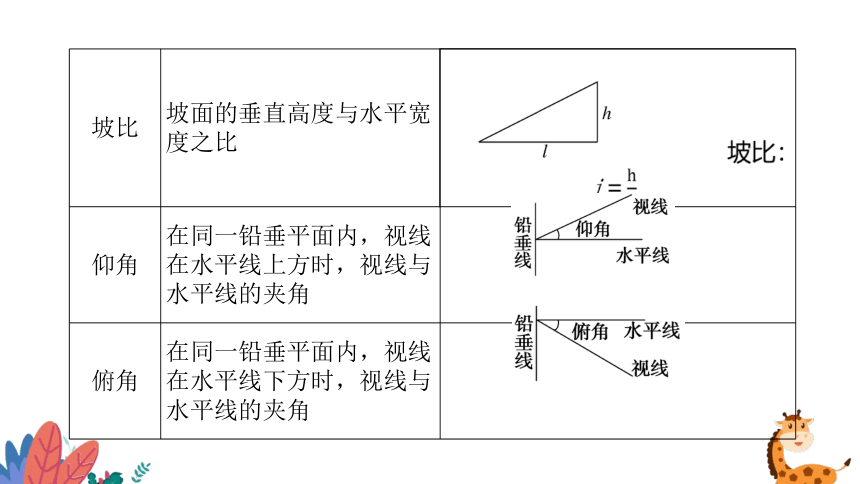
坡比 坡面的垂直高度与水平宽度之比
坡比:i=
仰角 在同一铅垂平面内,视线在水平线上方时,视线与水平线的夹角
俯角 在同一铅垂平面内,视线在水平线下方时,视线与水平线的夹角
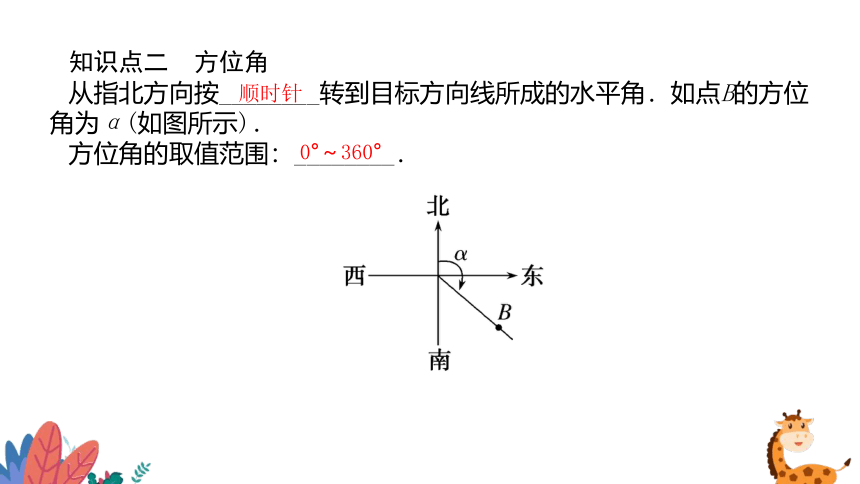
知识点二 方位角
从指北方向按________转到目标方向线所成的水平角.如点B的方位角为α(如图所示).
方位角的取值范围:________.
顺时针
0°~360°
知识点三 方向角
从指定方向线到目标方向线所成的小于________的水平角,如南偏西60°,指以________方向为始边,顺时针方向________旋转60°.
90°
正南
向西
[基础自测]
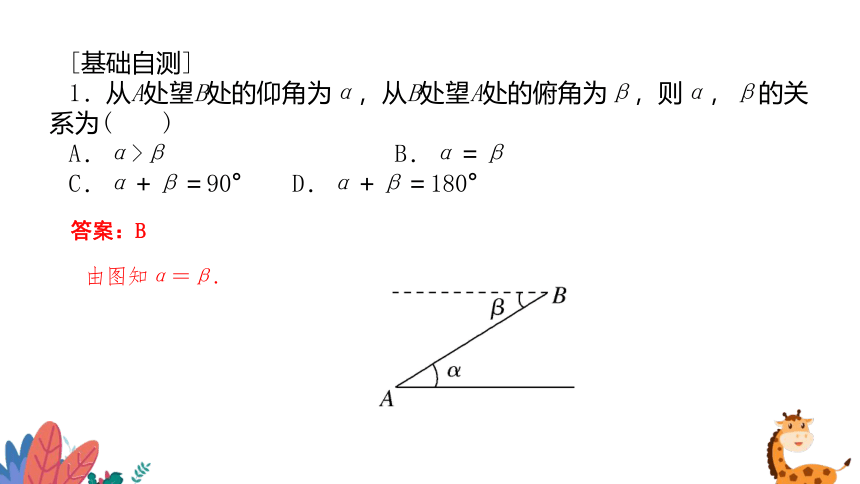
1.从A处望B处的仰角为α,从B处望A处的俯角为β,则α,β的关系为( )
A.α>β B.α=β
C.α+β=90° D.α+β=180°
由图知α=β.
答案:B
2.如图,已知两座灯塔A和B与海洋观察站C的距离都等于a km,灯塔A在观察站C的北偏东20°,灯塔B在观察站C的南偏东40°,则灯塔A与B的距离为( )
A.a km B.a km
C.a km D.2a km
在△ABC中,因为AC=BC=a,
∠ACB=180°-20°-40°=120°,
由余弦定理可得AB2=a2+a2-2a×a×cos 120°=3a2,所以AB=a,故选B.
答案:B
3.甲、乙两楼相距20 m,从乙楼底望甲楼顶的仰角为60°,从甲楼顶望乙楼顶的俯角为30°,则甲、乙两楼的高分别是________m、________m.
甲楼的高为:20tan 60°=20×=20(m);
乙楼的高为:20-20tan 30°=20-20×=(m).
20
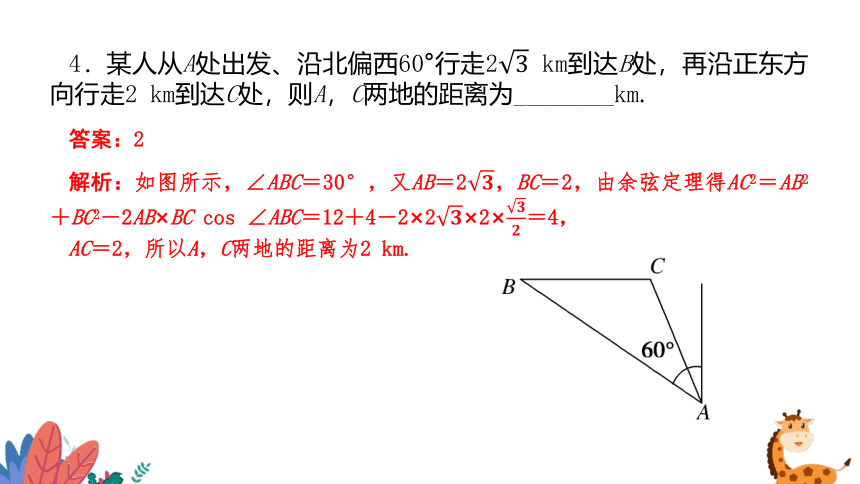
4.某人从A处出发、沿北偏西60°行走2 km到达B处,再沿正东方向行走2 km到达C处,则A,C两地的距离为________km.
解析:如图所示,∠ABC=30°,又AB=2,BC=2,由余弦定理得AC2=AB2+BC2-2AB×BC cos ∠ABC=12+4-2×2×2×=4,
AC=2,所以A,C两地的距离为2 km.
答案:2
测量不便到达的两点之间的距离问题
要测量对岸A,B两点之间的距离,选取相距 km的C,D两点,并测得∠ACB=75°,∠BCD=45°,∠ADC=30°,∠ADB=45°,求A,B之间的距离.
在△ACD中,∠ACD=120°,∠CAD=∠ADC=30°,
∴AC=CD= km.
在△BCD中,∠BCD=45°,
∠BDC=75°,∠CBD=60°.
∴BC==.
在△ABC中,由余弦定理,得
AB2=()2+-2××cos 75°
=3+2+=5,
∴AB=(km),∴A,B之间的距离为 km.
测量两个不可到达的点之间的距离,一般是把求距离问题转化为应用余弦定理求三角形的边长问题,然后把求未知的另外边长问题转化为只有一点不能到达的两点距离测量问题,运用正弦定理解决.
设B、C两点在河的两岸,要测量两点之间的距离,测量者在C的同侧,在所在的河岸边选定一点A,测出A,C的距离是100 m,∠BAC=45°,∠BCA=60°,求B,C两点间的距离.
在△ABC中,AC=100,∠BAC=45°,∠BCA=60°,
则∠B=180°-(∠BAC+∠BCA)=75°,
由正弦定理,得BC=AC×==100(-1).
即B,C两点间的距离为100(-1) m.
测量高度问题
某兴趣小组要测量电视塔AE的高度H(单位:m).如图所示,竖直放置的标杆BC的高度h=4 m,仰角∠ABE=α,∠ADE=β.该小组已测得一组α,β的值,算出了tan α=1.24,tan β=1.20,请据此算出H的值.
由AB=,BD=,
AD=及AB+BD=AD,
得=,
解得H===124.
因此,算出的电视塔的高度H是124 m.
如图所示,从山顶望地面上C,D两点,测得它们的俯角分别为45°和30°,已知CD=100 m,点C位于BD上,则山高AB等于( )
A.100 m B.50 m
C.50 m D.50(+1) m
设山高为h,则由题意知
CB=h,DB=h,
所以h-h=100,即h=50(+1).
答案:D
求航向的角度
某渔轮在航行中不幸遇险,发出呼救信号,我海军舰艇在A处获悉后,立即测出该渔轮在方位角为45°,距离为10 n mile的C处,并测得渔轮正沿方位角为105°的方向,以9 n mile/h 的速度向某小岛靠拢,我海军舰艇立即以21 n mile/h的速度前去营救,求舰艇的航向和靠近渔轮所需的时间.
可知AC=10,∠ACB=120°,设舰艇靠近渔轮所需的时间为t h,并在B处与渔轮相遇,则AB=21t,BC=9t,在△ABC中,根据余弦定理得AB2=AC2+BC2-2AC·BC·cos 120°,所以212t2=102+81t2+2×10×9t×,即360t2-90t-100=0,解得t=或t=-(舍去).所以舰艇靠近渔轮所需的时间为 h.
此时AB=14,BC=6.
在△ABC中,根据正弦定理得=,
所以sin ∠CAB==,
即∠CAB≈21.8°或∠CAB≈158.2°(舍去).
即舰艇航行的方位角为45°+21.8°=66.8°.
所以舰艇以66.8°的方位角航行,需 h才能靠近渔轮.
甲船在A处观察到乙船在它的北偏东60°方向的B处,两船相距a海里,乙船正向北行驶,若甲船的速度是乙船速度的倍,问甲船应沿什么方向前进才能在最短时间内追上乙船?此时乙船行驶了多少海里?
解析:设甲船沿直线AC与乙船同时到达C点,则A,B,C三点构成△ABC,如图.设乙船速度为v海里/时,则甲船速度为v海里/时,用时为t h.
由题意得BC=vt,AC=vt,∠ABC=120°.
∴3v2t2=a2+v2t2+avt,
∴2v2t2-avt-a2=0,解得vt=-(舍去)或vt=a,
∴BC=a海里.
在△ABC中,AB=BC=a海里,∴∠BAC=∠ACB=30°.
故甲船应沿北偏东30°的方向前进才能在最短时间内追上乙船,此时乙船行驶了a海里.
求解速度问题
1.某物流投递员沿一条大路前进,从A到B,方位角是50 °,距离是4 km,从B到C,方位角是80 °,距离是8 km,从C到D,方位角是150 °,距离是6 km,试画出示意图.
2.在探究1中,若投递员想在半小时之内,沿小路直接从A点到C,则此人的速度至少是多少?
在△ABC中,∠ABC =50 °+(180 °-80 °) =150 °,由余弦定理得AC = =,则此人的最小速度为v = =8(km/h).
3.在探究1中若投递员以24 km/h的速度匀速沿大路从A到D前进,10分钟后某人以16 km/h的速度沿小路直接由A到C追投递员,问在C点此人能否与投递员相遇?
投递员到达C点的时间为t1 = =(小时) =30(分钟),追投递员的人所用时间由探究2可知t2 =≈0. 55 小时 =33分钟;由于30<33+10,所以此人在C点不能与投递员相遇.
例4 如图所示,一辆汽车从O点出发沿一条直线公路以50公里/小时的速度匀速行驶(图中的箭头方向为汽车行驶方向),汽车开动的同时,在距汽车出发点O点的距离为5公里、距离公路线的垂直距离为3公里的M点的地方有一个人骑摩托车出发想把一件东西送给汽车司机.问骑摩托车的人至少以多大的速度匀速行驶才能实现他的愿望,此时他驾驶摩托车行驶了多少公里?
【解析】 作MI垂直公路所在直线于点I,则MI=3,∵OM=5,∴OI=4,
∴cos ∠MOI=.
设骑摩托车的人的速度为v公里/小时,追上汽车的时间为t小时,
由余弦定理得(vt)2=52+(50t)2-2×5×50t×,
即v2=+2 500=25+900≥900,
∴当t=时,v取得最小值为30,
∴其行驶距离为vt==(公里).
故骑摩托车的人至少以30公里/小时的速度行驶才能实现他的愿望,此时他驾驶摩托车行驶了公里.
一艘船上午9:30在A处测得灯塔S在它的北偏东30°的方向上,且与它相距8海里,之后它继续沿正北方向匀速航行,上午10:00到达B处,此时测得灯塔S在它的北偏东75°的方向,则此船的航行速度为( )
A.8()海里/时 B.8()海里/时
C.16()海里/时 D.16()海里/时
答案:D
解析:在△SAB中,∠BAS=30°,∠SBA=180°-75°=105°,∠BSA=45°.
由正弦定理得=,
即=,得AB=8()海里,
因此该船的航行速度为=16(
)(海里/时).
9.2 正弦定理与余弦定理的应用
实际测量中的有关名词、术语
名称 定义 图示
基线 在测量上,根据测量需要适当确定的线段叫做基线 铅垂 平面 与地面垂直的平面
坡角 坡面与水平面的夹角
α为坡角
坡比 坡面的垂直高度与水平宽度之比
坡比:i=
仰角 在同一铅垂平面内,视线在水平线上方时,视线与水平线的夹角
俯角 在同一铅垂平面内,视线在水平线下方时,视线与水平线的夹角
知识点二 方位角
从指北方向按________转到目标方向线所成的水平角.如点B的方位角为α(如图所示).
方位角的取值范围:________.
顺时针
0°~360°
知识点三 方向角
从指定方向线到目标方向线所成的小于________的水平角,如南偏西60°,指以________方向为始边,顺时针方向________旋转60°.
90°
正南
向西
[基础自测]
1.从A处望B处的仰角为α,从B处望A处的俯角为β,则α,β的关系为( )
A.α>β B.α=β
C.α+β=90° D.α+β=180°
由图知α=β.
答案:B
2.如图,已知两座灯塔A和B与海洋观察站C的距离都等于a km,灯塔A在观察站C的北偏东20°,灯塔B在观察站C的南偏东40°,则灯塔A与B的距离为( )
A.a km B.a km
C.a km D.2a km
在△ABC中,因为AC=BC=a,
∠ACB=180°-20°-40°=120°,
由余弦定理可得AB2=a2+a2-2a×a×cos 120°=3a2,所以AB=a,故选B.
答案:B
3.甲、乙两楼相距20 m,从乙楼底望甲楼顶的仰角为60°,从甲楼顶望乙楼顶的俯角为30°,则甲、乙两楼的高分别是________m、________m.
甲楼的高为:20tan 60°=20×=20(m);
乙楼的高为:20-20tan 30°=20-20×=(m).
20
4.某人从A处出发、沿北偏西60°行走2 km到达B处,再沿正东方向行走2 km到达C处,则A,C两地的距离为________km.
解析:如图所示,∠ABC=30°,又AB=2,BC=2,由余弦定理得AC2=AB2+BC2-2AB×BC cos ∠ABC=12+4-2×2×2×=4,
AC=2,所以A,C两地的距离为2 km.
答案:2
测量不便到达的两点之间的距离问题
要测量对岸A,B两点之间的距离,选取相距 km的C,D两点,并测得∠ACB=75°,∠BCD=45°,∠ADC=30°,∠ADB=45°,求A,B之间的距离.
在△ACD中,∠ACD=120°,∠CAD=∠ADC=30°,
∴AC=CD= km.
在△BCD中,∠BCD=45°,
∠BDC=75°,∠CBD=60°.
∴BC==.
在△ABC中,由余弦定理,得
AB2=()2+-2××cos 75°
=3+2+=5,
∴AB=(km),∴A,B之间的距离为 km.
测量两个不可到达的点之间的距离,一般是把求距离问题转化为应用余弦定理求三角形的边长问题,然后把求未知的另外边长问题转化为只有一点不能到达的两点距离测量问题,运用正弦定理解决.
设B、C两点在河的两岸,要测量两点之间的距离,测量者在C的同侧,在所在的河岸边选定一点A,测出A,C的距离是100 m,∠BAC=45°,∠BCA=60°,求B,C两点间的距离.
在△ABC中,AC=100,∠BAC=45°,∠BCA=60°,
则∠B=180°-(∠BAC+∠BCA)=75°,
由正弦定理,得BC=AC×==100(-1).
即B,C两点间的距离为100(-1) m.
测量高度问题
某兴趣小组要测量电视塔AE的高度H(单位:m).如图所示,竖直放置的标杆BC的高度h=4 m,仰角∠ABE=α,∠ADE=β.该小组已测得一组α,β的值,算出了tan α=1.24,tan β=1.20,请据此算出H的值.
由AB=,BD=,
AD=及AB+BD=AD,
得=,
解得H===124.
因此,算出的电视塔的高度H是124 m.
如图所示,从山顶望地面上C,D两点,测得它们的俯角分别为45°和30°,已知CD=100 m,点C位于BD上,则山高AB等于( )
A.100 m B.50 m
C.50 m D.50(+1) m
设山高为h,则由题意知
CB=h,DB=h,
所以h-h=100,即h=50(+1).
答案:D
求航向的角度
某渔轮在航行中不幸遇险,发出呼救信号,我海军舰艇在A处获悉后,立即测出该渔轮在方位角为45°,距离为10 n mile的C处,并测得渔轮正沿方位角为105°的方向,以9 n mile/h 的速度向某小岛靠拢,我海军舰艇立即以21 n mile/h的速度前去营救,求舰艇的航向和靠近渔轮所需的时间.
可知AC=10,∠ACB=120°,设舰艇靠近渔轮所需的时间为t h,并在B处与渔轮相遇,则AB=21t,BC=9t,在△ABC中,根据余弦定理得AB2=AC2+BC2-2AC·BC·cos 120°,所以212t2=102+81t2+2×10×9t×,即360t2-90t-100=0,解得t=或t=-(舍去).所以舰艇靠近渔轮所需的时间为 h.
此时AB=14,BC=6.
在△ABC中,根据正弦定理得=,
所以sin ∠CAB==,
即∠CAB≈21.8°或∠CAB≈158.2°(舍去).
即舰艇航行的方位角为45°+21.8°=66.8°.
所以舰艇以66.8°的方位角航行,需 h才能靠近渔轮.
甲船在A处观察到乙船在它的北偏东60°方向的B处,两船相距a海里,乙船正向北行驶,若甲船的速度是乙船速度的倍,问甲船应沿什么方向前进才能在最短时间内追上乙船?此时乙船行驶了多少海里?
解析:设甲船沿直线AC与乙船同时到达C点,则A,B,C三点构成△ABC,如图.设乙船速度为v海里/时,则甲船速度为v海里/时,用时为t h.
由题意得BC=vt,AC=vt,∠ABC=120°.
∴3v2t2=a2+v2t2+avt,
∴2v2t2-avt-a2=0,解得vt=-(舍去)或vt=a,
∴BC=a海里.
在△ABC中,AB=BC=a海里,∴∠BAC=∠ACB=30°.
故甲船应沿北偏东30°的方向前进才能在最短时间内追上乙船,此时乙船行驶了a海里.
求解速度问题
1.某物流投递员沿一条大路前进,从A到B,方位角是50 °,距离是4 km,从B到C,方位角是80 °,距离是8 km,从C到D,方位角是150 °,距离是6 km,试画出示意图.
2.在探究1中,若投递员想在半小时之内,沿小路直接从A点到C,则此人的速度至少是多少?
在△ABC中,∠ABC =50 °+(180 °-80 °) =150 °,由余弦定理得AC = =,则此人的最小速度为v = =8(km/h).
3.在探究1中若投递员以24 km/h的速度匀速沿大路从A到D前进,10分钟后某人以16 km/h的速度沿小路直接由A到C追投递员,问在C点此人能否与投递员相遇?
投递员到达C点的时间为t1 = =(小时) =30(分钟),追投递员的人所用时间由探究2可知t2 =≈0. 55 小时 =33分钟;由于30<33+10,所以此人在C点不能与投递员相遇.
例4 如图所示,一辆汽车从O点出发沿一条直线公路以50公里/小时的速度匀速行驶(图中的箭头方向为汽车行驶方向),汽车开动的同时,在距汽车出发点O点的距离为5公里、距离公路线的垂直距离为3公里的M点的地方有一个人骑摩托车出发想把一件东西送给汽车司机.问骑摩托车的人至少以多大的速度匀速行驶才能实现他的愿望,此时他驾驶摩托车行驶了多少公里?
【解析】 作MI垂直公路所在直线于点I,则MI=3,∵OM=5,∴OI=4,
∴cos ∠MOI=.
设骑摩托车的人的速度为v公里/小时,追上汽车的时间为t小时,
由余弦定理得(vt)2=52+(50t)2-2×5×50t×,
即v2=+2 500=25+900≥900,
∴当t=时,v取得最小值为30,
∴其行驶距离为vt==(公里).
故骑摩托车的人至少以30公里/小时的速度行驶才能实现他的愿望,此时他驾驶摩托车行驶了公里.
一艘船上午9:30在A处测得灯塔S在它的北偏东30°的方向上,且与它相距8海里,之后它继续沿正北方向匀速航行,上午10:00到达B处,此时测得灯塔S在它的北偏东75°的方向,则此船的航行速度为( )
A.8()海里/时 B.8()海里/时
C.16()海里/时 D.16()海里/时
答案:D
解析:在△SAB中,∠BAS=30°,∠SBA=180°-75°=105°,∠BSA=45°.
由正弦定理得=,
即=,得AB=8()海里,
因此该船的航行速度为=16(
)(海里/时).
