1.3 探索三角形全等的条件(6) 课件(共14张PPT)
文档属性
| 名称 | 1.3 探索三角形全等的条件(6) 课件(共14张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-05 20:39:29 | ||
图片预览




文档简介
(共14张PPT)
苏科版 八年级上
初中数学
1.3 探索三角形全等的条件(6)
用直尺和圆规作△ABC,使AB=c,AC=b,BC=a.
a
b
c
步骤:
1.作线段AB=c.
2.分别以点A、B为圆心,
b、a的长为半径画弧,
两弧相交于点C .
3.连结AC、BC.
a
b
c
A
B
C
△ABC就是所求作的三角形.
你作的三角形与其他同学作的三角形能完全重合吗?
一、自主探究
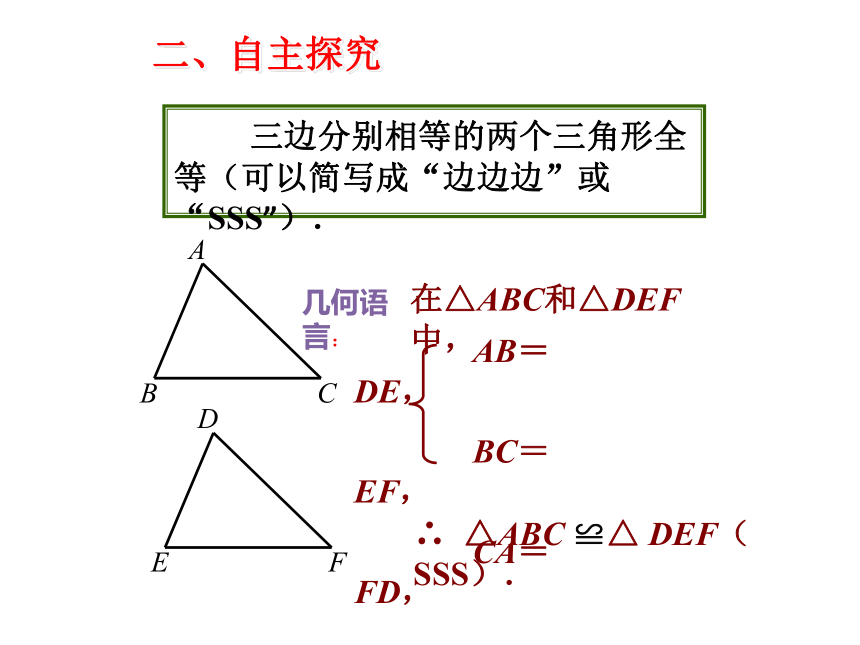
三边分别相等的两个三角形全等(可以简写成“边边边”或“SSS”).
A
B
C
D
E
F
在△ABC和△DEF中,
∴ △ABC ≌△ DEF(SSS).
AB=DE,
BC=EF,
CA=FD,
二、自主探究
几何语言:
如果一个三角形三边的长度确定,那么这个三角形的形状和大小就完全确定.三角形的这个性质叫做三角形的稳定性.
二、自主探究
四边形具有稳定性吗?
①
②
③
④
⑤
⑥
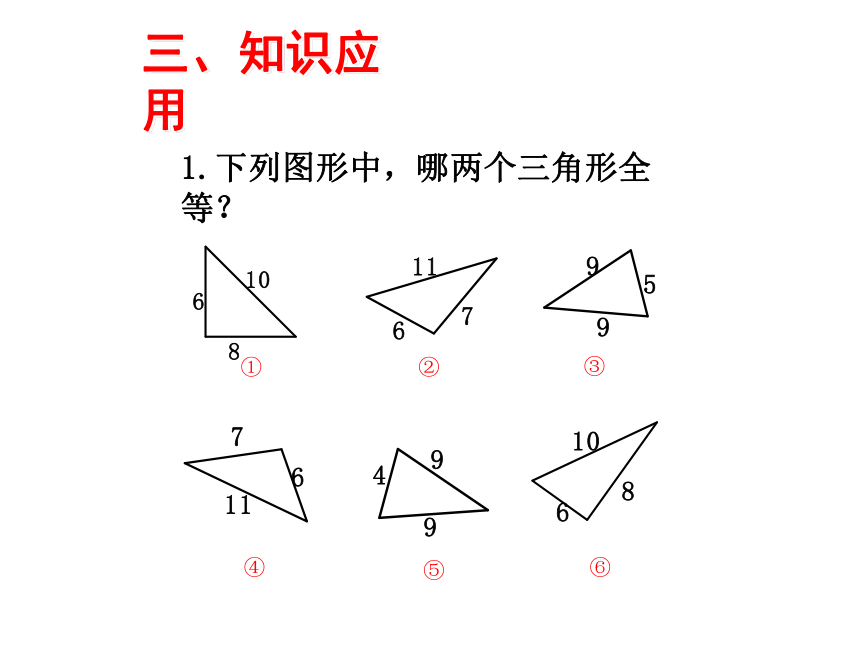
1.下列图形中,哪两个三角形全等?
三、知识应用
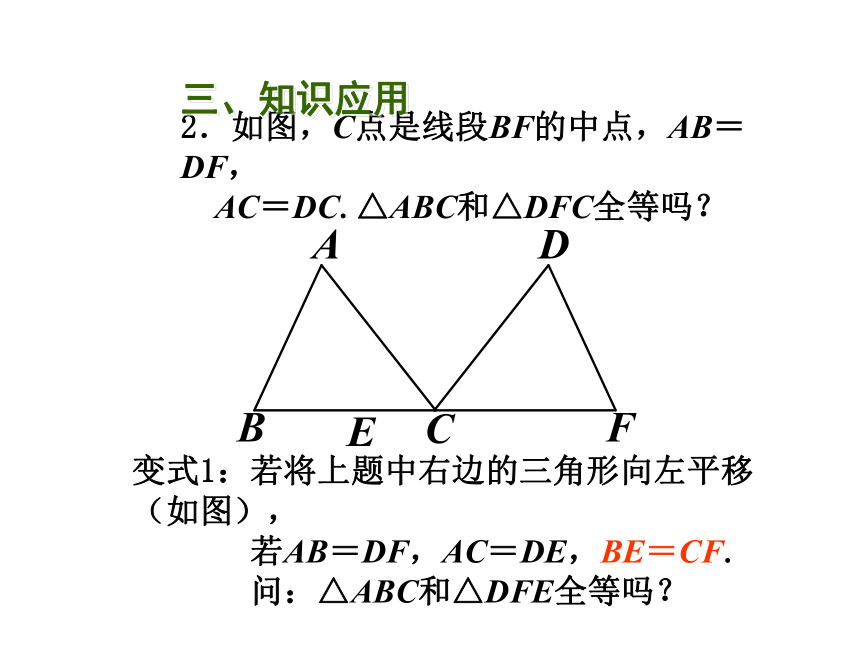
变式1:若将上题中右边的三角形向左平移(如图),
若AB=DF,AC=DE,BE=CF.
问:△ABC和△DFE全等吗?
2.如图,C点是线段BF的中点,AB=DF,
AC=DC.△ABC和△DFC全等吗?
B
A
C
E
F
D
三、知识应用
变式2:若将上题中的三角形继续向左平移(如图),
若AB=DC,AC=DB,
问:△ABC≌△DCB 吗?
B
A
C
E
F
D
三、知识应用
2.如图,C点是线段BF的中点,AB=DF,
AC=DC.△ABC和△DFC全等吗?
3.已知:如图, 在△ABC 中,AB=AC,
求证:∠B=∠C.
D
在△ABD和△ACD中,
∴ △ABD ≌△ ACD(SSS).
AB=AC(已知),
BD=CD(辅助线作法),
AD=AD(公共边),
证明:作△ABC 的中线AD.
∴ ∠B=∠C (全等三角形的对应角相等).
三、知识应用
五、课堂小结
通过这节课的学习与探索,你有哪些收获?
1.已知:如图,AB=CD,AD=CB,
求证:∠B=∠D.
A
B
C
D
证明:连结AC,
在△ABC 和△CDA中,
AB=CD(已知),
BC=DA(已知),
AC=CA(公共边),
∴ △ABC≌△CDA(SSS),
∴∠B=∠D .
当堂检测
2.如图,AC、BD相交于点O,且AB=DC,
AC=BD.求证:∠A=∠D.
当堂检测
变式:求证:∠B=∠C.
https://www.21cnjy.com/help/help_extract.php
苏科版 八年级上
初中数学
1.3 探索三角形全等的条件(6)
用直尺和圆规作△ABC,使AB=c,AC=b,BC=a.
a
b
c
步骤:
1.作线段AB=c.
2.分别以点A、B为圆心,
b、a的长为半径画弧,
两弧相交于点C .
3.连结AC、BC.
a
b
c
A
B
C
△ABC就是所求作的三角形.
你作的三角形与其他同学作的三角形能完全重合吗?
一、自主探究
三边分别相等的两个三角形全等(可以简写成“边边边”或“SSS”).
A
B
C
D
E
F
在△ABC和△DEF中,
∴ △ABC ≌△ DEF(SSS).
AB=DE,
BC=EF,
CA=FD,
二、自主探究
几何语言:
如果一个三角形三边的长度确定,那么这个三角形的形状和大小就完全确定.三角形的这个性质叫做三角形的稳定性.
二、自主探究
四边形具有稳定性吗?
①
②
③
④
⑤
⑥
1.下列图形中,哪两个三角形全等?
三、知识应用
变式1:若将上题中右边的三角形向左平移(如图),
若AB=DF,AC=DE,BE=CF.
问:△ABC和△DFE全等吗?
2.如图,C点是线段BF的中点,AB=DF,
AC=DC.△ABC和△DFC全等吗?
B
A
C
E
F
D
三、知识应用
变式2:若将上题中的三角形继续向左平移(如图),
若AB=DC,AC=DB,
问:△ABC≌△DCB 吗?
B
A
C
E
F
D
三、知识应用
2.如图,C点是线段BF的中点,AB=DF,
AC=DC.△ABC和△DFC全等吗?
3.已知:如图, 在△ABC 中,AB=AC,
求证:∠B=∠C.
D
在△ABD和△ACD中,
∴ △ABD ≌△ ACD(SSS).
AB=AC(已知),
BD=CD(辅助线作法),
AD=AD(公共边),
证明:作△ABC 的中线AD.
∴ ∠B=∠C (全等三角形的对应角相等).
三、知识应用
五、课堂小结
通过这节课的学习与探索,你有哪些收获?
1.已知:如图,AB=CD,AD=CB,
求证:∠B=∠D.
A
B
C
D
证明:连结AC,
在△ABC 和△CDA中,
AB=CD(已知),
BC=DA(已知),
AC=CA(公共边),
∴ △ABC≌△CDA(SSS),
∴∠B=∠D .
当堂检测
2.如图,AC、BD相交于点O,且AB=DC,
AC=BD.求证:∠A=∠D.
当堂检测
变式:求证:∠B=∠C.
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
