1.3 探索三角形全等的条件(7) 课件(共13张PPT)
文档属性
| 名称 | 1.3 探索三角形全等的条件(7) 课件(共13张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-05 00:00:00 | ||
图片预览



文档简介
(共13张PPT)
谢 谢!
1.3 探索三角形全等的条件(7)
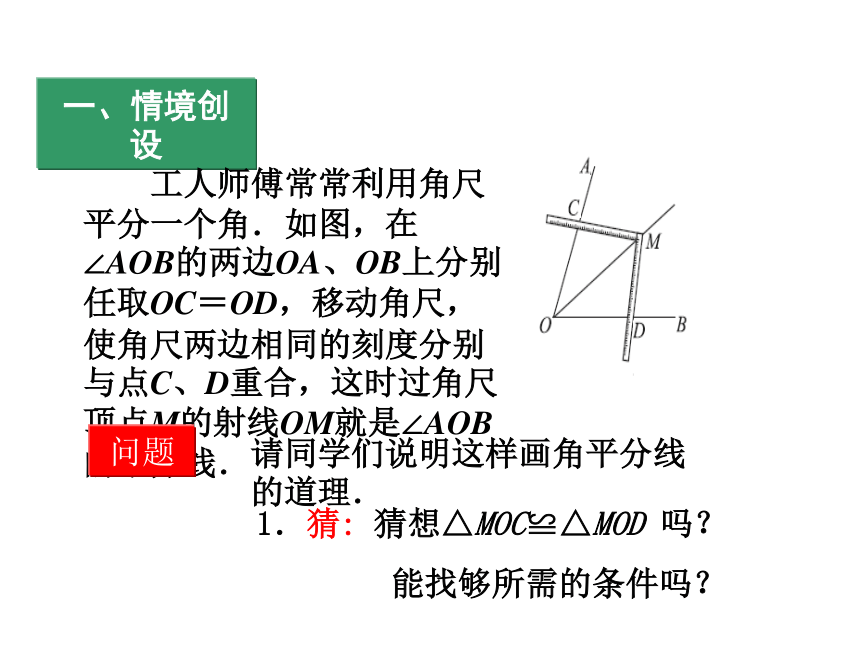
1.猜: 猜想△MOC≌△MOD 吗?
能找够所需的条件吗?
一、情境创设
工人师傅常常利用角尺平分一个角.如图,在∠AOB的两边OA、OB上分别任取OC=OD,移动角尺,使角尺两边相同的刻度分别与点C、D重合,这时过角尺顶点M的射线OM就是∠AOB的平分线.
问题
请同学们说明这样画角平分线的道理.
2.证: 证明你的猜想.
证明:在△MOC和△MOD中,
∴△MOC≌△MOD(SSS),
∴∠COM=∠DOM,
即OM平分∠AOB.
OC=OD,
OM=OM,
CM=DM,
3. 化: 将OC=OD、CM=DM转化为绘图语言,应如何表达?请拿出圆规尝试一下!
二、探索活动1
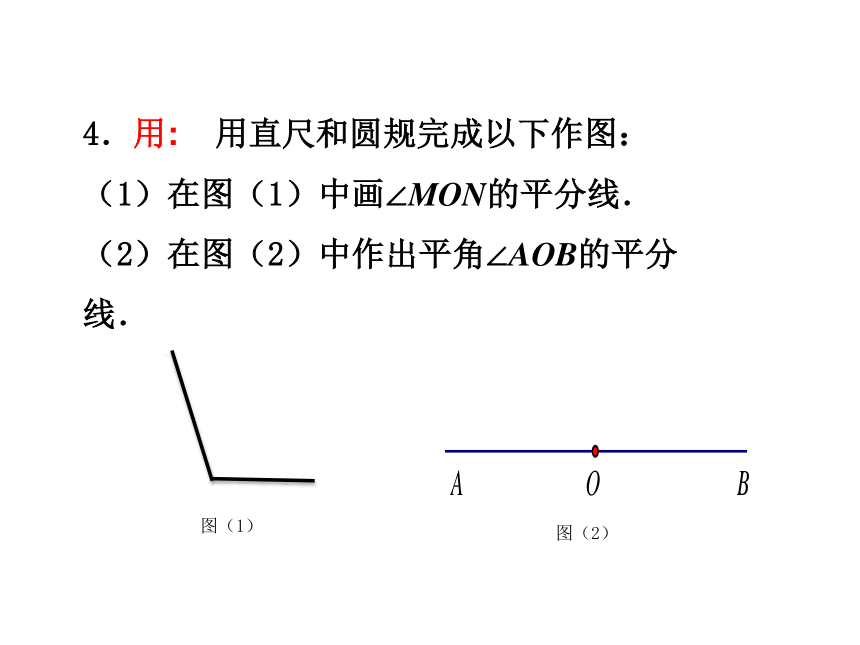
4.用: 用直尺和圆规完成以下作图:
(1)在图(1)中画∠MON的平分线.
(2)在图(2)中作出平角∠AOB的平分线.
图(1)
M
O
N
图(2)
三、探索活动2
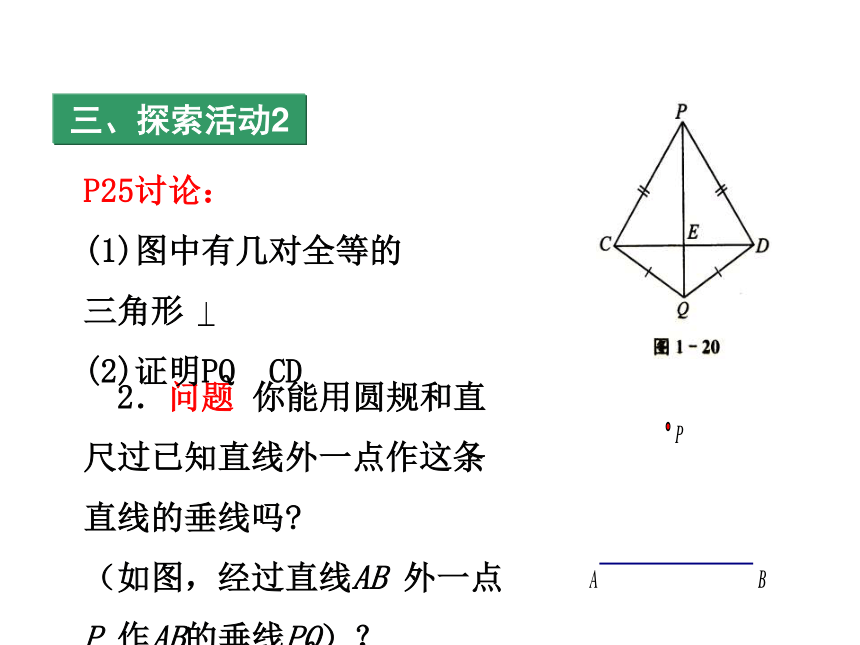
2.问题 你能用圆规和直尺过已知直线外一点作这条直线的垂线吗
(如图,经过直线AB 外一点P 作AB的垂线PQ)?
P25讨论:
(1)图中有几对全等的三角形
(2)证明PQ CD
3.提取—转化
4.总结作法.
提取已知“讨论”中的已知信息,转化成绘图语言
C
D
Q
·P
A
B
5.归纳总结.
经过一点可用直尺和圆规作一条直线与已知直线垂直.
四、知识运用
用直尺和圆规作一个直角三角形,使它的两条直角边分别等于a、b.
五、拓展延伸
如图,已知A、B是l上的两点,P是l外的一点.
(1)按照下面画法作图(保留作图痕迹):
①以A为圆心,AP为半径画弧;
②以B为圆心,BP为半径画弧;
③设两弧交于点Q(Q与P分别在l的两旁);
④连结PQ.
(2)求证:PQ⊥l.
六、课堂小结
作已知角的角平分线
过直线上的一点作已知直线的垂线
过直线外的一点作已知直线的垂线
特例
变式
方法1:活动二
方法2:拓展延伸
作法
过平面上一点作已知直线的垂线
作图依据:SSS
活动一
活动
二
知识应用:一题多解
七、课后作业
已知:∠AOB(如图)
求作:(1)∠AOB的平分线OC;
(2)作射线OD⊥OC(两种作法)
(3)在OC上取一点P,作出点P到∠AOB两边的垂线段,并比较这两条垂线段的大小关系
(要求保留作图痕迹,不写作法和证明过程) .
https://www.21cnjy.com/help/help_extract.php
谢 谢!
1.3 探索三角形全等的条件(7)
1.猜: 猜想△MOC≌△MOD 吗?
能找够所需的条件吗?
一、情境创设
工人师傅常常利用角尺平分一个角.如图,在∠AOB的两边OA、OB上分别任取OC=OD,移动角尺,使角尺两边相同的刻度分别与点C、D重合,这时过角尺顶点M的射线OM就是∠AOB的平分线.
问题
请同学们说明这样画角平分线的道理.
2.证: 证明你的猜想.
证明:在△MOC和△MOD中,
∴△MOC≌△MOD(SSS),
∴∠COM=∠DOM,
即OM平分∠AOB.
OC=OD,
OM=OM,
CM=DM,
3. 化: 将OC=OD、CM=DM转化为绘图语言,应如何表达?请拿出圆规尝试一下!
二、探索活动1
4.用: 用直尺和圆规完成以下作图:
(1)在图(1)中画∠MON的平分线.
(2)在图(2)中作出平角∠AOB的平分线.
图(1)
M
O
N
图(2)
三、探索活动2
2.问题 你能用圆规和直尺过已知直线外一点作这条直线的垂线吗
(如图,经过直线AB 外一点P 作AB的垂线PQ)?
P25讨论:
(1)图中有几对全等的三角形
(2)证明PQ CD
3.提取—转化
4.总结作法.
提取已知“讨论”中的已知信息,转化成绘图语言
C
D
Q
·P
A
B
5.归纳总结.
经过一点可用直尺和圆规作一条直线与已知直线垂直.
四、知识运用
用直尺和圆规作一个直角三角形,使它的两条直角边分别等于a、b.
五、拓展延伸
如图,已知A、B是l上的两点,P是l外的一点.
(1)按照下面画法作图(保留作图痕迹):
①以A为圆心,AP为半径画弧;
②以B为圆心,BP为半径画弧;
③设两弧交于点Q(Q与P分别在l的两旁);
④连结PQ.
(2)求证:PQ⊥l.
六、课堂小结
作已知角的角平分线
过直线上的一点作已知直线的垂线
过直线外的一点作已知直线的垂线
特例
变式
方法1:活动二
方法2:拓展延伸
作法
过平面上一点作已知直线的垂线
作图依据:SSS
活动一
活动
二
知识应用:一题多解
七、课后作业
已知:∠AOB(如图)
求作:(1)∠AOB的平分线OC;
(2)作射线OD⊥OC(两种作法)
(3)在OC上取一点P,作出点P到∠AOB两边的垂线段,并比较这两条垂线段的大小关系
(要求保留作图痕迹,不写作法和证明过程) .
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
